一种线性代数方程组新解法研究

李宛霖 姜伟琦

摘要：经典高斯消元法求解线性代数方程组用途广泛，但计算量巨大。本文研究LU分解法求解线性方程组，通过计算量分析说明LU分解法相对于传统解法的计算优势。

关键词：线性代数方程组;高斯消元法;LU分解法;线性方程组

1研究意义

在学习线性代数课程中对于线性代数方程组的求解是对为核心的内容，通过学习线性代数方程组为解决实际问题奠定了基础，也提供了学习方法。线性代数方程组应用在多个方面，在数学理论学习过程中尤其是在几何、代数等方面应用较广;在生活中线性代数方程组也运用非常广泛，例如在计算机、经济、化学、物理及航空等领域，像在我们所学习的课程中如，电路、力学、数字处理等课程也相继的使用。线性代數方程组应用的广泛带给我们对它求解方法也更为拓展，高斯消元法就是传统解法之一且使用率极高，但在使用过程中我们发现其中的不足，为了以后能更好的运用线性代数方程组，更好的求解，通过学习与探索，结合实际问题，适当掌握更好更优的解法，从而能够达到更有效更便捷的方式来解决实际问题作为目的。

结束语：

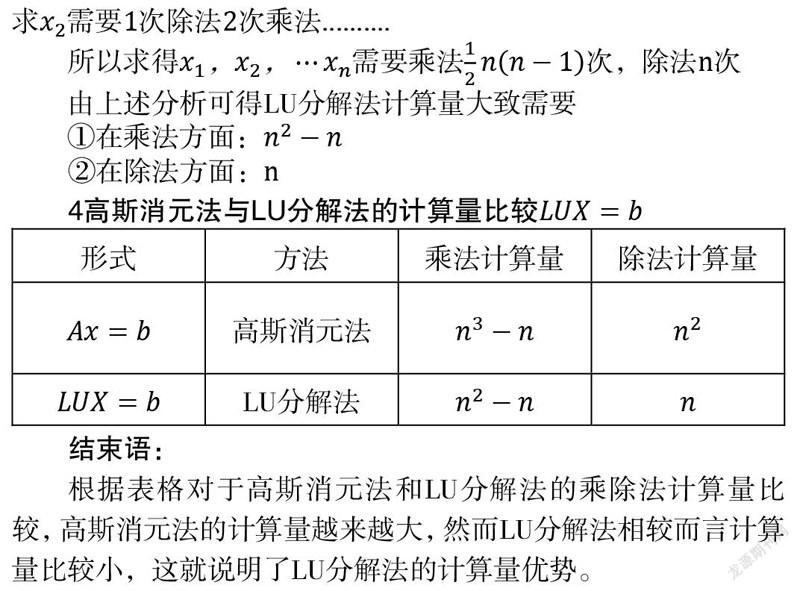
根据表格对于高斯消元法和LU分解法的乘除法计算量比较，高斯消元法的计算量越来越大，然而LU分解法相较而言计算量比较小，这就说明了LU分解法的计算量优势。

参考文献：

[1]李庆扬，王能超，易大义.数值分析（第5版）[M].北京：清华大学出版社，2008：142-162.

[2]康玉洁，王亚子，王朝君.线性方程组的数值解法比较与分析[J].周口师范学院学报，2017，34（2）：36-42.

[3]王艳天.解线性方程组的LU分解法[J].科技创新导报，2009，000（004）：245.

资助项目：本论文由北京物资学院大学生创新创业项目资助。

作者简介：

李宛霖，2002年2月20日，女，汉族，北京市石景山区，本科，北京物资学院在读本科生，研究方向：物联网工程。

姜伟琦，2002年2月8日，男，汉族，北京市大兴区，本科，北京物资学院在读本科生，研究方向：大数据管理与应用。