火灾后双钢板-混凝土组合剪力墙抗震性能有限元分析

徐庆鹏，韦芳芳，郑泽军，陈道申

(河海大学 土木与交通学院，江苏 南京 210098)

双钢板-混凝土组合剪力墙(Concrete-Filled Double Steel Plate Composite Shear Wall, CFDSPC)是在钢板中间内填混凝土，并通过栓钉等连接件紧密连接两者的新型抗侧力构件。目前，CFDSPC剪力墙在高层建筑[1-2]、核电站[3-5]等工程中得到广泛的利用，在各类建筑结构工程中具有良好的应用前景。全球范围内，不少高层建筑在施工、使用阶段曾遭受过火灾。如果火灾及时被扑灭，多数建筑在适当修复后可继续使用。CFDPSC剪力墙外侧钢板在火灾中易受到损害，但内填的混凝土可以吸收大量热量，提高钢-混凝土结构的耐火性能[6]。截至目前，CFDSPC剪力墙的火灾试验和火灾后抗震性能研究还较少。韦芳芳等[7]通过对3个CFDSPC剪力墙的单面火灾试验，研究了不同连接件形式对墙体耐火性能的影响。Wei等[8]对12个CFDSPC剪力墙进行了火灾试验，研究了受火方式、轴压比对其抗震性能的影响。国内外学者对CFDSPC剪力墙火灾后抗震性能研究较少。丁东升[9]完成了3榀CFDSPC剪力墙火灾后的拟静力试验，主要研究参数为剪跨比。在丁东升[9]的基础上，沈鹏程[10]完成了3榀常温下不同剪跨比的CFDSPC剪力墙拟静力试验。

综上所述，目前无法通过现有资料对CFDSPC剪力墙火灾后的力学性能进行评估，因此有必要深入研究CFDSPC剪力墙在火灾全过程中的力学性能。本文利用ABAQUS建立并验证了常温下和火灾后钢材和混凝土的本构模型以及建模方法的可靠性。基于相同建模方法，建立足尺的 CFDSPC剪力墙模型，对模型进行参数分析，如火灾时间、轴压比、剪跨比和混凝土抗压强度等，确定主要参数及其影响规律。

1 模型验证

1.1 温度场模型

CFDSPC剪力墙钢材和混凝土热工参数采用了Lie[11]给出的热工模型，考虑钢板外的热对流和热辐射，取综合热辐射率为0.56[12]，取受火面和背火面钢板的热对流系数分别为25 W/(m2·℃)[12]、9 W/(m2·℃)，钢-混凝土的界面热阻参照Lu等[13]有限元模拟试算结果，取接触导热系数为100 W/(m2·℃)，图1展示了CFDSPC剪力墙截面的热量传递过程。混凝土采用DC3D8实体热分析单元，钢管和钢板采用DS4热分析壳单元，所有钢筋(包括墙内钢筋和梁内钢筋)和墙内栓钉均采用DC1D2传热连接单元。钢板与混凝土梁、钢管与混凝土梁、栓钉与钢板均采用共节点连接；钢板与墙内混凝土、钢板与墙内混凝土均采用相互作用(Interaction)约束；所有钢筋与混凝土、栓钉与混凝土均采用绑定(Tie)约束。

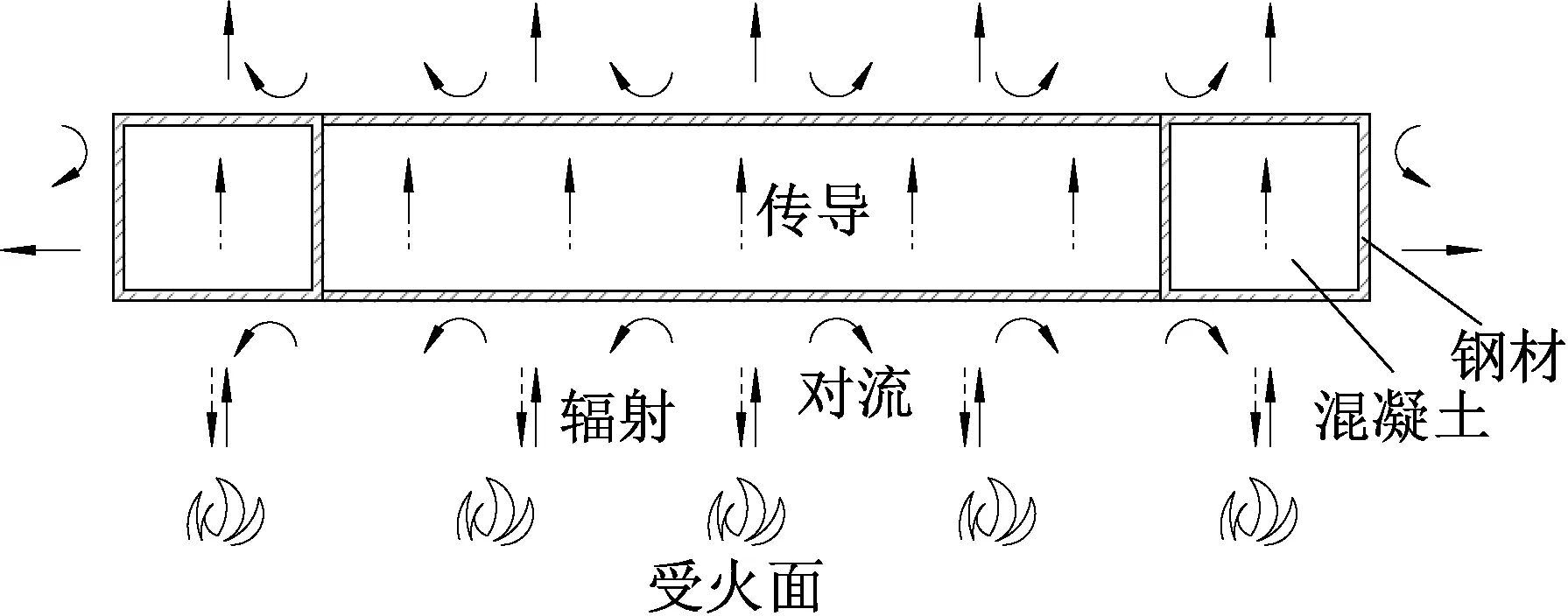
图1 CFDSPC剪力墙截面的热量传递图Fig.1 Heat Transfer Diagram of CFDSPC Shear Wall Section

1.2 常温下CFDSPC剪力墙试件的力学模型验证

1.2.1 模型的建立与验证

对聂建国[14-15]报道的8片栓钉连接的CFDSPC剪力墙拟静力试验进行模拟，所有试件均未经历过火灾。

CFDSPC剪力墙的抗震分析有限元模型，混凝土采用C3D8R实体单元，钢管和钢板采用S4R壳单元，钢筋和栓钉采用B31梁单元。钢板与混凝土梁、钢管与混凝土梁、栓钉与钢板均采用共节点连接；钢板与墙内混凝土、钢板与墙内混凝土均采用相互作用(Interaction)约束，采用硬接触(Hard Contact)和罚摩擦，摩擦系数取0.3；所有钢筋与混凝土、栓钉与混凝土均采用内置区域(Embedded)约束。边界条件和荷载均通过参考点(Reference point)施加：基础梁底面设置刚体(Rigid)约束，固定参考点的6个自由度；除底面外，加载梁其余五个面设置刚体(Rigid)约束，固定参考点的3个自由度(U2,UR1,UR3)，并对参考点施加固定的竖向荷载(U3方向)；对加载梁侧面中点施加位移约束(U1方向)，以实现低周反复试验过程。所有模型在计算全过程中的动能与内能、伪应变能与内能的比值均在5%以下，模型具有良好可靠性，可用于准静态分析。图2展示了CSW-6试件试验与有限元滞回曲线的比较。

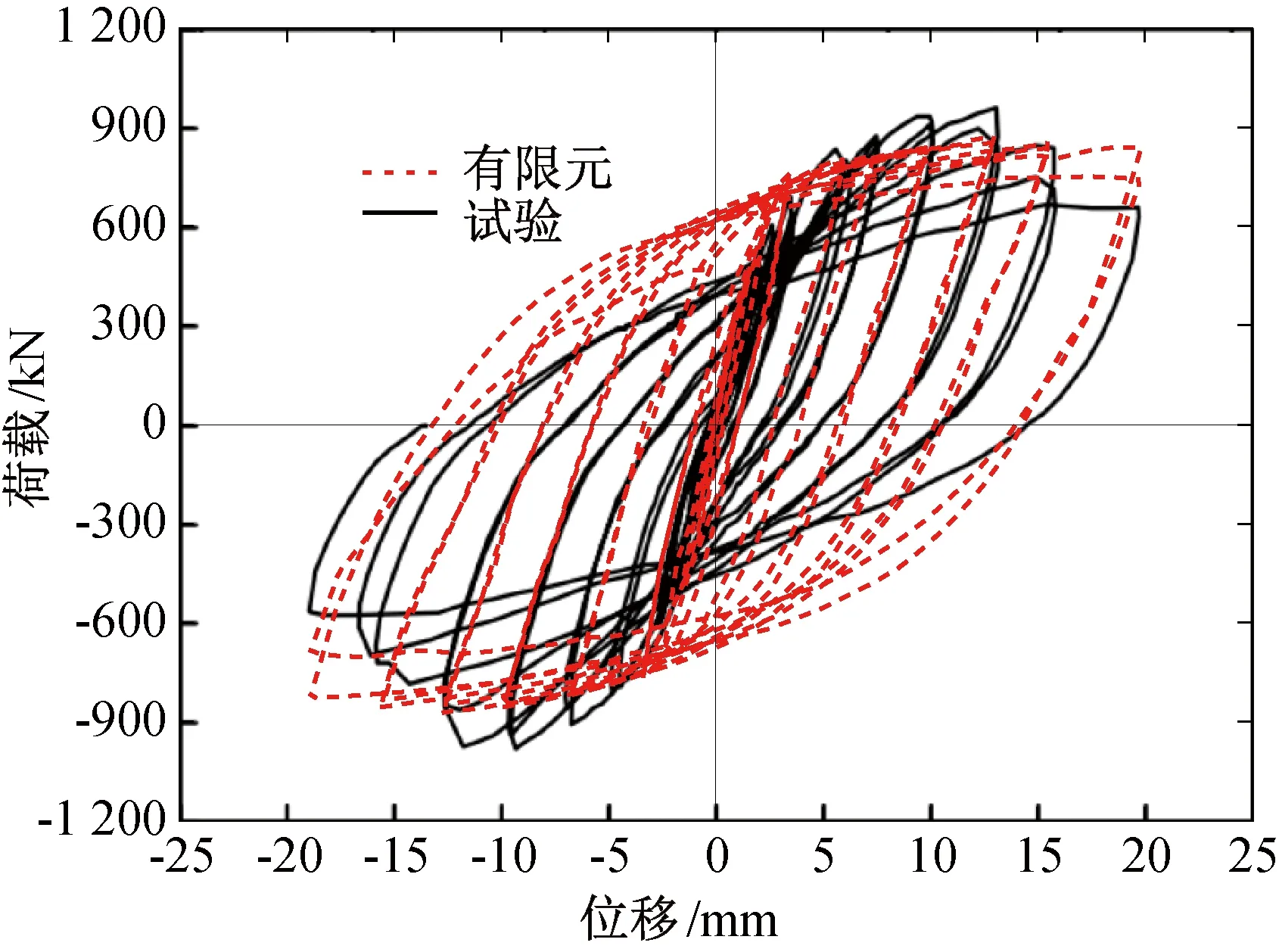
图2 试件CSW-6滞回曲线的比较[15]Fig.2 Comparison of CSW-6 hysteresis curves[15]

1.2.2 边界条件的影响

在有限元中，除了合理的材料本构定义，还原试验情况下的边界条件同样是能否较好地还原试验结果的关键之一。文献[14-15]的试验装置如图3所示。试验中的竖向千斤顶与横梁之间设置滑动支座，以保证竖向千斤顶可随着试件顶部侧移而移动。但是当试件加载梁水平位移较大时，有限元结果表明，加载梁发生了较大的平面内转角UR2，此时由于竖向千斤顶的存在，在加载中千斤顶可能会对结构造成附加弯矩，影响加载梁平面内的自由转动，而在卸载中，可以认为附加弯矩不再存在，加载梁重新自由转动(图4)。根据上述描述的情况，对有限元模型的加载梁UR2进行约束调整。

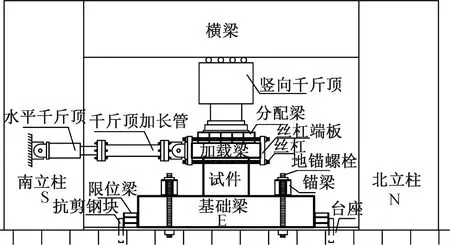
图3 文献[14-15]的试验装置Fig.3 Test device in references[14-15]

图4 大位移情况下竖向千斤顶施加轴压图Fig.4 Axial loading of specimen under large displacement

图5展示了调整前后的有限元模型结果与试验结果的对比，主要对比了滞回曲线和骨架曲线。CSW-6B是调整后的模型，CSW-6A是调整前的模型。总体看来，调整后，试验与有限元结果吻合更好：滞回曲线出现较大地变化，强化阶段的承载力提升更加显著，提高12.1%，但是累积耗能反而减小了2.27%。这表明，构件的抗力可以由边界条件、材料属性等内外部因素共同决定，而构件的耗能能力只会由材料本身决定。

图5 调整加载梁边界条件前后的模型结果[15]Fig.5 Model results before and after adjusting boundary conditions of loading beam[15]

1.3 火灾后的方形CFST柱试件

由于目前火灾后CFDSPC剪力墙的拟静力试验较少，并且已有的试验[9]缺少钢材和混凝土的所有相关力学参数，虽然在文献[10]中补充了文献[9]中火灾后抗震试验的钢板和混凝土的力学参数，但仍未给出重要的连接件力学参数。因此本文采用火灾后CFST柱的拟静力试验验证火灾后的材料本构模型。

对林晓康[16]报道的5个方形CFST柱拟静力试验进行模拟，其中4个为火灾后的试件，1个为未受火灾的试件。需要指出的是，该批方形CFST柱的火灾试验均是在无轴压状态下进行的。

1.3.1 模型建立

火灾温度场模型的建模方式与第1.1节相同，这里不再阐述。

火灾后力学模型的单元类型、约束方式与第1.2.1节基本相同，这里不再阐述。边界条件和荷载均通过参考点(Reference point)施加：两端采用铰接，约束加载平面外的4个自由度；跨中加载端设置为刚体(Rigid)约束，对参考点施加往复位移。

1.3.2 结果对比

图6为部分CFST柱滞回曲线的比较，可以看出：轴压力较小的试件(SF1)，滞回曲线的计算结果与试验结果吻合较好；当轴压力较大时，有限元可以较准确地还原出试验的初始刚度，但无法有效模拟出试验的强化阶段和强度退化阶段，试件将提前进入下降段。这可能是由于试验中施加了较大的轴压力，在平板铰位置产生了较大的摩擦力，抑制了两端平板铰的自由转动，延缓了钢板发生屈曲的时间，最终导致试件峰值荷载偏大于模拟结果，下降段偏迟于模拟结果。

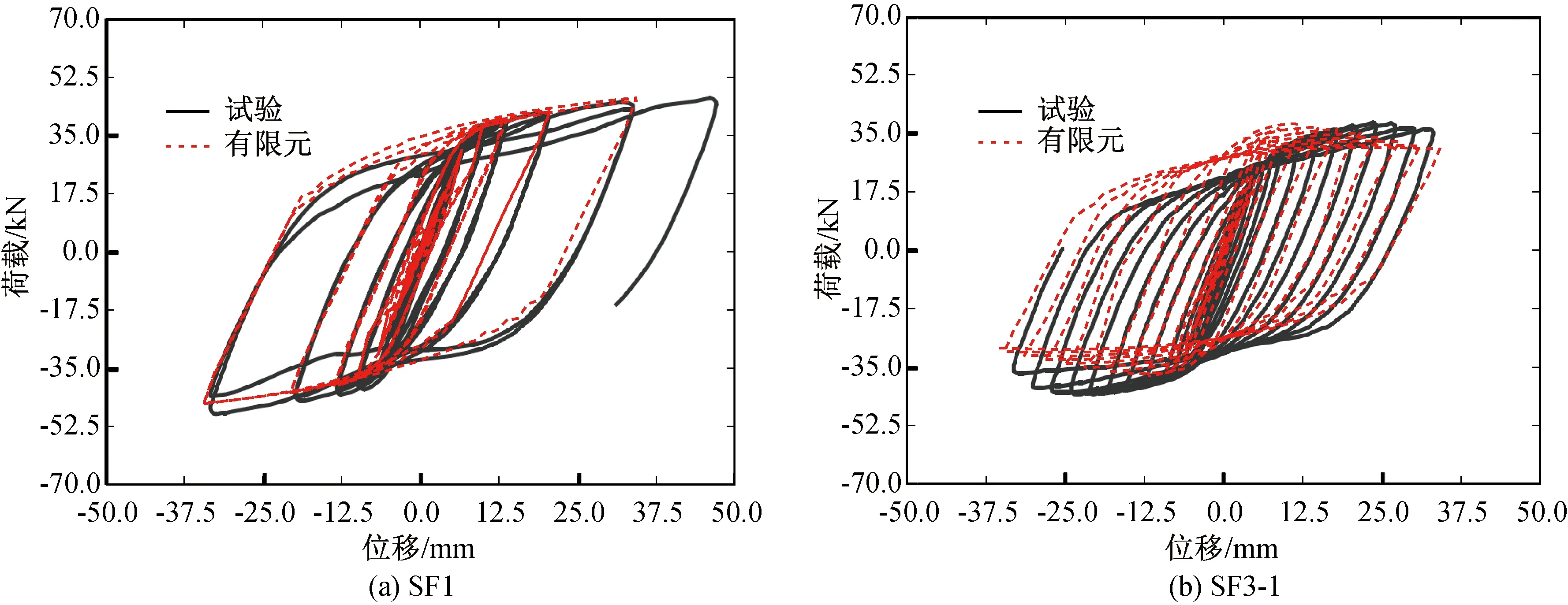
图6 部分柱滞回曲线的比较[16]Fig.6 Comparison of partial column hysteresis curves[16]

图7展示了CFST柱在破坏形态方面的对比，选取了有限元模型SF4-1的破坏照片作对比。有限元和试验均是在柱的跨中加载端附近发生破坏，主要表现为钢管屈曲和屈曲位置的内部混凝土破坏。因此，火灾后模型同样能较好地模拟火灾后CFST柱的滞回行为，模型可用于火灾后CFDSPC剪力墙的有限元研究中。

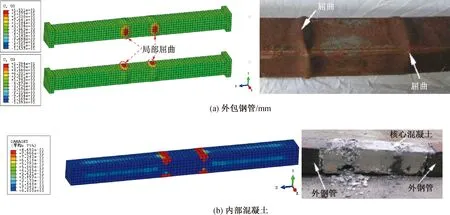
图7 典型 CFST 试件的破坏形态[16]Fig.7 Failure modes of typical CFST specimens[16]

2 火灾后双钢板-混凝土组合剪力墙抗震性能研究及参数分析

利用上节的有限元建模方法及材料本构模型，以中国南方航空大楼的CFDSPC剪力墙为原型建立足尺抗震性能分析模型，对火灾后CFDSPC剪力墙的破坏形态、承载力、变形能力以及延性等抗震性能指标进行分析，最后通过单调加载方式，对火灾后CFDSPC剪力墙的初始刚度、承载力以及变形能力进行参数分析。

2.1 足尺 CFDSPC 剪力墙模型

2.1.1 模型基本尺寸

CFDSPC剪力墙模型将根据中国南方航空公司大楼的CFDSPC剪力墙设计其施工现场如图8(a)所示。该建筑中的CFDSPC墙体基本信息如下[17]：墙体高度为4 400 mm，宽度为2 575～3 300 mm，厚度为220～400 mm；钢板厚度为12 mm；墙体剪跨比为1.33～1.71；墙体设计轴压比为0.3～0.7。最终确定有限元模型的基本信息如下：墙体高度分别为2 650、3 500和4 400 mm，墙体宽度为2 640 mm，厚度取220 mm，剪跨比为1、1.33和1.67；钢板 厚度为8～12 mm；实际轴压比为0～0.4，其设计轴压比约为0～0.6。该建筑墙体的内部连接件采用横向窄加劲肋和板条，墙体两侧的边柱采用方形CFST柱，如图8(b)所示。模型中，并未采用该种布置形式，而是采用直径为20 mm的拉杆作为抗剪连接件，间距为100 mm。

图8 南航大厦中的 CFDSPC 剪力墙[17]Fig.8 CFDSPC shear wall in Nanhang building[17]

本节将研究火灾时间、轴压比、剪跨比、墙体截面配钢率、混凝土抗压强度等参数对火灾后CFDSPC剪力墙抗震性能的影响，其余参数均为固定参数，各参数的具体取值详见表1。

表1 火灾后模型参数Tab.1 Model parameters after fire

试件编号规则如下：例如，试件N4T12H4400C40t12，即表示为n=0.4，th=120 min，Hw=4 400 mm，fcu=40 MPa，t=12 mm的试件。

2.1.2 截面最高温度分布

火灾后钢材和混凝土的残余力学性能主要取决于其经历的最高温度，因此，采用基于Fortran编制的ABAQUS子程序VUSDFLD来提取升降温过程中每个节点经历的最高温度，将其导入抗震分析模型以进行火灾后的力学性能计算。图9展示了60～180 min火灾后模型中钢板、混凝土的最高温度分布情况。可以看出：(1)60～180 min火灾后，钢板的最高温度分别为826 ℃、985 ℃和1 071 ℃(强度分别折减11.7%、20.4%和26%，刚度分别折减11.7%、20.4%和26%)，最低温度分别为78 ℃、106 ℃和123 ℃；(2)60～180 min火灾后，混凝土的最高温度分别为641 ℃、841 ℃和950 ℃(强度分别折减57.92%、88%和94%)，最低温度分别为83 ℃、114 ℃和132 ℃；(3)墙体各位置的最高温度沿墙体厚度方向分布较为均匀，同一厚度下，钢板附近的温度高于其他位置。

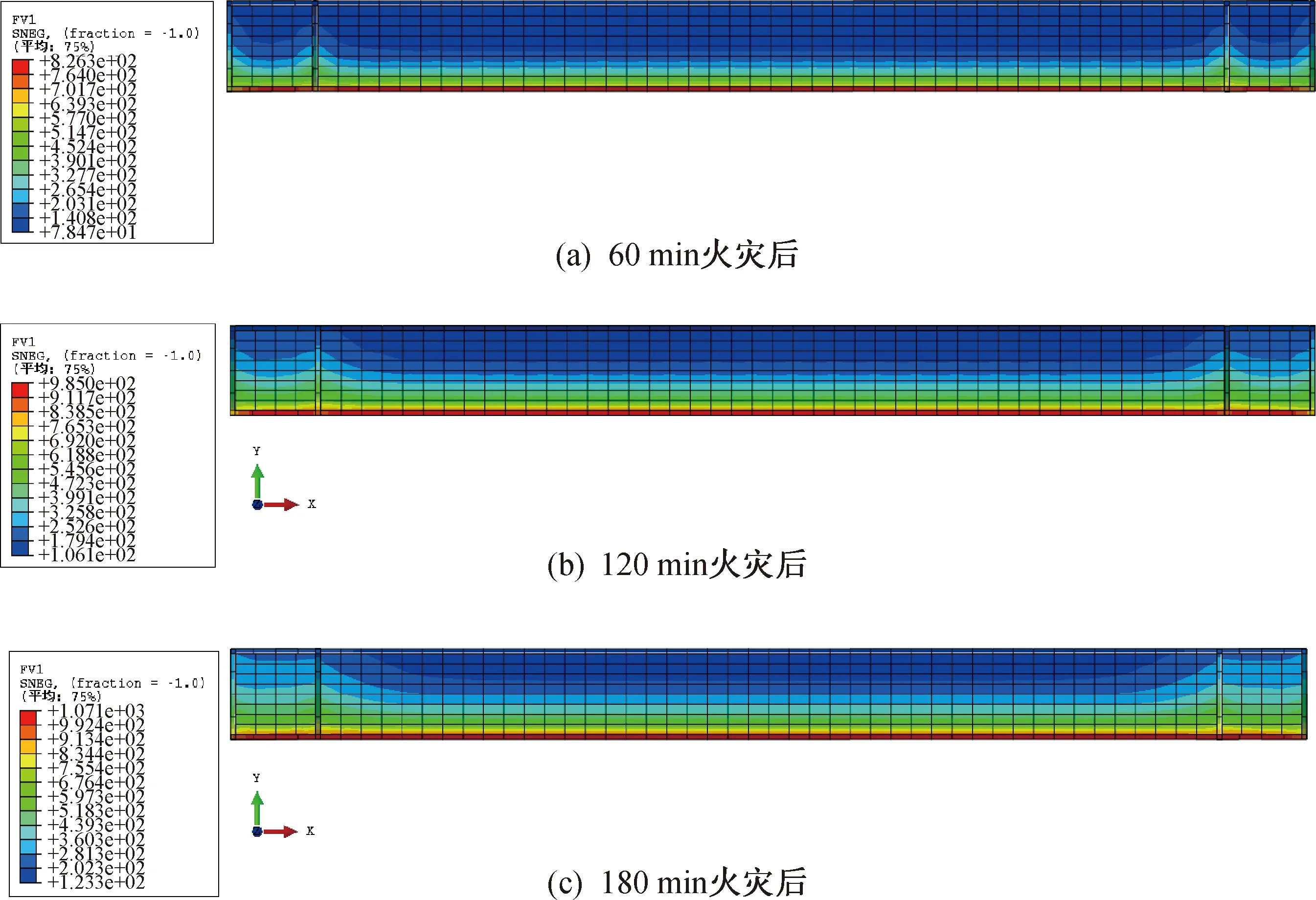
图9 不同火灾时间后截面最高温度分布情况(单位：℃)Fig.9 Maximum temperature distribution of cross section after different fire time

2.1.3 加载制度影响

图10展示了火灾前后CFDSPC剪力墙荷载-位移滞回曲线与单调加载曲线的对比。可以看出：(1)相比于单调加载的墙体，循环加载的墙体提前进入承载力退化阶段，这是由于循环荷载导致两端的混凝土严重损伤，两端的钢材塑性应变积累而迅速断裂；(2)在峰值前，对于无轴压的墙体，其单调加载曲线与循环加载的骨架曲线接近，而对于0.4轴压比的墙体，其单调加载曲线的塑性阶段刚度偏低于循环加载的骨架曲线。针对这一现象，对比分析了墙体在同一位移下的应力状态，表明：在循环荷载下的钢材塑性应变累积导致同一位移下的钢材应力大于单调加载情况下的钢材应力，并且轴压引起更大的应力提高。

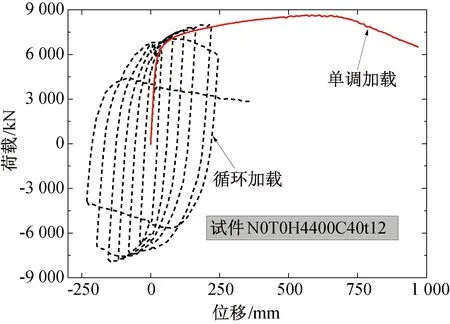
图10 荷载-位移滞回曲线与单调加载曲线的对比Fig.10 Comparison of load-displacement hysteresis curve and monotonic loading curve

由于循环加载受到加载制度的影响，且较难进行计算下降段的计算，因此在后续分析中，采用单调加载制度代替循环加载，来研究火灾时间、轴压比、高厚比等参数对刚度、承载力、变形能力等指标的影响。

2.2 参数分析

2.2.1 火灾时间的影响

图11展示了火灾时间对荷载-位移曲线的影响，选取了n=0和0.4的两组试件。图12对比了不同轴压比下的墙体，其经历的火灾时间对初始抗剪刚度和抗剪承载力的影响。可以看出：(1)随着火灾时间的加长，墙体在火灾后的初始刚度和抗剪承载力越低，并且当轴压比越大时，火灾时间的影响越显著：对比未火灾的墙体，当n=0时，180 min的火灾导致初始抗剪刚度和抗剪承载力分别退化16.9%和7.2%，而当n=0.4时，其值分别退化了23.0%和11.7%；(2)当n=0时，火灾时间的增加并未改变荷载-位移曲线的整体形状，但是对于n=0.4的墙体，当火灾时间增加到120和180 min时，墙体的变形能力急剧退化，这是由于高温降低了受火侧材料的性能，致使墙体在高轴压比、大变形下迅速朝着整体刚度较小的受火侧压塌破坏，如图13(a)所示。

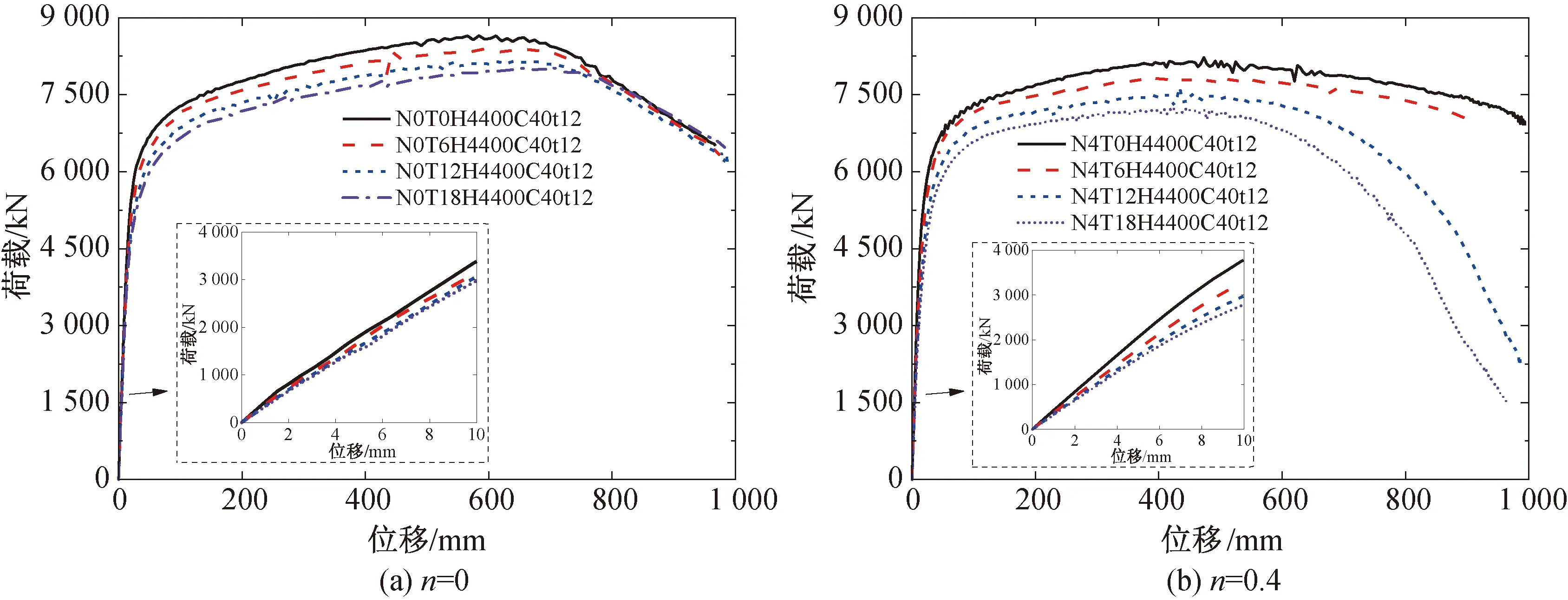
图11 受火时间对荷载-位移曲线的影响Fig.11 Influence of fire time on load-displacement curve

图12 受火时间对初始抗剪刚度和抗剪承载力的影响Fig.12 Effect of fire time on initial shear stiffness and shear bearing capacity

图13 单调加载下的墙体典型破坏模式 (单位: MPa)Fig.13 Typical failure mode of wall under monotonic loading

图13展示了典型试件的整体破坏形态，主要分为以下两类：(1)试件N4T12和N4T18在受压侧边柱底部发生局部受压鼓曲，随后受压侧墙体整体失稳，其破坏形态如图13(a)所示；(2)而其余六个试件的受压侧钢板鼓曲，受拉侧钢板严重拉变形，其破坏形态如图13(b)所示。可见，对于高轴压比下的CFDSPC墙体，火灾对墙体抗震性能的影响更加严重，需在灾后评估中重点关注。

2.2.2 轴压比的影响

图14展示了轴压比对剪力-位移曲线和弯矩-位移角曲线的影响，选取了th=0和180 min的两组试件。弯矩和位移角的计算方法见图14(a)中的小图。可以看出，与循环加载下的结论相似：除了整体失稳破坏的试件N4T18H4400C40t12，增大轴压比(从0到0.4)均有效提高了墙体的面内抗弯承载力和变形能力，并且对面内抗弯承载力的影响几乎是线性的，如图14(a)和(b)所示。但不同的是，循环加载的试件N4T18H4400C40t12变形能力优于试件N0T18H4400C40t12，而单调加载的N4T18H4400C40t12变形能力却劣于试件N0T18H4400C40t12，这是由于相对于循环加载，单调加载时的位移更大，P-△效应造成了轴压力对墙体变形能力的消极作用。对于墙体的抗剪承载力，0.2和0.4的轴压比均减小了墙体的抗剪承载力，但对初始抗剪刚度的影响不大。

图14 轴压比对剪力-位移曲线和弯矩-位移角曲线的影响Fig.14 Effect of axial load ratio on shear-displacement and moment-displacement angle

2.2.3 剪跨比和高厚比的影响

通过改变墙体高度，来实现剪跨比和高厚比的变化。表2为不同高度墙体的剪跨比和高厚比计算结果，墙体的高厚比为墙体计算高度与厚度的比值。针对处在高层建筑中较低层的高轴压比CFDSPC墙体进行研究。图15展示了剪跨比对弯矩-位移角曲线的影响，选取了th=0和180 min的两组试件。可以看出：(1)随着剪跨比的增大，CFDSPC剪力墙的抗弯刚度降低，但不显著；(2)对于未受火灾的墙体，剪跨比从1提高至1.33，可有效增大墙体的抗弯承载力和变形能力，但是剪跨比从1.33提高至1.67，对墙体的抗弯承载力影响较小；(3)对于高厚比为7.95和10的墙体，单面火灾造成了墙体受火面和背火面的强度、刚度不对称，墙体高厚比较大的消极影响最终导致墙体的抗弯承载力和变形能力降低。因此，对于高厚比较大的CFDSPC墙体，火灾对抗震性能的影响更加严重，需在灾后评估中重点关注。

表2 不同高度墙体的剪跨比和高宽比计算结果Tab.2 Calculation results of shear span ratio and height-width ratio of walls with different heights

图15 剪跨比对弯矩-位移角曲线的影响Fig.15 Influence of shear span ratio on moment-displacement angle curve

2.2.4 墙体截面配钢率的影响

通过改变钢板厚度实现墙体截面配钢率的变化，保持轴压比不变。同样针对处在高层建筑中较低层的高轴压比CFDSPC墙体进行研究。图16展示了墙体截面配钢率对单调加载下弯矩-位移角曲线的影响，选取了火灾时间为0和180 min的试件进行对比。可以看出：增大截面配钢率可以线性地提高墙体的初始刚度、抗剪承载力，但对变形能力的影响不大，并且对墙体在火灾前和火灾后的破坏形态、曲线形状没有太大影响。图17展示了不同截面配钢率的墙体在180 min火灾后，抗剪刚度和承载力的退化程度。可以看出：(1)由于火灾导致的墙体抗剪承载力退化的程度与墙体截面配钢率无关；(2)墙体截面配钢率的提高减小了由于火灾导致的墙体初始刚度退化程度，这是由于钢材在火灾后的弹性模量恢复优于混凝土，增大钢材对墙体初始刚度的贡献就意味着增大了火灾后初始刚度的恢复程度。

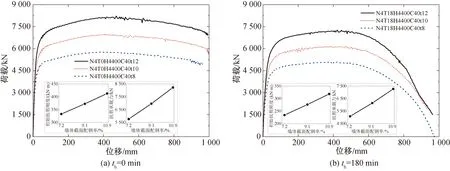
图16 截面配钢率对荷载-位移曲线、刚度和抗剪承载力的影响Fig.16 Effect of section steel ratio on load-displacement curve, stiffness and shear capacity

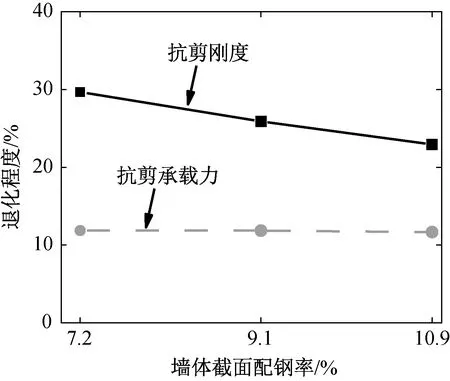
图17 180 min火灾对抗剪刚度和承载力的退化影响程度Fig.17 Effect of 180 min fire on shear stiffness and bearing capacity degradation

3 结论

1) 对于未受火墙体，增大轴压比和剪跨比能够提高墙体的抗弯承载力和变形能力；增大墙体配筋率可以提高抗弯承载力，但对变形能力影响不大。

2) 随着火灾时间的加长，墙体在火灾后的初始刚度和抗剪承载力越低。当轴压比越大时，火灾时间的影响越显著。

3) 高厚比和轴压比较大的墙体在长时间火灾后，其破坏模式将转变为墙体整体迅速朝着受火侧失稳，抗震性能急剧退化。

4) 对于弯曲破坏的墙体，火灾增大了墙体的变形能力，对于压弯破坏的墙体，火灾引起的墙体整体失稳将削弱了墙体的变形能力。