橡胶混凝土受压破坏机理的余能基面力元分析

付 毓，马东翼，王 耀

(北京工业大学 城市建设学部，北京 100124)

当今社会汽车更新速度很快，造成了大量轮胎的废弃，对环境造成了严重的污染。将废旧轮胎切碎、粉磨制成的橡胶混凝土是一种满足可持续发展的绿色建筑材料，如果将其充分应用，不仅解决了大量废旧轮胎堆积问题，还可以保护环境。橡胶粒或橡胶粉作为浇筑材料制备成的橡胶混凝土具有抗冲击性能好、韧性强、抗腐蚀能力强的优点，因而受到国内外学者的广泛关注，并渐渐被应用于工程中。

宏观试验是研究橡胶混凝土的基本手段，1993年，Eldin等[1]首先讨论了橡胶颗粒对混凝土抗压和抗折强度的影响，研究表明，橡胶混凝土的强度随橡胶含量的增加而降低，但韧性和吸能能力显著增加。2004年，熊杰等[2通过试验也得到了相同结论。Toutanji[3]通过试验研究了橡胶含量和粒径对混凝土受压性能的影响，表明橡胶粒径的影响占主导地位。刘峰等[4]通过大量试验提出了橡胶混凝土的强度公式，并根据实测应力-应变曲线，提出了有参数的单轴受压本构方程。相对宏观试验，橡胶混凝土的数值分析研究起步较晚。2006年，刘春生等[5]在细观层面上将橡胶混凝土看成由粗骨料、橡胶骨料和水泥浆组成的三相复合材料进行计算分析。2016年，王娟等[6]在前人基础上考虑了骨料与砂浆的界面和初始缺陷，建立了考虑初始缺陷的橡胶混凝土计算模型。杨朝霞[7]在此基础上研究了橡胶掺量、粒径和界面缺陷含量对橡胶混凝土力学性能的影响。薛刚等[8]利用ABAQUS模拟橡胶混凝土内部裂纹的发展过程。

以往对橡胶混凝土的模拟都是基于常规的势能原理有限元法，而基于余能原理有限元方法的研究尚未见报道。基于余能原理基面力元法[9]研究橡胶混凝土力学性能，既扩展了该方法的应用范围，也为橡胶混凝土的模拟提供一种新的可能。本文将橡胶混凝土视为由粗骨料、橡胶颗粒、砂浆、粗骨料与砂浆界面、橡胶与砂浆界面组成的五相介质复合材料。使用Fortran程序生成橡胶混凝土二维混合随机骨料模型。基于余能原理基面力元法进行受力分析，获得了压缩应力-应变曲线图，并将数值模拟结果与试验数据进行对比。研究了橡胶颗粒大小和含量对橡胶混凝土抗压强度的影响，绘制了缝纹发展过程图，分析其破坏机理。

1 余能原理基面力元法

传统的余能原理有限单元法构造单元的应力插值函数需要满足的平衡条件较多，积分求解单元的柔度矩阵计算量大，效率低，导致余能有限元法的应用受限。2003年，高玉臣[10]提出了基面力的概念，与传统的应力张量比较，它的表达简洁，采用直接表达法表示柔度矩阵，避免了复杂的运算。彭一江[9]基于这个理论思路建立了基于余能原理的基面力元法，提高了计算效率。

余能原理基面力单元法的核心是单元柔度矩阵的生成[9]，本文采用四边形边中节点基面力单元，如图1所示。

图1 四边形边中节点单元Fig.1 Quadrilateral element with node at midpoint

TI，TJ，TM，TN为作用在各边中节点上的面力的合力。柔度矩阵显式表达式推导过程如式(1)—(5)所示。平面单元的平均应力为

(1)

式中：PI—原点指向边中节点的径矢。

单元余能为

(2)

式中：E—弹性模量，GPa；v—泊松比；U—单位张量。

二维单元余能为

(I,J=1,2,3,4)

(3)

式中：A—单元面积；I、J—单元的第I边与第J边；pIJ—PI和PJ的点积。

TI对应的广义位移δI为

(4)

式中：CIJ—单元柔度矩阵显式表达式。

(I,J=1,2,3,4)

(5)

2 细观数值模型

2.1 橡胶混凝土混合随机骨料模型

本文在细观层次上将橡胶混凝土视为由天然骨料、橡胶、砂浆、骨料-砂浆界面、橡胶-砂浆界面组成的五相复合材料。其中粗骨料是混凝土的重要组成部分，骨料形状作为骨料重要特征之一，对混凝土力学性能的影响不可忽视。目前已有的橡胶混凝土随机骨料模型，通常将骨料简化成圆形[5-8]。虽然这种简化在一定程度上是合理的，但与骨料实际形状仍有很大差异，无法表征骨料棱角位置的应力集中现象。

本文建立了尺寸为100 mm×100 mm橡胶混凝土二维模型，将粗骨料分为20～15 mm、15～10 mm、10～5 mm三个粒径范围，由Walraven公式[11]确定橡胶混凝土模型中各粒径范围圆形骨料的面积，并根据代表粒径计算圆形骨料数量。现分别用平均粒径4 mm和2 mm的橡胶粒按10%、20%、30%掺量等体积替代细骨料，细骨料含量由实验[12-13]计算得到，如式(6)，从而算出橡胶颗粒数量。各粒径范围粗骨料数及橡胶颗粒数见表1、表2。随后根据蒙特卡罗法投放骨料，生成随机圆骨料模型，如图3(a)所示。

表1 粗骨料颗粒数Tab.1 Number of coarse aggregate particles

表2 不同粒径及掺量下橡胶颗粒数Tab.2 Number of rubber particles under different particle size and content

Ps=ms/ρs=780/2 650≈0.3

(6)

式中：Ps—细骨料占混凝土体积分数；ms—单位体积中细骨料质量，kg/m3；ρs—细骨料表观密度，kg/m3。

随后，在圆形骨料试件模型的基础上，利用多边形骨料生成方法[14]，仅在粗骨料的圆内生成内接多边形，形成基框架，控制各边的最小长度Lmin，使骨料圆心在生成的多边形内部。

Lmin=2R·sin(π/2(n-1))

(7)

式中：Lmin为最小边长；R为骨料半径；n为多边形基框架顶点数。

之后从基框架较长边开始延展，在以边长为直径的圆内插入随机点P，P点坐标为

(8)

式中：E、F为(0,1)内的随机数。

依次将每个圆的基框架向外延展，保证延展后的骨料不与其他骨料和橡胶颗粒重合，直至达到圆的面积。凸骨料生成过程如图2所示，橡胶混凝土凸骨料与圆形橡胶混合投放随机骨料模型如图3(b)所示。

图2 凸骨料生成过程Fig.2 Convex aggregate formation process

图3 橡胶混凝土随机骨料模型Fig.3 Random aggregate model of rubber concrete

本文选取二维四边形单元网格剖分方法，为尽量准确模拟界面单元，网格剖分尺寸取0.5 mm。将网格投影到随机骨料模型中，根据单元节点在网格内的数量对单元进行判断并赋予单元属性。

2.2 本构模型

骨料与橡胶颗粒在小变形下为线弹性，采用线弹性本构关系。

砂浆及界面在接近峰值应力时，会出现非线性特征，为更好模拟其力学性能，采用多折线受压损伤本构模型[15]如图4 所示。

图4 多折线受压损伤本构模型Fig.4 Multi polygonal line compression constitutive model

在受压损伤本构模型中，材料的受压损伤变量记为Dc，Dc见式(9)：

(9)

式中：εc0为峰值应变，λ为弹性应变系数，γ为残余应变系数，η为极限应变系数，α为弹性抗压强度系数，β为残余抗压强度系数。

2.3 材料参数

骨料和橡胶颗粒的材料参数由文献[16,17]确定，砂浆的材料参数由参考文献[18]中的经验公式确定：先将试验[12]中橡胶混凝土水灰比代入式(10)，求得抗压强度，再将抗压强度代入式(11)、(12)，求得砂浆弹模和抗拉强度。根据文献[19-20]，骨料与砂浆界面参数为砂浆材料参数的65%，橡胶与砂浆界面参数为砂浆材料参数的35%。各相介质材料参数取值见表3。

表3 各相介质材料参数Tab.3 Material parameters of each phase medium

(10)

Em=1 000(7.7ln(fc)-5.5)

(11)

ft=1.4ln(fc)-1.5

(12)

式中：Em—砂浆弹性模量，GPa；ft—砂浆抗拉强度，MPa；fc—砂浆抗压强度，MPa；w/c—水灰比。

3 数值模拟及破坏机理分析

3.1 加载模型

本文对100 mm×100 mm试件进行二维单轴压缩数值模拟。为了减少骨料分布对力学性能的影响，在骨料与橡胶颗粒含量不变的情况下，进行三次随机投放，生成三个混合随机骨料模型，如图5所示。图中灰色为砂浆，青色为骨料，黑色为橡胶颗粒，白色为界面。

图5 模型示意图Fig.5 Schematic diagram of model

采用如图6所示的加载模型进行加载。限制底部所有点的竖向位移。为了避免刚体移动，限制底部中间节点的水平位移。加载方式为等位移增量加载，加载步长为0.01 mm /加载步。

图6 受压加载模型Fig.6 Compression loading model

3.2 试验对比

采用余能原理基面力元法进行受力分析，获得了应力-应变曲线。以应力与峰值应力σ0的比值为纵坐标，以应变与峰值应变ε0的比值为横坐标，绘制橡胶混凝土归一化应力-应变曲线图，并与试验结果[12]进行比较，如图7所示。

图7 橡胶混凝土归一化应力-应变曲线Fig.7 Normalized stress-strain curve of rubber concrete

三个不同试件的峰值应力分别为16.07、17.01 和16.66 MPa，平均峰值应力为16.58 MPa，与胡艳丽等试验数据[12]吻合较好，其中试验实测值为16.45 MPa，与本文结果相差在4%以内；平均值与试验数据仅相差0.7%。

通过对比可以发现，数值模拟结果和试验的抗压强度相差不大，应力-应变曲线在上升段拟合良好，但下降段数值模拟结果比试验结果略缓，这可能是因为实际中混凝土有较多孔隙和缺陷，这些缺陷会使混凝土更易发生脆性破坏，所以强度降低较快。对比结果初步验证了使用余能原理基面力元法计算该模型的合理性与正确性。

3.3 破坏机理分析

采用Fortran程序绘制一个橡胶混凝土模型破坏过程图，如图8所示。图中砂浆为浅灰色，骨料为红色，橡胶为蓝色，界面单元为白色，损伤单元为深灰色，破坏单元为黑色。

图8 模型破坏过程图Fig.8 Model failure process

由图可知，破坏单元最开始出现在橡胶与砂浆界面处。随着进一步加载，粗骨料与砂浆的界面出现破坏，同时相邻较近的橡胶之间的砂浆开始破坏，形成明显的裂缝，裂缝在橡胶颗粒较为密集的区域开始发展。继续加载，当试件到峰值强度附近时，粗骨料与砂浆的界面开始大量破坏，橡胶周围的裂缝会和附近的粗骨料与砂浆界面的裂缝连通，形成更长的裂缝。随后裂纹变长变宽，最后裂纹贯通呈沙漏状，裂纹与水平夹角为45°～60°。

使用Matlab绘制橡胶混凝土模型不同加载步下最大主应变云图与最大主应力云图，如图9、图10所示。由图可知，加载初期，由于砂浆和粗骨料的弹模远大于橡胶的弹模，橡胶颗粒周围的应力、应变较大。随着加载的进行，出现应力、应变集中现象，橡胶与砂浆界面单元开始破坏。当加载到峰值应力时，应力、应变集中现象加剧，发生应力、应变重分布，破坏单元周围单元应力、应变明显提高，随后开始破坏，导致裂纹扩展连通并变宽，橡胶周围裂缝与骨料界面处裂缝连通。随着加载继续进行，裂缝间相互连通，发生贯穿现象，各处应力均减小，但应变继续增大。

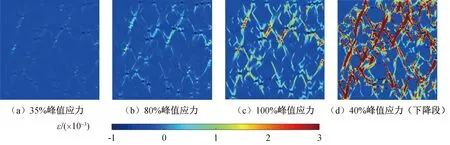
图9 最大主应变云图Fig.9 Maximum principal strain contour plots

图10 最大主应力云图Fig.10 Maximum principal stress contour plots

通过应力分布图，可以看出橡胶附近区域最先出现应力集中现象，因此在制备橡胶混凝土时应当将橡胶颗粒充分分散，以达到更高的抗压强度。

通过应变分布云图，可以直观准确地看出裂纹从出现到发展的全过程，该应力分布特征和破坏图中裂纹特征完全一致，验证了损伤破坏图的正确性。

4 橡胶掺量、粒径对抗压强度的影响

为了研究橡胶掺量、粒径对抗压强度的影响，采用上文建立的橡胶混凝土混合随机骨料模型对橡胶粒径为4、2 mm及掺量分别为0%、10%、20%、30%的橡胶混凝土试件进行单轴压缩数值模拟。模型尺寸为100 mm×100 mm，以掺量为0%的试件作为对照组。为了降低骨料随机性的影响，对每个类型的橡胶混凝土随机投放三次。各试件抗压强度模拟结果见表4。不同粒径、掺量对橡胶混凝土抗压强度的影响如图11所示。

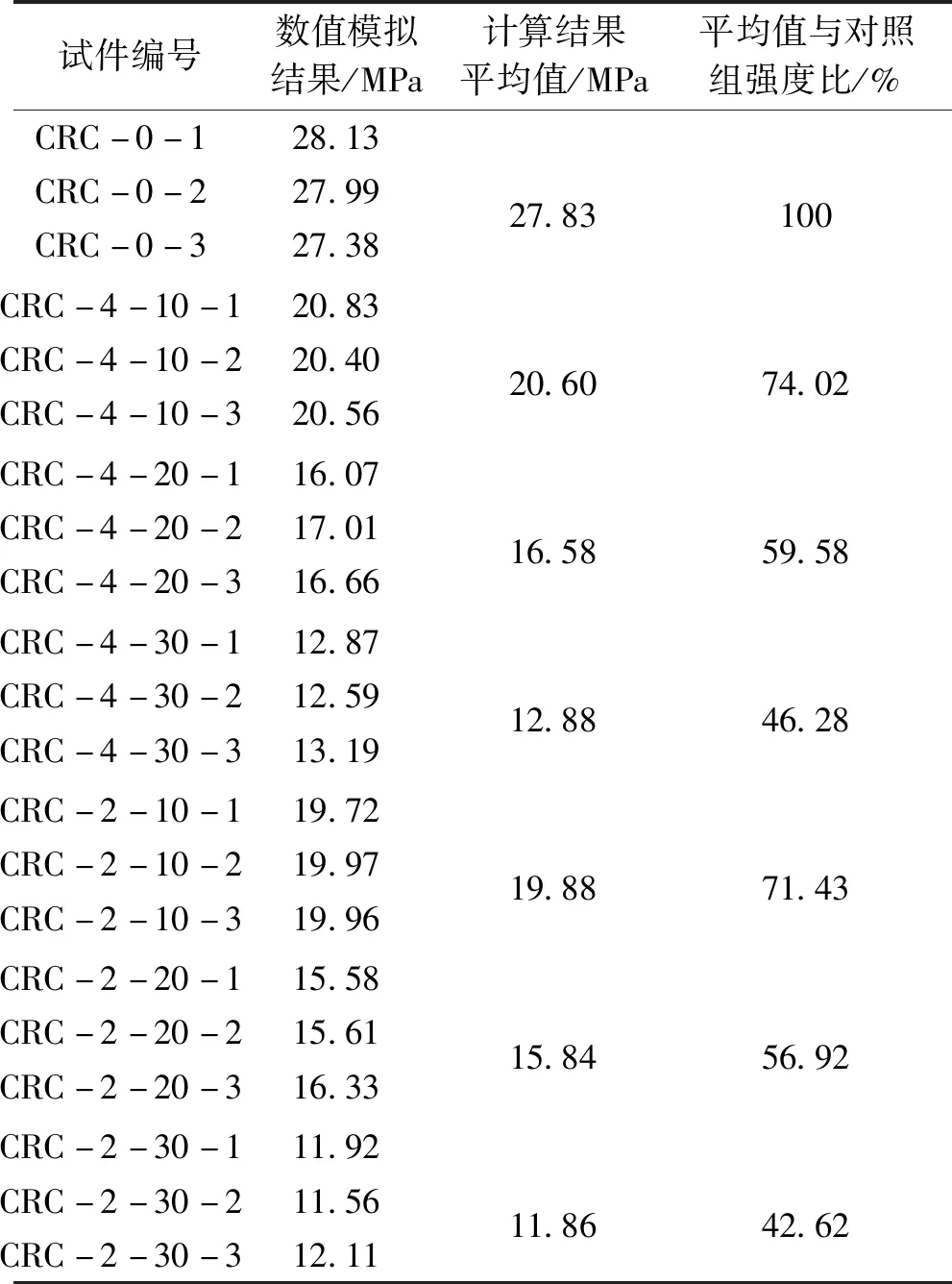
表4 不同橡胶粒径、掺量的橡胶混凝土计算结果Tab.4 Calculation results of rubber concrete with different particle size and content

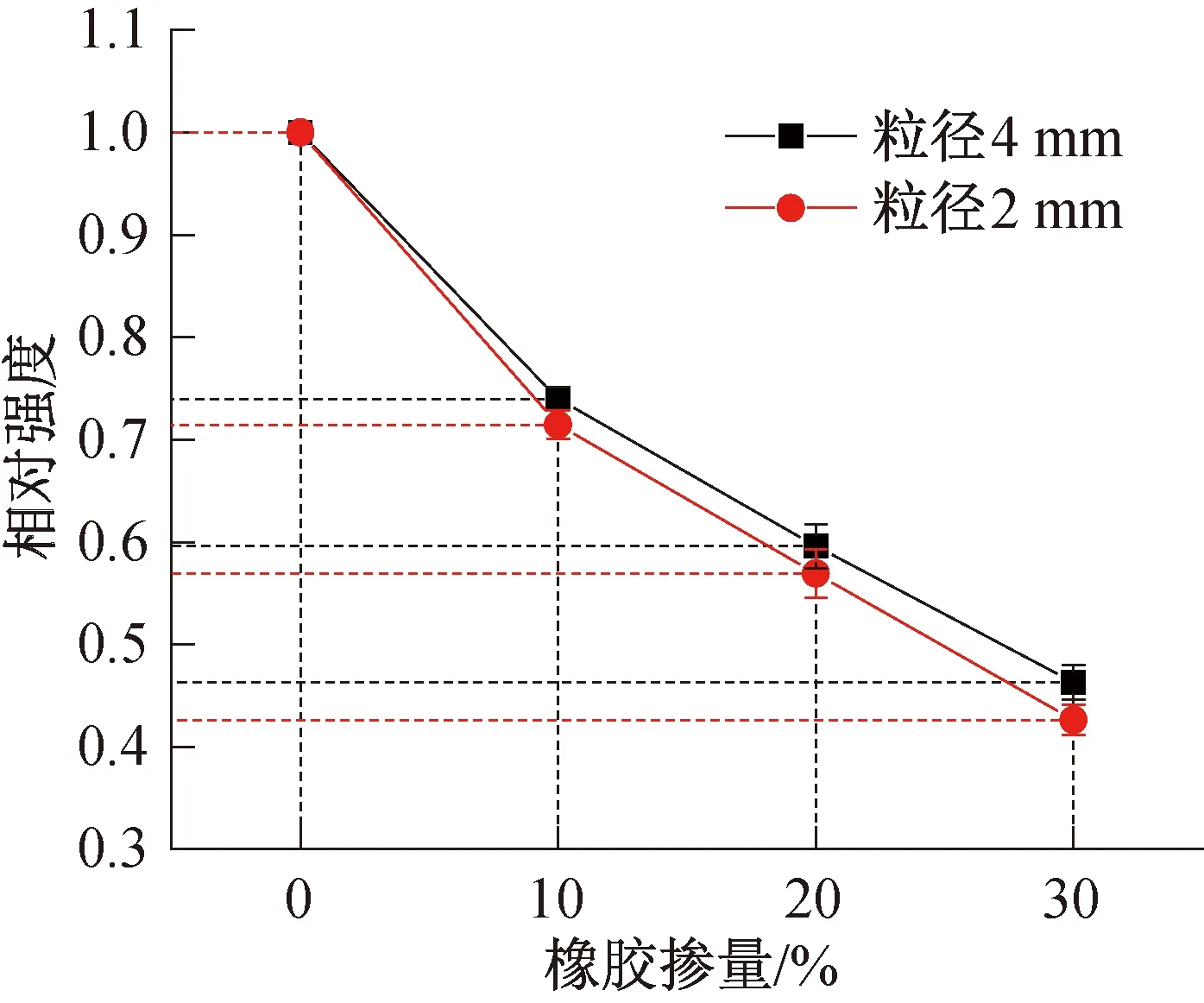
图11 不同粒径、掺量对橡胶混凝土抗压强度的影响Fig.11 Effect of different rubber particle size on compressive strength of concrete

结合表4和图11可知，普通混凝土抗压强度为27.83 MPa，当掺入橡胶粒径为4 mm时，橡胶掺量为10%、20%、30%的橡胶混凝土抗压强度为20.60、16.58、12.88 MPa，分别为普通混凝土的74.02%、59.58%、46.28%；当掺入橡胶粒径为2 mm时，橡胶混凝土抗压强度为19.88、15.84、11.86 MPa，分别为普通混凝土的71.43%、56.92%、42.62%。

由此可见，随着橡胶掺量的增加，橡胶混凝土抗压强度明显降低，最大降低幅度为58%；当掺入10%橡胶时，强度下降速率较大，随着掺量的增加下降速率逐渐降低。橡胶掺量相同时，橡胶粒径为2 mm时的抗压强度略小于粒径为4 mm的抗压强度，并且随着橡胶掺量的增加，这种现象愈发明显。这是因为随着橡胶颗粒粒径的减小，橡胶颗粒的比表面积增大，比表面积的增大导致了橡胶与砂浆之间的界面增多，使橡胶混凝土更易破坏，所以橡胶混凝土的抗压强度降低。

5 结论

1)本文建立橡胶混凝土二维随机混合骨料模型，采用余能原理基面力元法对其单轴压缩过程进行模拟，得到试件的抗压强度与试验数据相差在4%以内，模拟结果平均值与试验仅相差0.7%。说明该模型可以较好模拟橡胶混凝土的力学性能。

2)在单轴静态压缩状态下，橡胶与砂浆界面处发生应力集中，破坏单元最先出现，并在橡胶密集区域连通。随着加载的进行，凸骨料较长的边与砂浆界面开始破坏，并和橡胶密集区域裂缝连通，裂纹破坏加宽加大，裂纹主要方向为45°～60°。

3)掺入的橡胶颗粒粒径相同时，橡胶混凝土的抗压强度随掺量增加而显著降低，且随着橡胶掺量的增加下降速率降低。当橡胶掺量相同时，橡胶粒径4 mm时的抗压强度略大于粒径2 mm的橡胶混凝土，并随着掺量的增加而愈发明显。因此可以得知，橡胶掺量对橡胶混凝土的抗压强度的影响程度显著大于橡胶粒径。