表面自然腐蚀后带缺陷管钢的力学性能研究

卢召红，韩璐泽，徐 艳*，王尊策,2

(1.东北石油大学，黑龙江 大庆 163318； 2.中国石油管道科技研究中心重点实验室，河北 廊坊065000)

油气输送管道是一种特殊的承压装备，如果发生泄漏不仅会带来大量的经济损失，而且泄漏所产生的环境污染会造成更加严重的二次灾害，在高后果区产生的损失更是不可估量。现役管道在运行过程中，由于运输介质的腐蚀性和外部环境的腐蚀作用，会影响管道的力学性能，导致其承压能力减弱，甚至会造成管道穿孔或破坏等后果[1-2]。腐蚀管道钢的力学性能与其锈蚀程度相关，目前，众多学者通过测量最大截面损失率、有效截面厚度或钢材体积损失率等方法对带腐蚀缺陷管钢的剩余强度进行预测评估[3-4]，但对于腐蚀后的钢材变形性能未做细致研究。随着研究的不断深入，人们对于腐蚀钢的本构关系有了进一步的认识[5]。邱斌等[6]利用试验的方法研究腐蚀损失率对钢材力学性能的影响，通过对不同腐蚀程度的Q235试件进行拉伸试验，发现当腐蚀损失率小于4%时，锈蚀缺陷对钢材的屈服强度和抗拉强度没有明显的影响，当腐蚀损失率大于4%时，锈蚀后钢材的屈服强度和抗拉强度随锈蚀率的增大呈现明显的线性退化趋势。退化速率与锈蚀钢板表面锈蚀形貌特征密切有关[7]。Nakai等[8]发现锈坑对腐蚀钢材的强度和延性有显著影响，强度和延性随锈坑深度和密度的增大显著降低。Tatsuro等[9]对点蚀构件进行拉伸试验，得出随着点蚀蚀坑深度的增加，拉伸强度逐渐降低，总延伸率急剧下降。Zhang[10]根据弹塑性断裂力学中的Tresca屈服准则，讨论了均匀腐蚀管道在内压和轴向力共同作用下的剩余强度计算，给出了缺陷尺寸、缺陷下的最大允许工作压力和残余强度的计算公式。在此基础上，提出了基于可靠性的腐蚀管道剩余寿命预测方法。针对现役的钢制输送管道，由于无法精确测量出其腐蚀度和剩余力学性能指标，拟通过研究腐蚀损失率与钢材性能之间的影响，来推算出腐蚀损失程度对管道钢的力学性能的影响。腐蚀损失程度可根据管道所处的环境及保护措施，由腐蚀率推算得到，由此可对管道使用周期内各时间点的力学性能进行评估，为预防在役管道泄漏及维护提供参考依据。

本文通过拉伸试验的方法，分析不同腐蚀程度的API 5L X52N管钢力学性能，研究腐蚀损失率对带腐蚀缺陷管钢力学性能的影响，并分析腐蚀缺陷处的应力集中问题。

1 带腐蚀缺陷管钢材料力学性能试验

1.1 试验方法

试验材料为API 5L X52N管钢，图1(a)所示为埋地管线截取后放置室外自然环境自然腐蚀后的表观现象。图1(b)为带腐蚀的管道钢内表面清洗后的表观现象。

图1 带腐蚀缺陷管道图Fig.1 The piping drawing with corrosion defects

依照《金属材料室温拉伸试验方法》 (GB/T 228.1—2010)[11]和《钢及钢产品力学性能试验取样位置及试样制备》 (GB/T 2975—2018)[12]中对于切取圆钢管拉伸样坯中相关说明来确定拉伸样坯的相关参数，试件尺寸如图2所示。

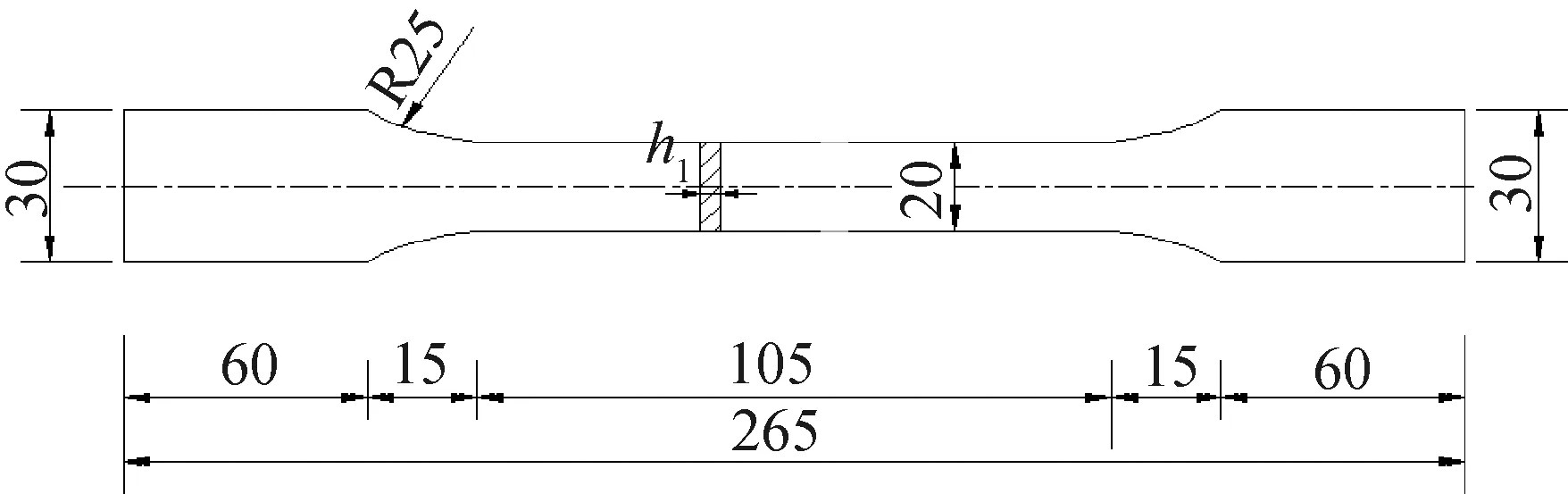
图2 试件设计加工图(单位：mm)Fig.2 The design chart of the specimens

利用失重法测定试件的腐蚀损失率η，建立腐蚀损失率η与腐蚀率ηs的关系。并用SuperView W1三维表面形貌仪扫描试件，借助Pro ENGINEER分析软件获取试件表面几何特征参数。

试验方法和步骤参照《金属材料室温拉伸试验方法》(GB/T 228.1—2010)[11]，主要通过WAW-1000型电液伺服万能试验机、电子引伸计、DH3817Y数据采集系统等仪器对力和变形进行自动采集、记录。试验环境温度为室温。试件加载装置和数据采集系统如图3所示。

图3 试验加载装置和数据采集系统Fig.3 Specimen loading device and data acquisition system

钢材弹性阶段和屈服阶段的加载速率设定为0.75 mm/min，塑性强化阶段的加载速率设定为0.5 mm/min。试件标距设定为50 mm，标距之间的变形利用引伸计进行测量，加载后期为防止引伸计损坏，降低拉伸加载速率为0.25 mm/min，直至试件拉断。试件的泊松比通过测量横向应变与纵向应变值，然后经过计算确定。

1.2 试验结果及分析

根据试验方法测定各试件的数据参数并计算出各试件的腐蚀损失率η，按腐蚀损失率从小到大的顺序给各个试件编号，其中G001为未腐蚀管钢；G10i为腐蚀年限1年的管钢；G20i为腐蚀年限2年的管钢。参照Xu[13]提出的方法，对选取的钢管试样表面腐蚀坑参数进行分析，得出各试样表面的最大腐蚀深度dmax，平均腐蚀深度dav，最大腐蚀坑长度(拉伸方向)lmax，最大腐蚀坑宽度(垂直于拉伸方向)ωmax。按公式(1)计算各试件最大坑深宽比βmax，并标注出位置，测量结果如表1所示。

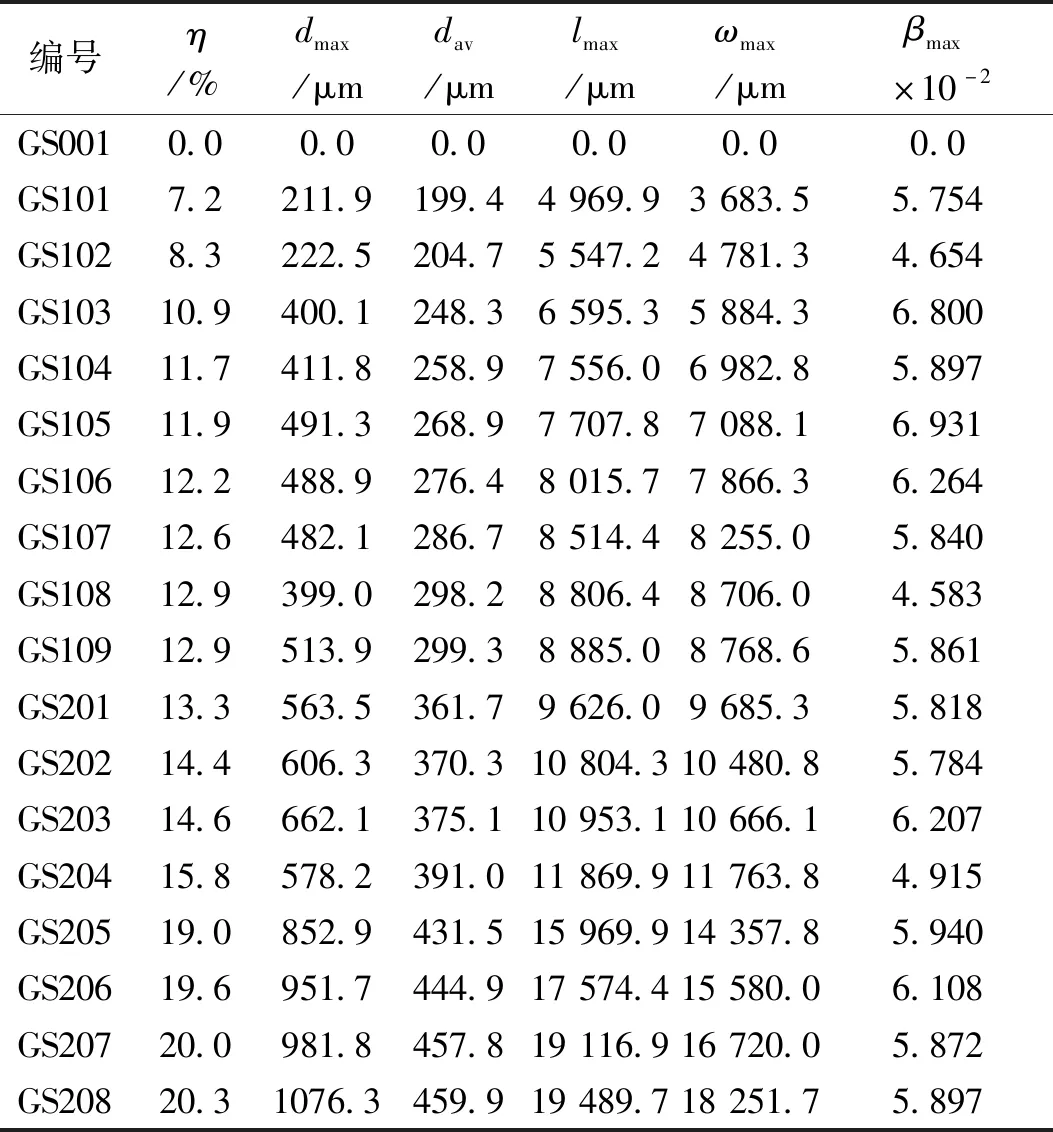
表1 各试件基本参数Tab.1 Basic parameters of each specimen

(1)

图4为试件拉伸破坏形态，各试件拉伸破坏后均有明显的颈缩现象，随着腐蚀损失率的增大，断裂位置由试件中间向两侧不确定方向发展，且具有离散性。断裂位置与腐蚀损失率及腐蚀坑深宽比有关，一般发生在深宽比最大处。

本测区形状为矩形区域，面积约46 km2，测区地势起伏较大，最大地面高差为300 m。航向间隔7条基线布设一个平高控制点，旁向间隔5条航线布设一排平高控制点。按常规像控点布设要求在测区内选择48个均匀分幅的明显地物点作为地面控制点，采用GPS RTK测量方法测定其平面坐标和高程。经检核，各像控点平面精度、高程精度均优于±0.2 m，达到规范规定的精度要求。

图4 试件拉伸破坏形态图Fig.4 Tensile failure diagram of specimen

试件的屈服强度是根据每个试件在不同腐蚀情况下，通过拉伸试验测量得出的真实屈服强度。根据拉伸试验结果，得到腐蚀损失率与屈服强度以及屈服荷载之间的关系，如图5和图6所示。

图5 腐蚀损失率与屈服强度关系Fig.5 The relation between corrosion loss rate and yield strength

图5曲线具有明显的离散性，而图6具有明显的下降趋势。由图5和图6分析可得，在腐蚀损失率在22%范围内，随着腐蚀损失率的增大，构件的屈服荷载逐渐降低，但屈服强度与腐蚀损失率的相关程度较低。

图6 腐蚀损失率与屈服荷载关系Fig.6 The corrosion loss rates eta relationship with yield load

图7与图8为试验测定的试件腐蚀坑最大深宽比与试件的屈服强度、腐蚀坑最大深宽比与极限强度的关系。试件截取选用的管道钢腐蚀条件基本相同，各试件腐蚀坑的最大深宽比多集中在0.06附近。但随着最大深宽比的增大，屈服强度和极限强度均明显减小，这与表面腐蚀坑引起的应力集中导致的钢材强度退化有关。

图7 最大深宽比与屈服强度关系Fig.7 The relation between maximum depth-width ratio and yield strength

图8 最大深宽比与极限强度关系Fig.8 The relation between maximum depth-width ratio and ultimate strength

为了分析腐蚀钢材的力学性能，引入等效弹性模量，该等效弹性模量是指按结构的真实屈服承载力计算的弹性模量。定义试件的等效弹性模量Ee[14]如下式所示。

(2)

式中：py为坑蚀管道钢试件的屈服承载力；ΔL为试件沿长度方向的变形量；A为试件面积。

如图9和图10所示，等效弹性模量随腐蚀损失率的增加而减小，而弹性模量与腐蚀损失率的相关度小。

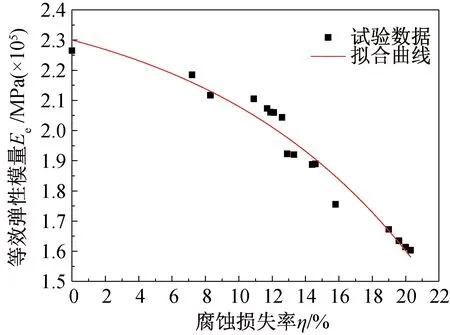
图9 腐蚀损失率与等效弹性模量关系Fig.9 The relation between corrosion loss rate and equivalent elastic modulus

图10 腐蚀损失率与弹性模量关系Fig.10 The relation between corrosion loss rate and elastic modulus

为了分析等效弹性模量与材料弹性模量之间的关系，引入等效弹性模量与弹性模量的比值ζ，按照公式(3)计算并建立η-ζ关系，如图11所示。

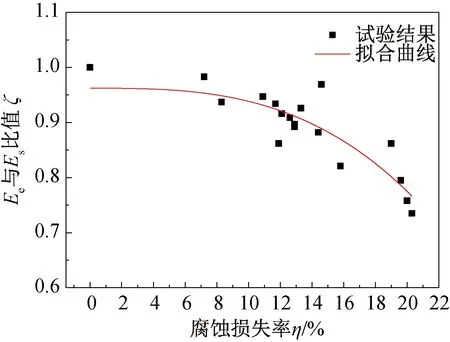
图11 η-ζ关系曲线Fig.11 η-ζ relation curve

(3)

利用“L-M”(Levenberg-Marquardt)算法将试验数据进行拟合并建立η-ζ非线性经验公式，如公式(4)所示。

ζ′=0.46+0.54e-η1.4/124

(4)

式中，ζ′是基于公式计算得到的等效弹性模量与弹性模量的比值。

将等效弹性模量Ee作为材料的弹性模量，用于分析带腐蚀缺陷管道钢的力学性能，则有Ee与Es之间的近似计算公式如(5)所示。

(5)

利用公式可推算出含腐蚀缺陷管钢的等效弹性模量，只需测定腐蚀损失率，即可推出不同腐蚀缺陷的管钢在拉压作用下的力与变形关系。计算结果与试验值计算结果对比，公式计算结果与试验值基本吻合，如图12所示。

图12 Ee分析结果对比Fig.12 Comparison of Ee analysis results

2 管钢腐蚀坑处应力状态有限元分析

2.1 应力集中系数Kt

在拉力作用下，带腐蚀缺陷的管钢在腐蚀坑处易产生应力集中现象，使管钢过早屈服或断裂。Cerit 等[5]利用有限元分析方法对应力集中问题进行研究，建立了一系列三维半椭圆点状腐蚀模型，系统地研究了在单轴拉伸作用下半椭圆形腐蚀坑处的应力分布情况，得出了腐蚀坑深宽比是影响应力集中系数的主要因素，并提出了应力集中系数Kt的计算式如公式(6)所示。

(6)

式中：d为腐蚀坑的深度，ω为半椭圆形腐蚀坑的宽度，垂直于受力方向的尺寸。

2.2 有限元模型的建立

利用ABAQUS有限元分析软件，建立带腐蚀缺陷管钢分析模型(图13)。分析中使用的实体模型尺寸同试验试件尺寸，腐蚀坑采用三维半球形腐蚀坑，腐蚀坑深宽比根据试验测得的βmax值进行确定。在临界截面上，腐蚀坑处的应力集中系数Kt，通过使用由横截面面积确定的最大名义应力σs,max与未开孔的标准名义应力σs的比值来计算确定。由于坑的宽度ω远小于构件的尺寸，在计算净面积时可忽略不计。

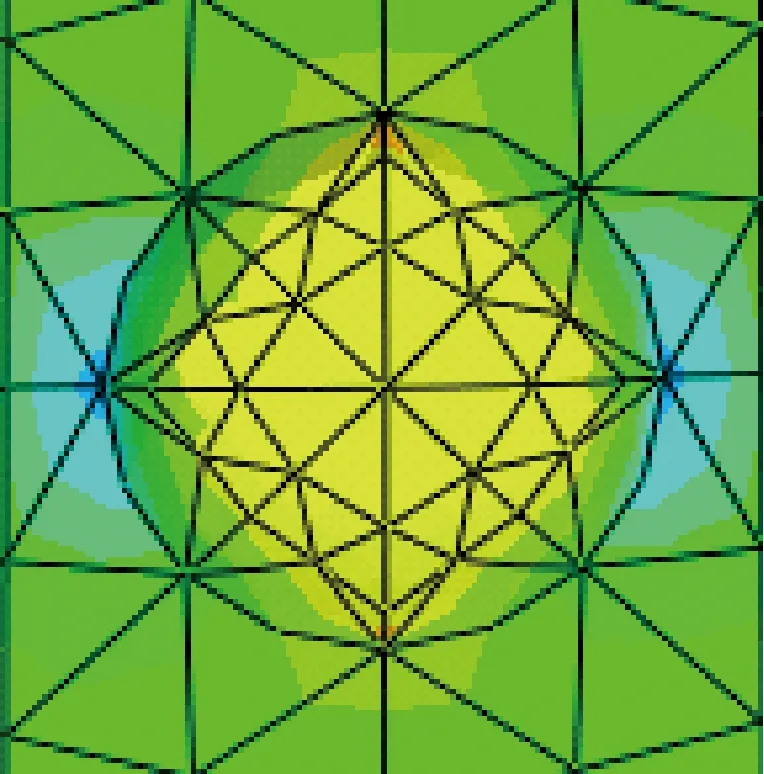
图13 管钢腐蚀缺陷处有限元分析模型Fig.13 Finite element analysis model of corrosion defect of pipe steel

2.3 有限元结果分析

根据上述要求建立不同深宽比腐蚀坑处的应力分析模型。对带腐蚀缺陷的管钢试件进行全截面拉伸，分析管钢试件腐蚀坑处应力状态。

根据公式(6)和有限元分析计算出各试件腐蚀坑处的应力集中系数，如表2所示。从表2中数值可以看出，腐蚀坑处的应力集中系数随着最大深宽比的增加而增大。公式法和有限元分析得到的应力集中系数Kt基本一致，误差在10%以内。

表2 管钢试件腐蚀坑处应力集中系数Tab.2 Corrosion coefficient of steel pit at test tube

3 结论

1) 通过对含腐蚀缺陷的管钢进行拉伸试验，发现随着腐蚀损失率的增大，断裂位置由试件中间向两侧离散性发展，且其断裂位置一般发生在腐蚀坑最大深宽比处。含腐蚀缺陷的管钢随着腐蚀程度(腐蚀损失率22%以内)的增加，其屈服强度、弹性模量与腐蚀损失率的相关度较低，而屈服荷载和等效弹性模量随着腐蚀程度的增加而明显降低。

2)根据试验得到的等效弹性模量Ee与弹性模量Es的比值ζ，利用“L-M”算法建立ζ′与腐蚀损失率η之间的表达式，并且与试验结果相对比，得出公式计算结果与试验值基本吻合，利用该公式可推算出腐蚀缺陷管钢等效弹性模量。

3)腐蚀管道钢的屈服强度、极限强度与腐蚀坑最大深宽比有较大关系，随着最大深宽比的增大，屈服强度和极限强度均明显减小，这与表面腐蚀坑引起的应力集中所导致钢材的强度退化有关。利用软件模拟计算出的应力集中系数结果与利用公式计算出的结果基本一致，并且管钢腐蚀坑处的应力集中系数与腐蚀坑最大深宽比基本同幅度增大。