底部加强双钢板混凝土组合剪力墙抗震性能研究

袁朝庆，代晓辉，宋 爽，李国洋，房宽光，计 静

(东北石油大学 土木建筑工程学院，黑龙江 大庆 163318)

目前随着社会经济高速发展，商业用地较为紧张，为了提高土地利用率出现越来越多的高层及超高层建筑。剪力墙构件是超高层及高层建筑中主要抗侧力构件之一[1-2]，因此本文主要对剪力墙构件展开研究。对于传统的钢筋混凝土剪力墙(Reinforced Concrete Shear Wall，RCSW)，其作为主要抗侧力构件，在地震中广泛应用[3-5]。但RCSW存在明显的不足，如自重较大；混凝土容易产生裂缝，延性较差；工期相对较长。为了弥补这些不足，钢板混凝土组合剪力墙应运而生，钢板混凝土组合剪力墙有着较强的耗能能力和延性[6-7]。特别是双钢板混凝土组合剪力墙重量较轻、强度较高，充分发挥了钢板和混凝土的优势。双钢板混凝土组合剪力墙最初应用于海底隧道和核电工程等领域，逐渐应用到高层及超高层建筑结构领域。虽然双钢板混凝土组合剪力墙结构得到了明显的改善，但也有不足。双钢板混凝土组合剪力墙在循环往复荷载作用下，双钢板混凝土组合剪力墙底部最容易发生屈曲。国内外学者对其端部引入了方钢管边缘柱构件，延性和耗能能力均有所提升。纪晓东[8]、武晓东[9]分别对端柱方钢管内配圆钢管试件的抗震性能展开试验研究，纪晓东试验结果表明，相比普通试件，内配圆钢管试件的耗能能力和承载能力均有所提高。武晓东设计的端部内配圆钢管试件全部发生压弯破坏，塑性变形能力较好。

目前对试件底部加强的研究较少，张鹏[10]设计了9个底部加强试件，通过改变底部尺寸的方式，进行底部加强。研究结果表明，墙体的承载能力、延性及耗能能力均有提高。随着底部加强区的高度，底部屈曲位置上移。目前国内外没有对于将工字型钢加入双钢板混凝土组合剪力墙底部的研究。本文在双钢板混凝土组合剪力墙底部不同位置设置了型钢，研究型钢数量、型钢强度、钢板强度、型钢尺寸和轴压比对双钢板混凝土组合剪力墙抗震性能的影响。

1 有限元模型建立

1.1 材料本构选取

钢板、方钢管和型钢本构关系，均采用理想的四折线本构关系，金属塑性模型。钢材材料选用Q235钢和Q345钢。常温静载状态下，钢材的单向拉伸的应力应变曲线如图1(a)所示，混凝土本构关系采用韩林海[11]的本构关系，如图1(b)所示塑性损伤模型，混凝土材料选用C40。

图1 材料本构关系Fig.1 Constitutive relation of material

混凝土受压本构关系表达式为：

(1)

式中：x=ε/ε0，ε0=εc+800ξ0.2×10-6，εc=(1 300+12.5fc88)×10-6；y=σ/σ0；

混凝土受拉本构关系表达式为：

(2)

式中：x=ε/ε0；y=σ/σ0；δp=0.26×(1.25fc)2/3；εp=43.1δp。其他物理量意义见文献[11]。

1.2 单元选取与接触关系

本文分析模块采用的是ABAQUS/Standard，混凝土、方钢管、型钢、钢板和栓钉均选用C3D8R实体单元。混凝土与钢材的接触方式定义为表面与表面接触，钢材与混凝土的关系为粘结滑移，混凝土和钢材的法向接触为“硬接触”，切向接触为“罚”接触，摩擦系数设置为0.6。

1.3 加载方式与边界条件

模型计算分析步设置step1和step2，初始状态，试件的底部边界条件设置为完全固定，顶部为自由。在剪力墙顶面设置参考点与顶面耦合，step1时在顶部耦合点施加恒力荷载，分析步step2时在顶部耦合点施加水平位移循环往复荷载，加载制度如图2所示。

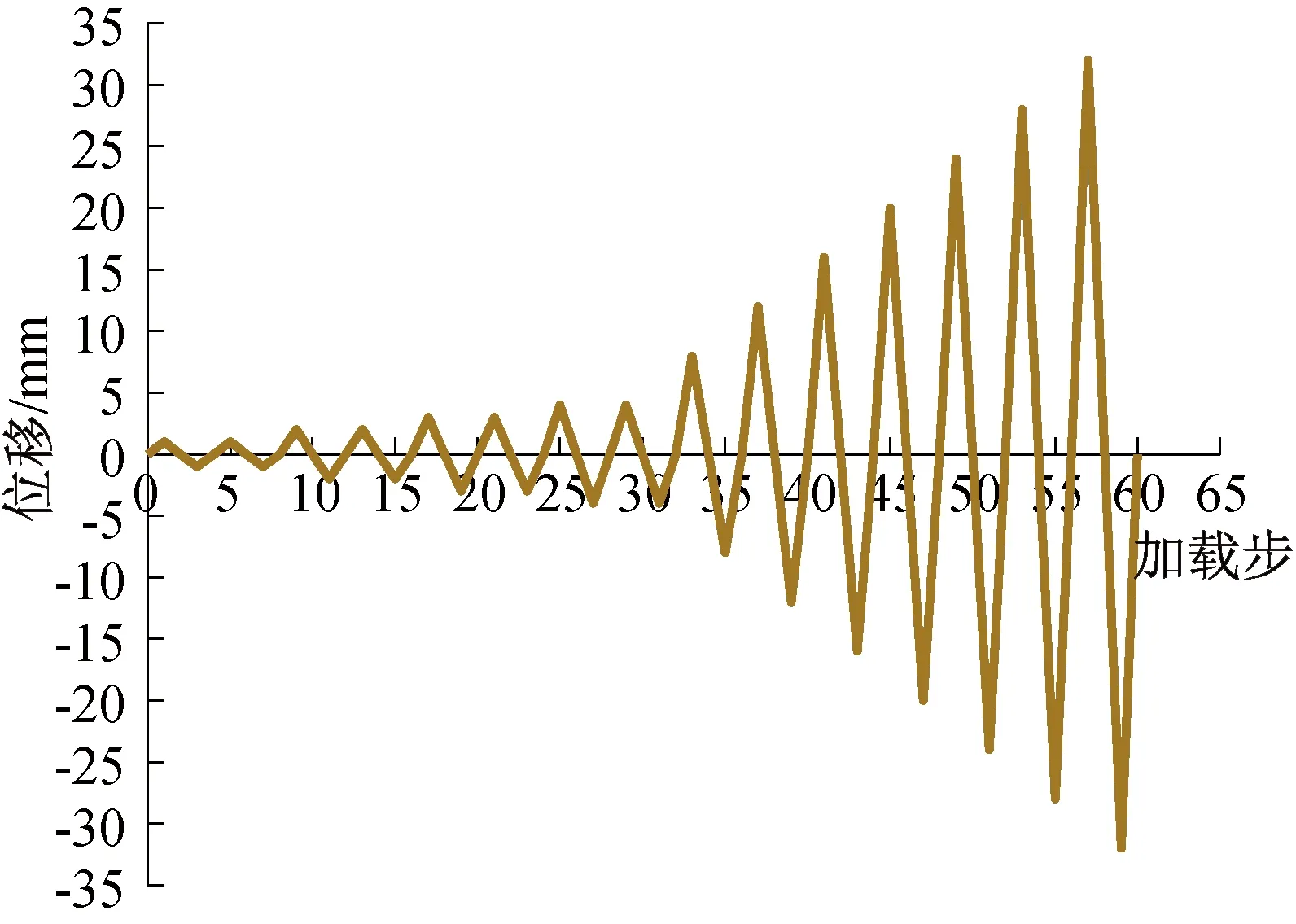
图2 加载制度Fig.2 Loading system

2 有限元模型对比验证

本文以文献[12]中的双钢板剪力墙试件DCSW1的拟静力试验为例，对其进行有限元模拟，从而验证有限元模型的可行性。本文建立的双钢板剪力墙模型DCSW1#与文献[12]中的模型DCSW1尺寸相同，有限元模型如图3所示。有限元破坏模式和试验所得的破坏形态一致，如图4所示。

图3 验证模型示意图Fig.3 Schematic diagram of the validation model

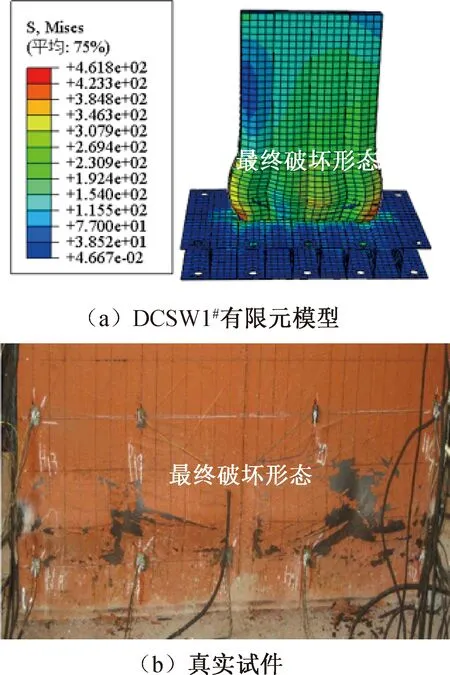
图4 破坏形态对比Fig.4 Comparison of failure modes

图5是骨架曲线，图6(a)、(b)分别为文献的试验试件DCSW1和本文的验证模型DCSW1#的滞回曲线，由图5和图6可以看出：两条骨架曲线形状相同，有限元模拟的骨架曲线DCSW1#与试验的骨架曲线相似。由滞回曲线图可以看出，试验的带回曲线和本文验证的滞回曲线接近一致，有限元模拟情况下的滞回曲线更加光滑饱满。由表1可知，最大误差为8.32%，可以认为ABAQUS能较好地模拟双钢板剪力墙在往复荷载作用下的抗震性能。

图5 骨架曲线对比Fig.5 Comparison of skleton curves

图6 滞回曲线图Fig.6 Hysteresis curve

表1 试验结果与有限元结果对比Tab.1 Comparison of test results and finite element results

3 端部加强双钢板混凝土组合剪力墙抗震性能研究

3.1 试件设计

本文设计了1个底部不加强试件，8个底部加强试件，如表2所示，试件的有限元模型示意图如图7所示，模型构造示意图如图8所示，分别对其滞回曲线、骨架曲线、承载能力、延性、耗能能力进行对比分析，研究其相关规律。

图8 模型构造示意图Fig.8 Schematic representation of the mode construction

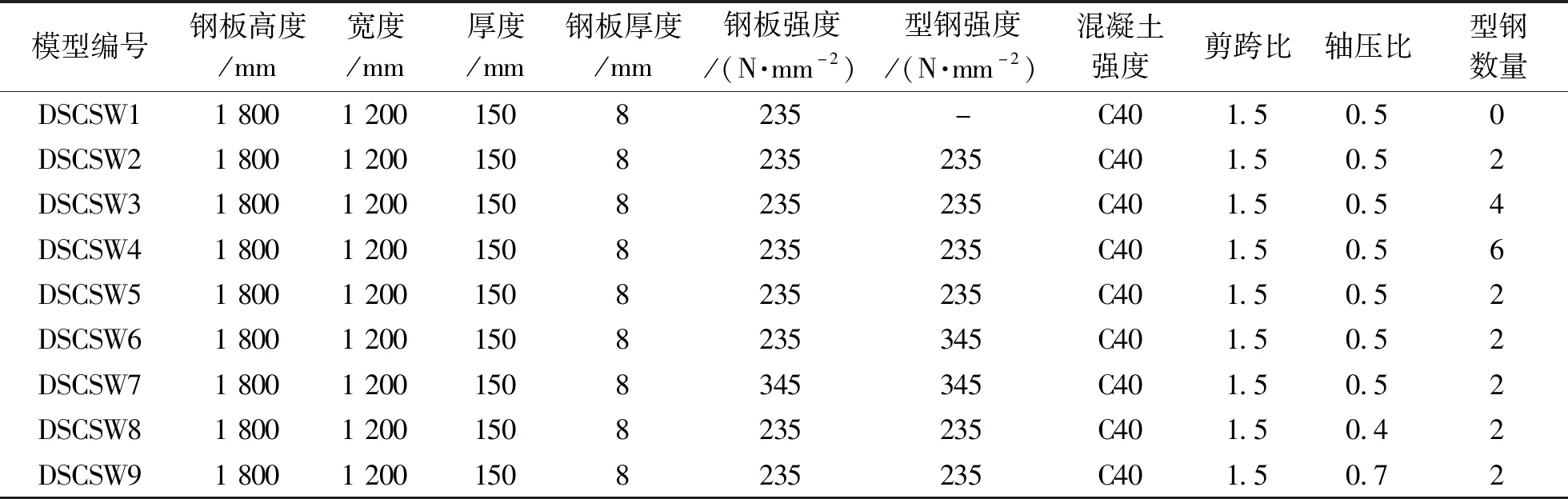
表2 试件参数Tab.2 Parameters of test specimens

图7 有限元模型示意图Fig.7 Schematic representation of the finite element model

3.2 荷载-位移曲线分析

3.2.1 滞回曲线分析

图9为9片DSCSW试件的滞回曲线，由图9可知，底部配置型钢对试件的P-Δ曲线影响效果显著。由图9(a)、(b)可知，底部配置型钢，滞回环更加饱满，极限位移增大，塑性变性能力增强，且随着水平位移增大，水平荷载的下降速率逐渐缓慢。图9(b)—(f)可知，改变型钢数量、型钢强度和型钢尺寸，对试件影响不显著。由图9(a)、(e)、(g)可知，提高钢板和型钢强度，极大地提高了滞回环饱满程度和峰值荷载，极限位移增大，塑性变性能力增强。图9(d)、(h)、(i)可知，轴压比为0.4和轴压比0.5试件滞回环相近，轴压比为0.7的试件峰值荷载下降，极限位移下降，塑性变形能力下降，延性降低。

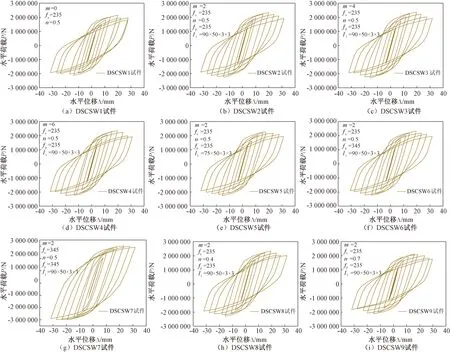
图9 滞回曲线Fig.9 Hysteretic curve

3.2.2 骨架曲线分析

图10为9片底部加强试件的骨架曲线，各组试件骨架曲线均呈倒S形，试件破坏可以分为弹性、塑性和破坏阶段。加载初期，各组试件的骨架曲线接近重合，此时试件处于弹性阶段，试件达到峰值以后，试件卸载不可完全恢复。由图10(a)可知，底部加入型钢的试件相比底部不加强试件，提高了承载能力，极限位移增大，骨架曲线下降段愈发平缓，延性较好，型钢的数量对试件影响并不显著。由图10(b)、(c)可知，型钢的尺寸和强度对底部加强试件影响不显著，但可以看出，型钢尺寸较小的试件提前进入下降段，延性相对较差。由图10(d)可知，轴压比为0.4和0.5试件峰值荷载和屈服荷载接近，轴压比为0.7试件相比轴压比为0.4和0.5试件，峰值荷载有所下降，且下降段愈发陡峭，延性降低。由图10(e)可知，钢板强度和型钢强度提高，峰值荷载有所提高，下降段趋于平缓，延性较好。

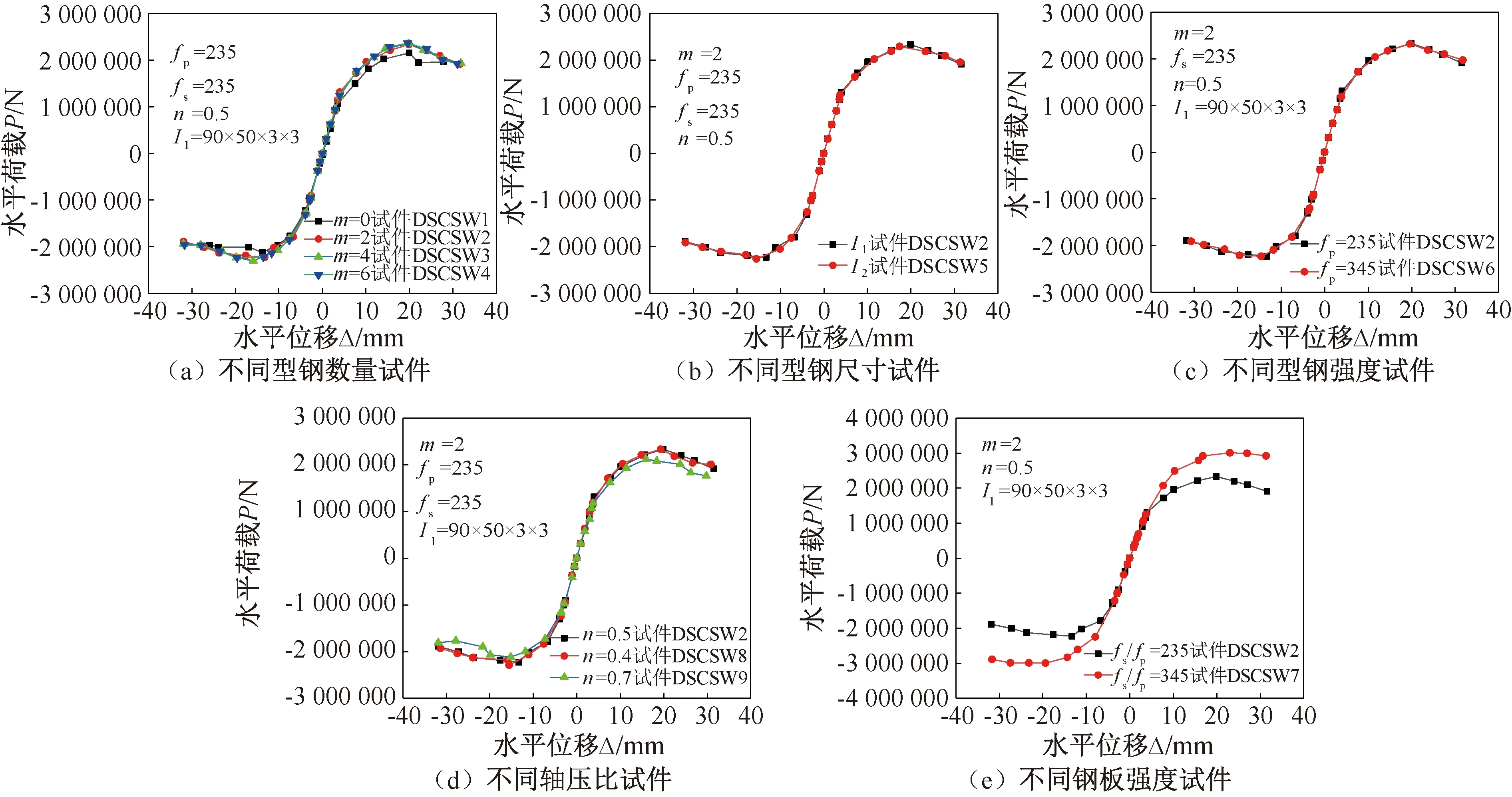
图10 骨架曲线Fig.10 Skeleton curve

3.3 承载能力对比分析

结构承载能力是评价结构强度和结构抗震性能的重要指标之一，本文采用“割线刚度法”，达到85%的峰值荷载即达到极限荷载，视为破坏，如公式(3)所示。各组构件的屈服荷载、峰值荷载、极限荷载值大小可见表3。

pu=0.85pm

(3)

由表3可知，底部加入型钢试件的屈服荷载、峰值荷载和极限荷载均有所提高。屈服荷载方面分别提升了1.27%、8.08%、8.60%、0.87%、3.25%、34.44%、5.46%、1.39%，峰值荷载分别提升了5.19%、8.49%、10.38%、6.60%、5.19%、41.04%、8.02%、9.43%。可以看出，随着型钢数量的增加，屈服荷载和峰值荷载在逐渐增加。提高型钢强度和钢板强度，屈服荷载均有提升，屈服荷载最大提升了34.44%、峰值荷载最大提升了41.04%。

表3 各模型承载力特征点的有限元结果Tab.3 Finite element results of characteristic points of bearing capacity of each model

3.4 变形与延性分析

构件在发生屈服后，在满足承载力要求下的良好塑性变形能力称为延性。延性的具体求出方法按照极限位移与屈服位移之比，即公式(4)：

(4)

式中：Δu为极限位移，Δx为屈服位移，β为延性。

通过DSCSW系列模型提取计算出具体位移参数和延性参数如表4所示。

由表4可知，底部加入型钢的试件相比普通试件，延性有较大提高。延性分别提高了19.08%、14.13%、15.19%、9.89%、12.72%、21.55%、14.84%、9.54%。由DSCSW2—DSCSW4可知，在轴压比为0.5时，m=2的试件延性提高程度最大。型钢尺寸对延性影响较大，减小型钢尺寸，延性降低。在轴压比0.5时，提高型钢强度和钢板强度，延性提高程度很高。轴压比为0.4和0.5，延性相近，轴压比为0.7时，延性降低。

表4 各模型变形能力计算的有限元结果Tab.4 Finite element results of the deformation capacity of each model

3.5 刚度退化能力分析

刚度退化曲线是指滞回曲线每次循环加载的峰值荷载点与峰值位移的比值按照加载级别顺序连接的曲线。对于双钢板混凝土组合剪力墙在往复荷载作用下抵抗变形的能力，本文采用公式(5)分析了DSCSW系列模型的刚度退化关系。

(5)

式中：pi等于第i次循环的峰值荷载，Δi为第i加载对应的峰值位移。

由图11(a)可以看出，底部加强的试件相比普通试件，整体刚度均有所提高，且刚度退化速度较慢，滞回曲线较为稳定，耗能能力较好。由图11(b)可知，提高型钢和钢板强度，整体刚度有较大提升。由图11(c)可知，轴压比对试件刚度退化速度影响不大，刚度退化速度接近一致。

图11 刚度退化曲线Fig.11 Skeleton degradation curve

3.6 耗能能力分析

等效粘滞系数、能量耗散系数和累积耗能均能反映组合剪力墙的耗能能力。本文选用等效粘滞系数来定量地分析带型钢暗柱双钢板混凝土组合剪力墙的耗能能力，等效粘滞系数越大，剪力墙在往复荷载下产生的滞变阻尼越大，剪力墙的耗能能力越好，即地震作用下的安全性更加优良，其计算简图12和公式(6)如下：

图12 等效粘滞系数示意图Fig.12 Schematic diagram of the equivalent viscosity coefficient

(6)

图13为各组试件的等效粘滞系数对比图，由图可知，各组试件的等效粘滞系数随着层间位移角的增加，快速增长至峰值而后平缓。由图13(a)可知，随着层间位移角的增加，底部加强试件的等效粘滞系数要高于普通试件，在轴压比为0.5时，型钢数量增加，对等效粘滞系数的峰值影响并不显著。由图13(b)可知，提高型钢强度，等效粘滞系数增大，提高钢板和型钢强度，等效粘滞系数的峰值极大增加，提高了试件的耗能能力。由图13(c)可知，轴压比为0.4和0.5试件的等效粘滞系数接近重合，轴压比为0.7试件的等效粘滞系数有所提高。

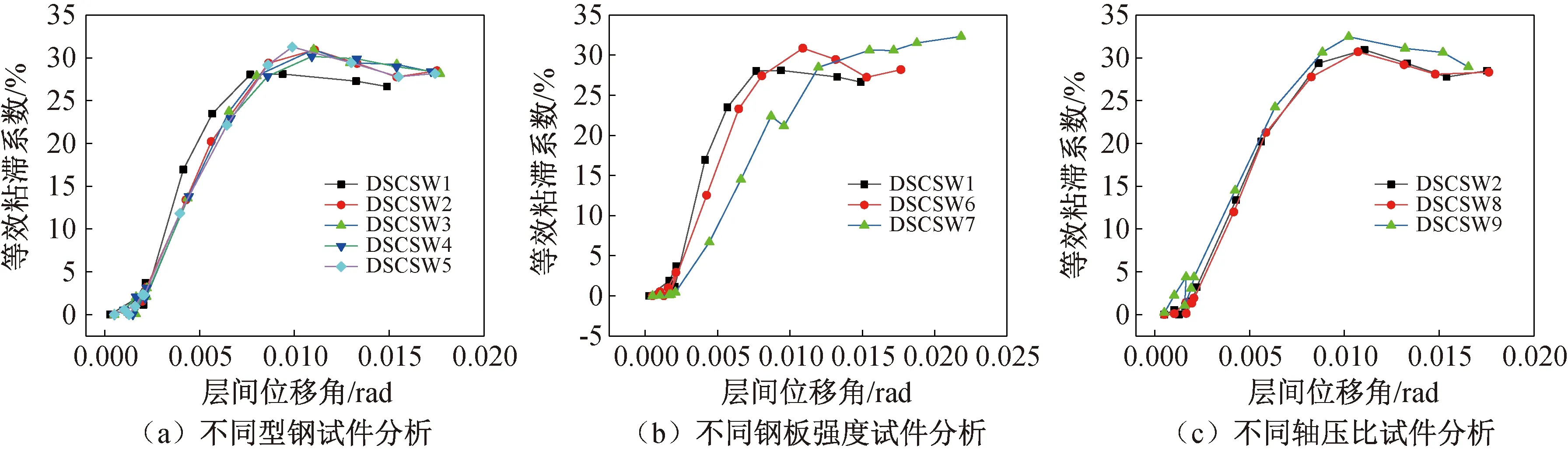
图13 等效粘滞系数对比Fig.13 Schematic diagram of the equivalent viscosity coefficient

4 结论

1)底部加强试件在承载能力、延性、塑性变性能力、刚度退化和耗能能力方面均有所提升，承载能力方面，屈服荷载提升幅度达到了34.44%、峰值荷载提升幅度达到了41.04%，延性方面提升了21.55%。

2)试件底部型钢数量对承载能力影响显著，通过9片试件相比较，可以得出，底部加型钢试件随着型钢数量的增加，承载能力逐渐提高。但底部型钢的数量对延性、耗能能力、刚度退化能力影响并不显著。对于提高钢板和型钢强度，试件的延性、初始刚度和耗能能力均有较大提升，可以看出，底部加型钢试件相比底部不加型钢试件抗震性能较优。

3)轴压比对试件的延性影响显著，在轴压比0.5时，提高型钢强度和钢板强度，延性提高程度较大。轴压比为0.4和0.5，延性相近，轴压比为0.7时，延性降低。但轴压比对初始刚度和耗能能力影响并不显著。