基于换道概率分布的多车道交织区元胞自动机模型

谢济铭，彭博，秦雅琴*

(1.昆明理工大学，交通工程学院，昆明 650500；2.重庆交通大学，交通运输学院，重庆 400074)

0 引言

在城市道路网络中，快速路衔接城际高速公路与城市内部道路，承担城市中大量、长距离和快速交通服务，已成为国内众多大中城市交通运行体系的重要组成部分。交织区是快速路系统的关键部位，其交通流特性比较复杂，国内外学者对其展开了较多研究。探析了交织区流量、密度、速度及通行能力等中宏观交通流特性，有助于提高交织区的交通运行效率。

从更微观的视角而言，交织区车辆频繁换道、相互冲突和干扰加剧，频繁复杂的换道行为使交织区呈现出特殊的交通流特性。因此，研究交织区车辆换道行为规律并进行有效建模是探明交织区交通运行机理的关键和基础。一些学者尝试建立交织区换道逻辑，模拟整个过程中的加减速及换道行为[1]。此外，还有学者考虑到车辆换道行为受驾驶员心理影响[2]及车辆换道时会对汇入汇出位置、安全间隙等融合序列决策[3]，动态模拟交通条件变化对合流车辆定位间隙的选择和合流策略的影响。

受限于换道需求及道路条件等实际约束，交织区及其附近的车辆跟车间距较小、换道行为频繁，而距离较远的上下游区段没有汇入或汇出主线的迫切需求，体现为交织区中段或末端换道较为集中，而其他位置换道次数较少。因此，交织区车辆在不同位置的换道需求强度与换道行为有明显差异，但既有文献较少专门研究这种差异性[4-5]。部分学者针对基本路段探索了换道概率对交通流的影响[6]，对于交织区车辆换道建模分析有一定借鉴价值。交织区换道行为需要大量车辆微观轨迹数据作为支撑，一些学者利用驾驶模拟器[7]或实车测试[8]提取数据展开研究，不过较难获得交织区全样本车辆轨迹，难以掌握车辆换道动态交互特性。

2006年，美国联邦公路局公开了时长约60 min的高速公路交织区与城市干道交叉口全样本车辆微观轨迹数据集NGSIM，此后至今，国内外许多研究均基于NGSIM 展开车辆跟驰与换道等研究[3,5]，然而由于道路条件、交通规则及文化差异，NGSIM难以反映国人真实驾驶行为特征。

元胞自动机作为一种离散性微观模型，关注交通流中个体车辆的运动状态，可以自定义车辆运动规则、适应各种实际的交通流环境，在交织区乃至基本路段交通流研究中应用十分广泛[1,2,5,6,9]。为细致刻画交织区复杂的车辆换道行为，本文针对多车道交织区，利用无人机拍摄高空视频提取高分辨率车辆微观轨迹数据，分析车辆速度、加速度、换道行为等时空分布特征。考虑换道需求强度与换道行为差异性，提出交织区动态换道概率分布模型，建立基于路径转换需求、动态安全间距与动态换道概率等要素的交织区元胞自动机交通流模型，并进行实测分析与模型对比验证。

1 数据采集与分析

1.1 数据采集

针对交织区及其影响区域为研究对象，进行观测实验，获取车辆运行数据，分析和研究交通运行特性。由于同侧-匝道交织区能被交织车辆使用的最大车道数是最受限制的，可供交织车辆使用的车道数最多为1.4车道，即便实行了限货限摩管制，但在高峰时段此类型交织区车辆行驶行为仍比较混乱。

因此，本文选取重庆市某同侧-匝道型交织区进行数据采集，此交织区车道数量较多、交织距离较短、承担多个组团间车流转化的功能，如图1所示。该交织区承担东西流向主要过境流量，主线4条车道、匝道2 条车道，车辆速度离散、行为随机、冲突集聚，体现出独特的交通特性。为精细捕捉该交织区车辆换道复杂特性，在天气良好的工作日，利用无人机悬停于交织区上方120 m 采集车辆运行高清视频。在实验过程中，为避免数据采集影响交通运行，要求实验人员在人行道或周边高地，使用无人机装置录制高清视频数据。

图1 高空视频拍摄场景Fig.1 High-altitude video shooting scene

为有效获取交织区车辆运行微观信息，课题组基于OPEN CV 自主开发多尺度KCF(Kernerlized Correlation Filter)车辆跟踪优化算法，从航拍视角对运动车辆进行自动识别和跟踪，对数据进行坐标变换、数据验证和误差消除等处理分析[10]，得到帧ID、时间ID、车辆ID、车辆质心坐标等车辆动态属性。

通过车辆自动跟踪及人工标定，得到行经交织区车辆完整样本2912个，共计110余万条微观轨迹数据。经验证，轨迹信息自动跟踪算法空间位置误差仅为3.32%，误差均值为-0.39 km·h-1(-0.11 m·s-1)。25%分位数误差值约为-2.3 km·h-1(-0.64 m·s-1)，75%分位误差值约为1.4 km·h-1(-0.39 m·s-1)，时间分辨率0.1 s(10 Hz)、空间分辨率0.1 m·px-1(10 cm)，数据颗粒度小，检测结果精度较高，为车辆换道行为模型的构建及验证提供数据支撑。

车辆换道信息提取过程如图2所示，在路缘线上设置虚拟线圈检测器，每隔1 m 布置一个检测器，车辆每跨越一次车道，5个线圈记录一次换道数据。车辆换道方向根据车辆轨迹的1阶导求得，同时，由行进方向与路缘线间的角度阈值，筛选压线行驶等异常行为。

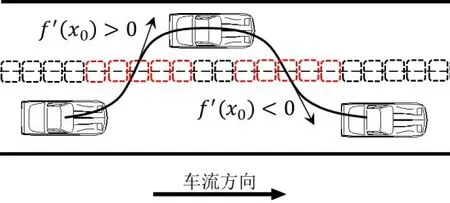
图2 换道信息采集示意Fig.2 Channel change information collection schematic

1.2 运行特性分析

交织区主要承担主线与匝道车流相互转换的功能，其中最内侧车道为定向车道、最外侧车道为匝道2，基本无车辆换道行为，本文对此不展开研究。观测发现，为尽快汇入目标车流，一些车辆在交织区上游附近提前换道，更多车辆需在交织区换道。因此，在交织区及其紧邻上下游一段范围内，车辆跟车间距较小、急加减速及换道行为较频繁；而距离交织区更远的上游和下游区段，没有汇入或汇出主线的迫切需求，跟驰和换道自由度较大，车辆行驶行为特性与基本路段相近。

统计交织区及紧邻上下游每个换道点的换道频率，其散点及高斯拟合曲线如图3所示，可看出，所有方向的换道频率分布基本呈Gaussian分布，换道行为集中在交织区(40～160 m)。图3(a)和图5(b)为主线换道频率分布，主线内侧换至外侧峰中心位置偏左，而主线外侧换至内侧峰中心位置偏右，说明进入交织区前，内侧车道的车辆倾向于提前变换车道，而外侧车道的车辆多在交织区中后段才能汇入内侧车道。图3(c)和图3(d)为主线与匝道间换道频率分布曲线呈双峰分布形态，交织区中段车辆换道行为最集中，而在交织区末端也形成了换道小高峰，表明交织区换道强度较高，一些途中未成功换道的车辆只能在交织区末端汇入主线，可能冒着较高的安全风险进行换道。

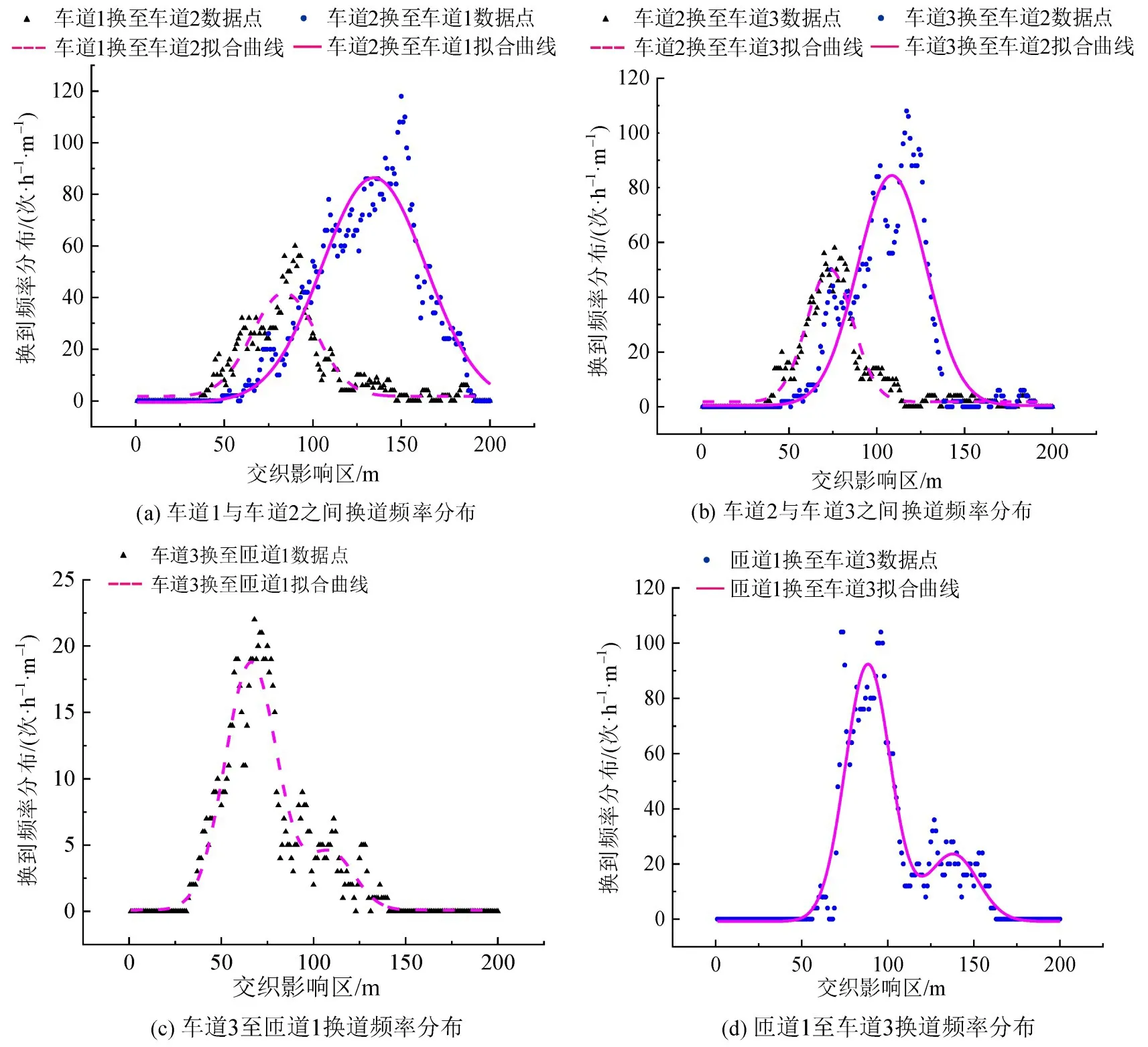
图3 交织影响区6个方向换道频率分布Fig.3 Lane changing frequency distribution of six directions in weaving impacted area

2 模型构建

2.1 模型简介

考虑车辆行为及几何条件等差异性，将交织区研究范围划分为3个区段，如图4所示。①换道决策几乎不受交织区影响的上、下游；②交织影响区，换道决策受交织区影响较明显，覆盖了交织区及两端一定长度的延伸区段。

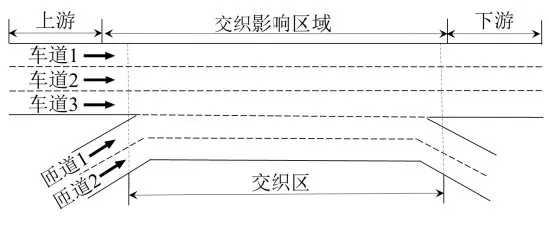
图4 多车道交织区研究范围Fig.4 Research scope of multi-lane weaving area

2.2 上下游换道模型

如图5所示，在上下游路段，处于车道i的第j辆车，根据t时刻本车(i,j)与邻近车辆(i±1,j±1)的速度v(·)及间距g(·)判断换道条件，执行换道行为。换道过程包括生成换道动机、判断换道间距条件、动态换道概率判断、目标车道后车速度同步更新。

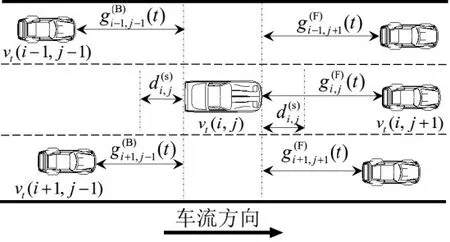
图5 换道主要影响因素Fig.5 Main impact factors when changing lanes

2.2.1 换道动机规则

引入Gipps 紧急制动间距模型，当车辆(i,j)车前间距较小时，可能与前车追尾，此时考虑动态行车安全间距及停车安全间距，产生换道动机。如果满足

则产生换道动机，进入2.2.2节。

2.2.2 换道间距规则

根据停车安全间距，判断车辆与目标车道邻近车辆间距是否满足换道的安全要求，若满足，则进入2.2.3节。安全要求为

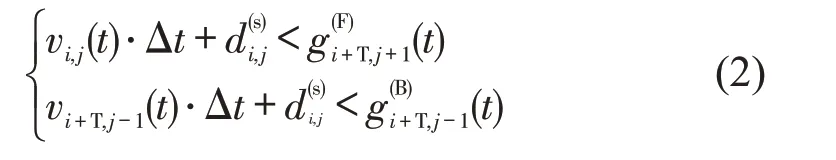
式中：Δt为时间步长；vi+T,j-1(t)为t时刻邻道上的后车速度；为本车与邻道前车的间距；为邻道后车与本车的间距；T为车辆换道方向参数，向左换道时T=-1，向右换道时T=1。

2.2.3 换道概率规则

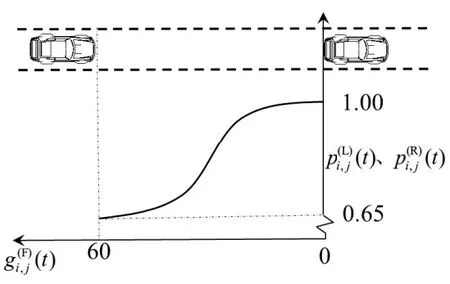
图6 Logistic曲线换道概率Fig.6 Logistic curve lane change probability

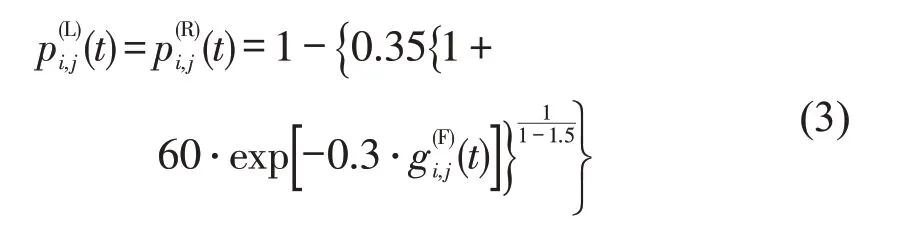
2.2.4 目标车道后车速度同步更新

考虑车辆(i,j)换道时与目标车道后车(i+T,j-1)的间距和速度差，(i+T,j-1)需在(i,j)换道时同步更新速度以满足安全要求。该规则在换道时同步更新后车速度，以充分描述换道对后车乃至交通流的干扰。

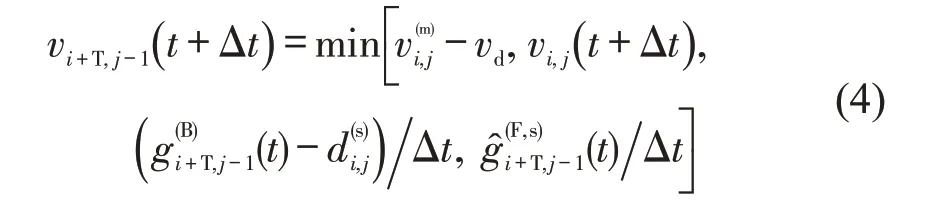
2.3 交织影响区换道模型

对于多车道交织区，车辆需在有限距离内换至目标车道，换道条件局促、换道行为频繁。车辆为了汇入主线或驶入匝道，可能采取减速、低速甚至停车换道等风险较高的驾驶行为，以增加换道决策机会及成功换道几率。为有效描述交织区复杂的换道行为机理与决策过程，考虑换道需求、动态行车安全间距、停车安全间距及动态换道概率等因素，构建交织影响区多级换道决策模型，包括换道动机判断、换道时机决策及换道概率决策。

2.3.1 换道动机规则

相比上下游区域，车辆在交织影响区的换道动机更加复杂，除了寻求更快的通行速度与更大的行驶空间外，还具有汇入汇出主线的路径转换需求。因此，在换道动机规则中，增加考虑了汇入主线和驶入匝道的需求因素。使用φ1表示主线向匝道的车辆汇入比，φ2表示匝道向主线的车辆汇入比，r(0,1)表示0～1间随机数。

如果满足

产生换道动机，进入2.3.2节。

如果满足

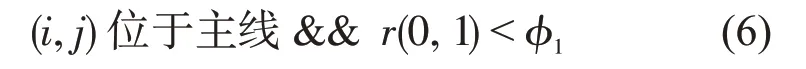
产生驶入匝道需求动机，进入2.3.2

否则

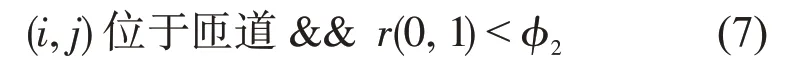
则产生汇入主线需求动机，进入2.3.2

2.3.2 换道时机规则

为模拟车辆在交织区影响区的复杂换道决策行为，在挖掘分析实验数据的基础上，建立了考虑车辆速度、间距和停车安全间距等主要因素，以低风险换道为目标的换道时机逐步决策规则[5]。根据车速和间距关系及安全风险，可分为5 类换道情形。这5种情况的换道强度及安全风险逐渐增加，通过逐步决策选择换道时机。

2.3.3 换道概率分布建模

根据1.2 节交织影响区换道频率分布散点图，建立高斯曲线拟合方程为

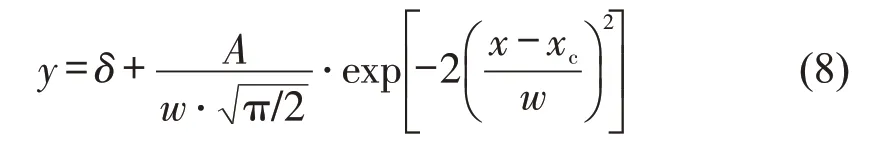
式中：δ为偏移量；x为换道频率位置，即车辆在交织影响区换道空间位置；xc为峰中心位置；w为高斯峰的半高宽；A为峰面积。各换道方向的调节系数与假设检验结果如表1所示。

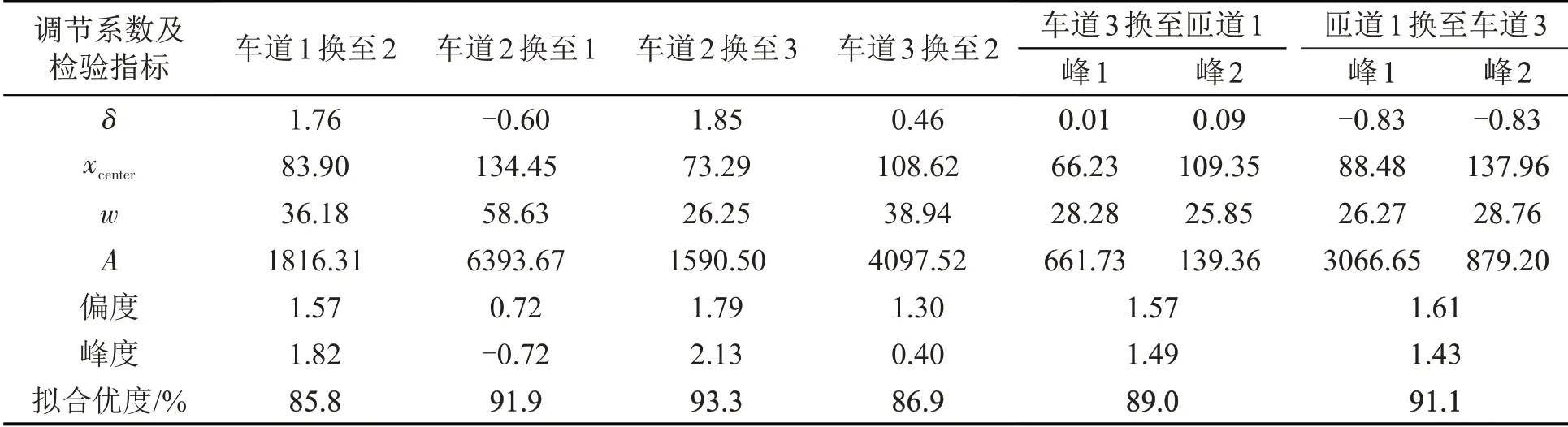
表1 高斯拟合系数与检验Table 1 Gauss fitting coefficients and test

由表1可以看出，所有样本偏度绝对值小于3，峰度绝对值小于10，换道频率基本服从Gaussian分布[11]。据此，建立换道概率Gaussian 分布模型H(x)为

式中：Hs(x)为单峰分布；Hd(x)为双峰分布；a1为函数在纵向偏移量；为峰值极限值；为横向偏移量；为分布曲线形状参数。

2.3.4 换道概率规则

当车辆(i,j)运行至交织影响区车道i、元胞位置k时，计算其换道概率。以向左换道为例，即

由于交通环境复杂性和驾驶员行为差异性等，对于满足前述换道动机和时机规则的车辆，不一定全部执行换道行为，而是以一定的概率进行换道。根据Gaussian 换道概率分布模型测算出的换道概率，构建3 步决策过程，伪代码如图7所示，最终确定是否换道。

图7 换道概率3步决策Fig.7 3-step decision on probability of lane-changing

3 数值模拟与分析

3.1 仿真设置

以图1中实例交织区构建元胞自动机模型，细化元胞尺寸及步长，将实测到达率、限速值等作为仿真程序的输入值。选取开口边界条件，当车辆车头位置位于仿真路段终点时，将车辆剔除车队。主要参数如表2所示。

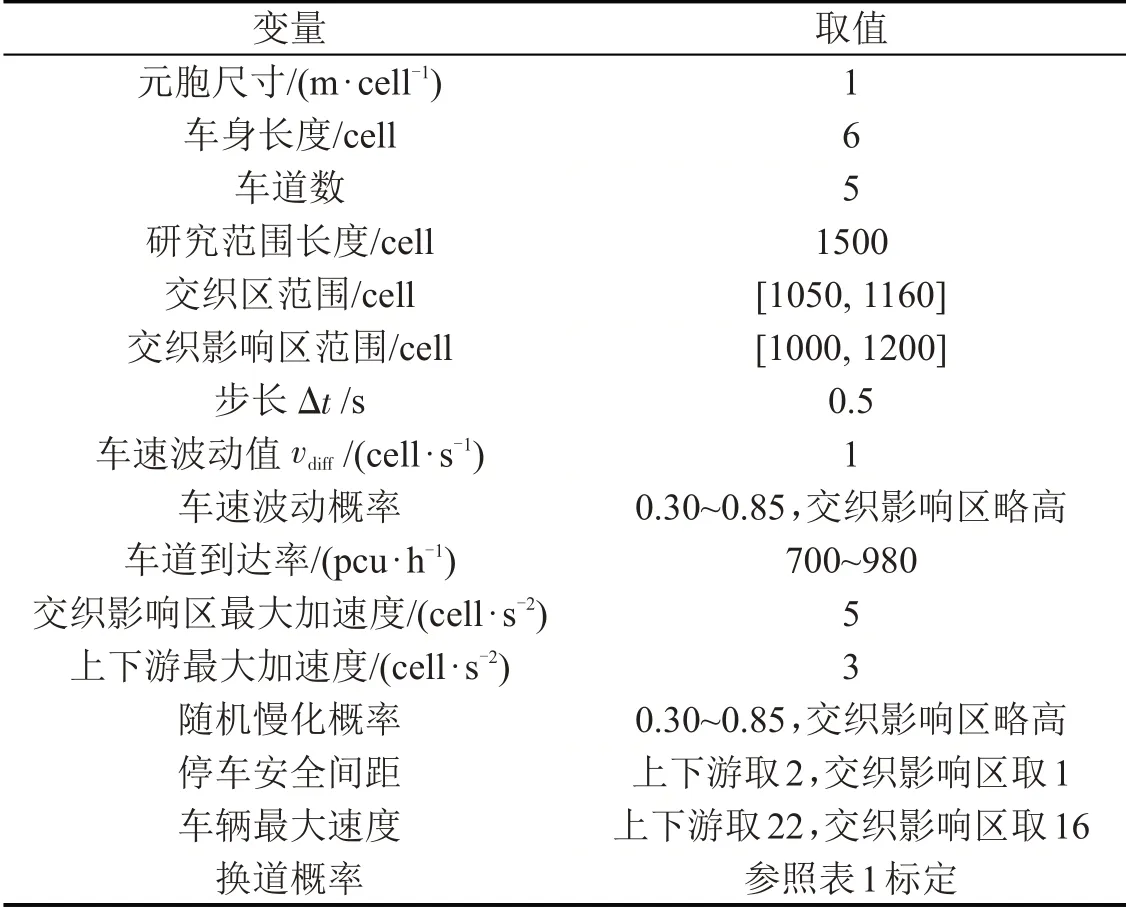
表2 模型参数Table 2 Model parameters

3.2 流量-密度-速度分布特性

为验证模型有效性，构建基于固定换道概率(取统计换道比例)的对比模型[1]。计算交织影响区实测平均流量、平均密度及平均速度，与本文Gaussian换道概率模型结果、固定换道概率模型结果进行对比。

表3给出各模型10000～13600时步的交织影响区车道平均流量、平均密度及平均速度，可以看出：

表3 模型结果对比Table 3 Model result comparison

(1)本文模型车道流量、密度和速度的误差均在0.7%～1.6%范围内，与固定换道概率模型相比，除了车道平均流量误差略高0.45%，密度和速度误差明显较低。

(2)与实测值相比，固定换道概率模型密度和流量明显偏高，而本文模型采用Gaussian分布换道概率模拟交织影响区车辆更为复杂的换道决策行为，特别是交织区范围换道概率明显高于邻近区域，可能降低车速形成交通瓶颈，流量、密度及速度与实际情况相符。

绘制流量、密度和速度分布图并进行多项式曲线拟合，方点为畅通及缓行阶段数据，圆点为拥挤及拥堵阶段数据，结果如图8所示。

(1)图8(a)流量-密度总体分布呈M状，在畅通或缓行阶段，车辆行驶基本不受交织干扰，随着密度增加、流量先增后降，流密关系与Greenshields模型一致。拥挤阶段：密度在[60,80]pcu·lane-1·km-1时部分车辆行驶受阻，此时为汇入主线、驶入匝道或寻求更大的行驶空间，车辆换道行为更为频繁，反而小幅提升了交通流量；随着密度继续增大，车辆间距明显变小、不易满足换道条件，此时交通处于拥堵状态，汇入、汇出主线强行换道会进一步恶化交通，流量显著降低。此外，拥堵阶段密度峰值约为90 pcu·lane-1·km-1、流量峰值约为900 pcu·h-1·lane-1时，与实测值基本一致。

(2)图8(b)密度-速度分布为线性函数关系，随着密度增加，速度减小，密度集中于[80,100]pcu·lane-1·km-1，速度集中于[7.5,17.5]km·h-1时，与实测值相符。

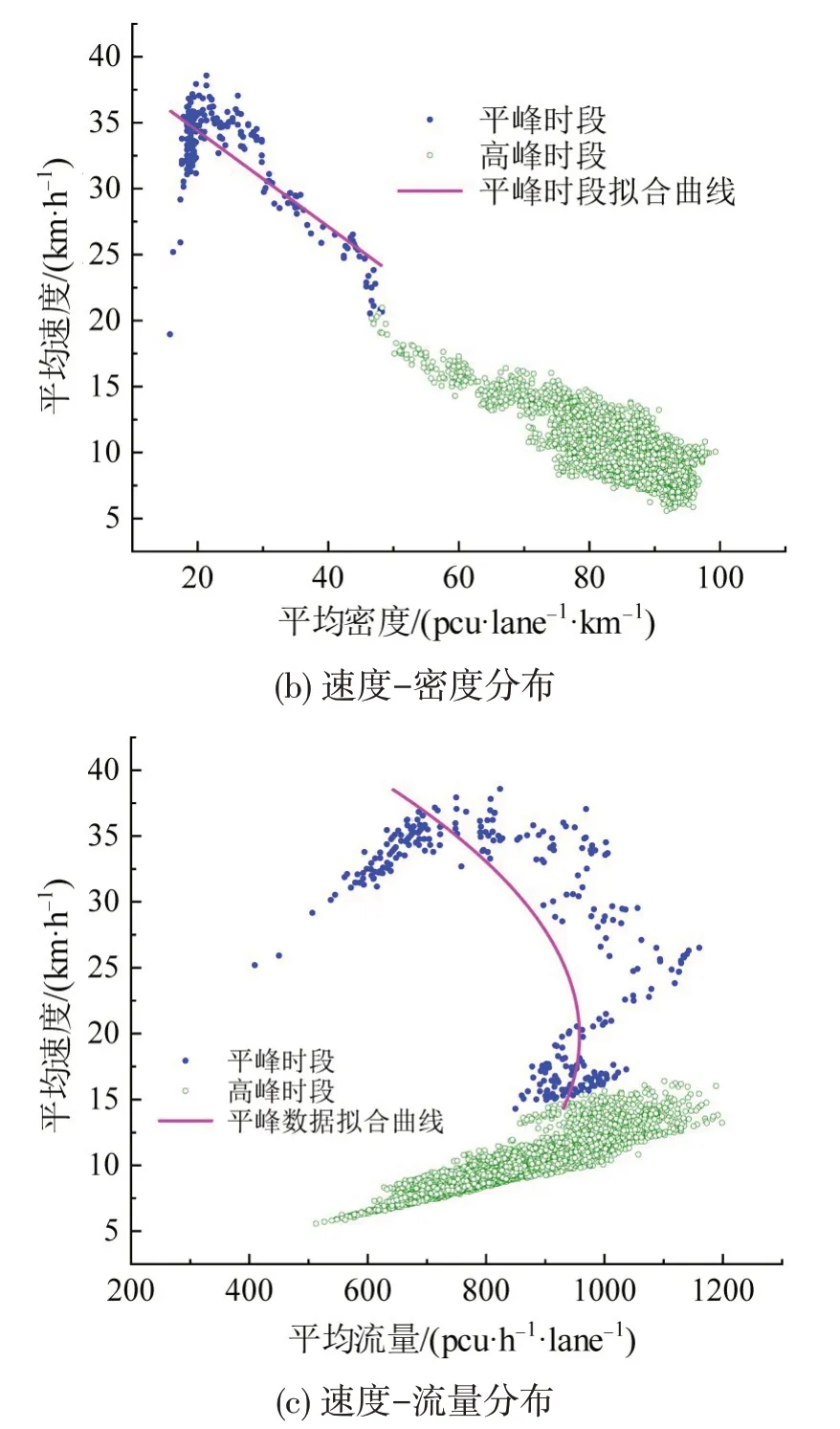
图8 交通流量、密度、速度分布Fig.8 Distributions of traffic volume,density and velocity

(3)图8(c)速度-流量曲线呈抛物线状，上半部分大体反映了交通状态由畅通到缓行的演化过程，随着流量增加，速度逐渐降低；曲线下半部分则反映了交通状态逐渐变为拥挤或拥堵，车辆速度较低、通行量也减少，较好地反映了交织区交通流特性。

总体而言，本文模型在畅通或缓行阶段交通参数分布规律符合Greenshields 关系，交通演变至拥挤和拥堵状态时，体现出区别于基本路段的交织区特性。

3.3 时空图分析

车辆时空轨迹可有效描述其换道分布情况，如图9所示，左侧虚线线段表示车辆在车道i跟车行驶至画圈位置处，满足换道条件，换道至车道i+1或i-1。同理，右侧画圈处则说明其他车道车辆换至车道i。

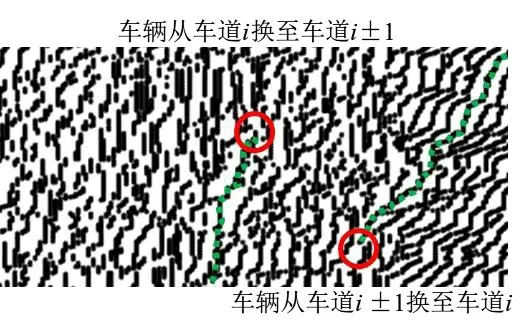
图9 时空图换道案例Fig.9 Time-space lane change case

以换道交织特征最显著的集散车道3为例，提取1～2000 时步时空轨迹点，绘制固定换道概率模型和本文模型的车辆时空轨迹图，如图10 和图11所示。

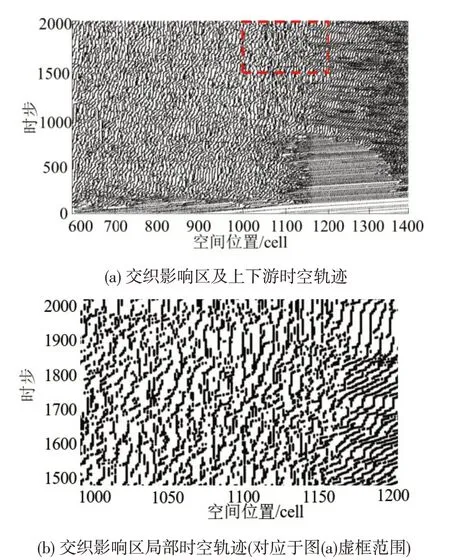
图10 固定换道概率模型车道3的时空轨迹Fig.10 Spatial-temporal trajectories of lane 3 resulted from lane changing model with fixed lane-changing probability

图11 本文模型车道3的时空轨迹Fig.11 Spatial-temporal trajectory of lane 3 resulted from proposed model

可以看出，固定换道概率模型和本文模型的时空轨迹全局图具有如下共性特征：上下游车辆轨迹比较连续、车流较为平稳，上游轨迹线斜率高于下游，即上游车速低于下游，而交织影响区车辆轨迹连续性较差、比较紊乱，说明这两个模型均能体现车辆频繁换道等行为形成的交织区瓶颈效应。

从时空轨迹局部图可以看出，固定换道概率模型交织区与其紧邻上游的轨迹比较一致，而本文模型交织区较其紧邻上游的车辆轨迹明显更紊乱，且越接近交织区中部紊乱程度越高，与换道行为集中在交织区、换道频率基本呈Gaussian分布的实际运行特性更相符。

3.4 换道分布特性分析

不同模型换道频率分布对比结果如图12所示，由图可知：

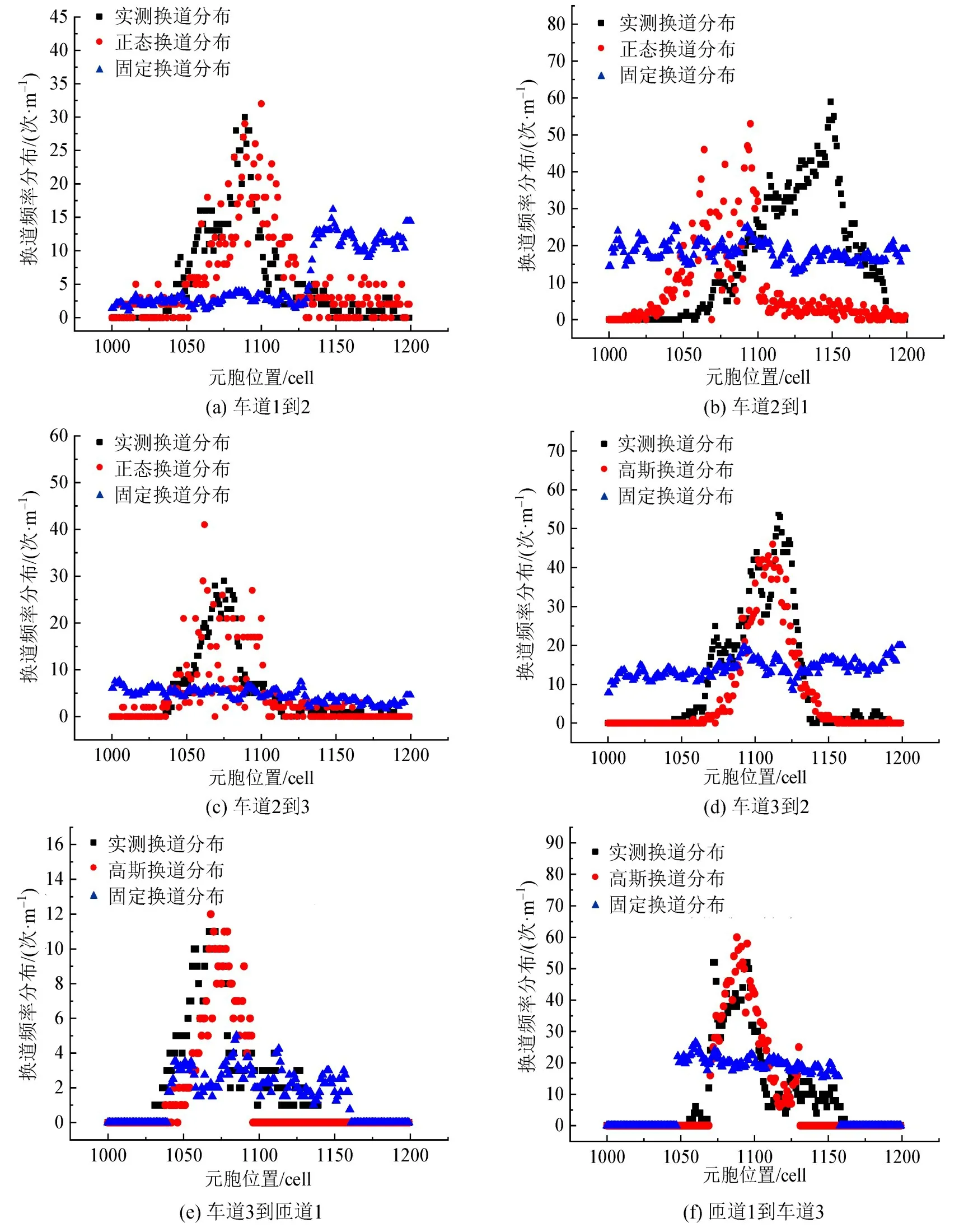
图12 不同模型换道频率分布对比Fig.12 Comparison of channel change frequency distribution of different models

(1)车辆实际换道行为多集中于交织区中部，在交织影响区前端或后端部分换道较少，本文模型仿真结果与该变化规律大体一致。

(2)对于本文模型，车道2换至车道1换道频率分布曲线与实测数据相比略向左偏移，但曲线形态、峰值与实测数据基本一致，而其余5个方向，换道频率分布跟实测数据吻合度较高。

(3)在交织影响区范围，固定换道概率模型的换道频率比较均匀，交织区与邻近区段换道频率几乎一样，无法体现真实的换道分布特征。因此，本文模型总体上体现了交织影响区真实的换道分布特性，明显优于固定换道概率模型效果，体现了本文模型的优越性。

4 结论

(1)上下游车辆换道的动机多是寻求更大的通行速度和行驶空间，其换道概率主要与跟车间距有关，与前车间距越小、换道概率越大，据此引入Logistic曲线模型可有效描述换道概率与跟车间距之间的关系。交织影响区车辆换道的动机较复杂，除了寻求更快的通行速度与更大的行驶空间外，还具有汇入汇出主线的路径转换需求，本文模型对上下游和交织影响区建立了不同的换道动机规则，可以反映车辆换道需求差异。

(2)交织影响区各车道换道频率与换道位置基本服从Gaussian 分布，且换道集中在交织区，本文提出换道概率Gaussian 分布模型并据此构建换道概率规则，能有效反映车辆在不同位置的换道强度。

(3)主线车道之间换道频率呈单峰Gaussian分布，而主线与匝道存在末端换道现象，换道频率呈双峰分布。