基于元胞自动机的高速公路瓶颈交通演化仿真

吕伟，黄广琛，汪京辉

(武汉理工大学，a.中国应急管理研究中心；b.安全科学与应急管理学院，武汉 430070)

0 引言

高速公路中的交通事故会造成临时性的道路收缩，形成交通瓶颈，很容易造成大范围的交通堵塞。因此，对多车道高速公路的临时道路瓶颈交通流开展研究对于缓解交通拥堵和优化交通事故处置具有重要的现实意义。

许多国内外学者着眼于交通瓶颈对交通的干扰现象进行研究，其中，元胞自动机作为一种微观离散的交通流仿真方法，是研究不同瓶颈路段下交通流变化规律的主要手段。杭佳宇等[1]对城市局部路段缩减场景进行建模，研究指出，2车道缩减为1车道的道路瓶颈中，汇流路段长度为100～120 m时，道路通行能力是最优的。李晓雪等[2]考虑到公交车进站停车造成的交通瓶颈，利用元胞自动机建模方法针对港湾式和非港湾式两种公交车停靠方式进行研究。于德新等[3]对于高速公路瓶颈区域的研究指出，可变限速控制方案能够缓解高速公路道路瓶颈区域的拥堵，其平均速度相较于固定限速控制提高了8.78%。姬浩等[4]对事故车辆影响下的城市3车道交通流开展元胞自动机仿真，考察了事故车辆停止位置和车道数量对交通流的影响。孙剑等[5]利用元胞传输模型对快速路入口匝道瓶颈的宏观交通流演化进行预测。焦朋朋等[6]的研究指出，车路协同环境下不同智能车辆渗透率的交通流通过瓶颈区的时间都有所减少。江欣国等[7]考虑交通瓶颈处的换道行为，研究指出，相较于安全换道行为，强制换道会显著降低道路的通行能力，提高交通事故风险。Hu 等[8]基于三相交通流理论对道路中临时停车行为造成的交通流状态变化进行研究。Fei 等[9]提出一种精细的双车道元胞自动机模型，对道路临时封闭造成的交通瓶颈进行建模。

本文在以上研究的基础上，利用改进的KKW模型和换道模型对道路瓶颈处的车辆跟驰和换道行为进行刻画，提高了仿真精度，以高速公路中一段3车道道路瓶颈场景为例，对道路瓶颈处车辆的微观交通特性进行研究。

1 仿真场景描述

仿真场景设置为在单向3 车道高速公路上，1辆车出现故障，停止在最右侧行车道上，司机及时下车并在车辆后方150 m 位置处放置反光三角警示牌，在反光三角警示牌位置前，临时出现一段由3车道收缩为2 车道的道路瓶颈。在车辆以高密度和高速度状态行驶的高速公路场景中，由于该道路瓶颈的出现，极易造成车辆拥堵，甚至造成交通事故。本文选取1.5 km路段建立模型，交通瓶颈出现在路段的1 km 位置处，抛锚车辆及三角架的具体位置如图1所示，假设驾驶员的视线范围为200 m，当车道3 上游车辆与三角警示牌间距小于200 m时，表示司机观测到三角架的存在，即存在一段200 m 的汇流路段，司机需要进行换道或者减速至停止对前方的障碍进行规避，本文通过建立车辆跟驰和换道模型，对此场景下的交通现象进行分析。

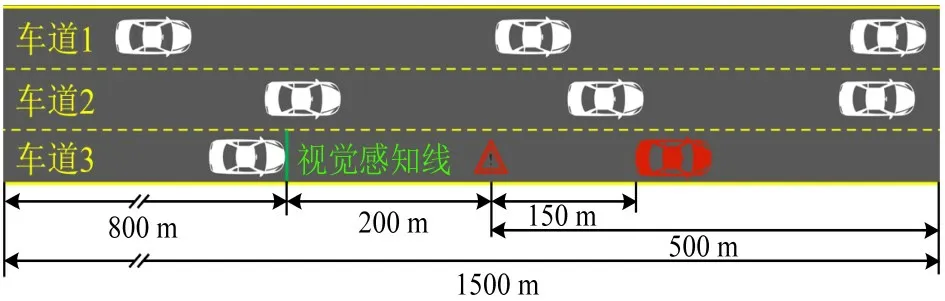
图1 道路临时交通瓶颈示意图Fig.1 Schematic diagram of temporary traffic bottlenecks

2 模型

2.1 跟驰模型

在元胞自动机交通流模型中，NaSch 模型[10]应用最为广泛，该模型简单，易于修改调整，但模型中大尺寸的元胞划分，无法很好模拟车辆的微观位置和速度变化。本文基于KKW 模型设置[11]，将单个元胞长度设置为0.5 m，并根据KKW模型规则进行修改，具体内容为：

(a)动态的加速度设置。不同于KKW 模型中的恒定加速度设置，在此模型中车辆的加速度依据其与前车速度差异在0～amax范围内波动，因而车辆在接近堵塞区及离开堵塞区过程的运动特点符合真实的车辆跟驰情况。

(b)动态的速度协同范围设置。KKW 模型中恒定的速度协同范围设置会导致高速车辆在接近堵塞区时，无法及时减速的现象，这同样与实际的车辆跟驰运动过程相悖，此模型中设置动态的速度协同范围，在同步流运动中车辆保持较小的速度协同范围，而在车辆接近堵塞区时，速度协同范围则相应较大。

车辆的速度更新过程分为动态项速度和随机项速度更新，动态项速度为车辆根据前车速度和车间距进行的确定性速度更新，随机项速度描述车辆的随机加速或减速过程，为非确定性速度更新，具体规则如下。

(1)动态项速度

①确定加速度a

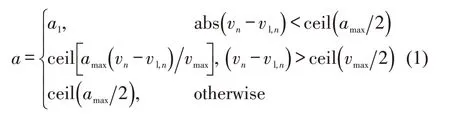
式中：ceil 为向上取整函数；vmax为最大速度；vn为当前车辆在第n时间步的速度；vl,n为当前车道上前方车辆在第n个时间步的速度；amax为最大加速度；abs为取绝对值函数。

②计算安全行驶速度vs,n

式中：gn为当前车辆与前车间距；τ为一个单位时间。

③计算协同速度vc,n

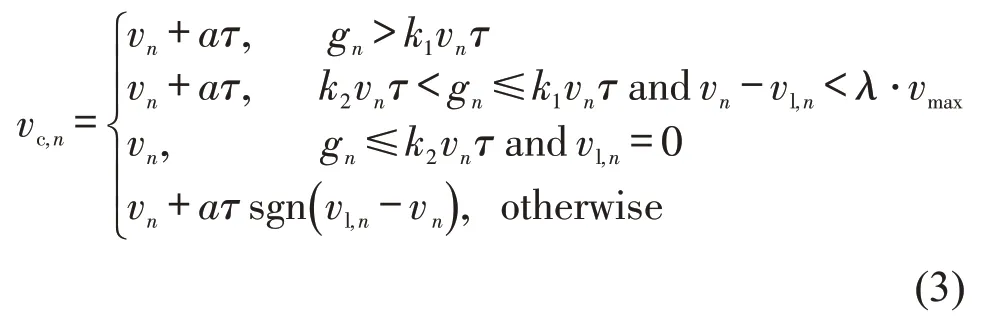
式中：k1,k2,λ为无量纲参数。

函数sgn(x)中，当x＞0 时，其值为1；当x=0时，其值为0；当x＜0 时，其值为-1。式(3)中的4项分别表示在不同车距和速度差条件下，表现出的不同运动特征。

④计算车辆在n+1时刻的动态项速度

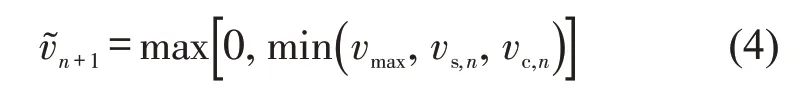
(2)随机项速度

①确定车辆加速概率pa(vn)

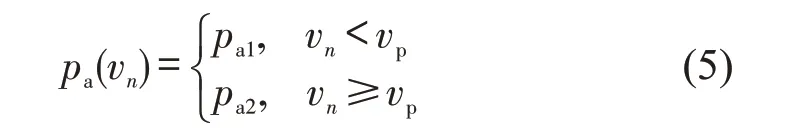
式中：vp为车辆加速概率变化的临界速度。

②确定车辆减速概率pb(vn)

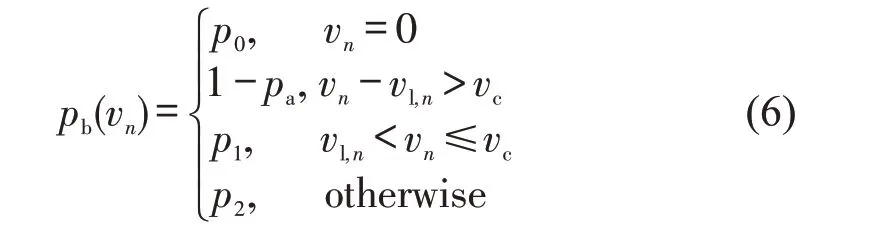
式中：vc为车辆减速概率变化的临界速度差。

③确定车辆在n+1时刻的速度vn+1

式中：ηn为速度扰动项。

④位置更新

其中，相关参数vmax,vc,vs,λ,τ,a1,amax,k1,k2,p0,p1,p2,pa1,pa2,vp的取值如表1所示。

表1 模型参数表Table 1 Model parameters setting

2.2 换道模型

在道路瓶颈场景中，车辆的换道意图可以区分为以最大速度行驶为期望的自由换道状态和以规避前方障碍物为期望的强制换道状态，在之前的研究中，考虑到车辆强制换道决策的心理和行为，提出了一个描述换道期望和执行概率的模型[12]，将此模型进行离散化表示，应用于本文道路瓶颈换道策略的研究，其换道过程可分解为产生换道动机，满足换道环境，换道概率计算和换道执行4个部分。

(1)换道动机

此场景中，车道3汇流路段内车辆为规避障碍物会采取强制换道策略，而其他车辆则均采取自由换道策略。在自由换道策略中，换道动机为获取更好的驾驶环境，即前方具备更广阔的行驶空间且具备速度优势。故车道a换道至车道b的换道动机为

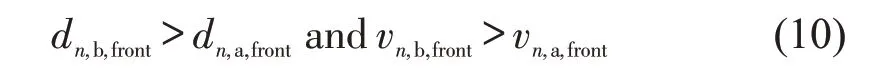
式中：dn,a,front为当前车辆与车道a 前方车辆间距；vn,b,front为车道b前方车辆速度。

(2)换道环境

车辆在进行换道时，需要考虑与目标车道后方车辆的速度与间距，以避免因间距过小发生碰撞，因此需要满足安全的换道环境。

车辆由车道a换道到车道b的安全条件为

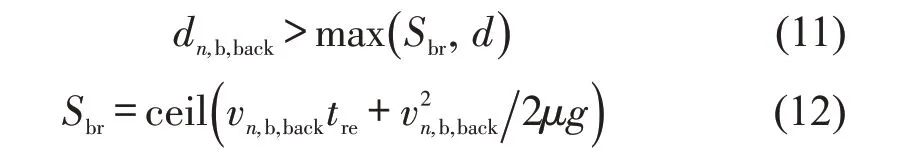
式中：d为车辆长度；dn,b,back为当前车辆与目标车道后方车辆之间间距；Sbr为目标车道上后方车辆的制动距离；vn,b,back为目标车道b 上后方车辆的速度；tre为驾驶员反应时间；μ为车辆与地面的摩擦系数；g为重力加速度。

(3)换道概率

当满足上述两项条件后，表示车辆可以进行换道，但是对应不同道路环境和换道行为，驾驶员会产生不同的换道期望，强制换道条件下的换道概率为100%，即当满足安全换道环境则一定换道，而在自由换道条件下，车辆由车道a 换道到车道b 的换道概率为

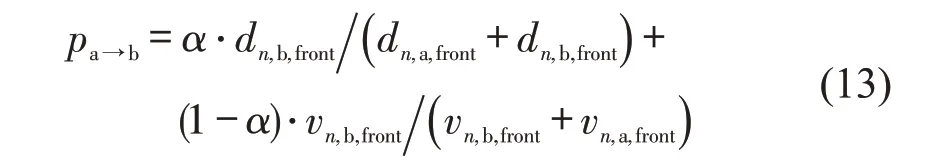
(4)换道执行

当车辆位于车道1 或车道3，或者车辆位于车道2，但只有一条车道满足换道要求时，换道执行条件为

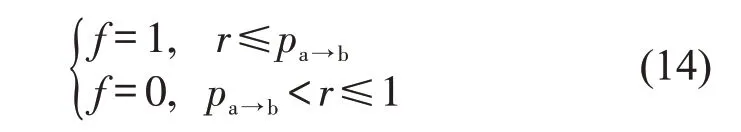
式中：f=1 为进行换道，f=0 为不进行换道；r为随机数。

当车辆位于车道2 时，如果车道1 和车道3 都满足换道的要求，其执行条件为

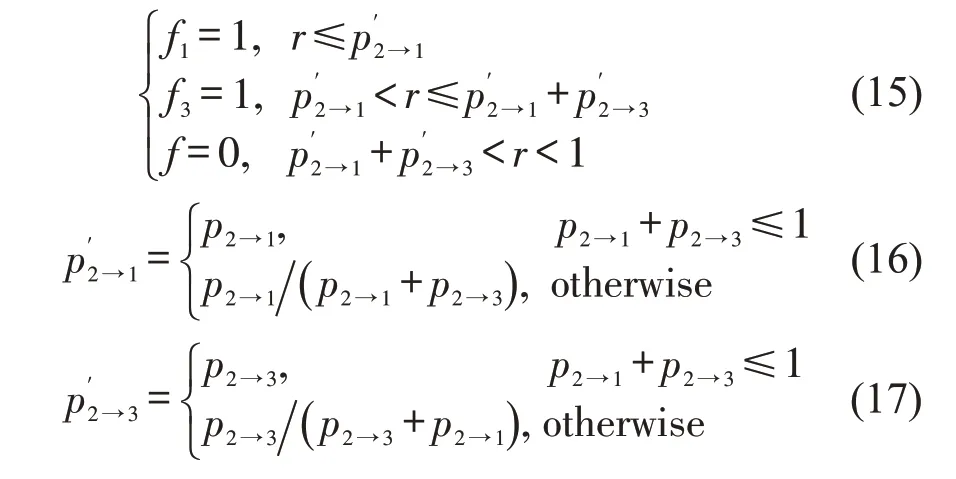
式中：f1=1为车辆换道到车道1；f3=1为车辆换道到车道3；p2→3为车辆从车道2 换道到车道3 的计算概率；为车辆从车道2换道到车道3的标准化概率；和同理。模型参数取值如表2所示。

表2 模型参数表Table 2 Model parameters setting

3 数值模拟与分析

仿真边界条件设置为开放性边界条件，元胞长度为0.5 m，车辆类型仅考虑小型车辆，长度设置为6 m，对应12个元胞长度，道路长度设置为1500 m，对应3000 个元胞长度，相关参数的设置如表1和表2所示，最大速度设置为108 km·h-1，即60 cell·(time step)-1，每个时间步对应真实时间1 s。为具体分析该道路瓶颈场景的各交通参数和特征，本文设置4 种仿真场景，如表3所示。各场景初始仿真环境相同，如图1所示，道路瓶颈设置在道路的1 km 位置处，初始仿真环境中无车辆。在仿真初期，存在进车过程，交通流状态并不稳定，故在表3给出的仿真时间之前需要进行预仿真处理，预仿真时间为1000 s，预仿真时间不纳入仿真时间统计，与各场景最终仿真结果无关。

表3 仿真场景设置Table 3 Setting of simulation conditions

3.1 时空图分析

为对瓶颈产生和移除后的交通流特征进行综合分析，本文在表3 场景1 的仿真设置中增加了交通瓶颈的移除过程。图2为场景1仿真环境下3条车道上的时空图分布情况，从图中可以看出：当进车流量很低时(400 veh·h-1·lane-1)，车辆与车辆之间保持较远的行车间距，车道3上的大部分车辆能够及时换道到车道2，道路瓶颈对交通的影响较小；当进车交通流量上升至800 veh·h-1·lane-1时，车辆之间的行车间距收缩，车道3上的车辆没有足够的换道空间，少量车辆减速到静止在瓶颈前聚集，当足够的换道空间出现时，低速的车辆会集中地进入车道2，车道2 上的后方来车由于速度的同步效应会进行减速，在上游区域形成小区域的低速同步流状态；随着进车交通流量进一步上升(1200,1600,2000 veh·h-1·lane-1)，车道3 中出现较长的堵塞区域，并且由于集中密集的换道行为，车道2 上会出现堵塞现象，车道1上会出现大范围的同步流运动特征。

为分析饱和流量下换道行为的微观特征，对进车交通流量为2000 veh·h-1·lane-1环境下车道2 和车道3 的速度时空分布图进行局部放大，如图3所示。从车道3 中可以观察到，随着时间的增加，瓶颈前首先出现排队长度上升，而后，当车道2 中出现换道空间，一低速车辆换道至车道2，由于换道车辆与目标车道上前车速度差异较大，换道车辆会经历一段加速运动过程，这会进一步导致车间距的增加，为其他车辆的换道行为提供条件，从而导致集中的换道现象。对应于图3 左侧可以发现，在车道2中，高速运动车辆与换道车辆在时空图中出现明显的分割现象，表明低速运动波随着时间的推进向交通下游蔓延，这种现象同样可以在图2左侧车道1的时空图中观察到，如果将这种由单个车辆换道引发的雪崩式换道行为视为一次“集群换道”过程，可以发现，随着进口交通流量的上升，“集群换道”频率相应下降，而换道过程造成的影响范围(时空尺度)相应扩张的规律。

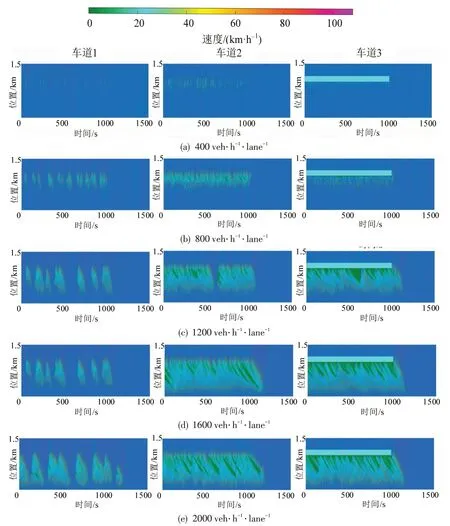
图2 3条车道上不同交通量下的时空图Fig.2 Time-space diagram of different traffic volumes on three lanes

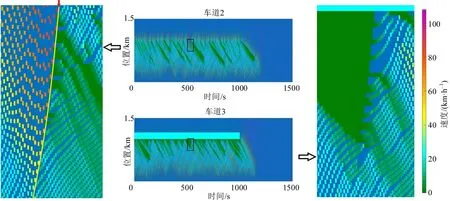
图3 车道2和车道3上局部放大时空图(交通量为2000 veh·h-1·lane-1)Fig.3 Partially enlarged time-space diagram on lane 2 and lane 3(traffic volume is 2000 veh·h-1·lane-1)

图2中，在稳定的输入流量条件下，车道3中道路瓶颈前的拥堵区域没有随时间的增加而增长，而是处于一种动态平衡状态。这是因为一方面上游源源不断的来车会造成排队长度的上升，另一方面密集的换道行为会在短时间内缩短排队长度。为进一步分析此现象进行，对场景2 开展了6000 s 的仿真。场景2中各进口流量条件下车道3的时空图如图4所示。从图中可以看出，在进车流量为1200、1600 和2000 veh·h-1·lane-1时，道路瓶颈前都出现了稳定的拥堵区域，这种状态的先决条件是道路的出口交通量近似等于其入口交通量。在低速区域中，排队长度会随着时间的增加在恒定的范围内波动，并且，随着进车交通流量的上升，拥堵区域的范围也会随之增加。

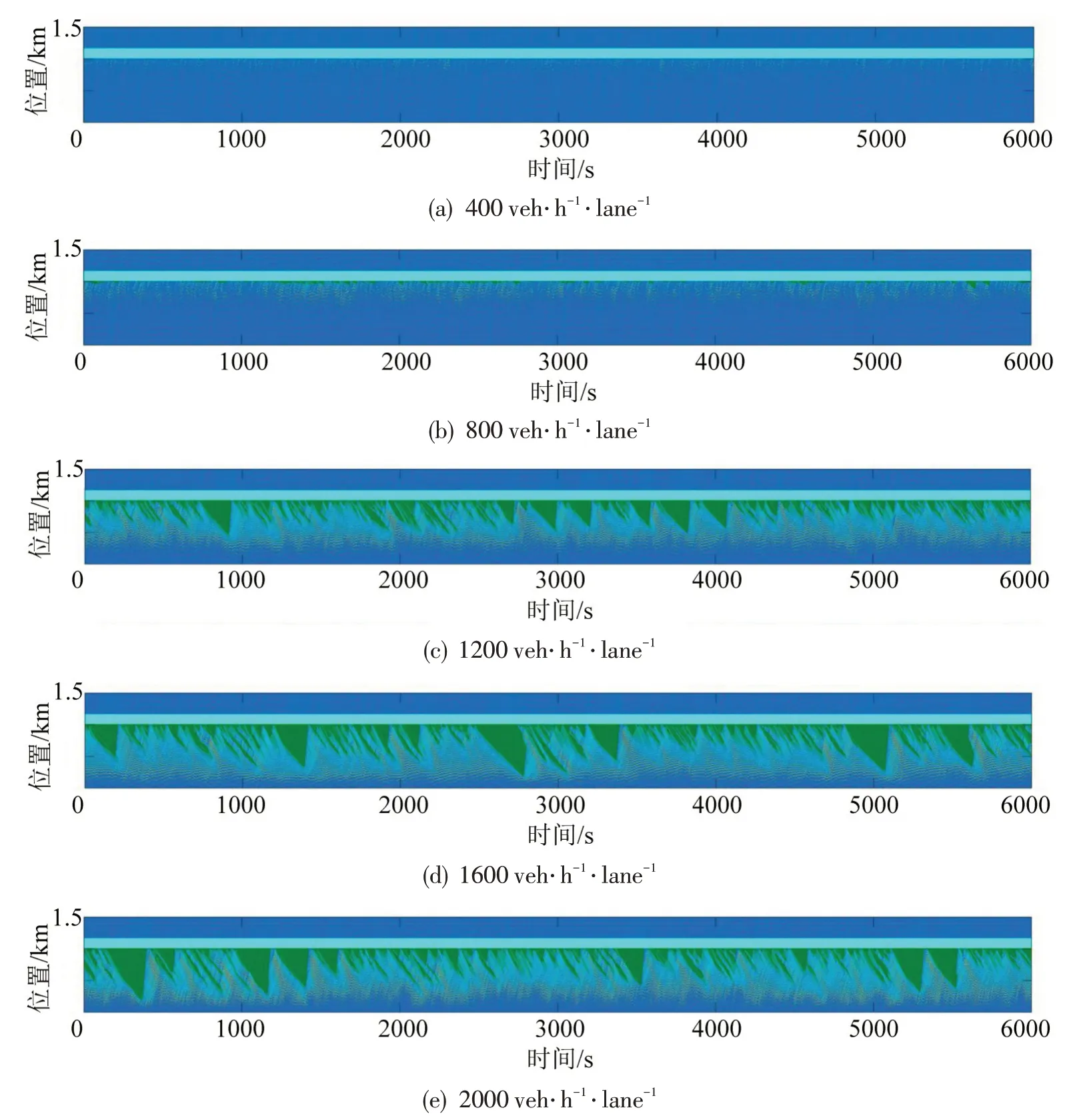
图4 不同流量条件下车道3上的时空图分布Fig.4 Distribution of time-space diagram on lane 3 under different traffic volume

3.2 交通参数演化分析

图5 和图6 为场景1 仿真中3 条车道在不同进车流量条件下每条车道上车辆数和平均车速的变化情况。从图5中可以看出：当道路的进车交通量较低时，车道3 上的车辆数量低于车道1 和车道2，而车道1 和车道2 上的车辆数差异较小；当进车交通量高于1200 veh·h-1·lane-1时，车道2 和车道3 上车辆数较为接近，且明显高于车道1。从数据的波动特征来看，随着进口交通量的上升，“集群换道”现象开始出现，而集群规模随进口交通量的上升而上升。在交通瓶颈被移除后，3 条车道上的车辆数会在短时间内趋于一致，恢复动态平衡的状态。

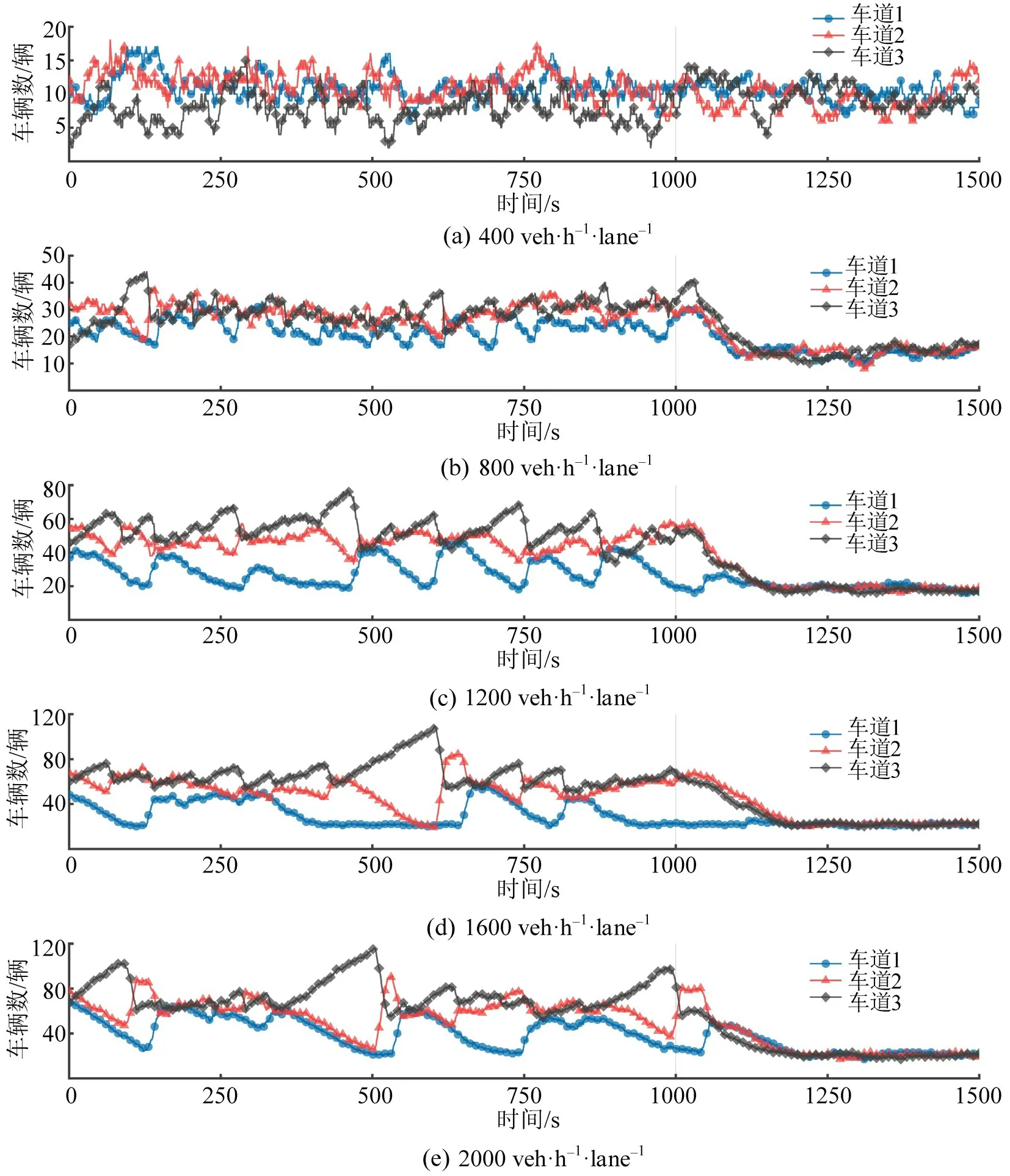
图5 不同进车流量下3条车道车辆数变化Fig.5 Changes in number of vehicles on three lanes under different traffic flows

从图6 中可以看出随着交通量的上升3 条车道上的速度变化情况。当进车交通流量为400 veh·h-1·lane-1时，车道1上速度波动较小，与之相对应的，车道2 上的速度波动较为明显，表明在较低交通量条件下，远离道路瓶颈的车道受到的影响较小。随着交通量的上升，由于密集的换道行为，车道1上的交通呈现出剧烈的震荡，而车道2和车道3 上的速度在不同交通量条件下始终比较接近，表明在3 车道交通瓶颈系统中，车辆汇流对目标车道影响较大，对远离汇流区的车道影响较小。在图6的第1001 s时刻，交通瓶颈被移除，从速度变化中可以观察到道路交通在瓶颈移除后的恢复情况，图中随着进口交通量的上升，交通恢复时间存在明显的增长趋势。

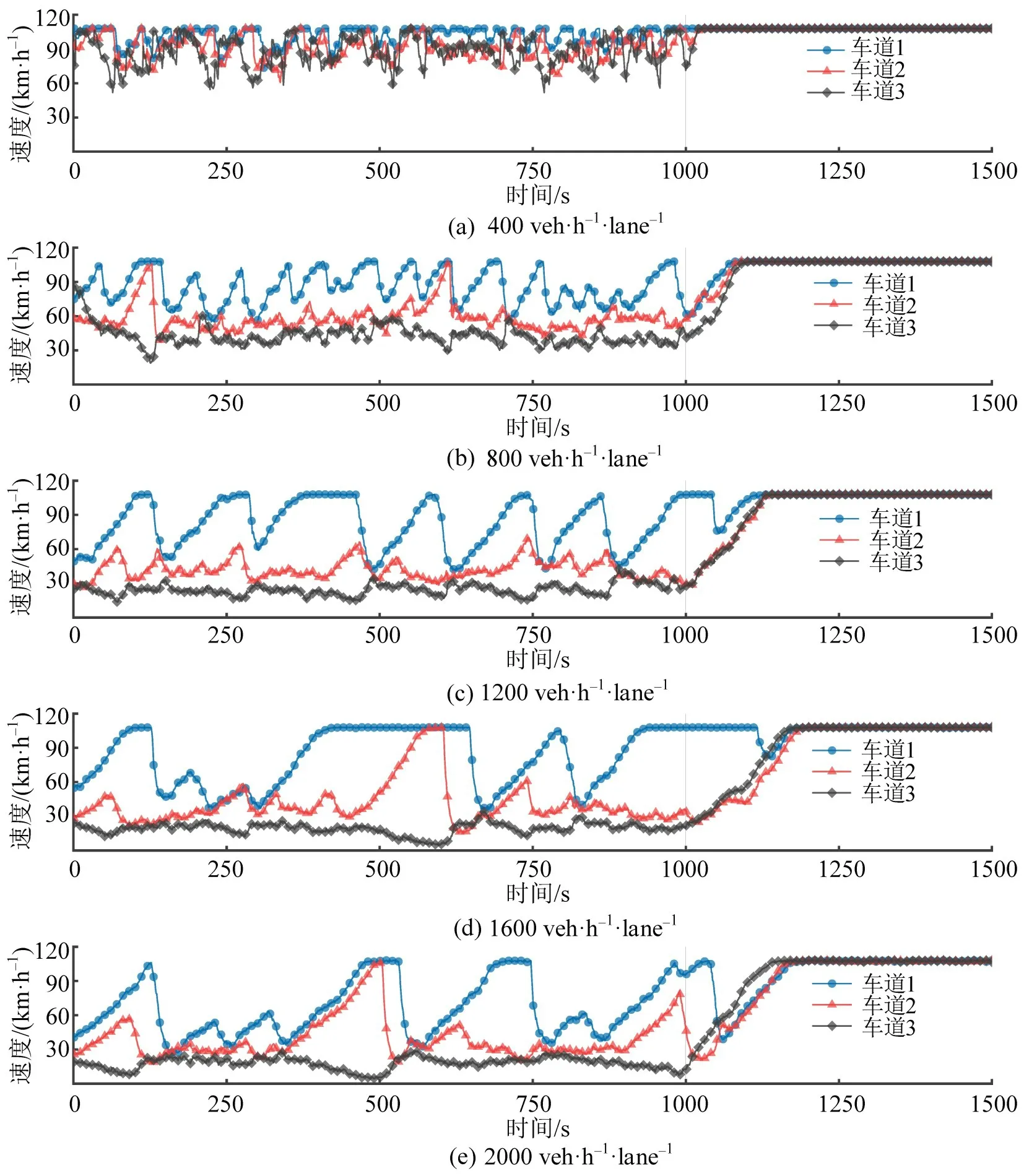
图6 不同进车流量下3条车道速度变化Fig.6 Changes in speed of vehicles on three lanes under different traffic flows

为进一步分析交通恢复时间随进口交通量的变化关系，本文设置了场景3对各进口交通量条件下交通恢复时间进行统计，每组分别进行10 次独立仿真并取平均值，绘制出进口交通量和交通恢复时间的对应关系如图7所示，拟合结果表明，瓶颈处交通恢复时间随着进口交通量上升呈现线性增长的关系。

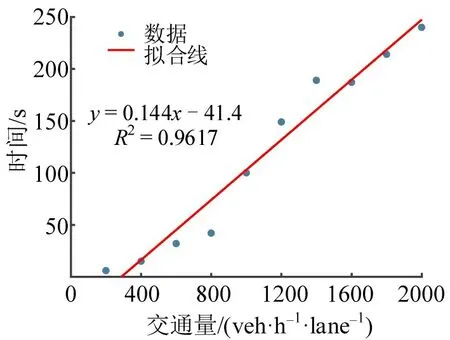
图7 交通恢复时间和交通量对应关系Fig.7 Correspondence between traffic recovery time and traffic volume

3.3 车道间速度和流量差异

为分析不同流量下道路瓶颈造成的车道间交通参数差异，根据场景4 设置，每组分别进行10 次独立仿真，提取每次仿真的速度和流量均值进行统计，得出不同交通量条件下3 条车道上的速度和流量变化如图8所示。在速度图中可以发现，以1000 veh·h-1·lane-1为临界进车流量，3条车道中流量上升趋势和速度下降趋势在经过该临界点时开始减缓，车道2 与车道3 的平均速度下降趋势一致，而车道1受到道路瓶颈的影响较小。在流量图中：车道1和车道2上流量的上升趋势一致，呈现随交通量上升而上升的趋势；从数据的波动情况看来，随着交通量的上升，道路瓶颈引起的交通震荡现象更加明显，3 条车道中车道2 上的速度和流量波动最大。

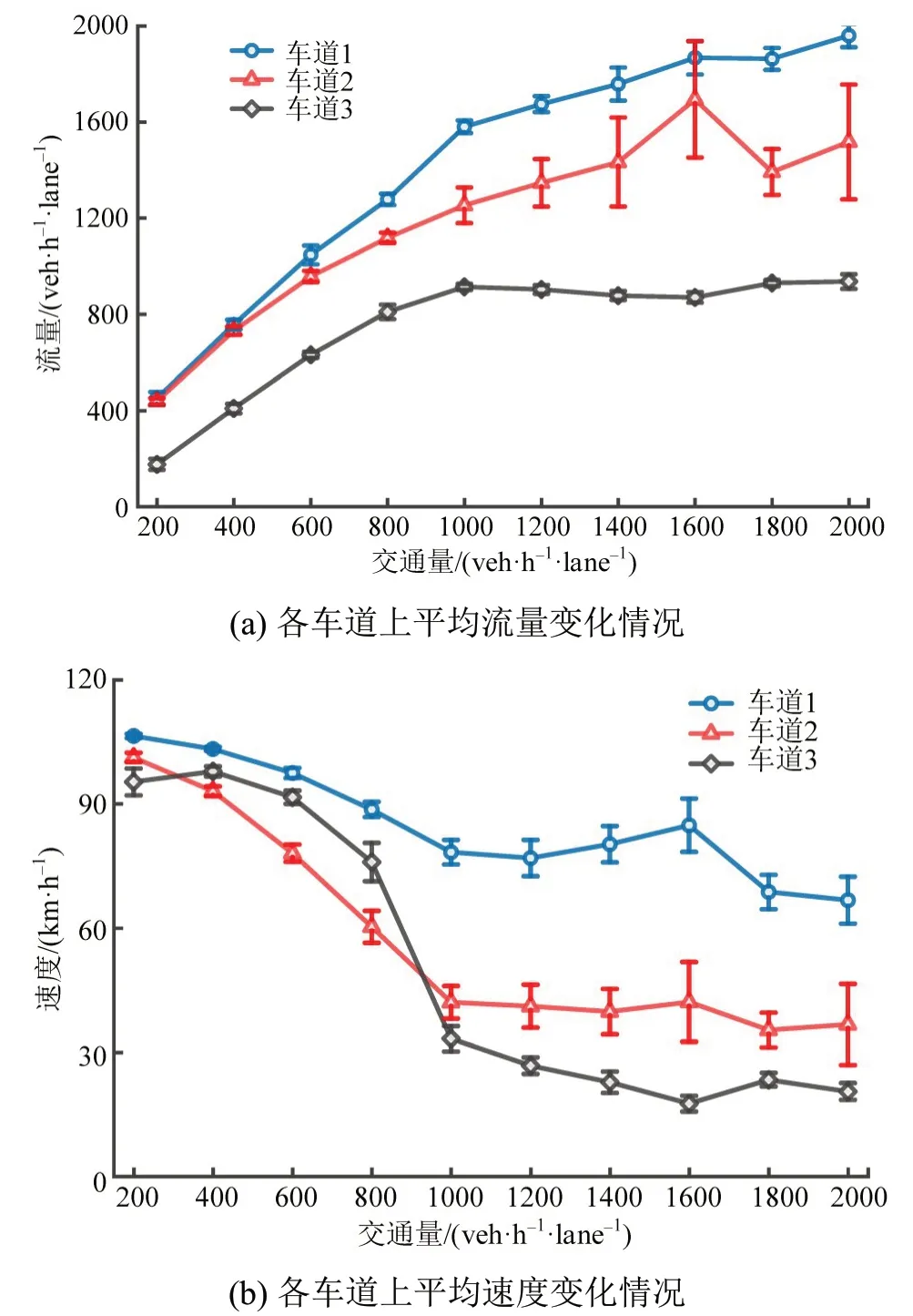
图8 3条车道上车辆速度和流量随交通量的变化关系(均值±标准差)Fig.8 Relationship between speed and flow rate with traffic volume on three lanes(mean±SD)

4 结论

本文通过改进KKW 模型，考虑自由和强制换道规则，应用于3 车道道路瓶颈系统展开建模研究，得到的主要结论如下：

(1)针对换道行为的分析指出，较长范围拥堵的低速车辆倾向以小集团进行统一换道，这种“集群换道”行为会在目标车道的时空图中呈现速度分割现象，造成更为剧烈的交通震荡。

(2)在本文给定的交通流量状态下，汇流路段的排队长度并不会伴随着时间的上升而增加，而是在道路瓶颈前出现较为固定的拥堵区域，在此区域内，排队长度随时间在恒定范围内动态变化，在瓶颈消失后，交通恢复时间随着交通流量的上升呈现线性增长的趋势。

(3)3 车道道路瓶颈系统中，随着交通量上升，车道1 和车道2 的流量变化趋势一致，而车道2 和车道3的速度变化趋同，以1000 veh·h-1·lane-1为进车交通量临界值，交通参数的变化趋于稳定。

本文的研究可应用于高速公路道路瓶颈造成的拥堵区域范围及交通恢复时间的预测。