自适应期望跟车间距和行为习惯的驾驶人跟驰模型

倪捷，张凯铎，刘志强，葛慧敏

(江苏大学，汽车与交通工程学院，江苏镇江 212013)

0 引言

道路交通事故统计数据表明[1]，由驾驶人因素引发的交通事故在事故总量中占有非常大的比重。为尽可能地降低驾驶人因素导致的交通事故的发生，减轻驾驶人的操作强度，相继采用了各种先进的驾驶辅助系统。然而，由于驾驶人个体属性、心理特征、驾驶经验及对道路环境感知的不同，在跟车、换道及制动等方面表现出典型的差异性。目前，智能车辆采用的驾驶人模型主要为传统的基于逻辑和经典控制方法，难以适应不同驾驶人的驾驶习性，人-机交互协同的满意度和接受度都有待提高。因此，为满足智能汽车的个性化用户需求，采用的驾驶人模型应能针对驾驶人个体或群体进行自适应调控，以适应驾驶人的行为特性差异。

跟驰模型一直是交通流理论的研究热点，随着辅助驾驶和自动驾驶汽车的发展，跟驰模型作为驾驶人模型之一开始广泛应用于智能汽车领域。目前，跟驰模型分为两类：基于物理建模的跟驰模型和基于数据驱动的跟驰模型。基于物理的模型，将驾驶人的跟驰行为以固定的数学形式进行表达，并利用实验数据标定数学模型参数。GIPPS等[2]假设驾驶人的驾驶行为特性会收敛到一定的车距和自由车速，称为期望车距和期望车速，据此设计安全距离跟驰模型；杨龙海等[3]考虑实际车头间距和平均速度的关系，构建改进的优化速度函数跟驰模型；BOLDUC 等[4]提出一种多模型方法，在多个跟驰模型中查找适用于单个驾驶人的最优模型，以更好地模拟个体驾驶人的纵向跟驰行为。

基于数据驱动的跟驰模型以车辆轨迹数据为建模基础，通过数据驱动方法对车辆轨迹数据进行统计分析，挖掘数据中关于驾驶行为的内在规律，并建立对应数据的拟合关系，预测驾驶行为。同时，随着智能汽车的快速发展，可以获取更大规模和更高精度的车辆轨迹数据，基于数据驱动的自学习模型成为主流方法。ZHANG 等[5]将道路信息引入驾驶决策，采用不同核函数的支持向量回归模型建立适用于自动驾驶车辆的驾驶决策模型；ZOU等[6]采用逆强化学习，通过学习历史数据建立相应成本函数，进行个性化驾驶行为建模；WANG 等[7]分析多种车载传感器参数，根据加速踏板操作将驾驶人跟驰行为分为多种决策状态，并利用支持向量机建立驾驶人行为预测模型。HUANG等[8]基于长短期记忆神经网络建立跟驰模型，研究与非对称驾驶行为密切相关的时滞现象和驾驶人的不完美驾驶行为等。

上述两类模型各有优劣，基于物理建模方法的跟驰模型在一定程度上模拟了驾驶人的驾驶行为特性，具有逻辑性强和解释性强的优点，但结构化数学模型考虑的影响因素较少，在描述驾驶行为时误差较大，难以模拟驾驶过程的非线性和不确定性；基于数据驱动的模型能够模拟出不同驾驶风格特性，通过对输入特征参数的拟合来预测不同驾驶人的跟驰行为，但容易忽略内部特征参数之间的状态关系，关键特征有待进一步发掘，同时，需要驾驶人特性相关的先验理论，易出现过拟合问题。基于此，本文考虑驾驶人的跟驰行为受不同环境下期望跟车间距的直接影响，从而表现出特定的跟车行为习惯，提出一种个性化的双层驾驶人跟驰模型。第1 层模型，基于高斯混合和概率密度函数建立驾驶人期望跟车距离模型；第2 层模型，引入期望跟车距离参数，基于高斯混合-隐马尔可夫模型建立学习模型，预测跟驰过程中的加速度序列；最后，采用自然驾驶行为数据验证模型。

1 跟驰行为特性及描述

车辆跟驰行为是最基本的微观驾驶行为，描述了在限制超车的单车道上行驶车队中相邻两车之间的相互作用。文献[2,4]表明：车辆在非自由运动状态的车队中具有制约性、延迟性及传递性的行驶特性；同时，驾驶人在跟驰过程中会试图维持一个期望的跟车距离，并与前车维持稳定的相对速度。但由于受车辆的行驶环境、两车的行驶状态(车间距，车速等)以及驾驶人驾驶风格特性的影响，不同的驾驶人在跟驰行为上表现出明显的差异性。本文主要研究驾驶人在城市快速路工况下跟驰行为，考虑驾驶人期望跟车间距和行为习惯对跟驰行为的影响，建立符合驾驶人特性的个性化驾驶人跟驰模型。

跟驰过程按照主车与前车的距离和速度变化，分为均衡状态和非均衡状态。在车间距较远且未满足期望车速情况下，主车会加速保持所期望的跟车间距；在车间距较近或者前车急减速的情况下，主车会减速保持所期望的跟车间距，这两个过程为跟驰的非均衡状态。当达到期望跟车距离后，车辆保持相对稳定速度行驶，进入跟驰的均衡状态。将跟驰行为特征表示为由速度传感器获得，为第t时刻两车的车辆状态参数，分别表示主车(Host Vehicle)的速度和加速度，前车(Leading Vehicle)的速度和加速度；Δdt、Δvt由毫米波雷达和视频影像传感器获得，分别表示第t时刻两车跟车间距和相对车速；和通过对以上参数进行二次计算得出，分别表示第t时刻跟车时距和碰撞时间倒数。

2 双层驾驶人跟驰模型

2.1 模型结构

考虑驾驶人跟车工况中的均衡状态和非均衡状态，建立符合驾驶人驾驶习性的双层跟驰模型，设计框架结构。首先，标定均衡跟驰状态下的数据，建立基于驾驶人个体特征的期望跟车距离预测模型，即为第1层模型；然后，将模型生成当前时刻的期望跟车距离，与当前时刻的自车和周围车辆信息构建个性化跟驰行为特征集；最后，基于数据驱动，采用参数化方法，建立驾驶人跟驰行为模型，即为第2层模型；模型生成符合驾驶人驾驶习性的车辆运动参数序列，在本文中为加速度序列，框架结构如图1所示。

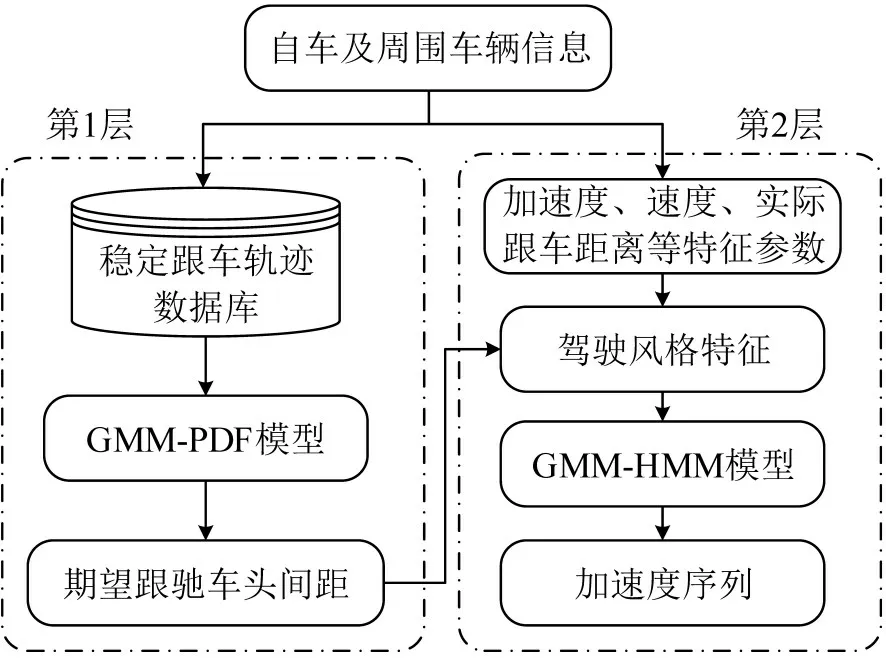
图1 模型框架Fig.1 Framework of mo del

其中，第1层模型通过高斯混合模型拟合均衡跟驰状态下的轨迹数据，建立期望跟车距离与其他轨迹参数的联合密度函数；第2层模型通过个性化特征参数训练高斯混合-隐马尔可夫模型，实现跟驰模型的个性化设计。文献[9]表明，加速度、与前车相对距离、相对速度、跟车时距及碰撞时间倒数可以有效表现驾驶人的个性化跟车行为。训练参数与预测参数之间的相关性应尽可能的低，第1层模型预测期望跟车间距ΔDt，输入参数为。第2 层GMM-HMM模型的参数选择综合跟驰行为特征参数和期望跟车距离，定义为，其中，。双层混合模型的关系及各层模型的输入和输出参数如图2所示。

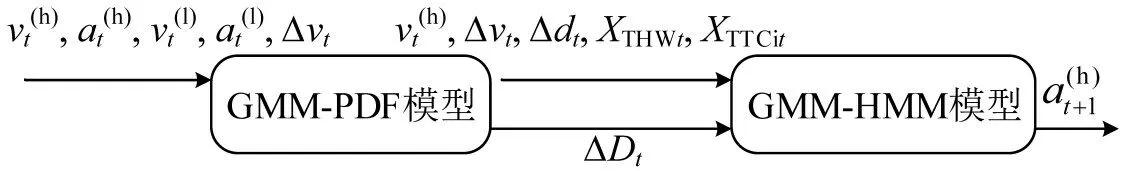
图2 模型参数Fig.2 Parameters of model

2.2 第1层模型

第1 层模型即期望跟车间距预测模型(GMMPDF 模型)，采用高斯混合模型拟合不同驾驶人的跟车轨迹数据，建立自适应驾驶人的概率密度函数，并以跟车间距为自变量，使概率密度函数最大的值作为驾驶人的期望跟车间距。

GMM模型参数输入为xt={}ξt,Δdt，使用K个高斯模型拟合数据，假设每个高斯模型分量中的数据服从高斯分布，即

式中：μk为第k个高斯模型的均值；Σk为第k个高斯模型的协方差矩阵。该高斯分布的分布密度函数为

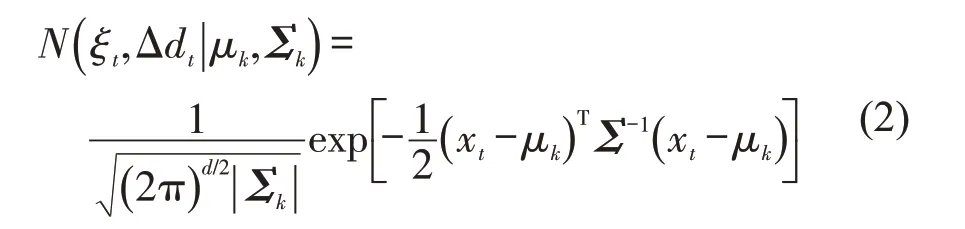
式中：d为数据维度。则所有数据的联合概率密度函数用高斯混合模型表示为

式中：K为高斯模型分量的个数；πk为第k个高斯模型的权重，。

采用均衡跟驰数据训练不同驾驶人的GMM模型，模型参数θ通过期望最大化(EM)算法估计，对数据进行K-means 聚类，将其结果作为EM 算法迭代的初始值。

期望跟车距离的估计可以基于PDF算法，即令GMM的概率密度函数最大化。

2.3 第2层模型

第2层模型即加速度预测模型(GMM-HMM模型)，高斯混合-隐马尔科夫模型是关于时序的概率模型，可以将前后时刻的状态联系起来。驾驶行为具有强烈的时序性，一个连续的驾驶行为由驾驶人在相应时刻的操作构成，体现为一系列观测参量。驾驶人根据当前时刻的车辆状态、周围环境信息以及驾驶习性，决定下一时刻的行为(加速、减速或定速行驶)。

本文将高斯混合模型中的高斯模型分量作为隐马尔可夫模型的隐含状态Q={N1,N2,…,Nk}，模拟驾驶人的驾驶习性，将车辆轨迹参数作为观测向量。HMM结合上一时刻和当前时刻的隐含状态生成当前时刻的观测向量。

HMM 表示为λ={Π,Ψ,ϒ}，其中，Π为初始状态概率分布，即高斯混合模型中的πk，，s为当前状态；Ψ为状态转移矩阵，表示从隐含状态Ni转移到状态Nj的概率，；ϒ为隐含状态j条件下生成观测数据xt的概率，，其中，表示为

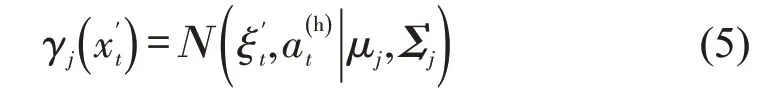
式中：μj、Σj分别为第j个单高斯模型的均值、协方差矩阵。

基于历史数据，使用Baum-Welch 算法估计不同风格驾驶人的HMM模型参数，通过计算下一时刻使概率密度函数值最大的参数预测车辆加速度。

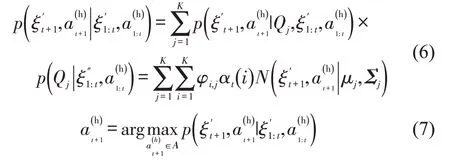
式中：αt(i)为t时刻的前向概率；A为主车加速度可能的取值。

2.4 模型评价方案

为评价本文所提出的自适应期望跟车间距和行为习惯的双层跟驰模型的预测效果，将其与经典Gipps模型[2]、ODM模型[10]、单层模型及通用模型展开对比分析，验证模型的适用性和有效性，各模型结构如下。

(1)Gipps 模型是经典的基于安全行驶跟车距离的车辆跟驰模型，表达式为

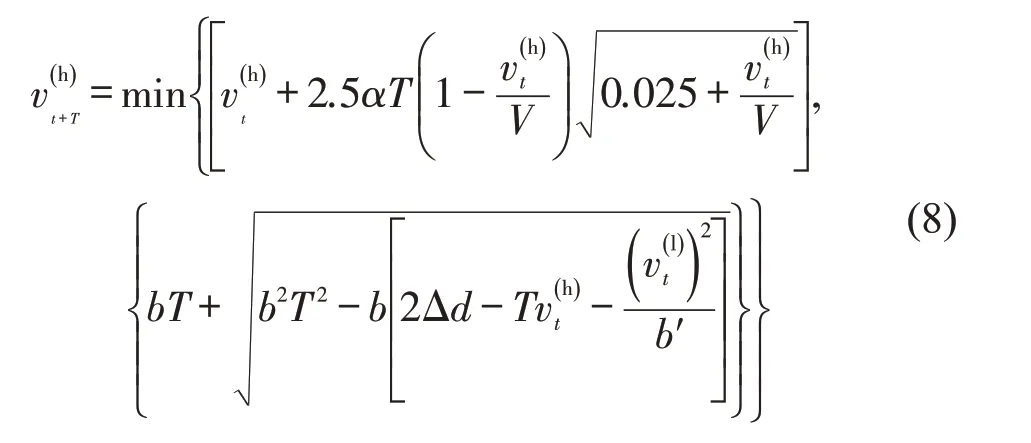
式中：α、V、b、b′为待标定的参数；T为反应时间。

(2)ODM 是以经典的刺激-反应原理为基础，假设在跟驰状态下，驾驶人倾向保持最优跟车距离行驶，表达式为

式中：τ、X1、X2、β、θ′为待标定参数。

(3)单层模型是以GMM-HMM模型为基础，考虑驾驶人个体差异性，使用个体数据进行训练，其中，模型输入为。

(4)通用模型是以本文模型为基础，未考虑驾驶人个体差异性，即将所有驾驶人数据作为训练集所得到的一般驾驶人跟驰模型。

在模型性能分析中，引入平均绝对值误差eMAD作为模型预测结果衡量的标准。eMAD可以衡量预测值与实际值at之间的偏差，表示为

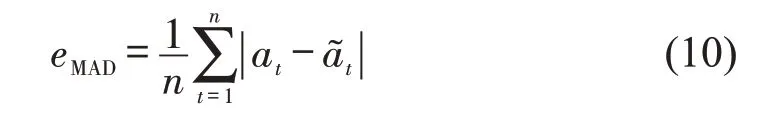
式中：n为预测时长。

3 验证与结果分析

3.1 数据采集与处理

基于实车试验采集城市快速路中驾驶人的跟驰行为数据，实验过程招募8 名熟练驾驶人，年龄介于26～46 岁之间，平均年龄为37.5 岁；驾龄介于2～26年之间，平均驾龄为10.3年。在实验前告知驾驶人注意事项，让其按照日常驾驶习惯在指定路线上自由驾驶，实验过程中被试不佩戴任何仪器，不对被试做任何干扰，确保数据真实性。实验路段为镇江市金港大道快速路基本路段，全长29 km。道路为双向8 车道，以中央隔离带分隔，限速值为100 km·h-1。实验时间避开高峰时段，安排在工作日9:00-10:30 和14:30-16:30，此时间段道路整体交通流顺畅，偶有拥堵。

实验车装配了毫米波雷达、速度传感器、视频影像传感器及GPS 等设备。毫米波雷达和视频影像传感器主要记录所感知到的周围车辆的相对距离和相对车速等交通数据信息。车辆信息数据采集系统主要由传感器采集车速和制动开度等运动参数。工控机将各路信号集中并转换，实现数据信号的同步输出。

实验采集的数据包括自车轨迹数据和车辆的周围环境数据，具体为：自车速度、前车速度、自车横摆角速度及与前车相对距离等，处理上述直接输出的数据，可以获得后续分析所需的其他数据，包括跟车时距和碰撞时间等。

跟车工况的标定通过视频查看，雷达及车辆信息采集系统数据分析共同确定。基于文献[9]的研究，本文跟车工况按照以下规则进行提取：跟车距离100 m以内，跟车时长不低于20 s，自车速度高于10 km·h-1。

在8 名驾驶人的驾驶数据集中提取2000 余组跟驰工况，经过清洗后有489600条数据，平均时长40 s。为进一步获得均衡跟驰工况下的行车数据，进一步标定跟驰数据集。在均衡跟驰工况下，跟车距离变化较小，两车车速差相对稳定，据此制定以下规则：最小安全车间距置信区间95%范围内，两车速度差小于2 km·h-1。共筛选298650 条均衡跟驰数据，占总跟驰数据的61%。

3.2 关键参数标定

对于不同数量的高斯分量，GMM-PDF 和GMM-HMM 模型的训练和测试精度不同。GMM主要用于拟合数据分布，高斯分量过少会导致对数据的拟合精度不高，无法体现完整的数据分布，过大的k值会出现过拟合问题，同时，会增加计算量和运算时间。因此，选择k∈{6,8,10,15,20,25,30,35} 获取最优k值。两个模型采用不同高斯分量数量预测的平均绝对值误差如图3所示。

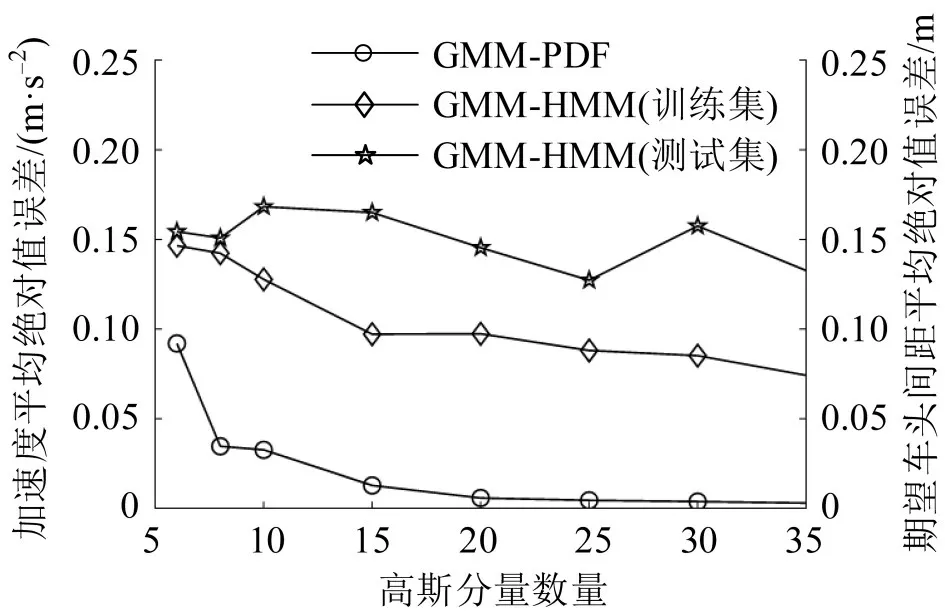
图3 不同高斯分量数量对应的平均绝对值误差Fig.3 Mean absolute deviation of different number of GMM components

由图3 可知，GMM-PDF 模型预测误差在开始时随高斯分量数量增加明显下降，高斯分量在20以后，增长趋势渐缓。k取20时，跟车距离预测误差为0.0045 m，k取25时，预测误差为0.0035 m；然而，随着高斯分量数量的增大，模型训练成本增大，k为25时的参数估计迭代时间比为20时高出2倍，综合考虑计算成本和精度，将GMM-PDF中的高斯分量数量k确定为20。

GMM-HMM 模型随高斯分量数量的增加，在训练集上的误差减小，在测试集上误差先减少后增大。因为，对训练集的预测中，过少的高斯分量数量对数据的拟合精度不高，从而产生较高的误差，随着高斯分量数量的增加，预测误差有所降低，但是，计算成本增大，并会出现一定程度的过拟合，图3 中体现为测试集预测误差增大。GMM-HMM测试集精度在k为25时最低，因此，将高斯分量数量设为25。

3.3 结果分析

3.3.1 个性化双层模型与传统模型的性能比较

本文采用遗传算法对Gipps 和ODM 模型进行参数优化标定，优化目标函数为待标定模型模拟数据与实测数据的差值，自变量为待标定参数，约束条件为各参数的取值范围，利用MATLAB 的遗传算法工具箱进行优化求解。以1 号驾驶人为例，Gipps模型标定的参数值为α=1，V=71.02，b=-1b′=-3.80；ODM 模型标定的参数值为τ=0.009，X1=42.000，X2=74.948，β=0.023，θ=1.982。以标定好参数的模型预测各样本的跟驰加速度序列，利用eMAD评价模型效果。其中，Gipps 模型预测误差为0.436 m·s-2，ODM 预测误差为0.369 m·s-2，本文提出的双层模型对1 号驾驶人的预测误差在测试集上为0.127 m·s-2，相较于Gipps 模型降低了0.309 m·s-2，相较于ODM 模型降低了0.242 m·s-2。分别使用8名被试个体跟车数据标定模型参数，得到不同模型的加速度预测误差，如图4所示。

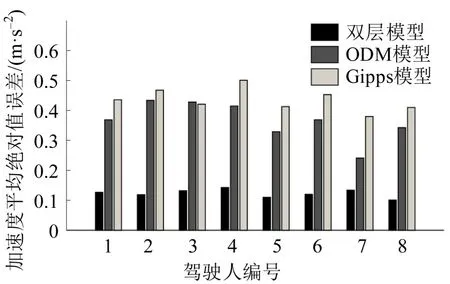
图4 不同模型的加速度平均绝对值误差Fig.4 Mean absolute deviation of acceleration for different models

由图4可知，双层模型效果最优，8位被试驾驶人在训练集上预测误差均值为0.101 m·s-2，在测试集上为0.123 m·s-2，证明了双层个性化模型在描述跟驰行为时具有更好的性能。

3.3.2 个性化双层模型和单层模型性能比较

为进一步验证个性化双层驾驶人模型在加速度预测上的优势，使用同一测试样本集对单层驾驶人跟驰模型和双层驾驶人跟驰模型进行精度测试，结果如图5所示。

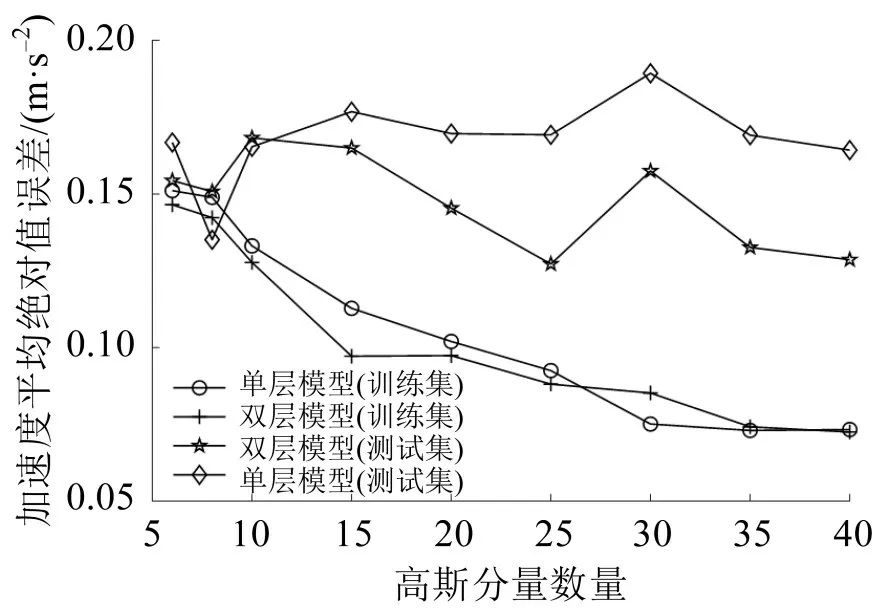
图5 双层模型和单层模型性能对比Fig.5 Comparison of model performance between two-layer model and monolayer model

由图5可知，单层模型和双层模型在训练集上预测误差较为接近，但在测试集上表现存在差异，随着高斯分量数量的增大，双层模型的预测误差明显低于单层模型，表明双层模型能更有效地预测驾驶人实际的跟车加速度。

任意两段跟车行为数据的加速度预测比较如图6所示。

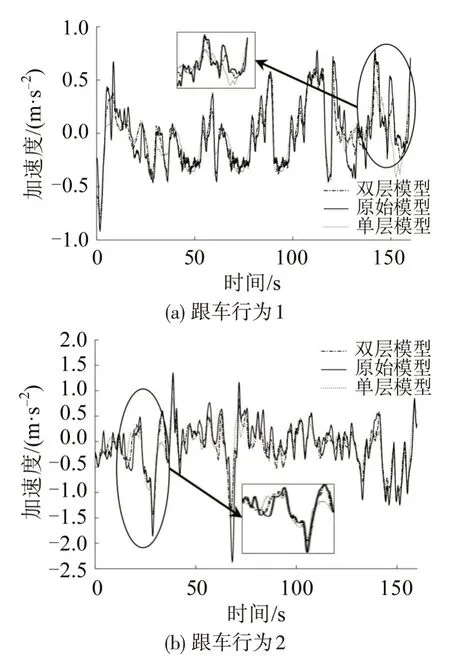
图6 双层模型与通用模型的加速度预测对比Fig.6 Comparison of acceleration prediction between two-layer model and monolayer model

图6(a)中，双层模型预测平均绝对值误差为0.087 m·s-2，单层模型为0.125 m·s-2，前者较后者，误差降低30.4%，且在峰值处单层模型精度较低；图6(b)中双层模型预测平均绝对值误差为0.096 m·s-2，单层模型为0.146 m·s-2，在0～50 s 和140～150 s 时段，单层模型的预测误差显著高于双层模型。主要原因为，测试集某些时刻的跟车样本未处于均衡跟车状态，所测得的跟车距离并不是驾驶人所期望的跟车距离，双层模型中引入期望跟车间距，预测结果更能表现驾驶人当前时刻的期望加速度值，同时表明，所提出的期望跟车距离参数的有效性。

3.3.3 个性化双层模型和通用模型性能比较

为验证驾驶人跟驰模型个性化的必要性，使用同一测试样本集在通用模型和个性化双层模型进行性能测试，结果如图7所示。

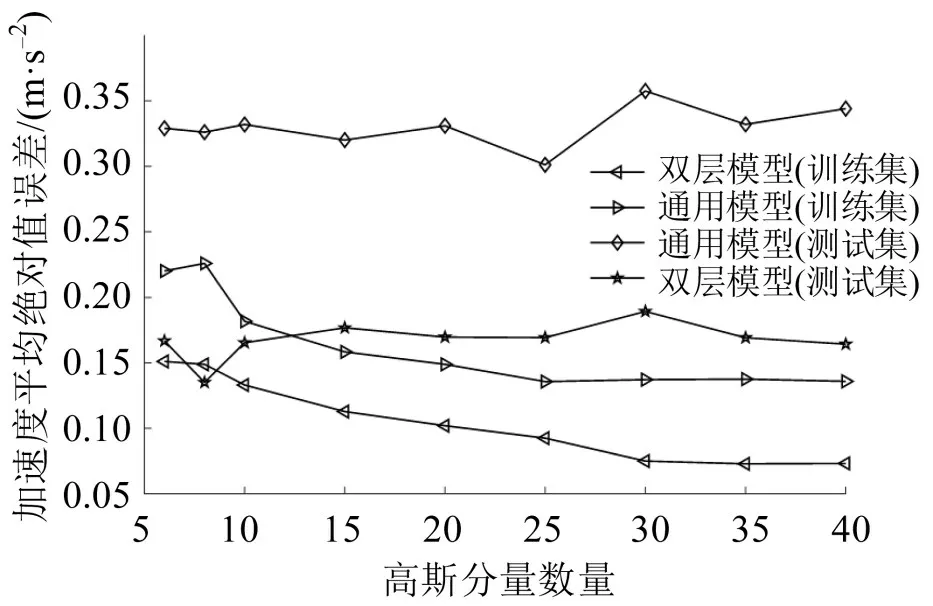
图7 双层模型与通用模型性能对比Fig.7 Comparison of model performance between two-layer model and general model

由图7 可知，在任意高斯分量数量下，个性化双层模型预测效果均要优于通用模型，通用模型在测试集上的预测精度较低。为进一步细化两个模型在预测精度上的差异，比较任意两段跟驰行为数据，结果如图8所示。

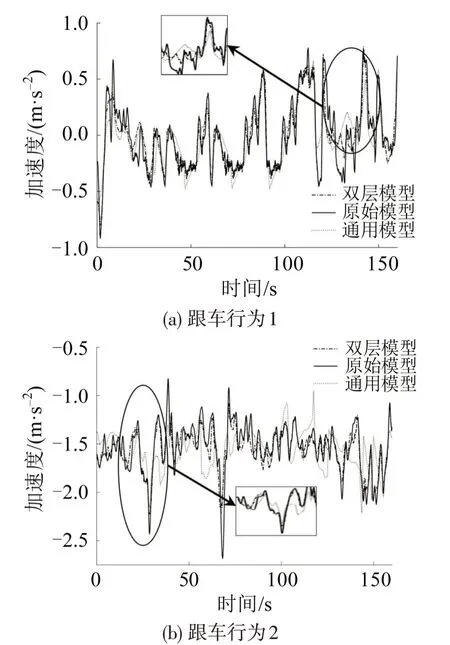
图8 双层模型与通用模型的加速度预测对比Fig.8 Comparison of acceleration prediction between two-layer model and general model

图8(a)中双层模型加速度预测平均误差为0.087 m·s-2，通用模型为0.190 m·s-2；图8(b)中双层模型加速度预测平均误差为0.096 m·s-2，通用模型为0.301。双层模型在两段数据上的精度均较高，表明驾驶人存在其独特的驾驶习惯，基于通用模型的智能驾驶系统难以满足驾驶人的个性化需求。

4 结论

(1)个性化的驾驶人跟驰模型需适应不同驾驶人的期望跟车间距和行为习惯，将期望跟车间距参数引入模型，构筑双层跟驰模型框架，采用GMMPDF 方法建立驾驶人跟车期望距离模型，基于GMM-HMM 方法学习驾驶习性，建立个性化驾驶人跟驰模型。模型具有解释性强，易于描述驾驶行为非线性和不确定性的优势，可以为智能车辆的自适应巡航系统和自动跟车系统等提供更加精准化、拟人化及符合驾驶人预期的驾驶人跟驰模型。

(2)基于自然驾驶行为实验数据的验证研究表明，所提出的自适应期望跟车间距和行为习惯的双层驾驶人跟驰模型在描述个体驾驶人跟驰行为上表现出良好的性能，与Gipps模型、ODM模型、单层模型及通用模型的预测结果对比显示，所建模型计算的平均误差绝对值优于其他模型30%以上，与驾驶人实际跟驰行为的吻合度更高。