基于网格交通状态分类的行程时间规律挖掘与计算
谢东繁,贾惠迪,李春艳,赵小梅
(北京交通大学,交通运输学院,北京 100044)
0 引言
近年来,我国很多城市机动车保有数量不断增大,城市道路交通拥堵日益加剧。据公安部统计,截至2020年6月,全国机动车保有量达3.6亿辆,城市拥堵已经成为常态。为解决交通拥堵等城市病,很多文献从交通管理与交通诱导的角度提出缓解城市交通拥堵的措施,而大量措施的基本前提是准确的行程时间估计。
道路行程时间通常受到多维度复杂因素的影响,如驾驶行为、道路属性、交通状况和信号配时等。因此,沿路段的行程时间是随机分布的,故行程时间分布是行程时间估计、出行时间变异性和行程时间可靠性研究中不可回避的问题。现有行程时间研究大多致力于寻找最佳拟合模型,拟合分布可分为单峰分布和其他分布。单峰分布多为高斯分布(Gaussian Distribution)、对数正态分布(lognormal Distribution)、伽马分布(Gamma Distribution)、韦伯分布(Weibull Distribution)和布尔分布(Burr Distribution)[1-3]。Rahman等[4]利用公交车GPS数据对行程时间进行估计时发现,对数正态分布和正态分布是拟合较好的分布。Chen 等[5]经过分析发现,在不同时段、不同星期、不同路段位置、不同天气条件下的出行时间分布更契合Burr 分布。对于其他分布,多为截尾分布和混合模型分布[6]。有研究证实混合模型对行程时间的拟合效果要优于单模型拟合[7]。Cao 等[8]将行驶时间分解为运动时间(车辆实际行驶的时间)和排队时间,使用截断分布对运动时间建模,而将排队时间用质量分布和均匀分布的混合分布表示。Samara 等[9]使用有限高斯混合模型(GMM)估算分段行程时间分布,并应用几种Copula模型进行拟合。
尽管当前已经有许多关于道路行程时间估计的研究成果,然而由于行程时间估计的多维度复杂影响因素,仍存在一些典型问题有待深入研究。首先,当前的研究成果主要从统计数据自身的角度研究行程时间分布规律,没有深入挖掘交通状态等因素对行程时间的影响机制,从而导致行程时间估计的精度不高;其次,当前研究多针对路段数据进行挖掘分析,从路网角度对行程时间进行深入研究的文献较少;此外,由于道路交通网络与交通状态的动态性与复杂性,面向大规模路网的快速行程时间估计也是富有挑战性的工作。
基于以上分析,本文面向大规模城市路网,提出基于宏观基本图理论的行程时间估计方法,得到行程时间分布函数,并进行实例验证。本文的出发点与创新之处体现在以下方面:首先,采用车辆轨迹数据标定区域网络宏观基本图模型,用于区域路网交通状态的分析与辨识;进而,在区域交通状态划分的基础上,探析不同交通状态下行程时间分布规律,验证交通状态对行程时间分布的重要作用;最后,提出考虑区域交通状态的行程时间联合概率密度模型,可以较好估计行程时间,也可以给出出行者在给定时间内到达的概率,能够为交通诱导与管控提供技术支撑。
1 基于宏观基本图的交通状态划分
本节利用出租车数据构建宏观基本图,并使用高斯混合聚类方法,以速度为特征变量将交通状态进行划分。
1.1 数据来源及描述
网络层面的交通数据是开展宏观基本图研究的基础。本文数据为北京市出租车的轨迹数据,包含大约5万辆出租车3个月的全天数据。数据由每辆出租车上的全球定位系统(Global Positioning System,GPS)设备自动采集得到,每10 s 上传一条数据,GPS数据是由一系列带时间戳的空间位置点(以经纬度表示)组成的集合。
选取北京市二环与三环之间的局部区域开展分析,具体选取区域为图1矩形方框内部区域。此区域长1.4 km,宽3.6 km。该区域有中共中央对外联络部、北京建筑大学、北京师范大学等多个文化景点,此区域毗邻北京西站、西直门等地,人群、车辆往来密度大。对区域内出租车的轨迹进行绘制,可以看出区域内所选行驶路径的基本情况。
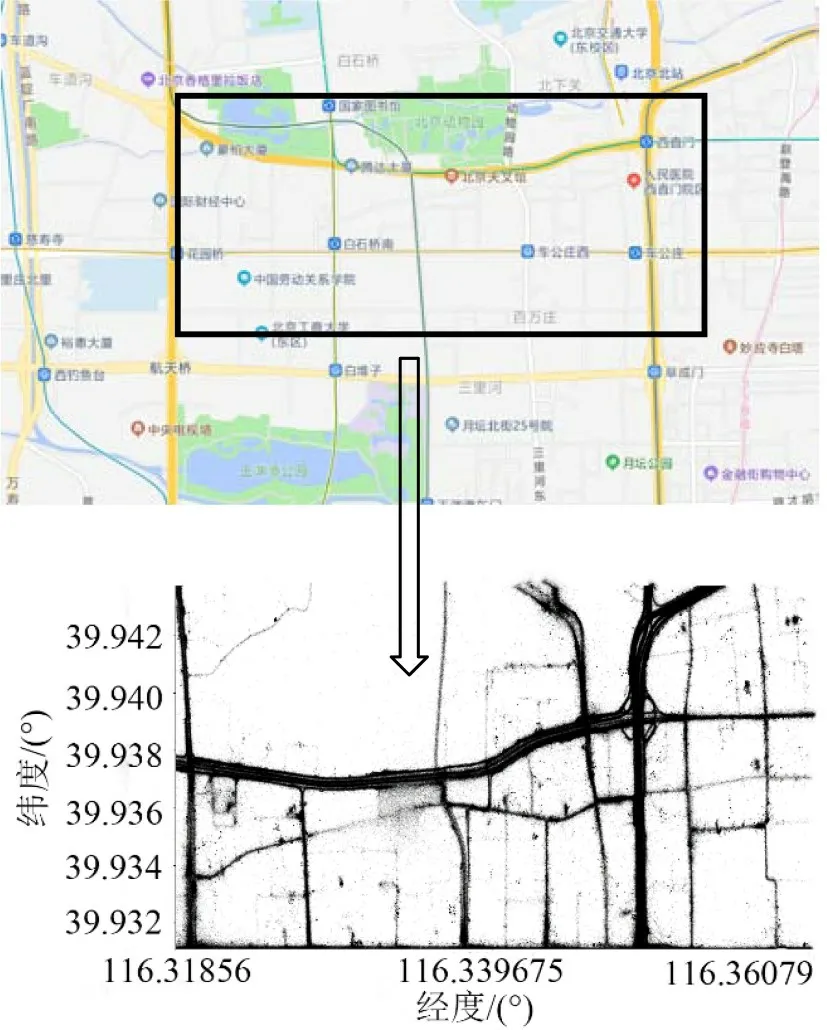
图1 所选研究区域Fig.1 Selected study area
1.2 宏观基本图构建
在城市交通中出租车与所有道路车辆的比例约为5%[10],为此难以直接基于出租车轨迹数据计算路网流量。针对此问题,宏观基本图理论中提出网络平均密度kˉ和流量qˉ的计算方法,即
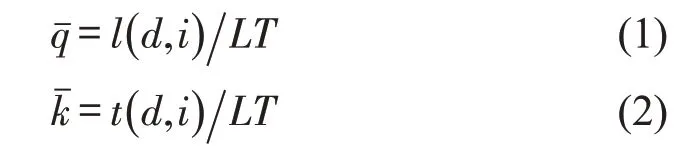
式中:l(d,i)为所有车辆在第d天第i个时段的行驶距离;t(d,i)为所有车辆在第d天第i个时段的行驶时间;L为路网中所有道路的长度之和;T为所研究数据的总时长。
在网络中,出租车交通状态变量和全部车辆交通状态变量之间的基本关系为
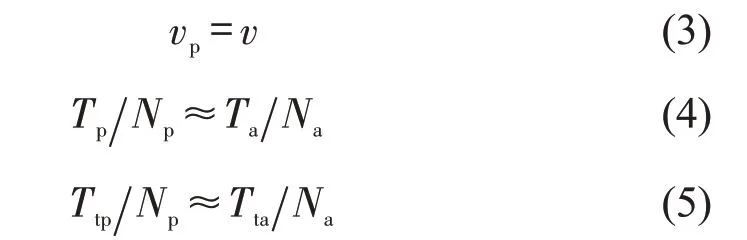
式中:vp为网络中出租车的平均速度;v为网络中全部车辆的平均速度;Tp、Ta分别为出租车、全部车辆的总行驶距离;Ttp、Tta分别为出租车、全部车辆的总行驶时间;Na为全部车辆的数量;Np为出租车的数量。
由式(3)~式(5)可知,出租车的平均行驶速度与路网中所有车辆的行驶速度近似,故用出租车的总出行时间(VKT)和总出行距离(VHT)代替式(1)和式(2)中的t(d,i)和l(d,i)构建网络基本图。为叙述方便,在后文的叙述中,流量用“总出行距离”标识,密度用“总出行时间”标识。
根据式(1)和式(2),得到研究区域的车辆密度与区域内流量的变化曲线,以及区域内车辆运行速度与区域内车辆密度的变化曲线,如图2所示。可以看出,随着路网中车辆密度的增加,平均速度逐渐下降。为更清楚地看到流量与密度随时间的变化,绘制两日的流量与密度的时间序列,如图3所示。从图中可以看出:流量与密度的变化趋势相似,工作日与周末在0:00-6:00 时段流量较低,但周末0:00附近的流量和密度要大于工作日;工作日与周末早高峰的开始时间都出现在6:00左右,从此时刻开始,流量和密度急剧增加,工作日大约在8:30左右达到最高峰,而周末的高峰一直持续到13:00左右;工作日和周末的晚高峰数值都小于早高峰,这是由于早高峰的通勤出行时段更加集中,而晚高峰对时效的要求则相对宽松。
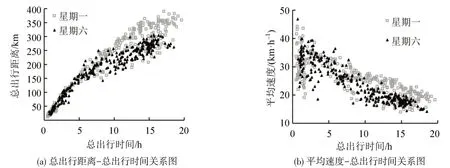
图2 工作日与周末基本图Fig.2 Fundamental diagrams of workdays and weekends
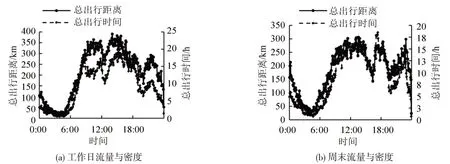
图3 流量与密度的时间序列图Fig.3 Time series of weighted flow and weighted density
1.3 基本图函数拟合
宏观基本图可以描述路网平均流量、平均密度、平均速度之间的关系。稳定的交通三参数关系是实现交通管理、交通控制和诱导的基础。因此对基本图进行拟合,通过三参数的函数关系检验研究区域交通状态的平稳性和规律性。从图2(a)可以看出,区域的流量-密度呈现抛物线的曲线关系,故在对流量-密度散点图进行拟合时,首先采用多项式函数进行拟合。
利用一元一次、二次、三次函数对研究区域工作日和周末的流量-密度基本图进行拟合,分析区域的拟合情况,如图4所示。选取R2和ERMSE作为拟合优度评价指标,R2为确定系数,通过数据的变化来表征一个拟合的好坏,正常取值范围为[0,1],越接近1,说明模型对数据拟合的效果越好。ERMSE为均方根误差,用来衡量观测值同真值之间的偏差,结果如表1所示。可以看出,无论是工作日还是周末,一元三次曲线的拟合效果均最好,结合工作日和周末的流量和密度数据来看,工作日的流量和密度跨度大于周末,相比于周末更加离散,故周末的拟合效果要显著好于工作日。因此,选择一元三次曲线作为基本图拟合函数,工作日的基本图函数和周末拟合函数分别为
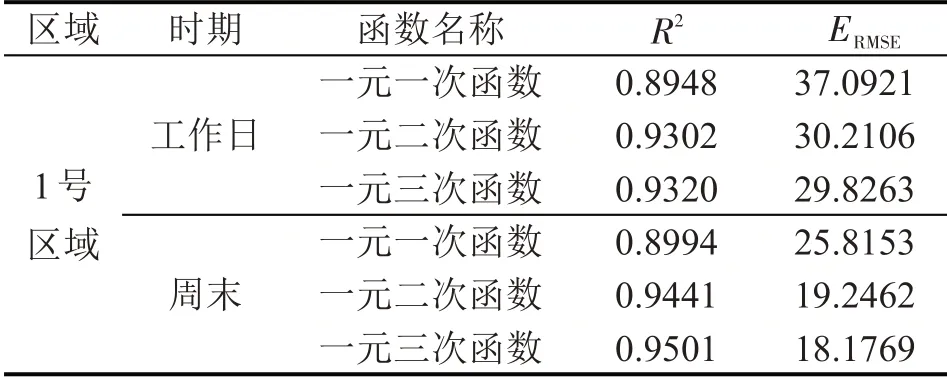
表1 拟合优度Table 1 Goodness of fitting
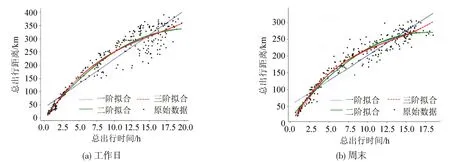
图4 基本图拟合曲线Fig.4 Fitting curves of Fundamental Diagram
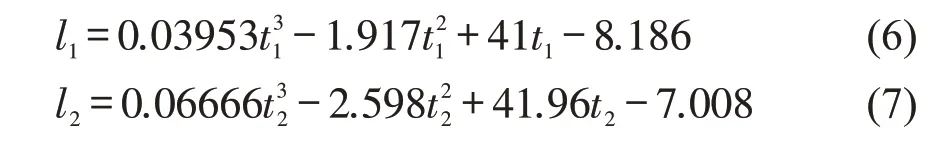
式中:l1、l2分别为工作日、周末的总出行距离;t1、t2分别为工作日、周末的总出行时间。
1.4 交通状态划分
为分析不同交通状态对行程时间的影响,首先采用高斯混合模型聚类方法对区域交通状态进行聚类分析。这是由于高斯混合模型具有一个点可以属于多个聚类,聚类形状灵活的特点;同时,由于不同路段的交通状态存在较大差别,通过高斯混合模型可以较好地表示出速度间的差异性。
根据交通流理论研究中对交通流状态的划分原则,将交通状态聚类为3类是普遍认为较为合理的交通状态划分结果[11]。为此,同样将交通状态划分为3 类,即畅通、轻度拥堵和重度拥堵,如图5所示。畅通状态表示路网中交通流在自由流范围之内,车辆能够自由行驶,车辆行驶不受或者基本不受其他车辆的影响,驾驶自由度大;轻度拥堵是指交通流进入不稳定流状态,车辆行驶不顺畅,速度受到很大约束,驾驶自由度低;重度拥堵则指交通流处于不稳定流或强制流的范围内,车辆形成队列,车辆长时间处于低速行驶状态,在道路上停停走走。
畅通状态对应于图5中倒三角形状数据点,此时道路流量低,属于自由流,汽车行驶速度高,车辆行驶不受道路上其他车辆影响。轻度拥堵状态对应于图5中叉形数据点,此状态与畅通状态相比速度有所下降,道路流量开始增多,车辆行驶开始受到其他车辆影响,逐渐出现排队现象。重度拥堵状态对应于图5 中圆形数据点,此时车速已经很低,均在25 km·h-1以下,属于饱和流,车流量也很低,道路上车辆排队拥堵成为常态。
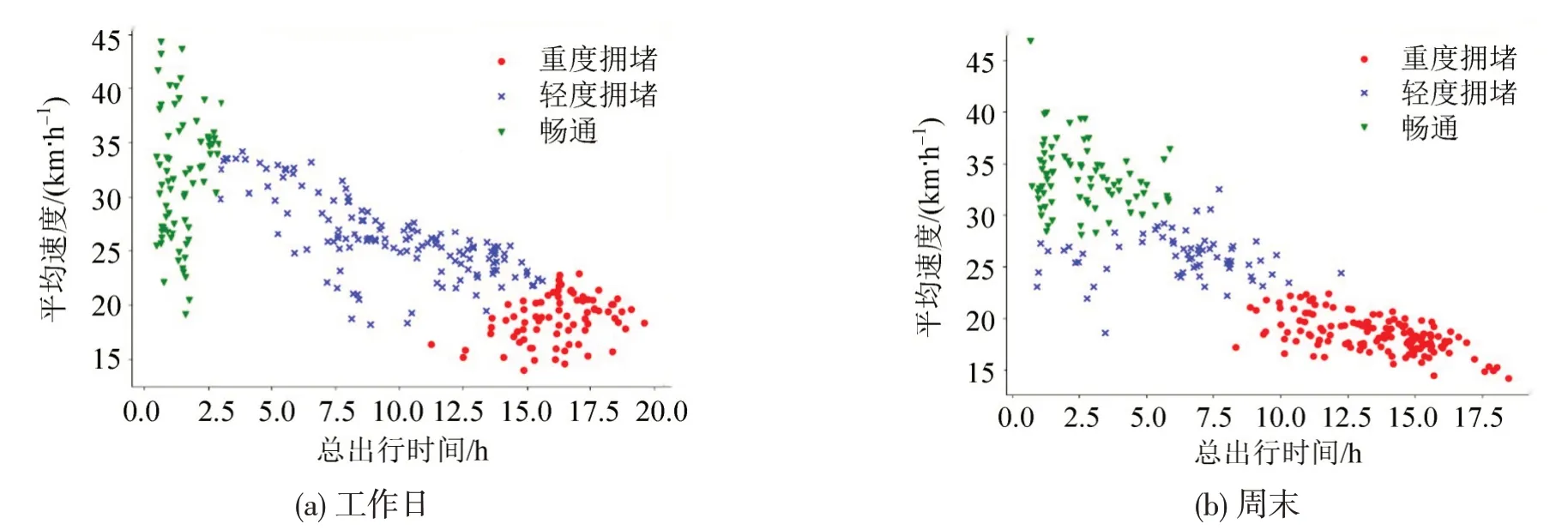
图5 区域交通状态聚类结果Fig.5 Clustering results of regional traffic states
统计分析聚类结果,得到工作日3类交通状态(即畅通、轻度拥堵和重度拥堵)对应的密度区间分别为[0.0,3.5)veh·h-1,[3.5,13.0)veh·h-1,[13.0,20.0)veh·h-1;周末3类交通状态对应的密度区间分别为[0.0,5.0)veh·h-1,[5.0,11.0)veh·h-1,[11.0,20.0)veh·h-1。根据前文拟合得到的宏观基本图曲线,通过换算速度区间大小,进而得到具体交通状态等级参数,如表2所示。
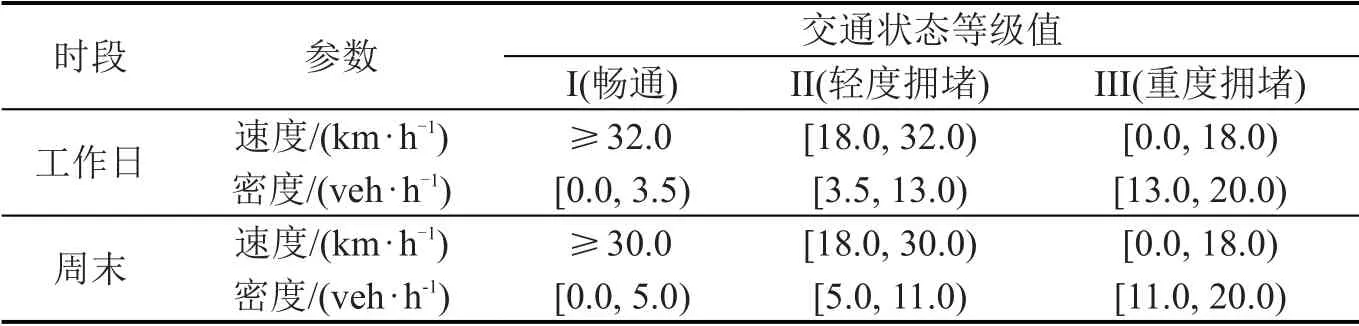
表2 区域交通状态等级聚类划分Table 2 Clustering classification of regional traffic state
2 基于网格交通状态的行程时间分布规律挖掘
当前大部分研究将轨迹数据与路网地图进行匹配之后,对行程时间的指标进行计算。然而这种方法依赖于高精度的城市矢量地图,存在研究适用性较差等问题;同时存在轨迹数据匹配计算量庞大,难以对海量数据进行实时计算等问题。为此通过构建地图网格化模型,利用出租车轨迹数据直接获取路径行程时间。
2.1 区域网格数据模型构建
在确定网长大小时,如果设置的边长过小,如几十米,可能会出现落入大多数网格的数据较为稀疏的情况;如果设置的边长过大,如500 m或以上,则一个网格可能会覆盖两条平行的道路,无法对路段进行精确分析。合适的网格大小应该保证充足的数据量且网络尽量不会覆盖两条或多条平行道路。因此,根据北京市的路网情况,将研究区域划分成均匀的边长为100 m的正方形网格,此时所选研究区域包含36×14个格子,路网的划分情况如图6所示。
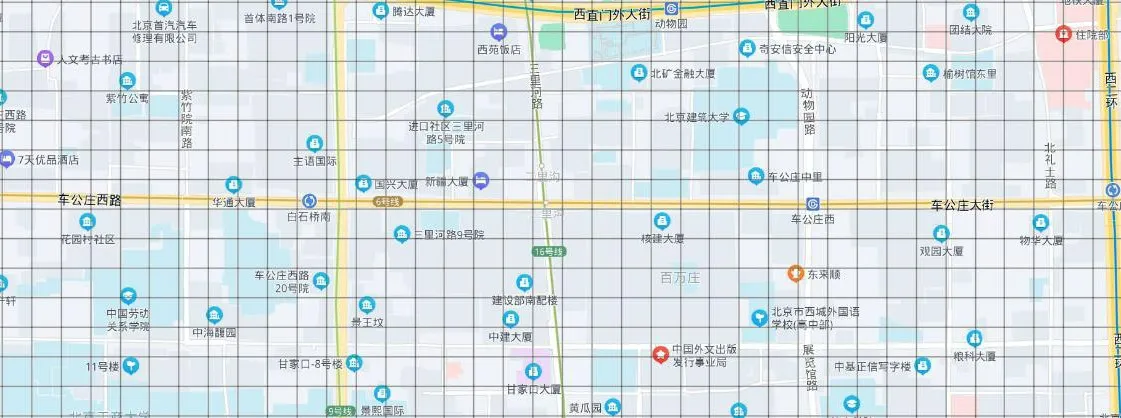
图6 研究区域划分网格示例Fig.6 A case of regional grid division
出租车数据给定了出租车的时间戳和经纬度。把每辆出租车的经纬度根据时间戳连接起来,即形成出租车的轨迹数据。因此,将某一辆出租车的轨迹点按照时间进行排列,则可得到该辆出租车的行驶路线,其平均速度为
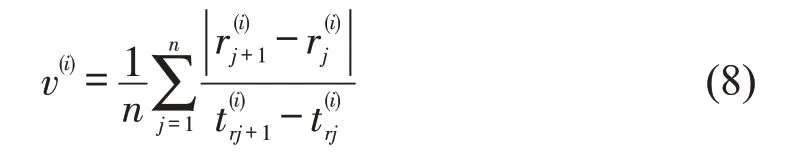
式中:n为出租车的总数;v(i)为第i辆出租车的平均速度;为第i辆出租车的第j个轨迹点的经纬度;为两个轨迹点经纬度的欧式距离;为第i辆出租车在第j个轨迹点对应的时间;为两个轨迹点的时间差。
以5 min 为间隔,求出每个网格内的平均速度后,结合表2,可以判断出每个格子所属的交通状态。
2.2 基于交通状态的网格行程时间概率密度函数
常用的行程时间分布有正态分布、对数正态分布、Weibull分布、Gamma分布、Burr分布等,选取常用的行程时间分布模型进行初步拟合,可以得到最符合分析区域内行程时间的分布。选择正态分布、t分布、指数分布、Burr分布、Gamma分布、对数正态分布、Weibull 分布和幂律分布等8 种分布进行拟合。高峰小时数据量较大,能更好地表现出行程时间分布特点,故选择7:00-8:00 的数据进行拟合,得到结果如图7所示。
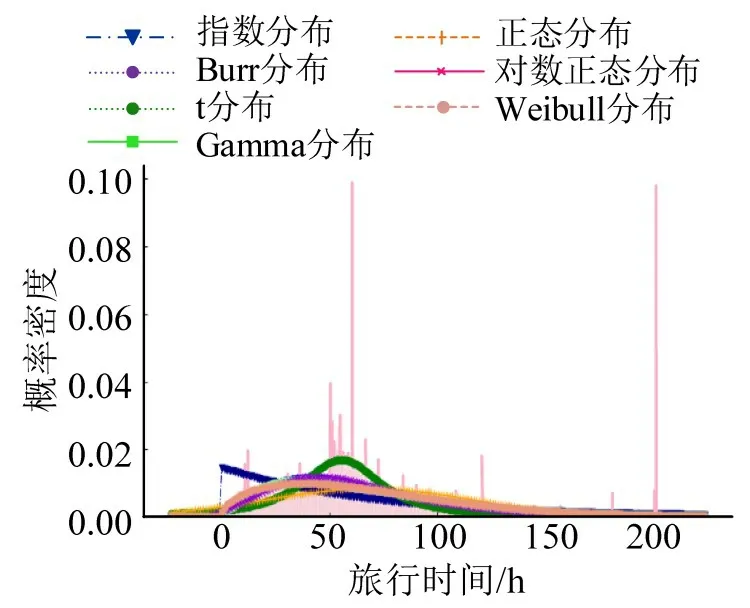
图7 不同分布模型的行程时间拟合结果Fig.7 Fitting results of various distribution models
从图7 和表3 可以看出,拟合度较高的分布有对数正态分布、Weibull 分布和Burr 分布;t 分布和正态分布无法描述出行程时间的偏态特点,幂律分布顶点处过于尖锐。为确定最佳的重度拥堵状态下的行程时间分布,对拟合p 值进行计算,p 值越大,拟合效果越好,具体结果如表3所示。选择对数正态分布、Weibull 分布和Burr 分布对15 h 的行程时间进行拟合,使用AIC 准则对结果进行对比,并引入K-S 检验方法检验模型的可行性。综合考虑两种方法的检验结果,以确定最优的分布模型进行后续分析。6:00-21:00 的拟合结果如表4所示,其中,AIC 值越小,说明拟合效果越好;K-S 检验结果中,Y 代表通过检验,N 代表未通过检验。结合表中数据可以发现,在多数时间段,对数正态分布的AIC值都是最小的,即对数正态分布的拟合效果最好,Weibull分布的拟合效果居中,Burr 分布的拟合效果较差。但在部分交通平峰时段,如6:00、15:00 和16:00 时,Weibull 分布表现出更好的拟合效果。此外,从AIC数值来看,Weibull分布与对数正态分布的结果较为接近,但在17:00 这一高峰时段没有通过K-S 检验。综上,在重度拥堵区域,对数正态分布是最理想的,可以较好地表现出行程时间的离散和左倾特点。
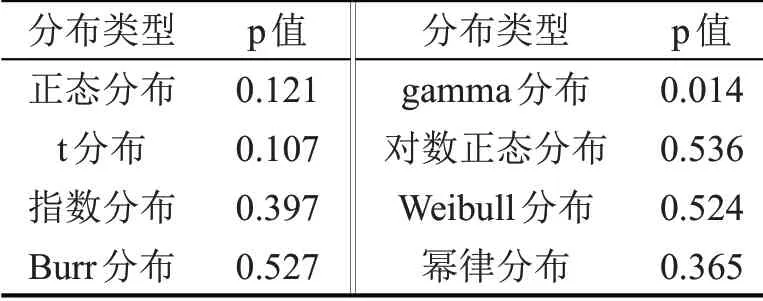
表3 各分布模型拟合p值Table 3 P value of each distribution model
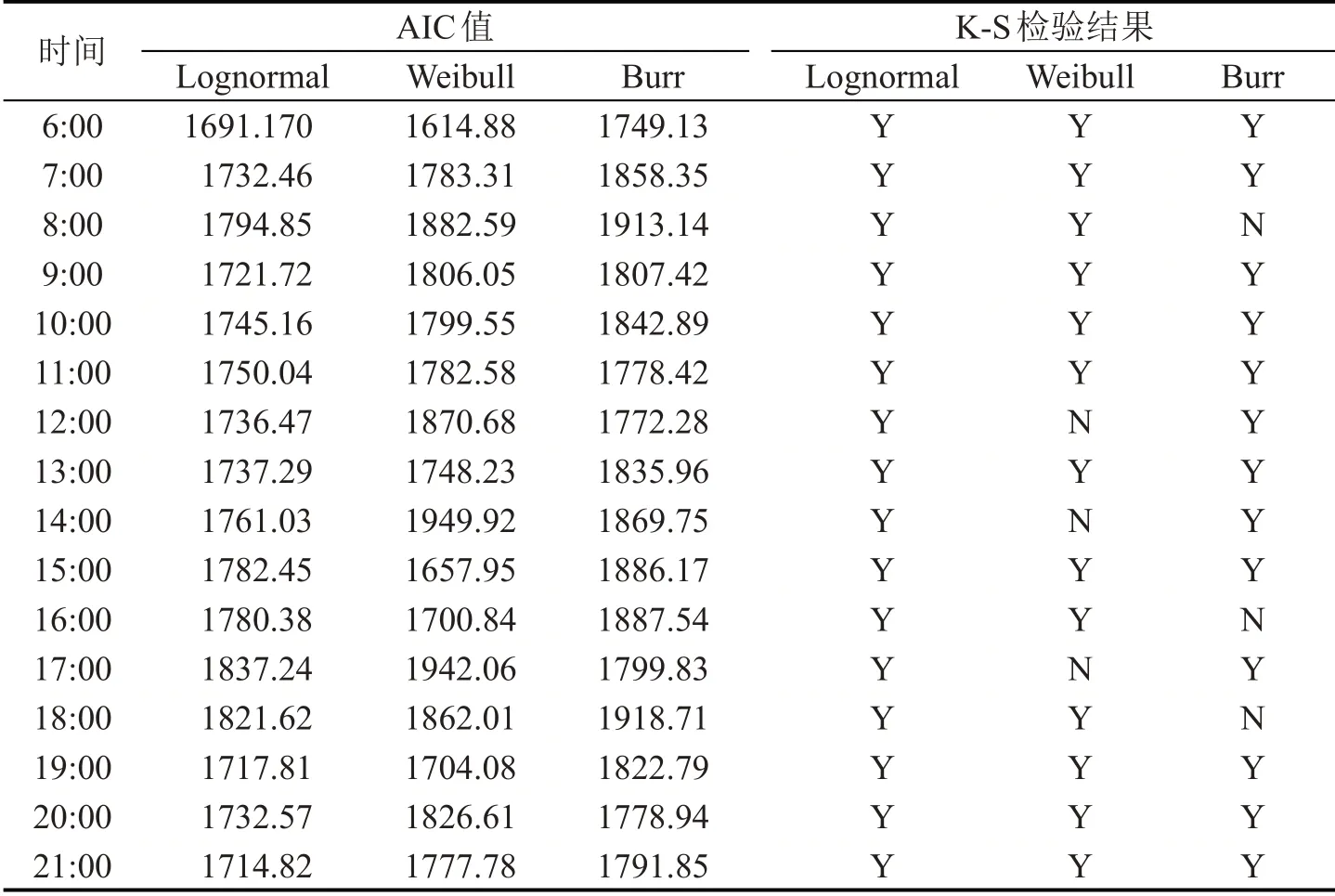
表4 各分布模型拟合检验结果Table 4 Fitting test results of each distribution model
运用同样的方法,可以对轻度拥堵状态和畅通状态的网格进行同样的概率分布模型拟合,因篇幅限制,在此不再陈述拟合过程,仅对分析结果总结如下:
(1)在畅通状态下,区域行程时间服从Gamma分布;
(2)在轻度拥堵状态下,区域行程时间服从Weibull分布;
(3)在重度拥堵状态下,区域行程时间服从对数正态分布。

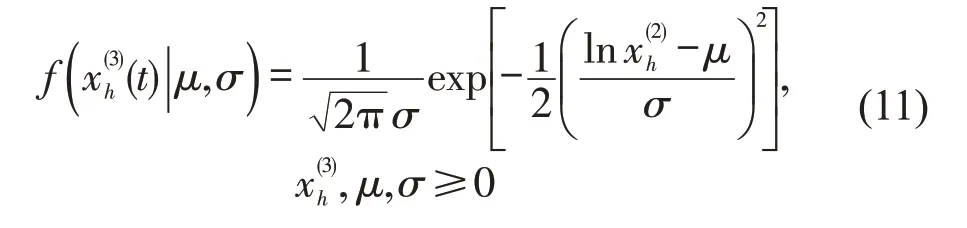
式中:α,β为Gamma 分布的参数;Γ(α)为Gamma函数;k,λ为Weibull分布的参数;μ,σ为对数正态分布的参数。
3 基于网格交通状态的行程时间概率分布模型
3.1 路径的网格行程概率分布模型
一条路径由若干个网格所包含的路段组成,一条路径的行程时间可通过各个网格内的行程时间相加得到。但各个网格的交通状态可能不同,故一条路径的行程时间分布无法通过简单的概率密度函数相加得出。
模型假设一条路径的行程时间由车辆在多个网格中行驶的行程时间组成,网格内的交通状态不同,通过网格的行程时间也具有差异,畅通状态下通过网格的行程时间服从于Gamma 分布,轻度拥堵状态下通过网格的行程时间服从于Weibull 分布,重度拥堵状态下的行程时间服从对数正态分布。假定3 种交通状态下网格内的行程时间各自对应随机变量X、Y、Z,一条路径的总行程时间为TL,则TL=aX+bY+cZ,a、b、c分别为3 种交通状态的网格数量,则总行程时间TL的概率密度函数为
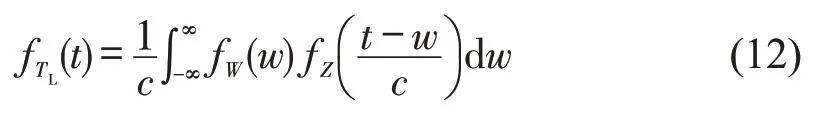
式中:w为aX与bY之和;fW(w)为w的概率密度函数;fZ(z)为z的概率密度函数。
从前文拟合得到的分布概率密度表达式来看,存在如exp(xd)的表达式,其积分不能用初等函数表示,无法用一个显式的原函数来表达,故最终的概率密度表达式无法给出显示表达。为解决这一问题,本文提出采用近似函数拟合积分函数的方法。多项式函数可以接近于任何函数,且易于积分,为此选用多项式函数近似表示难以积分的复杂函数。不失一般性,选址BP 神经网络模型进行近似函数拟合。
以研究区域中的路径1(动物园路)为例,该线路长度约为1.4 km。运用如上逼近方法求出近似表达式。在8:00-9:00 时间段内,拟合得到的λ为16.367,k为4.745,即,x取值范围为0~30,生成新的数值与原始值比较如图8所示。
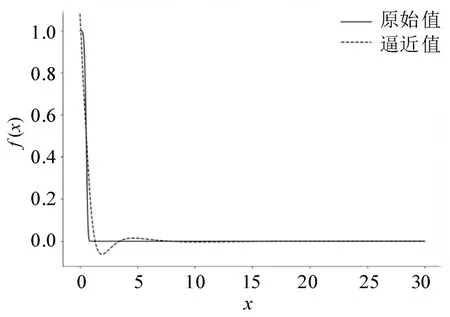
图8 原始值与逼近值对比Fig.8 Comparison of original and approximate values
为确定多项式的最佳拟合阶数,用0~20 次数进行拟合,以均方误差和R2作为选择标准,均方误差越小,R2越大,拟合效果越好,结果如表5所示。
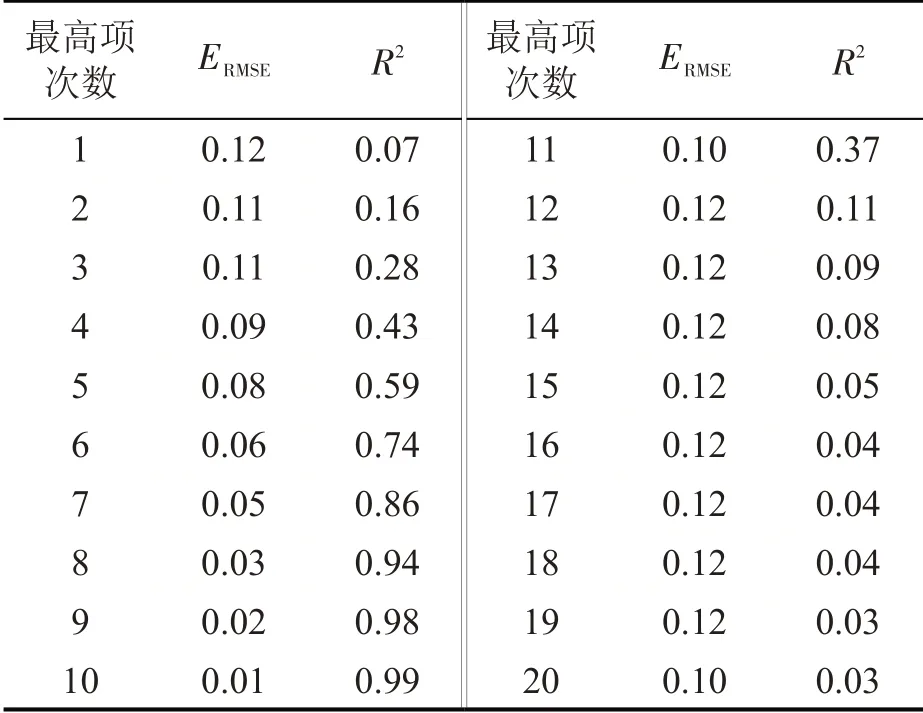
表5 0~20最高项次数拟合均方根误差及R2 变化Table 5 0 to 20 maximum terms fitting root mean square error and R2 change
结合图9和表5可以看出,在10阶时拟合效果最好。故exp[-(x/16.367)4.745]的近似表达式为
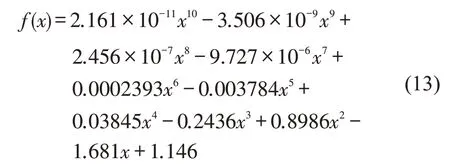
采用同种方法求得没有原函数的近似表达式后,即可求得fT(t)。仍以上述路径在8:00-9:00 时段内的行程时间为例,3 种交通状态下行程时间分布拟合得到的参数如表6所示。将参数代入fT(t)进行积分,即可求得fT(t)在8:00-9:00 时段内行程时间的概率密度函数为

表6 各分布拟合参数Table 6 Distribution fitting parameters
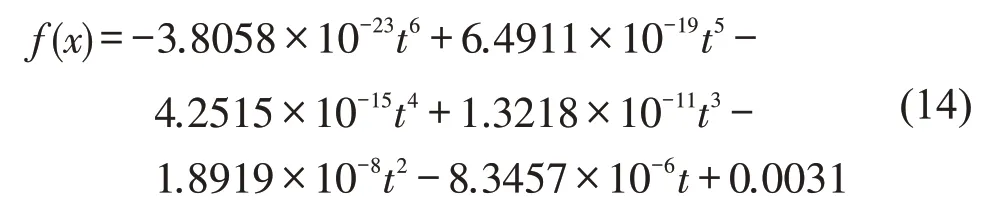
根据式(14),绘制其曲线图,如图9所示,可得在给定时间范围内完成给定行程的概率为
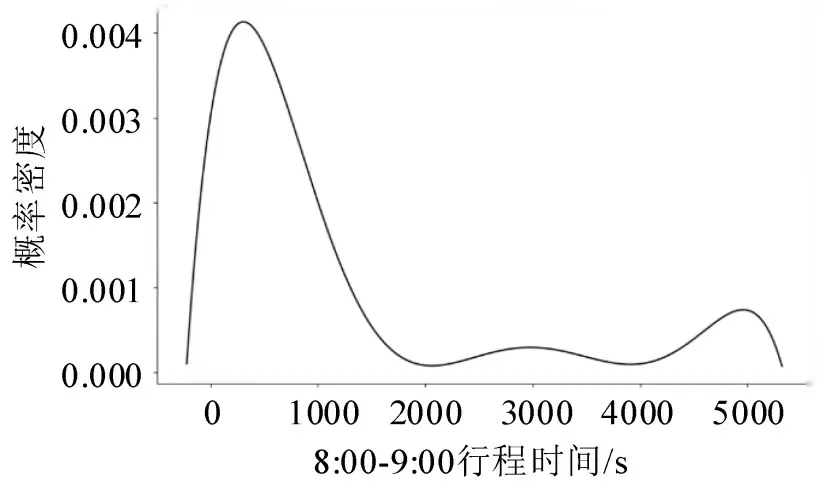
图9 选取路径1在8:00-9:00联合行程时间分布图Fig.9 Joint travel time distribution of path 1(8:00-9:00)

式中:t1、t2为一段行程的最小行程时间、最大行程时间。假设t1为0,t2为1500,则路径上的出行者在1500 s内抵达目的地的概率为80.51%;假设t1为1000,t2为1500,则路径上出行者花费1000~1500 s行程时间抵达目的地的概率为11.93%。
3.2 路径平均行程时间估计
路径平均行程时间是一个时段内经过该路径的所有车辆行程时间的平均值。根据已经得到的路径行程时间概率密度函数,可实现对行程时间变化趋势的分析。通过概率密度函数可计算其均值,即
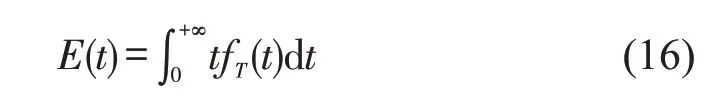
以1 h为区间,对6:00-22:00的行程时间进行估计,结果如图10所示。将真实值与估计值作对比,并计算平均绝对误差。从图10(a)可以看出,估计值与真实值的变化趋势相近,时间变化趋势也较为明显,6:00-8:00 行程时间急剧增加,8:00 时达到一天的最高峰,之后逐渐下降,并趋于平稳,直至18:00 出现晚高峰。从图10(b)可以看出,平均绝对误差的百分比都控制在1.5%~16%,表明本文提出的模型能较为准确地估计行程时间。

图10 路径1以1 h为区间行程时间估计及其平均绝对误差Fig.10 Estimation of travel time and its mean absolute error with 1 h interval in route 1
为了检验时间区间大小对行程时间估计的影响,以15 min 为区间,对6:00-22:00 的行程时间进行估计,结果如图11所示。从图11(a)可以发现,估计值与真实值变化趋势相似,与1 h 为区间的行程时间相比,一天中最大行程时间和最小行程时间都要小于以1 h 为区间的结果。对比估计精度,从图11(b)可以看出,以15 min 为区间的平均绝对误差范围控制在2.5%~12.0%,精度略高于以1 h为区间的情况,估计的行程时间值更为接近真实值。
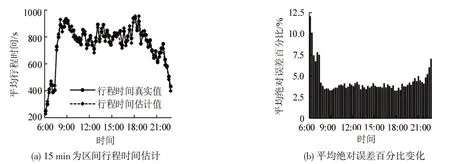
图11 路径1以15 min为区间行程时间估计及其平均绝对误差Fig.11 Estimation of travel time and its mean absolute error with 15 min interval in route 1
为进一步检验估计的有效性和适用性,选取区域内的路径2(车公庄西路)进行估计,该路径长约3.6 km。同样分别以15 min 和1 h 为区间,对6:00-22:00的行程时间进行估计,结果如图12和图13所示。可以看出,以15 min为区间估计的平均绝对误差百分比在1%~10%,要优于以1 h 为区间估计的4%~11%。对比路径1和路径2的平均绝对误差,发现路径2 的估计误差值要略小于路径1,这是因为路径2的长度要长于路径1,数据量更多。
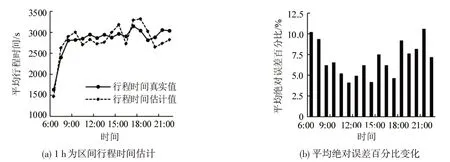
图12 路径2以1 h为区间行程时间估计及其平均绝对误差Fig.12 Estimation of travel time and its mean absolute error with 1 h interval in route 2

图13 路径2以15 min为区间行程时间估计及其平均绝对误差Fig.13 Estimation of travel time and its mean absolute error with 15 min interval in route 2
4 结论
针对现有城市路网中行程时间估计计算量大、未考虑交通状态影响等问题,本文提出基于道路网络宏观基本图理论的区域交通状态分析方法与行程时间估计方法,该方法既可以计算路径行程时间的可靠性,又可以提供给出行者在一定时间内到达的概率。主要研究方法与结论如下:
(1)基于出租车数据,应用高斯混合聚类方法,将网格交通状态划分为3类。针对3类区域进行行程时间分析发现,不同交通状态下区域行程时间服从不同的分布函数,在畅通、轻度拥堵和重度拥堵状态下,行程时间分别服从Gamma 分布、Weibull分布和对数正态分布。
(2)提出路径行程时间联合概率密度模型,即可以计算路径的行程时间的可靠性,还可以提供给出行者在一定时间内到目标区域的概率。
(3)经数据验证,模型的绝对误差百分比可以控制较小范围,可以较为准确地对行程时间进行估计,且计算速度快。
本文只考虑了交通状态对行程时间的影响,未考虑对行程时间影响的更多复杂因素,如节假日、天气等;在对路网进行网格划分时,选取标准的正方形,实际情况中,城市的规划布局有所不同,正方形在一些条件下无法精确表示道路特征;从行程时间估计的精度来看,提出的模型尚有一定提升空间。在后续研究中,将对这些内容进行更加深入细致的研究。

