出租车超速行为道路因素随机系数空间模型构建

刘海玥，蒋朝哲，付川云，周悦

(1.西南交通大学，交通运输与物流学院，成都 611756；2.哈尔滨工业大学，交通科学与工程学院，哈尔滨 150090)

0 引言

超速驾驶是我国常见的交通违法行为，其增加了交通事故发生频率，也加剧了事故发生后人员的伤亡程度[1]。出租车是超速驾驶的高发群体[2]，严重威胁了道路使用者人身财产安全。遏制出租车超速行为的发生对道路交通安全具有积极意义。

遏制超速行为离不开对其形成机理的研究。为此，大量研究挖掘出租车超速行为的诱因。目前，已证实人口统计因素和驾驶人行为特征等因素会显著影响该群体超速行为。此外，不少针对通用车辆的研究证实道路环境会显著影响车辆的超速行为，并认为车辆超速频次在限速较低[3]、无人行道和自行车道[4]以及车道数较少[5]的道路上更高。道路特征因素是影响超速行为的重要因素类型；然而，尚不清楚这类因素是否能用于解释出租车超速行为。

除以上出租车超速研究的不足，已有车辆超速行为研究普遍存在3个问题：一是少有研究讨论超速特征建模的空间相关性差异。ZIAKOPOULOS[6]研究表明，驾驶行为普遍受空间相关性的影响，忽略相关效应会导致分析结果出现较大偏差。交通领域常用的空间模型包括空间条件自回归和空间同步自回归等。QUDDUS[7]研究指出，空间模型的恰当选用对提高模型拟合能力有着显著作用。不同的研究对象将导致适用空间模型改变。目前，尚缺乏对于特定超速特征适用的空间模型的相关讨论。二是现有超速行为研究多以超速频次为研究对象[8]，将不同严重度的超速行为记为同等权重的离散数据进行分析，难以客观反映诸如轻微超速和严重超速等某些特定超速事件的行为特征。三是当前超速行为研究普遍未能考虑样本异质性对估计结果的影响。例如，BALASUBRAMANIAN 等[9]和MORADI等[10]采用固定系数和效应的logistic回归模型，在假定因素估计系数对各样本影响一致的基础上，分析超速行为。然而，宋栋栋等[11]研究发现，个体样本受不同因素的响应存在差异，并建议采用随机系数建模方法。但是，相关工作尚未在超速研究中进行尝试，超速样本的异质性问题有待于进一步探索。

综上，本文以出租车GPS 轨迹数据为数据基础，搜集道路特征信息作为潜在影响因素；并以出租车路段超速线密度及超速严重度作为研究对象，将超速线密度划分为总体超速线密度和严重超速线密度，将超速严重度划分为最小超速严重度、最大超速严重度及5%，10%，90%，95%位超速严重度；在考虑空间效应和组间异质性的基础上，构建空间条件自回归模型和空间同步自回归模型，确定出租车超速线速度和超速严重度各自的最优模型类型，并识别两者各自的显著影响因素。研究确定了建模不同超速特征所适用的拟合模型，并揭示了道路因素对出租车超速行为的影响机理，为出租车超速行为干预提供依据。

1 数据描述

1.1 研究范围

本文选取四川省成都市中心城区作为研究区域。提取2016年11月1～14日该区域出租车行驶GPS 轨迹点。数据记录点的间隔为10 s。根据GPS 轨迹点的覆盖情况，选取轨迹较多的43 条主干道(共256条路段)作为研究单元。所选道路如图1所示。

1.2 GPS轨迹数据处理与超速轨迹识别

采用地图匹配算法修正因信号干扰而导致定位误差的GPS 点位置。即分析脱离道路轨迹点的位置与邻近道路坐标，将所有定位误差轨迹点匹配至车辆行驶时所在的道路中心线上，并剔除交叉口30 m 以内的轨迹点和因调头和逆行等异常驾驶行为生成的行驶轨迹点。余下GPS 轨迹点用于超速行为识别。超速轨迹识别的具体步骤如下。

Step 1 计算平均速度，其表达式为

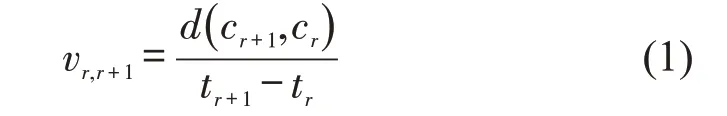
式中：vr,r+1为第r个GPS轨迹点到第r+1个GPS轨迹点间出租车车辆的平均速度；cr+1、cr分别为第r+1 个、第r个GPS轨迹点所在地理位置；d(·)为两点间距离；tr+1、tr分别为第r+1 个、第r个GPS 轨迹点的定位时间。

Step 2 将平均速度vr,r+1与轨迹点所在道路s的限速值Vs比较，以识别超速行为。若vr,r+1＞Vs，则认为这对轨迹点(r,r+1)是一段超速轨迹。据此识别出所有出租车在研究路段内的超速轨迹。若一段超速轨迹是孤立的，则认为其是1起超速行为；若多段超速轨迹彼此相连，则合并为1 起超速行为。

考虑到GPS点定位存在误差，对匹配后得到的出租车超速行为进行误差检验。证实正确识别超速行为的概率在限速值为40 km·h-1和限速为60 km·h-1的道路上分别为94.03%和93.66%，超速行为及轨迹识别具有较高的识别精度。

1.3 总体超速线密度与严重超速线密度

在城市路网中，较长的路段因其容易汇聚更多车辆，往往也伴随着更多频次的交通违法行为，因此，在不考虑暴露量的情况下直接研究超速频次可能无法客观反映道路因素对出租车超速行为的影响。因此，本文提出单位长度(km)路段上超速频次的概念，即以道路长度作为暴露量，计算其超速线密度，计算式为

式中：ps为路段s的出租车总体超速线密度；Cs为路段s在14 d内发生的所有出租车超速行为总数；ls为路段s的长度(km)。

值得注意的是，高范围超速行为对交通安全的威胁更大。根据《中华人民共和国道路交通安全法(2021 版)》中对超出道路限速20%及以上的行为进行的罚分处理，可将超速范围大于等于20%的超速行为视为严重超速行为。本文同步考虑出租车严重超速行为，其线密度计算公式与出租车总体超速线密度类似。

1.4 超速严重度

除超速频次外，同时分析路段的出租车超速严重度，计算式为

式中：Bs,c为路段s上14 d 内发生的第c起超速行为对应的出租车超速严重度；vs,c为路段s上发生的第c起超速行为的出租车行驶速度。

分别将各路段的超速严重度按照升序排列，筛选出各路段14 d 内的最小、5%位、10%位、90%位、95%位及最大超速严重度。将最小、5%位、10%位超速严重度视为低超速严重度；将90%位、95%位及最大超速严重度视为高超速严重度，分别建模探究高低分类中全部百分位数超速严重度的道路影响因素。

1.5 道路因素

本文涉及43 条道路的256 条路段。路段可定义为相邻交叉口之间的道路段或道路上某段相对于其他段，任意一种道路特征不同。对于后面一种定义，可能改变的道路特征包括：路段限速值、路段车道数、横断面形式、非机动车车道及公交专用道等。同时，这些特征也作为可能的影响因素用于后续建模。此外，本文还筛选了其他交通管理与道路特征作为因素，包括路段的超速抓拍摄像头数，是否为单行道，是否存在上下坡匝道，是否存在路段施工区及路段长度等。共采用10 个道路特征因素，各变量的描述如表1所示。

表1 关键变量描述Table 1 Description of key variables

2 空间相关性判定与模型构建

模型构建前，为避免空间相关性对分析结果的影响，采用全局Moran′sI指数对出租车超速线密度和超速严重度的空间相关性进行检验。检验发现，总体超速线密度与严重超速线密度对应的Moran′sI指数分别为0.470 和0.506；最小、5%位、10%位、90%位、95%位和最大超速严重度对应的Moran′sI指数分别为0.148、0.344、0.344、0.441、0.441和0.541。所有Moran′sI指数检验结果表明，出租车超速线密度和超速严重度在95%置信区间下均存在显著的空间聚集效应，建模中需考虑空间自相关效应的影响。

基于高斯分布的广义线性模型是连续变量建模最为常用的统计模型，被广泛应用于事故率和车辆速度特征等连续变量研究。为了减少数据异方差性，采用对数-高斯模型分别对超速线密度和超速严重度进行建模。同时，根据空间莫兰指数分析结果，在考虑空间相关性效应的基础上，分别构建超速线密度和超速严重度的空间条件自回归模型与空间同步自回归模型。其中，空间同步自回归模型包括空间滞后模型及空间误差模型。

2.1 空间条件自回归模型

对数-高斯的空间条件自回归模型假设目标空间效应受相邻分析单元误差的条件加权影响，即

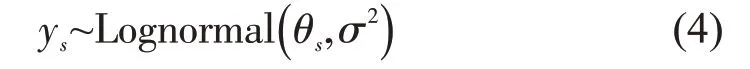
式中：ys为第s条路段的出租车超速线密度或超速严重度；θs为第s条路段的出租车超速线密度或超速严重度高斯分布期望值；m为因素个数；β0为截距项；xks为路段s的第k个变量；βk为第k个变量对应的系数；σ2为正态分布的方差，且σ～cauchy(0,2)；φs为模型捕捉的路段空间相关效应。

进一步地，因本文路段归属于若干道路，为捕捉不同因素因道路差异而导致研究路段存在的组间异质性，将其中部分因素系数考虑为组间随机系数，构建随机系数空间条件自回归模型为

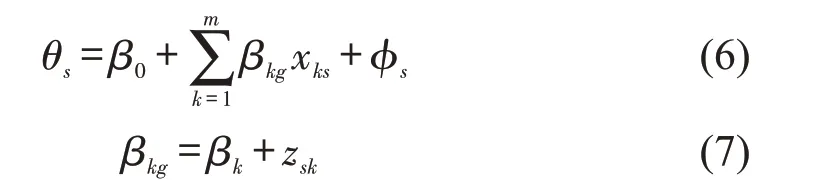
式中：βkg为第g条道路上第k个因素对应的组间随机系数；zsk为组间随机系数βkg的随机误差。

2.2 空间滞后模型

空间滞后模型假设目标研究单元的空间相关性来源于相邻研究单元因变量滞后的影响，其随机系数模型为

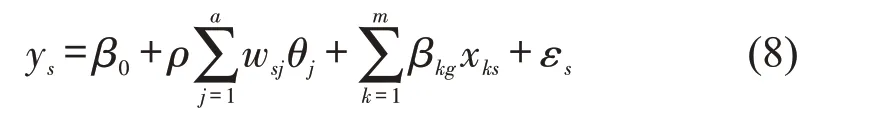
式中：ρ为空间滞后系数；wsj为空间权重关系；a为与路段s相连的路段个数，εs为路段s相关残差，。

2.3 空间误差模型

空间误差模型关注于相邻空间单元误差项间的空间关系，并以空间误差项的形式计入方程，其随机系数模型为

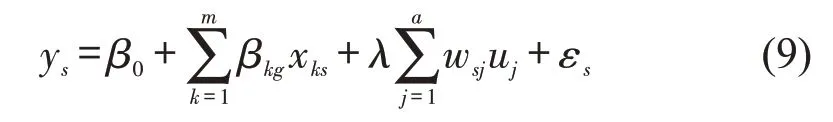
式中：λ为空间误差系数；uj为与路段j相关的随机误差项。

3 模型参数估计结果分析

分别以因变量服从对数-高斯分布的形式，构建出租车超速线密度和超速严重度的随机系数空间条件自回归模型、随机系数空间滞后模型及随机系数空间误差模型。为比较模型优劣并避免空间效应系数或组间随机系数存在不显著的情况，分别构建超速线密度和超速严重度的无空间效应标准线性模型，以及系数固定的空间模型。所有模型参数估计均基于贝叶斯推理方法，并采用双马尔科夫链和NUT 采样器(No-U-Turn Sampler)进行参数估计。估计过程设置迭代2 万次，对前1 万次迭代结果进行退火处理，以剩余1万次迭代结果得到的后验分布获取参数估计。不同模型间的拟合效果比较使用渡边-赤池信息准则(The Watanabe-Akaike Information Criterion,WAIC)。WAIC 值越小，模型拟合程度越高，且对数据信息的利用效率越高。

3.1 超速线密度空间模型参数估计

出租车总体超速线密度和严重超速线密度模型的拟合效果比较如表2所示。

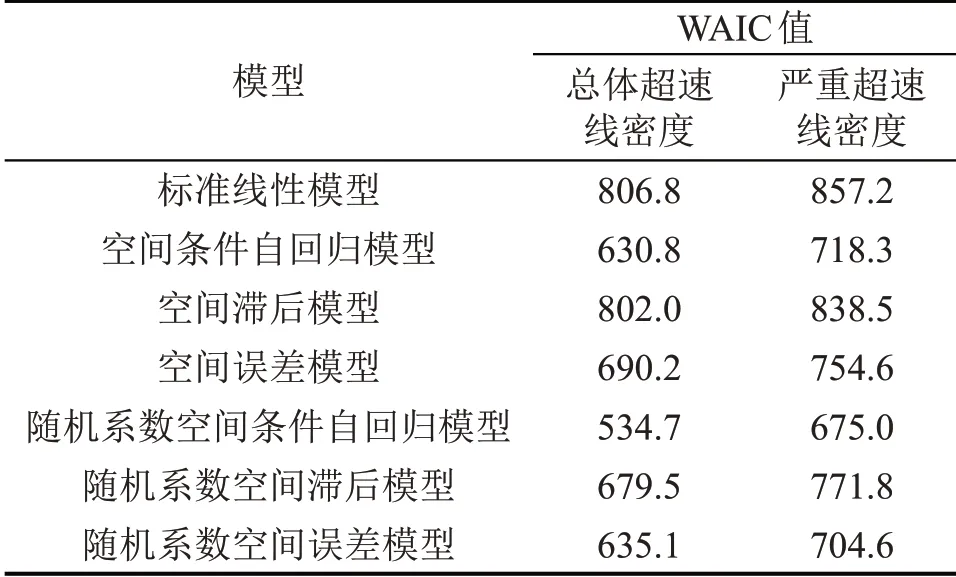
表2 超速线密度模型拟合效果比较Table 2 Comparison of model fitting for speeding linear density

7 类模型中，无空间效应的标准线性模型WAIC 值最大，说明考虑空间效应的模型拟合效果更优。所有无随机系数的空间模型中，空间条件自回归模型拟合的WAIC 值最小(总体超速线密度WAIC 值为630.8，严重超速线密度WAIC 值为718.3)，说明该模型更适合于超速线密度的空间效应建模。此外，考虑随机系数各空间模型的WAIC值均小于其对应的固定系数空间模型，表明考虑因素系数的组间异质性有助于提高模型拟合效果。所有模型估计效果表明，随机系数空间条件自回归模型WAIC 值最小(总体超速线密度WAIC 值为534.7，严重超速线密度WAIC 值为675.0)，模型拟合效果最优。因此，选择随机系数空间条件自回归模型用于揭示各道路特征因素对出租车总体超速线密度和严重超速线密度的影响。总体超速线密度参数估计结果如表3所示。

表3 两类超速线密度空间模型参数估计结果Table 3 Estimation results of spatial model for two types of speeding linear densities

由表3可知，路段限速小于60 km·h-1，存在非机动车车道及存在路段施工区这3 类因素与总体超速线密度呈正相关，而路段横断面为一块板与总体超速线密度呈负相关。路段限速的影响可以解释为，在非拥堵情况下，限速越低，出租车驾驶人越难以达到自身理想行驶速度，超限可能性越大。一块板横断面的路段意味着未设置中央隔离带，无法有效减少与对向车流间的干扰或冲突，迫使出租车必须以较低速度行驶，减少了超速行为发生的可能性。路段存在非机动车车道可以对机动车和非机动车进行有效分流，减少彼此间的相互干扰，提高出租车行驶速度，导致出现超速行为。此外，存在施工区的路段上超速线密度更高，可能与施工管理方式有关，为了保证施工区人员安全，施工时期路段限速通常较低(小于20 km·h-1)且存在大量遮挡和不规范的交通组织，使得包括限速标志牌在内的许多交通信息常常难以被出租车驾驶人第一时间观察到，容易因忽略限速而发生超速行为。

总体超速线密度得到的估计中有3 个变量出现了组间随机系数，分别为：路段限速指标、路段横断面指标及非机动车车道指标。组间随机系数的估计说明，当路段所属道路限速小于60 km·h-1时，该路段有7.45%的可能性使出租车的超速距离百分比降低(等于以2.552 为均值，1.768 为标准差的正态分布小于0部分的比例，其他随机系数的估计异质性计算类似)；此外，道路存在非机动车车道的路段时，有3.87%的可能性减少路段的总体超速线密度；对于道路中存在一块板横断面路段的情况，该道路有11.92%的概率增加路段的总体超速线密度。

严重超速线密度的模型估计结果可以看出，路段限速小于60 km·h-1与严重超速线密度显著正相关，路段横断面为一块板与严重超速线密度显著负相关。路段限速越小，出租车驾驶员越可能不满足于当前限速，发生严重超速行为可能性越大。同时，一块板横断面的路段无法对对向车流有效分流，导致在该路段行驶的出租车为规避冲突而减速刹车，减少严重超速行为的发生概率，相关分析结论与总体超速线密度结论相似。此外，路段限速指标及路段横断面指标均存在组间异质性，说明限速值小于60 km·h-1的路段所属的道路有1.64%的可能性使其路段的严重超速线密度降低；道路存在一块板横断面路段时，有15%的概率使其路段的严重超速线密度增加。

3.2 超速严重度空间模型参数估计

低超速和高超速严重度空间模型的拟合效果如表4所示。

表4 超速严重度模型拟合效果比较Table 4 Comparison of model fitting for speeding severity

由表4可知，空间效应模型拟合优于非空间模型，且空间滞后模型对5%位、10%位和90%位超速严重度均有更好的拟合效果；空间条件自回归模型和空间误差模型分别对最小超速严重度和95%位超速严重度具有更好的拟合效果；随机系数空间条件自回归模型对最大超速严重度拟合最好。

低超速和高超速严重度最佳模型的参数估计结果如表5所示。由表5可知，对于低超速严重度，路段限速指标、非机动车车道指标和路段长度均显著，但其系数较小，表明道路因素对低超速严重度的影响不明显。对于高超速严重度，路段限速小于60 km·h-1增加90%位、95%位和最大超速严重度，而路段存在施工区仅与90%严重度负相关，路段长度仅与最大超速严重度正相关，表明施工区和路段长度的影响在不同超速严重度间存在差异。此外，对于最大超速严重度，路段限速指标的系数为随机系数，表明限速值小于60 km·h-1的路段所属的道路有约3%的可能性降低最大超速严重度。

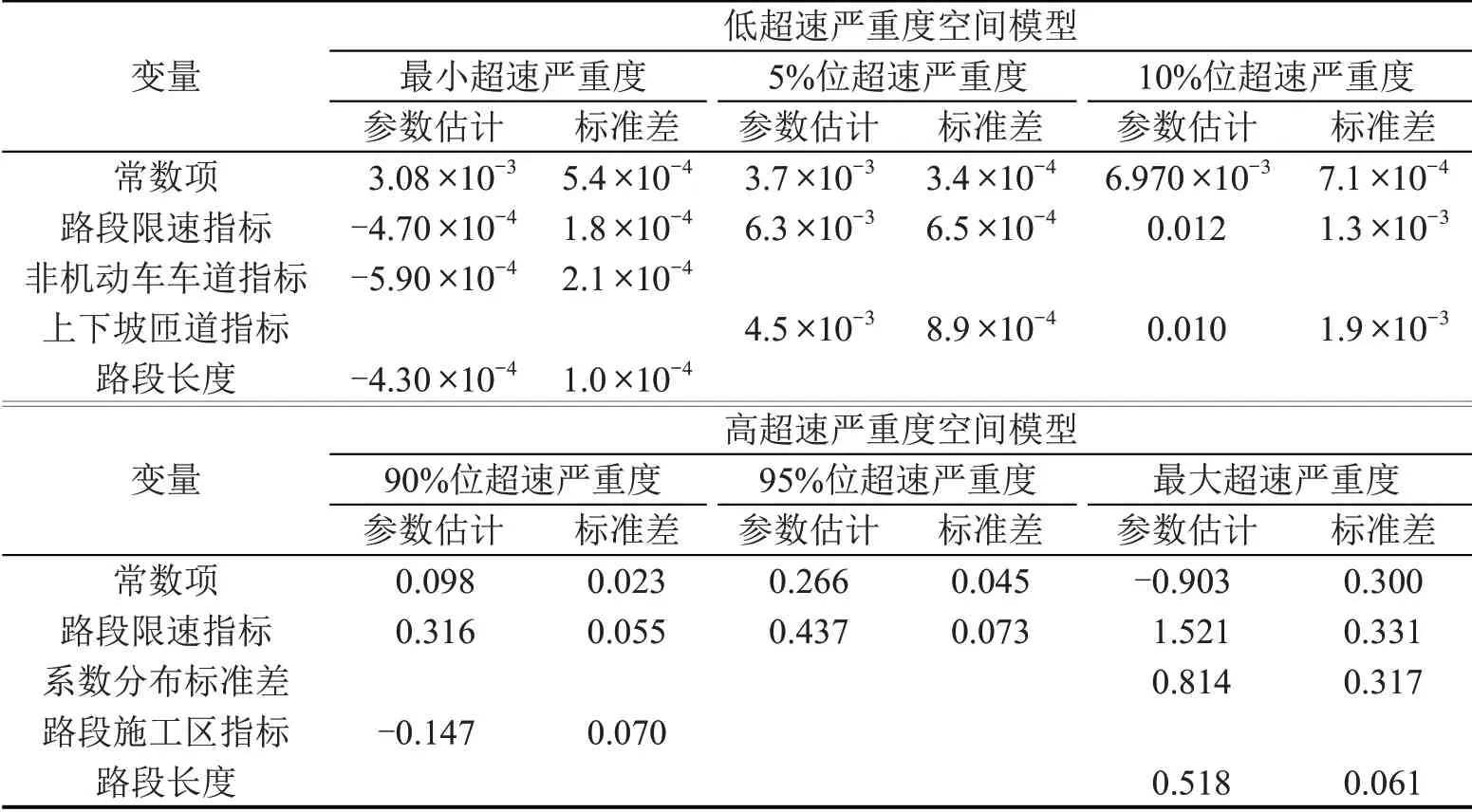
表5 超速严重度空间模型参数估计结果Table 5 Estimation result of spatial model for speeding severity

4 结论

本文讨论了道路因素对出租车路段超速线密度和超速严重度等两类超速行为特征的影响，得到如下结论：

(1)路段的超速线密度及超速严重度均存在显著的空间相关性(聚集)，考虑空间效应的模型拟合效果优于无空间效应的模型。不同出租车超速特征的空间相关性类型不同，其最优拟合模型也存在差异。具体而言，随机系数空间条件自相关模型为总体超速线密度、严重超速线密度和最大超速严重度的最优模型；空间条件自回归模型是最小超速严重度的最优模型；空间误差模型为95%位超速严重度最优模型；空间滞后模型对其他百分位数超速严重度拟合效果最好。

(2)路段限速、一块板横断面及非机动车车道这3个因素系数出现估计不一致，表现出其对超速行为特征的组间影响异质性。因素解释方面，对超速线密度，非机动车车道和道路施工区显著增加路段总体超速线密度，路段限速小于60 km·h-1显著增加总体和严重超速线密度；对超速严重度，道路因素显著影响高超速严重度，但对低超速严重度影响不大。路段限速小于60 km·h-1显著增加90%位、95%位和最大超速严重度；路段长度与最大超速严重度正相关。