考虑边界条件不确定性的城市交通拥塞风险分布迁移规律研究

胡立伟，赵雪亭

(昆明理工大学，交通工程学院，昆明 650500)

0 引言

城市路网交通拥塞严重影响居民的出行效率和生活质量，当区域拥塞节点扩散到大规模的城市路网，容易造成大规模区域路网交通拥塞。因此，研究城市交通拥塞的迁移规律，实现交通流的均衡分布，对缓解城市道路区域性甚至大规模交通拥塞具有显著意义。

目前国内外学者研究了大量的城市道路交通拥塞模型。Toan T.D.等[1]利用交通流速度和密度数据基于模糊逻辑方法量化高速公路交通控制水平。Afrin T.等[2]利用交通历史数据集对交通管控措施进行比较分析，以期提高交通控制水平。Priambodo B.等[3]使用K-M聚类方法确定相邻道路之间的空间相关性。Afrin T.等[4]考虑交通量与速度的管控措施提出基于贝叶斯网络的可能交通拥塞状态的概率估计。胡立伟等[5]基于高斯烟雨模型，开发了一种城市交通拥塞辐射新模型。

城市交通拥堵风险分析研究层见叠出，但鲜少将污染质迁移数值模拟模型运用到城市道路交通拥塞风险迁移中，诸多研究将输入模型参数及交通联通边界条件设定为定值，其输出结果与输入对应且确定唯一。对于考虑交通联通边界条件不确定性的研究更是寥寥无几。

近些年来，不确定性分析主要用在地下水污染质运移方面。Hauser等[6]将潜水含水层地质结构和水文地质参数的不确定性因素考虑到数值模拟模型中，发现两者共同作用导致地下水位的不确定性。常振波等[7]考虑污染质运移数值模拟模型中水文地质参数的不确定性对研究区遭受污染风险进行分析与预报。黄建华等[8]提出基于UAU-SIR 模型的多重预警信息下的拥堵传播机制。孙建平等[9]基于城市交通事故时空特征，提出速度差异的拥塞判别模型。韦清波等[10]考虑多因素并对城市交通拥堵指数进行分段预测。王忠宇等[11]提出基于网络变结构模型分析城市大型活动的交通运行状态和拥堵规律。

然而以往许多交通拥塞研究忽略交通联通边界的交通量及交通扩散系数对交通拥塞扩散规律的影响、未精确预报研究区域交通拥塞风险分布迁移规律以及多数研究将模型参数不确定性作为研究核心等问题，忽略了边界条件不确定性的影响。在城市交通拥塞风险迁移数值模拟过程中，模拟预报结果的正确与否和交通联通边界条件处理得是否恰当密切相关。本文提出一种新的城市道路交通拥塞风险分布迁移模型，借鉴地下水污染和交通拥塞风险在有限空间内迁移的相似性，结合城市历史交通量、速度等数据，充分考虑城市发展交通联通边界的交通量及交通扩散系数对研究区域(路段、交叉口、子区)的影响，并深入分析不同高峰小时时段交通拥塞风险分布迁移规律差异性，相比现有高德地图预测数据，模拟模型输出结果精度更高，可以更好地刻画交通拥塞风险分布迁移规律，为研究城市交通拥塞提供新参考。

1 基于替代模型的城市交通拥塞风险评价方法

1.1 研究区域概况

本文使用贵阳市某区域内的部分路网对城市外围交通边界问题进行研究。为简化研究内容，定义为一个东西长5000 m，南北宽3250 m，总体交通流向从东北侧至西南侧的不规则研究区域，交通量为均质各向同性且非均匀稳定流。根据2020年6～7月的城市交通调查数据，并结合研究区域具体情况，将研究区域划分为区域1 和区域2；区域1 主要为居住用地等，区域2 主要为学校用地、工业用地等。区域1单个节点最低交通量为1200 pcu·h-1，区域2单个节点最低交通量为1080 pcu·h-1，交通量通过交叉口等关键节点进行横纵向疏散，在垂向上由区域内的自生交通量产生，区域1多年的交通量出行系数为0.20～0.25，区域2多年的交通量出行系数为0.25～0.30，忽略部分路段路内停车泊位。各区域内交通基础设施完善，交通信号控制良好。西北侧边界τ1和东南侧边界τ3均为城市研究区域发展边界线，视为交通隔断边界；东北侧边界τ2是连接城市外围发展的重要边界，有较大的交通量且与研究区域具有较好的交通联系；西南侧边界τ4是连接城市重要卫星城镇的重要边界，西南侧主要分布大量的旅游资源等，早、晚高峰交通量较小，但与研究区域具有较好的交通联系，东北侧边界τ2和西南侧边界τ4均可视为交通联通边界。划分后研究区域的相关参数取值如表1所示。

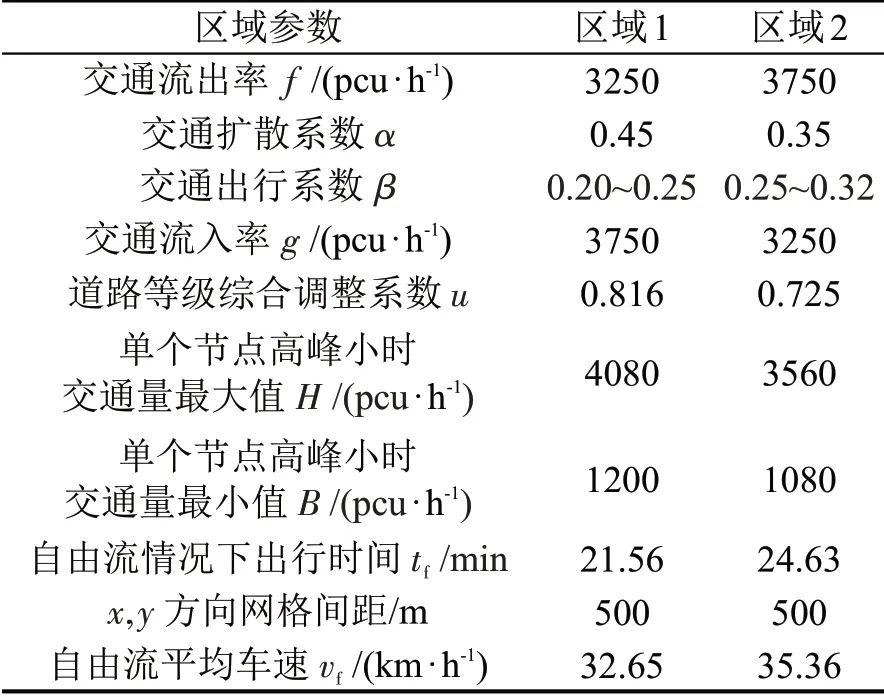
表1 路网区域参数取值Table 1 Road network area parameter value

区域1 主要为居住用地，城市交通的早、晚高峰容易致使区域1内的拥塞扩散到区域2。为预测交通联通边界高峰小时交通情况(交通量、交通扩散系数)对研究区的影响，建立交通拥塞迁移数值模拟模型，模拟时间为早、晚高峰各1.5 h，每10 min为一个时段，共计9个模拟时段。设定交通拥塞程度综合评价指数为1.45，给定交通联通边界τ2，τ4，交通隔断边界τ1，τ3分别视为零速度边界和零交通量边界。研究区主交通、次交通、非交通拥塞点位置如图1所示。

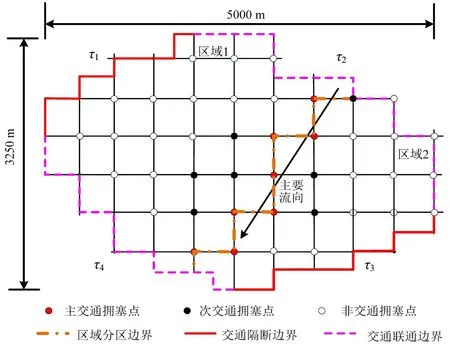
图1 城市路网基础模型Fig.1 Basic model of urban road network

研究区已知交通联通边界τ2受城市过境交通影响比较严重，城市过境交通量逐年增长，一天内交通量各有不同，导致区域2 的交通量变化明显。对交通联通边界进行预报后预测交通拥塞迁移变化。

1.2 交通联通边界预报

研究区东北侧已知交通联通边界τ2是城市外围发展的重要边界，是研究区域内交通重要产生源。分析城市2020年6～7月早、晚高峰历史数据得到，早、晚高峰时间内，高峰小时交通量最小在6648～9156 pcu·h-1，最大在6832～11098 pcu·h-1。交通扩散系数是指交通联通边界τ2上各交叉口流入研究区域交通量占各交叉口交通量的比值，无量纲。高峰小时交通扩散系数最高在0.68～0.85，最低在0.59～0.79。

高峰小时交通量最大值、最小值均随着拥塞持续时间的持续增大呈先上升后减少的趋势；交通扩散系数则呈现正态分布。城市外围高峰小时交通量及交通扩散系数变化如表2所示。

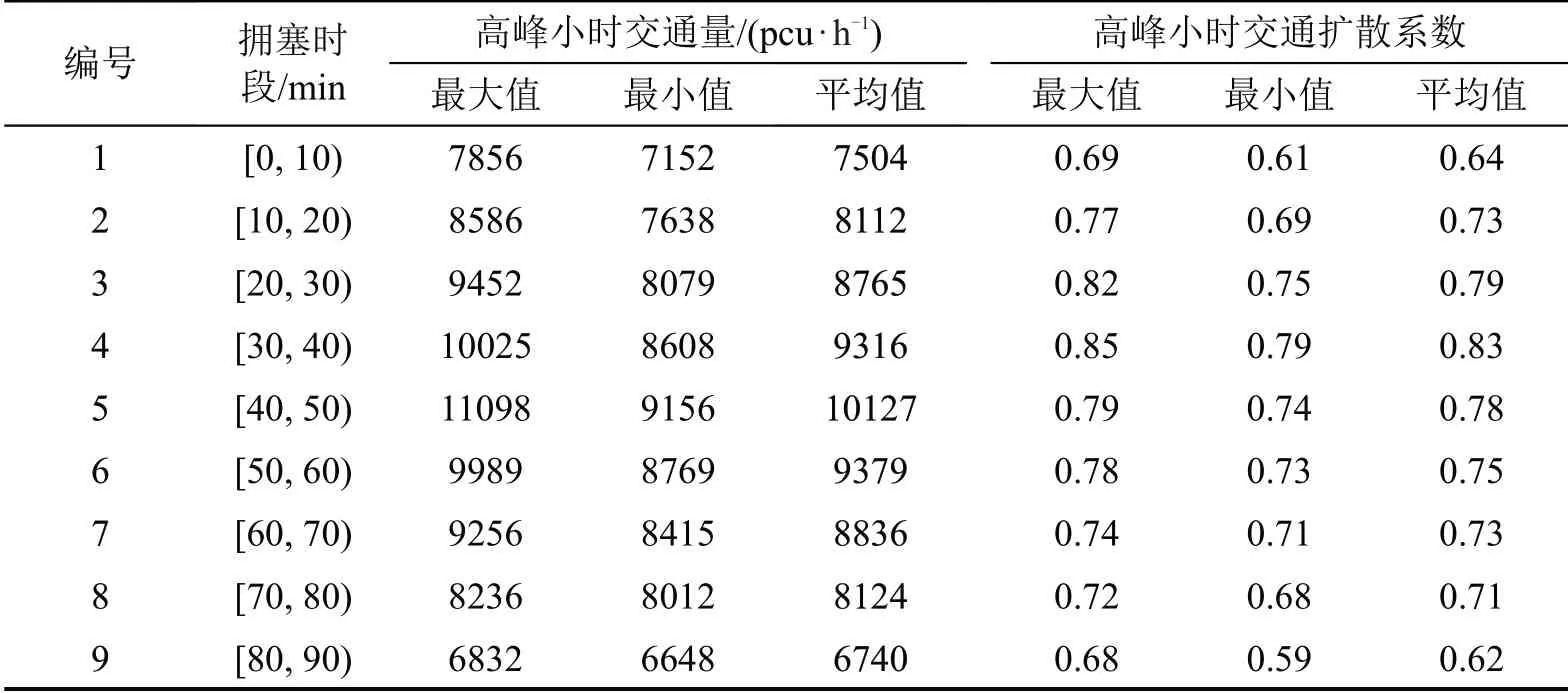
表2 城市外围高峰小时交通量及交通扩散系数取值范围Table 2 Range of peak hour traffic volume and traffic volume diffusion coefficient in periphery of city

根据数据分析得到，城市外围高峰小时交通量呈现正态分布，符合城市拥堵一般规律。交通量扩散系数变化趋势则相比交通量发展趋势具有一定的滞后性，可能是随着车辆导航系统等普及，交通联通边界τ2中一部分交通量选择绕路而行。

下面研究交通联通边界条件τ2交通量的大小和交通扩散系数对研究区域内交通拥塞迁移的影响。

1.3 建立城市交通拥塞迁移数值模拟模型

边界条件不确定性是指交通联通边界τ2的不确定性，在本文中定义边界条件是交通量和交通扩散系数，进而边界条件的不确定性是指每天交通量和交通扩散系数随时间变化取值不同。

交通量是指交通联通边界τ2上各交叉口交通量的平均值，交通扩散系数是指交通联通边界τ2上各交叉口流入研究区域交通量占各交叉口交通量的比值。

城市道路交通拥塞的范围与交叉口、路段、子区、交通量扩散系数、城市外围交通量等因素密切相关，图2为交通拥塞子区划分模型。在实际路网中，子区是城市路网的最小结构单元，交叉口和路段最少存在于两个路网子区中。图2 中，子区1 和子区2共有路段A，4个子区均包含交叉口C，交叉口被划分为C1，C2，C3，C4。将贵阳市部分路网抽象出研究区域的基础模型。

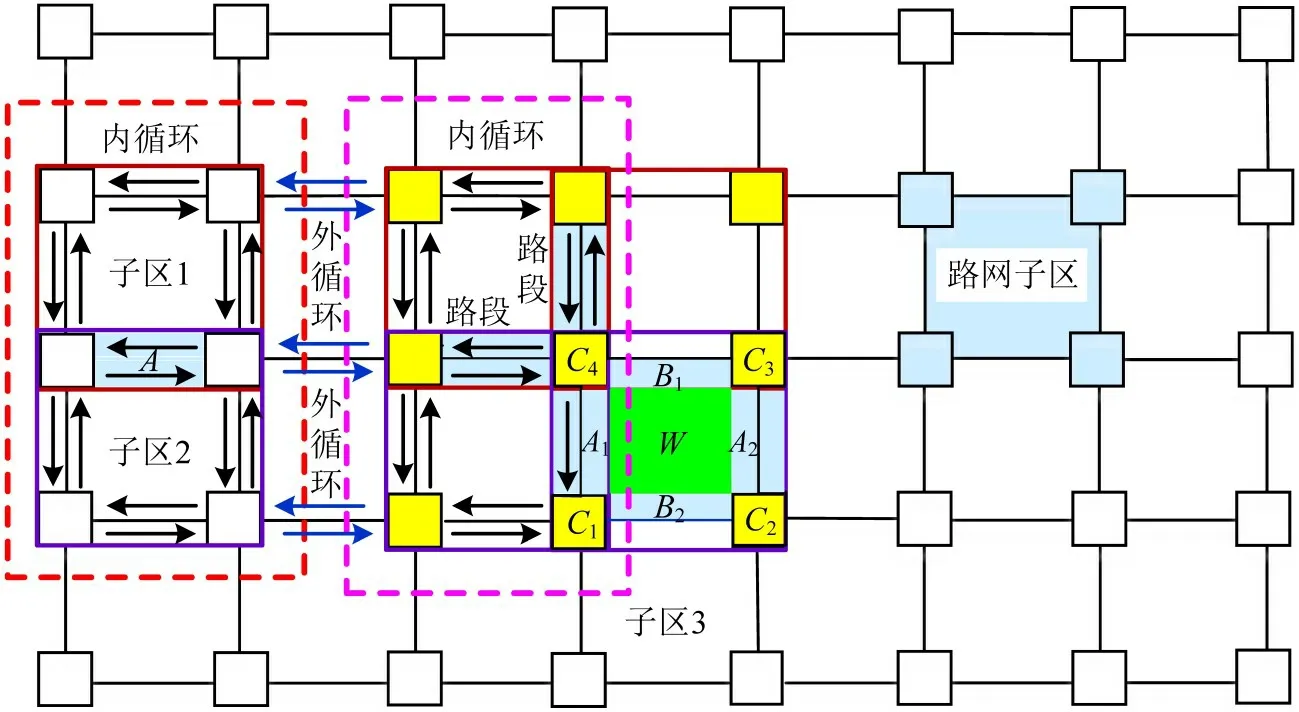
图2 路网子域划分示意图Fig.2 Schematic diagram of road network subdomain division

污染质迁移数值模拟模型经常被用来研究区域地下水污染质迁移规律。城市道路交通拥塞风险迁移与污染物在地下水中的传播扩散在理论上具有相似性，交通拥塞在城市区域路网系统中的风险迁移过程类似于污染物的迁移过程，污染水的迁移受到地下水开采、降水量、污水泄漏量、污染物释放强度等，既有内部因素，又有外部因素。同样，城市交通拥塞受到外部因素和内部因素，具有自适应规律。

同样地，城市道路交通拥塞风险迁移模型与污染物迁移数值模拟模型有相似的物理意义，对迁移数值模型进行抽象。

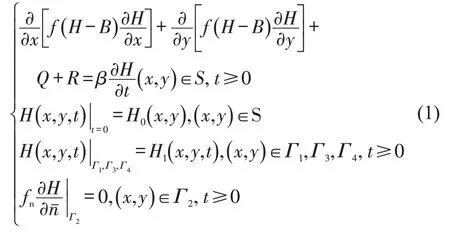
式中：S为研究区域范围；f为交通流出率(pcu·h-1)；H为单个节点高峰小时交通量最大值(pcu·h-1)；B为单个节点高峰小时交通量最小值(pcu·h-1)；Q为区域W能容纳的交通量(pcu·h-1)；R为外围交通进入研究区域交通量(pcu·h-1)；β为交通出行系数，无量纲；Γ2为变交通量和变交通扩散系数边界；Γ1，Γ3，Γ4为零速度和零交通量边界；fn为边界法向量上的交通流出率(pcu·h-1)；nˉ为子区的平均交通量(pcu)。

城市交通拥塞随交通量迁移，在交通量数值模型基础上，建立交通量交通拥塞数值模拟模型为

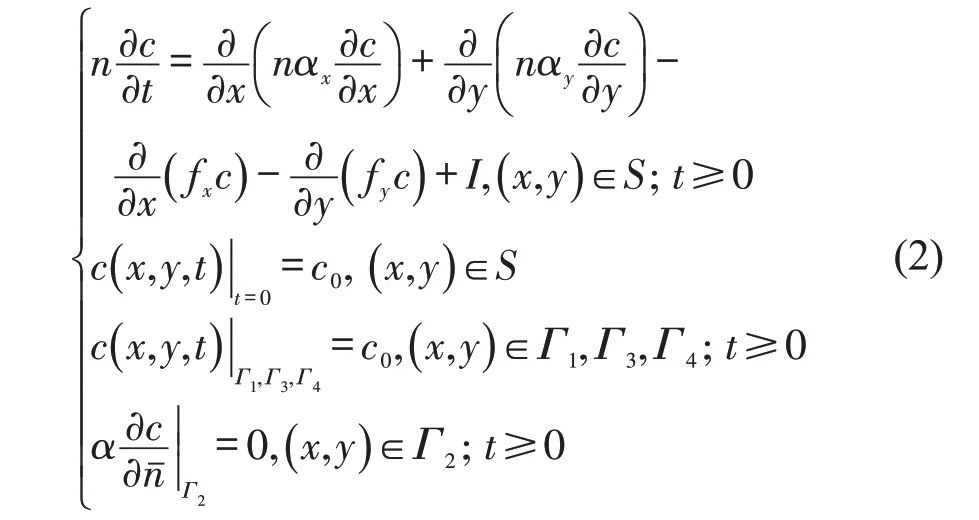
式中：n为子区的总交通量(pcu)；c0为初始设定交通拥塞综合评价指数；α为交通扩散系数，是一个量纲为1 的量；t为交通拥塞点扩散时间；x，y分别为距离交通拥塞点的横向、水平方向距离；αx，αy分别为交通扩散系数在x、y方向的分量(m2·d-1)；fx，fy分别为交通流出率f在x、y方向上的分量(pcu·h-1)；I为单位时间和面积内交通量的增减量(pcu·h-1·m-2)；c(x,y,t)为城市区域道路网络系统受交通拥塞影响的程度，是一个量纲为1的量。

本文采用交通拥塞综合评价指数表征城市道路交通拥塞程度，即

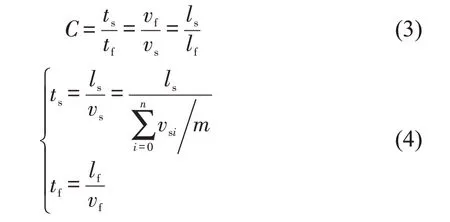
式中：C为交通拥塞综合评价指数；ts为实际出行时间；tf为自由流情况下出行时间；vs为车流的实际行程速度；vf为车辆自由流车速；vsi为第i辆车的平均行驶速度；ls为道路的实际长度；lf为道路拥塞的长度；m为路段中的车辆数。

本文将城市路网交通拥塞等级划分为“畅通”“拥塞”两大类，将“畅通”划分为2 个等级，“拥塞”划分为3个等级，具体如表3所示。

表3 城市路网交通拥塞等级划分Table 3 Classification of traffic congestion levels in urban road networks

1.4 建立替代模型

本文运用一种广泛应用于地质领域的基于最小估计方差的无偏估计预测方法建立替代模型。利用MATLAB 软件进行编程构建替代模型，输入为通过交通联通边界的高峰小时各时段的交通量、交通扩散系数的取值，输出为模型在交通量、交通扩散系数不同取值情况下运行的各高峰小时时段的交通拥塞综合评价指数。模型可以实现快速调用程序，大幅减少工作量。

利用Monte Carlo 模拟1000 组输入输出数据，通过拉丁超立方抽样方法(LHS)对交通联通边界τ2各高峰小时时段的交通量、交通扩散系数进行随机抽样，分别抽样850 组(训练样本)和150 组(检验样本)，并将抽样参数分别输入到城市交通拥塞迁移数值模拟模型中，检验建立的替代模型精度，模型计算和模型输出相对误差均未超过0.01，建立的替代模型精度很高。最后利用Monte Carlo 方法对1000 组响应输入输出统计实验进行交通联通边界分析，并对交通拥塞综合评价指数进行统计，得到交通拥塞综合评价指数均值，方差等估计量和概率分布情况。替代模型精度检验情况如图3所示。交通联通边界预报-城市交通拥塞迁移数值模拟模型-替代模型三者之间的关系如图4所示。

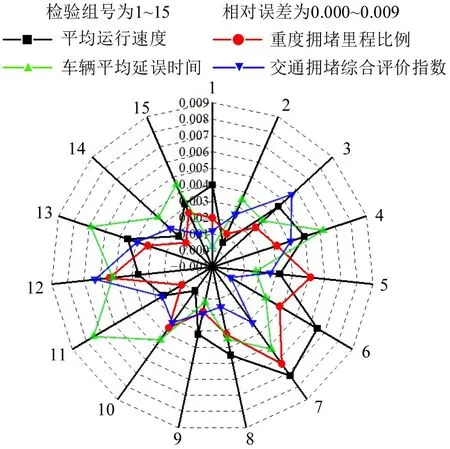
图3 拟合精度检验Fig.3 Fit precision test

图4 交通联通边界预报-城市交通拥塞迁移数值模拟模型-替代模型三者之间的关系Fig.4 Relationship between traffic connectivity boundary forecast-numerical simulation model of urban traffic congestion migration-alternative model

2 结果与讨论

本文主要对研究区域交通联通边界τ2高峰小时9个时段(每个时段10 min)变交通量和交通扩散系数进行统计分析。运用替代模型输出研究区域内高峰小时时段内的交通拥塞综合评价指数值，利用实测的数据对研究区域内的交通拥塞综合评价指数进行估计，并对研究区域交通拥塞风险进行统计分析。

2.1 对比分析

讨论交通联通边界τ2的交通量和交通扩散系数对交通拥塞风险迁移的影响。运用实测数据进行计算，将交通联通边界τ2取定值计算交通拥塞综合评价指数(数值模拟模型中各个时段中交通量保持不变或者交通扩散系数保持不变)并进行对比，结果如表4所示。对比发现，两种情形下研究区域内的交通拥塞综合评价指数值相差很大，说明交通联通边界τ2的不确定性对城市交通拥塞的迁移有较大影响。

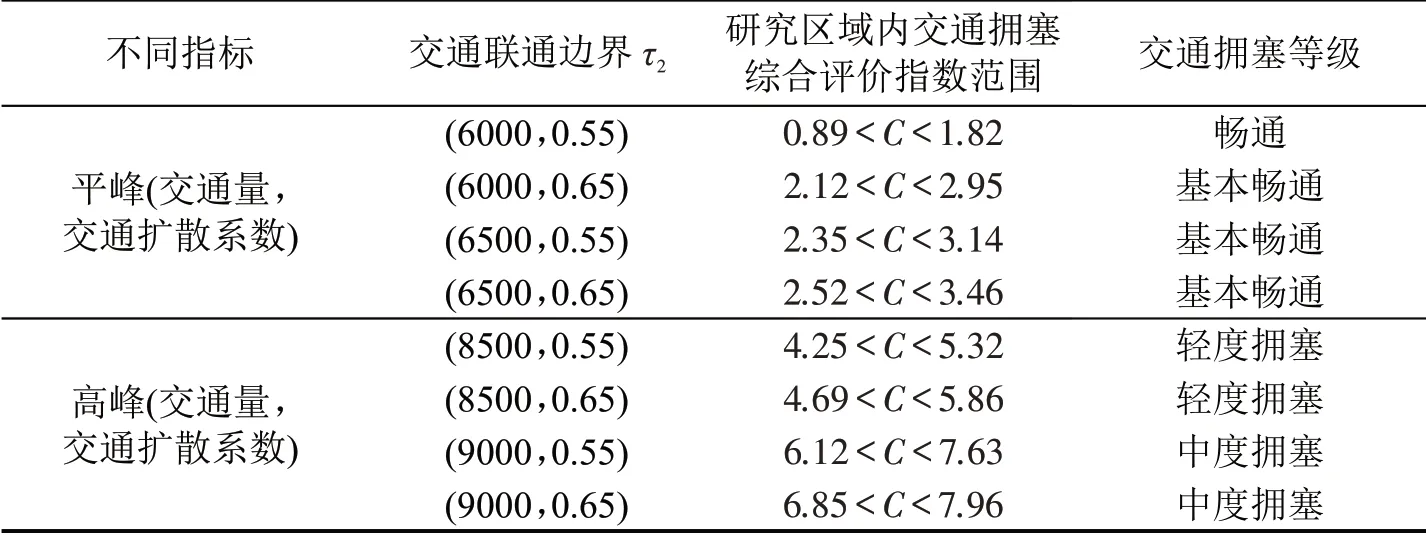
表4 研究区域交通拥塞综合评价指数对比Table 4 Comparison of comprehensive evaluation index of traffic congestion in study area

在不考虑交通联通边界τ2不确定性(平峰时间下的交通量和交通量扩散系数)的情况下，平峰1.5 h内交通拥塞综合评价指数很低，几乎未发生拥塞情况。在考虑交通联通边界τ2不确定性的情况下，研究区域内高峰小时各时段的交通拥塞综合评价指数明显增大，造成这种结果的原因是城市外围发展交通联通边界τ2在高峰时间及出行方式选择的耦合作用下使得区域内交通量变大，道路供给及信号控制配时不合理等，使得在异质同等时间段内研究区域更为拥塞，考虑交通联通边界τ2具有重要意义。研究区域内交通拥塞综合评价指数范围最大、最小值对比箱型图如图5所示。

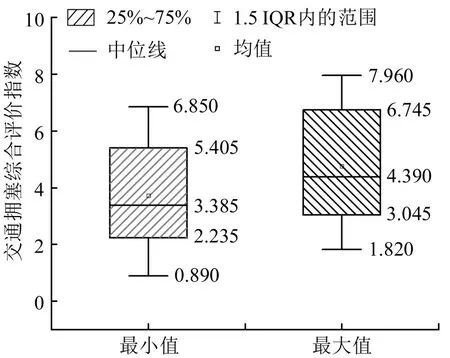
图5 研究区域交通拥塞综合评价指数范围最大、最小值对比箱型图Fig.5 Comparison of maximum and minimum range of comprehensive evaluation index of traffic congestion in study area

2.2 研究区域交通拥塞综合评价指数分析

该模型在原来的基础上考虑了交通联通边界τ2的交通状况(交通量、交通扩散系数)对研究区域交通拥塞范围的影响，为验证观点的有效性，将考虑交通联通边界τ2后的模型输出与未考虑交通联通边界τ2的研究区域路网真实情况进行对比分析，如图6所示。交通联通边界的交通量、交通扩散系数的不同，势必会影响研究区域内交通拥塞风险分布迁移，研究区域交通拥塞综合评价指数对比如表5所示，因此通过控制单一变量，对研究区域内交通拥塞风险分布迁移规律进行验证和分析，如图7所示。

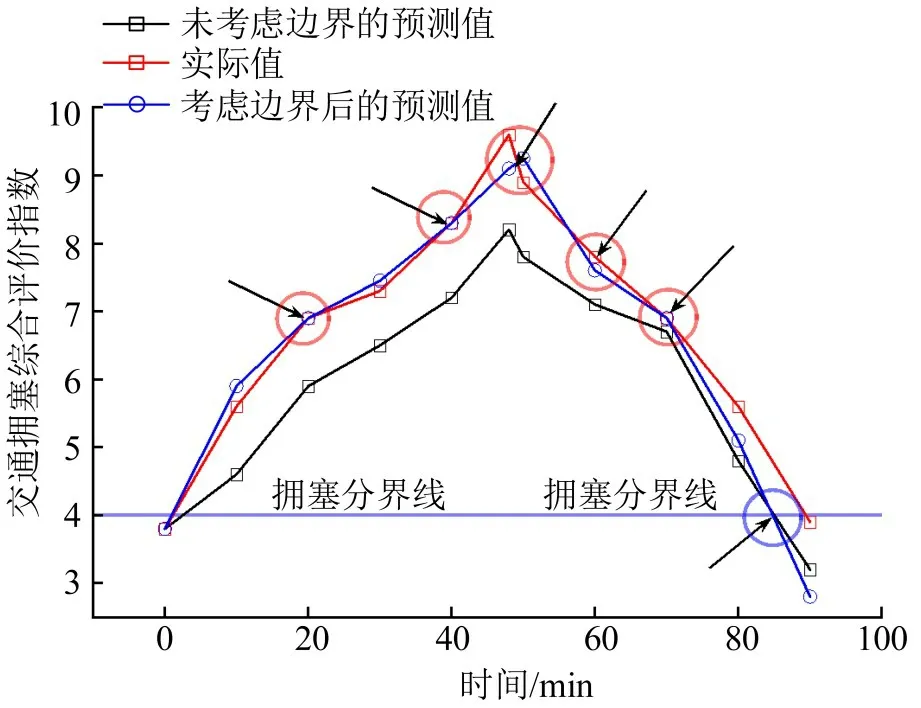
图6 考虑交通联通边界τ2 与否模型预测结果和实际情况对比分析Fig.6 Comparative analysis of prediction results of original model and model after considering transportation boundary τ2

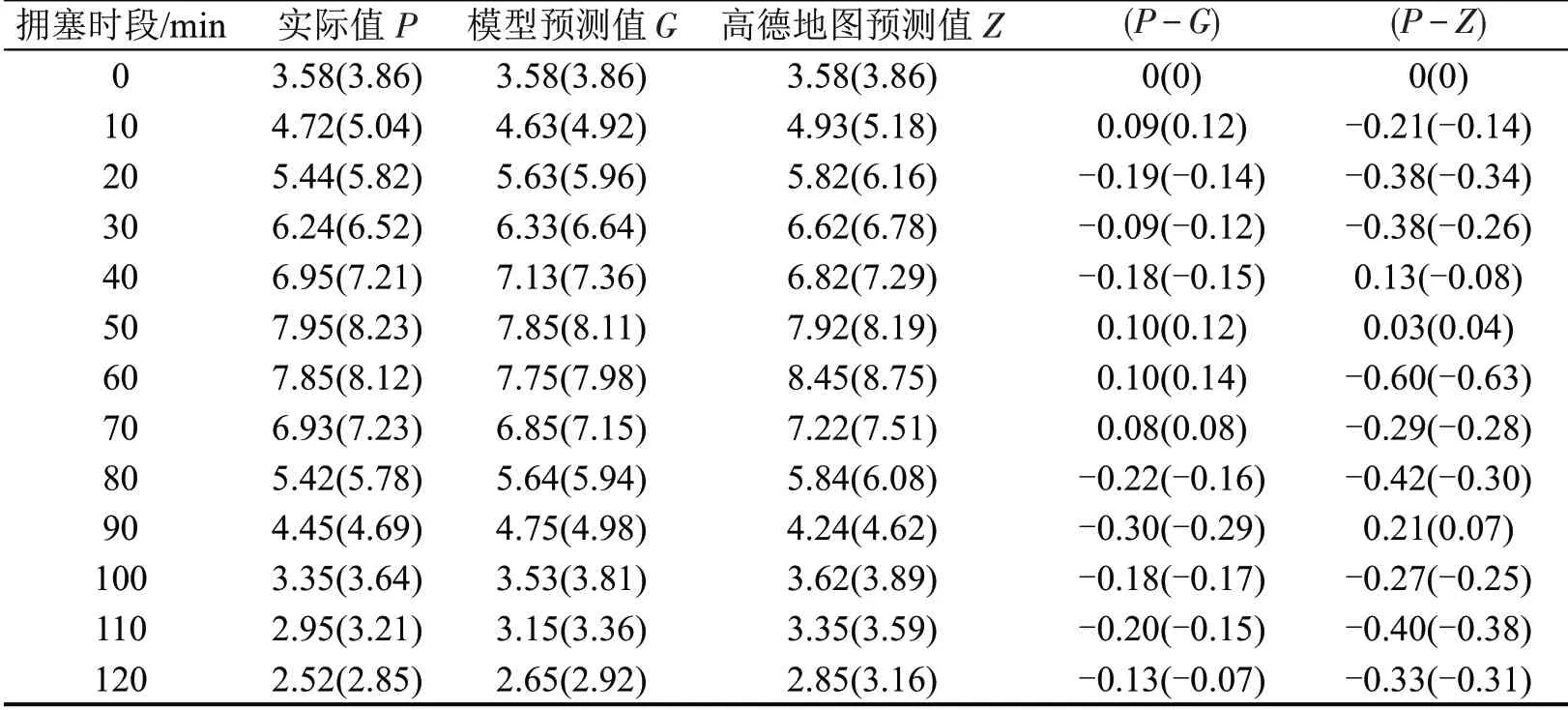
表5 研究区域内交通量相同，交通扩散系数为0.75(0.85)的交通拥塞综合评价指数对比Table 5 Comparison of comprehensive evaluation indexes of traffic congestion with same traffic volume in study area and a traffic diffusion coefficient of 0.75(0.85)

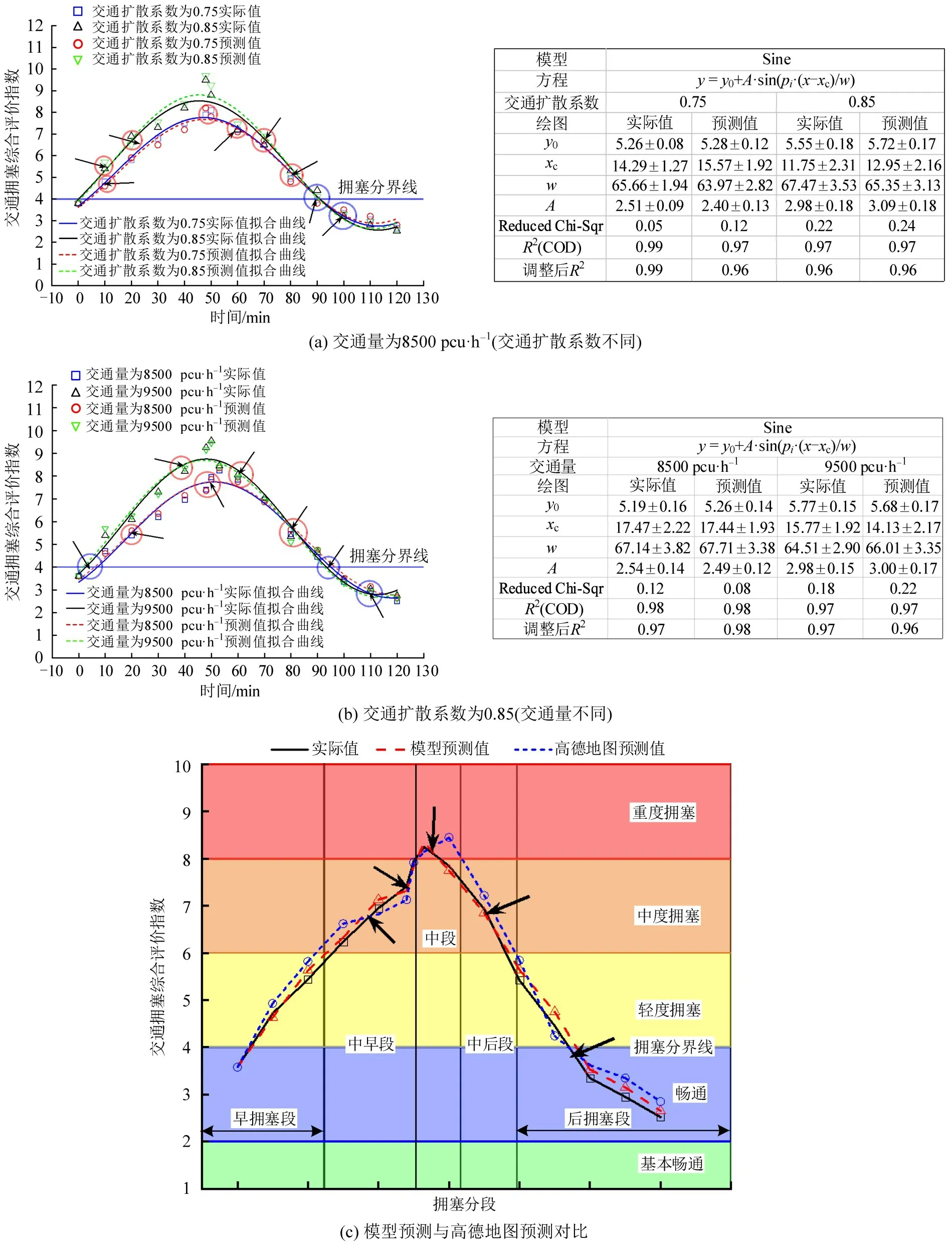
图7 不同情况下交通拥塞综合评价指数预测Fig.7 Comprehensive evaluation index prediction of traffic congestion under different conditions

通过对历史数据进行统计分析，当交通量相对恒定，交通扩散系数为0.75 时，研究区域的整体拥塞情况可以演化城市交通的重要拥塞情况；为了更好地描述交通扩散系数单一变量对城市交通拥塞的影响，故取交通扩散系数的85分位进行刻画。

图7(a)为交通联通边界τ2在交通量相同，交通扩散系数不同的交通拥塞综合评价指数预测结果，交通扩散系数为0.75时，模型预测交通综合评价指数范围在2.80～8.20，实际值为2.65～8.10，预测交通拥塞消散时间为52 min。交通扩散系数为0.85时，模型预测交通综合评价指数范围在2.86～9.70，实际值为2.52～9.50，预测交通拥塞消散时间为48 min。在两种交通扩散系数标定下预测结果均与实际情况相差较小，拟合度较高。

图7(b)为交通联通边界τ2在交通扩散系数相同，交通量不同情况下的交通拥塞综合评价指数预测结果，交通量为8500 pcu·h-1时，模型预测交通综合评价指数范围在2.65～8.35，实际值为2.50～8.25，预测交通拥塞消散时间为53 min。交通量为9500 pcu·h-1时，模型预测交通综合评价指数范围在2.62～9.45，实际值为2.75～9.55，预测交通拥塞消散时间为52 min。在两种交通量标定下预测结果均与实际情况相差较小，拟合度较高。

图7(c)为交通联通边界τ2引起的交通拥塞风险分布迁移规律，整体来看交通拥塞的风险分布迁移模型预测结果，在49.35 min时，预测的交通拥塞综合评价指数最大为7.88，实际值为8.05，与实际值误差仅为2.11%，高德地图预测结果为8.52，误差达到5.84%。模型预测交通拥塞风险迁移变化下降时间为54 min，实际值为55 min。高德地图预测风险迁移变化下降时间为59 min，可见模预测结果较高德地图要好，总体模拟模型精度较高。研究区域交通拥塞综合评价指数范围最大、最小值对比箱型图如图8所示。

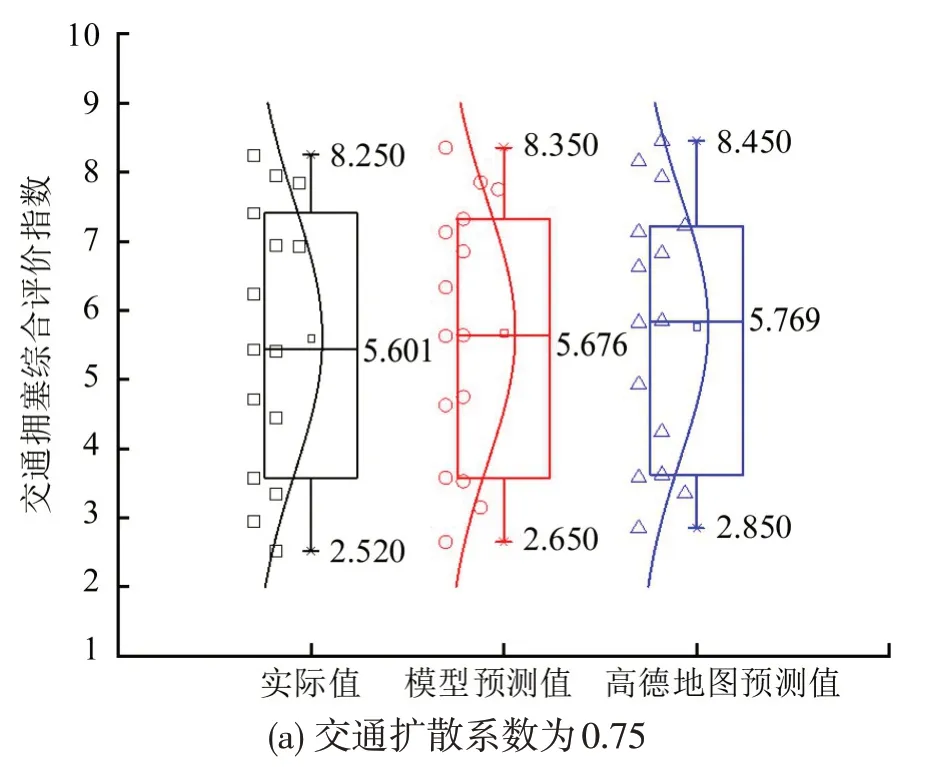
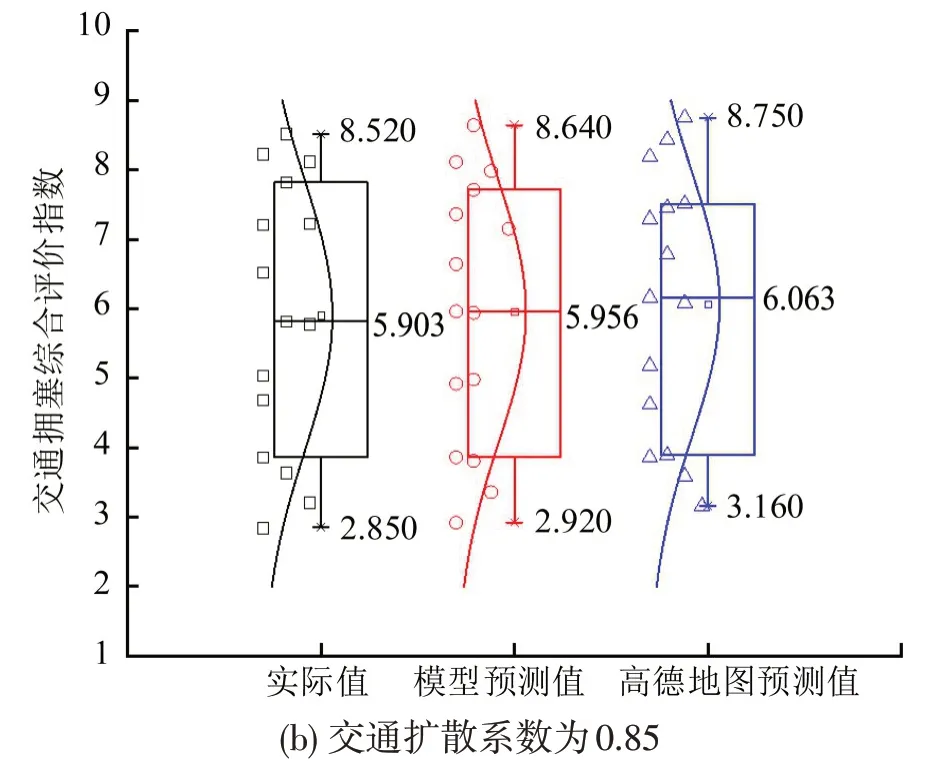
图8 研究区域交通拥塞综合评价指数范围最大、最小值对比箱型图Fig.8 Comparison of maximum and minimum range of comprehensive evaluation index of traffic congestion in study area

3 研究区域交通拥塞迁移比较应用研究

除了对交通联通边界τ2的交通量及交通扩散系数进行对比，也对研究区域内早、中早、中、中后、后时段末刻的交通拥塞迁移情况进行了对比。图9为早期交通拥塞风险分布实际、模型预测、高德地图预测迁移图，高德地图预测相较于模型预测精度较低，模型预测更接近于实际情况。

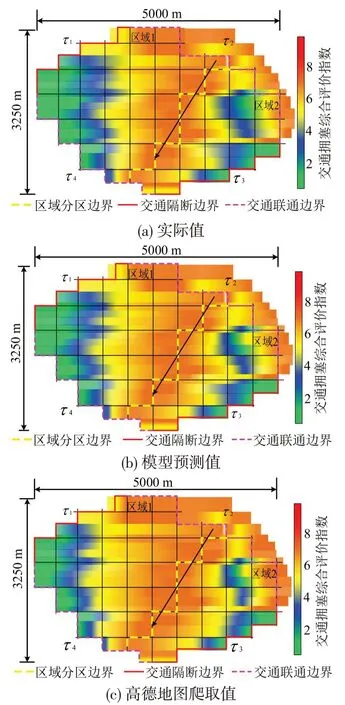
图9 研究区域高峰时间早期拥塞分布情况Fig.9 Early peak hour congestion distribution in study area

图10 为中早交通拥塞风险分布实际、模型预测、高德地图预测迁移图。以此类推，同样得到中拥塞段、中后拥塞段、后拥塞段的交通拥塞风险分布实际、模型预测、高德地图预测迁移图，分别如图11～图13所示。

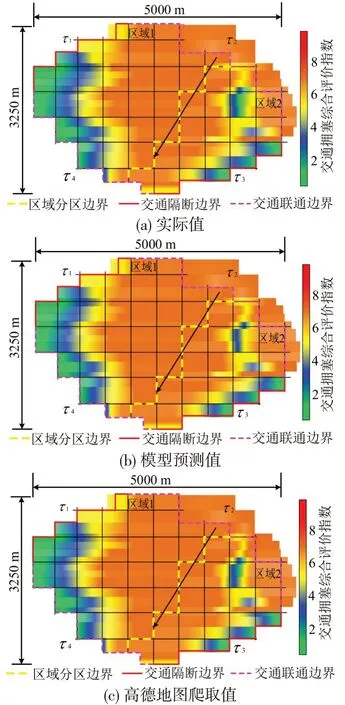
图10 研究区域高峰时间中早期拥塞分布情况Fig.10 Early congestion distribution during peak hours in study area

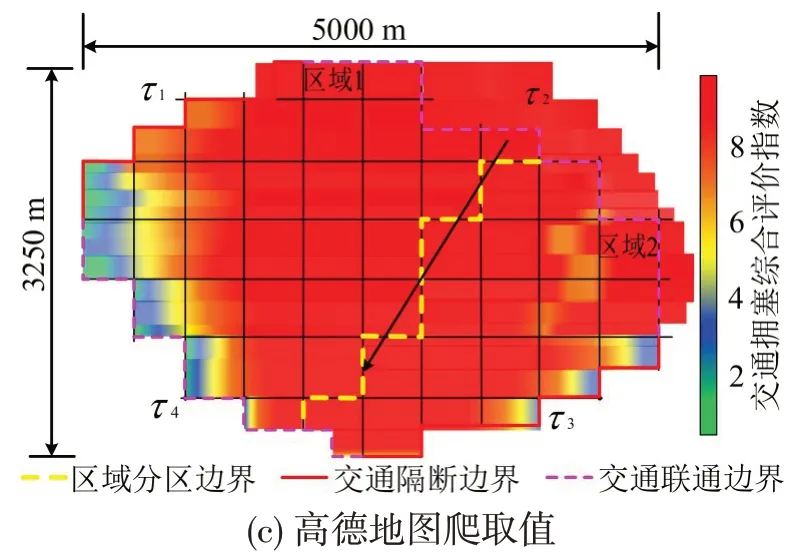
图11 研究区域高峰时间中期拥塞分布情况Fig.11 Mid-peak hour congestion distribution in study area

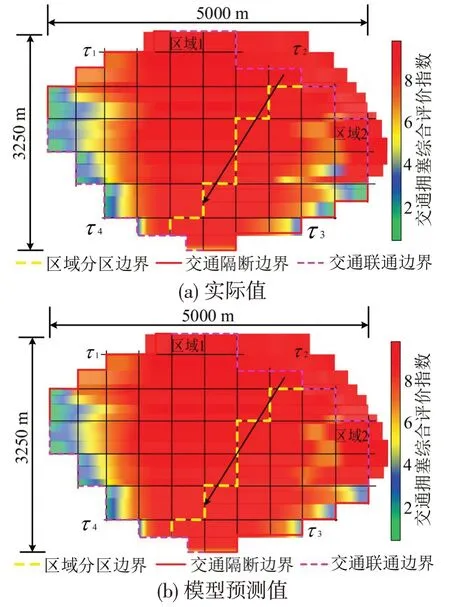
图12 研究区域高峰时间中后期拥塞分布情况Fig.12 Study area mid to late peak hour congestion distribution

由图9～图13 可知，对交通联通边界τ2进行预测预报，并考虑交通联通边界τ2的交通状况(交通量、交通扩散系数)对城市研究区域内交通拥塞风险迁移分布情况影响很大，5 种情况下的交通拥塞风险分布晕覆盖情况有很大差距。图11～图13中，因为交通量、交通扩散系数的逐渐减少，交通拥塞风险迁移较慢，交通拥塞风险分布范围更小。

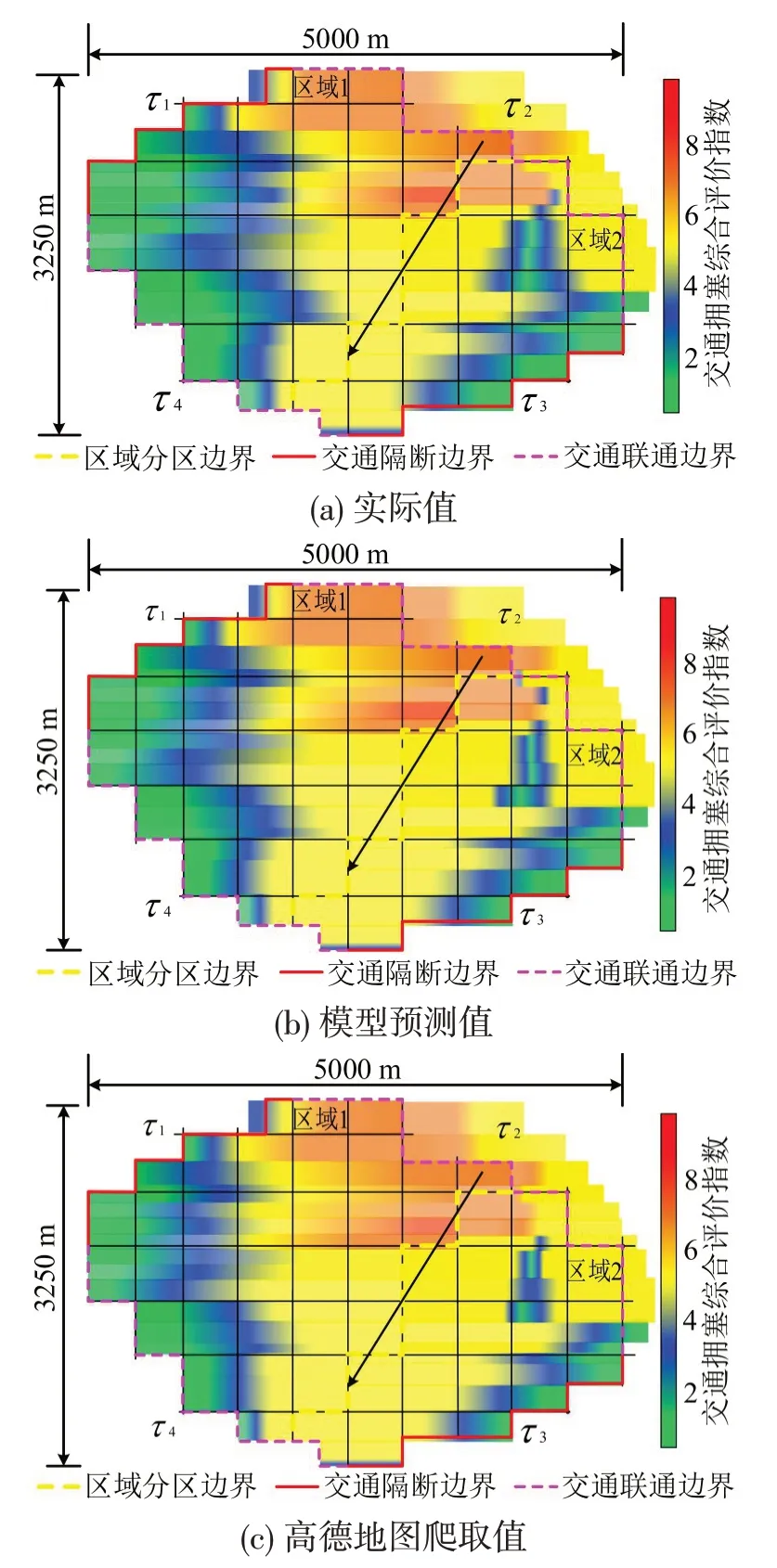
图13 研究区域高峰时间后期拥塞分布情况Fig.13 Distribution of late peak hour congestion in study area

4 结论

(1)通过替代模型模拟城市交通拥塞迁移数值模型输入输出响应关系，可有效减少调用数值模拟模型的工作量，且替代模型精度较高；通过对比分析城市高峰时间“早期-中早期-中期-中后期-后期”交通拥塞演变规律，结果表明，建立的城市交通拥塞数值模拟模型比高德地图预测精度更高。

(2)运用Monte Carlo 对输出的交通拥塞综合评价指数进行统计分析发现，不同高峰小时时段交通拥塞风险分布差异较大，可以较好地演示城市交通拥塞风险的迁移规律。