机翼‑机身柔顺对接装配及接触力分析方法
罗 群,王 青,刘之珩,刘博峰,张 强
(1.中航西安飞机工业集团股份有限公司,西安 710089;2.浙江大学浙江省先进制造技术重点实验室,杭州 310027)
飞机装配是飞机制造过程中的重要组成部分,涉及学科领域广泛、难度较大,是一项综合性制造技术[1-2]。其中,机翼装配精度要求高、配合件昂贵、装配难度大,精度要求在0.05 mm 以内。传统机翼机身对接装配使用专用型架配合人工辅助的方式进行装配[3-4],由于人工操作误差、型架制造误差,机翼位姿精度难以保证,而机翼连接结构间隙狭小,装配过程中产品易发生变形、碰撞和磨损。为了提高装配质量,目前主要有两种方式:(1)使用由数字测量系统[5]、数字定位装置、控制系统组成的数字化调姿定位系统来提高调姿定位精度[6-7];(2)使用柔顺对接技术来平滑对接过程中的接触力[8-9]。但上述方式仍难以保证对接装配的顺利进行。原因有:(1)连接结构装配精度要求高且要尽量避免发生碰撞、磨损等现象,目前调姿定位系统尚难以做到;(2)由于装配部件质量较大,安装到夹紧设备上时会出现部件与设备在位姿上的偏差,这种偏差可能会对后续的对接过程产生不利影响;(3)柔顺对接机构虽然一定程度上可以平滑、降低对接过程中的接触力,但由于没有科学的接触力计算模型,对接过程中仍存在接触力过大的可能。为了应对上述问题,本文建立了接触力计算预测模型,可以根据装配参数,通过测量部件在对接开始前的位姿偏差,提前计算、预测出装配过程中装配件受力最大值。如超过阈值则终止对接,避免了对接过程中因接触力过大而导致装配件的损伤。机翼常用的连接方式有轴孔式连接结构[10]和叉耳式连接结构[11],本文以叉耳式连接结构为研究对象。
1 机翼装配数字化调姿及柔顺对接机构
机翼结构形式多种多样,如边条翼、后掠机翼、前掠翼和三角翼等,翼身对接形式也不尽相同,如叉耳、轴孔和齿垫等形式。为降低制造成本、提高装配效率,需要设计一种面向机翼对接装配的柔性工装,通过快速重构满足不同机型、不同连接形式的对接装配要求。
基于上述需求,浙江大学飞机数字化装配课题组设计了一种结合数字化调姿定位技术与柔顺对接技术的机翼数字化调姿对接系统[10,12]。该系统既可以满足机翼在各种小间隙连接形式中的低应力无损装配,又实现了调姿对接系统与装配部件“一对多”的模式,不再局限于特定机型、特定对接形式,充分体现了数字化、柔性化的装配理念。
1.1 机翼数控定位系统
机翼数字化调姿及柔顺对接系统一般由机翼数控定位系统完成机翼部件的初始定位,将装配件的相对偏差控制在一定范围内,然后在对接过程中,通过柔顺对接机构补偿该部分偏差,实现低应力无损装配。机翼数控定位系统主要由底座和调姿定位器组成,如图1 所示。
1.1.1 数控定位系统底座
底座作为安装数控定位器等设备的平台,需要有较强的承重能力与稳定性。底座主要由整体平台和支撑脚组成。底座长4 200 mm,宽2 900 mm,高850 mm,平台四角布置有4 处平台吊点。框架底部布置有升降支撑脚,升降行程450 mm,在机翼对接时使平台下降,可降低底座重心,提高设备稳定性。

图1 机翼数控定位系统Fig.1 Digital positioning system of wing-fuselage
1.1.2 机翼调姿数控定位器
机翼调姿数控定位器是一种可以实现X、Y、Z这3 个坐标方向数控移动的模块化单元,且X、Y、Z轴均采用全闭环控制。每个机翼调姿定位系统含有4 个三坐标数控定位器,共有12 个相互独立的驱动轴。通过对各个定位器的协同控制,可以实现所支撑产品的六自由度高精度调姿,并确保不会对产品造成撕裂、挤压等损伤。每台调姿数控定位器主要由底座、定位轴、各定位轴托板、立柱、定位器电控柜及球头入位装置等组成,如图2 所示。

图2 数控定位器Fig.2 Numerical localizer
1.2 柔顺对接机构
如图3 所示,柔顺对接机构主要由五自由度柔顺机构和对接进给机构组成。柔顺对接机构具备一定误差适应性。
1.2.1 柔顺机构
如图4(a)所示,五自由度柔顺机构主要由上底板、下底板、导向柱、导向套、转动滑轨、直线滑轨、拉伸弹簧和碟簧等组成。其中,直线滑轨固定在底板上,用于实现下底板的直线运动;转动滑轨固定在下底板,用于实现上底板的回转运动;上底板通过球铰的方式与托架过渡件进行连接;竖向拉伸弹簧连接于固定底板和托架过渡件之间;斜向拉伸弹簧连接于固定底板和上底板之间;碟簧位于导向套内,连接于上底板和托架过渡件之间。

图3 柔顺对接机构Fig.3 Compliant docking mechanism
图4(b)是柔顺机构的机构运动简图,图中坐标系以回转中心为原点O,直线导轨方向为X轴,纵向为Z轴。图中,R 代表旋转副、P 代表平移副、S 代表球铰副。其中P1即为直线滑轨,连接固定底板和下底板;R1即为转动滑轨,连接下底板和上底板;上底板和托架过渡件之间通过4 个RPS 运动链相连。整体机构而言,固定底板通过P1、R1、4-RPS运动链连接到末端平台即托架过渡件。整个运动机构由12 个构件、5 个旋转副、5 个平移副、4 个球铰副组成。

图4 柔顺机构Fig.4 Compliant mechanism
4-RPS 机构存在过约束问题,采用修正的Kutzbach-Grubler[13]算法可以计算整个机构的自由度

式中:n表示构件数,为12;g表示运动副数,为14;fi表示运动副的相对自由度,旋转副和移动副为1,球铰副为3;μ表示过约束数,为1;代入计算后得到柔顺机构的自由度为M=5。
柔顺机构在各个自由度上的弹性刚度为

式中:[KX,KZ,Kα,Kβ,Kγ]分别为整个机构即托架过渡件相对于固定底板在X、Z方向上的平移刚度和α、β、γ方向上的旋转刚度;K1、K2、K3分别为每组竖向拉伸弹簧、斜向拉伸弹簧、碟簧的劲度系数;lX、lY分别为两组竖向拉伸弹簧几何中心沿X、Y方向上的距离;R、r分别为斜向拉伸弹簧、碟簧距离上底板回转中心之间的距离;θ为斜向拉伸弹簧与X轴的夹角,大小为45°。
1.2.2 柔顺机构进给轴
为了装配能够顺利对接,在柔顺平台中加入了对接进给轴,用于推动部件完成对接。通过电机驱动蜗轮蜗杆及滚珠丝杆带动对接进给组件运动,如图5 所示。

图5 对接进给机构Fig.5 Docking feed mechanism
为了避免对接过程中装配件因受力过大而损坏,需要对进给力进行监测,规定对接过程中进给力不能超过设定阈值(与材料特性与装配安全系数有关,不在本文讨论范围之内)。为了获得进给力,安装了扭矩传感器。通过扭矩传感器的读数T,可由式(3)算出对接过程中的进给力FZ。

式中:η为滚珠丝杆传动效率;Ph为导程,均可由所选滚珠丝杆型号获得相应参数;T0为接触前的扭矩;T为当前接触状况下的扭矩。
柔顺对接机构虽然可以一定程度上平滑翼身对接过程中的接触力,但由于缺乏科学的接触力计算模型,对接过程中仍存在部件因接触力过大而导致损伤的可能。因此,需要建立一套连接结构在柔顺对接过程中的接触力模型。通过该模型可以根据对接开始前的位姿误差计算预测对接过程中的接触力大小,以接触力大小为指标对位姿误差进行限定。此外,还可以根据该模型与调姿数控定位系统的位姿精度,指导柔顺平台的设计。
2 叉耳式连接结构柔顺对接过程接触力建模
在叉耳式连接结构对接中,由于连接结构相互干涉、挤压、碰撞会产生接触力,接触力主要包括两类:接触区域的受力、接触区域附近产生的应力。接触力过大可能导致叉耳式连接结构在对接过程中出现擦伤、磨损甚至变形,因此接触力水平是衡量对接质量的重要指标。
2.1 对接模型简化
典型的机翼叉耳装配结构如图6 所示。机身位置固定,机翼通过夹紧装置固定在柔顺进给机构上,通过电机控制柔顺进给机构完成装配。机翼的叉耳装配需要满足精密的配合要求,同时不能对配合面造成刮擦。

图6 机翼叉耳装配示意图Fig.6 Assembly schematic of wing fork-lug
机翼的装配中共有6 组叉耳对接结构。对接装配过程中以其中一组叉耳为基准进行调姿、匹配和对接,其他的叉耳结构均为间隙较大的间隙配合,这样可以避免在对接过程中其余结构先接触,保证第1 组叉耳的顺利对接装配。对接完成后单双叉耳之间的配合尺寸为33F8/h7(双面配合间隙为0.025~0.089 mm)。这种装配精度不能简单地通过数字装配的方式来进行,需要使用柔性装配技术来完成。同时,应尽可能降低配合面的受力、避免配合面的损伤。
在翼身对接开始前,叉耳式连接结构的位姿偏差可以用(X0,Y0,Z0,α0,β0,γ0)表示。其中,X0、Y0如图7(a)所示,由于Z方向为对接方向,所以Z方向的平移误差可以不记入考虑。其中Y方向的平移误差并不会影响对接过程中关键结构受力,建模过程中可以忽略。因此,平移误差主要考虑X0。

图7 叉耳式连接结构的位姿偏差Fig.7 Pose errors of fork-lug connection structure
如图7(b)所示,α0由于不会影响对接过程中关键结构的受力,在建模过程中可以忽略。结合叉耳式结构对接的结构特点,γ0在对接过程中并不会在柔顺导向的作用下发生变化,暂不考虑γ0。因此转动误差主要考虑β0。综上所述,叉耳式结构柔顺对接过程可以转化为YOZ平面内的二维模型。如图8 所示。

图8 叉耳式连接结构柔顺对接模型Fig.8 Compliant docking model of fork-lug connection structure
2.2 接触力分段建模
为了将机翼叉耳柔顺装配问题简化为数学模型,应当先做出如下假设[14-16]:
(1)由于在对接过程中相对偏差较小,对接过程中不考虑配合件的形变。
(2)柔顺机构的转向刚度Kθ和侧向刚度KX相互独立且保持恒定。
(3)由于机翼部件的刚度大于柔顺机构的刚度,同时对接过程中的位移形变很小,所以假设所有的位移形变均发生于柔顺机构的弹性形变。
(4)由于进给速度较为缓慢,整个对接过程可以假设为准静态状态。
(5)主要关注对接过程中配合件之间的受力情况,并不研究对接过程中对接轴的驱动能力,所以可以忽略重力的影响。
按照上述假设,机翼的叉耳装配过程可以简化为一个二维模型。如同前文所述,本文假设以托架为基准进行调姿,因此进给方向偏差几乎为零。偏差主要出现在机翼与机构的相对位姿:侧向偏差X和角度偏差θ。
其中,侧向偏差X以向左为正,角度偏差θ以绕夹紧机构逆时针旋转为正。X0为初始侧向偏差,θ0为初始角度偏差,这两个量在机翼固定在柔顺进给机构后可以测量得到。根据不同情况下侧向偏差X0和角度偏差θ0的正负,如图9 所示共有4种情况。

图9 初始X0和θ0 的4 种情况Fig.9 Four cases of X0 and θ0
装配过程中的主要参数如图10。其中,L为耳片的长度,w为倒角高度,α为倒角角度,h和H分别为耳片厚度和双叉耳的间距,c为双叉耳厚度,D为叉耳直径,P为双叉耳长度,FX为柔顺进给机构的侧向力,FZ为进给力,M为弯矩。

图10 主要参数及其示意图Fig.10 Main parameters and schematics
如图11 所示,整个装配过程分为4 个阶段:(1)接近倒角,(2)通过倒角,(3)单侧面接触,(4)双侧面接触。由于阶段(1)不发生接触,没有对接力出现,故从阶段(2)开始进行分析。

图11 装配过程的4 个阶段Fig.11 Four stages of assembly process
2.2.1 通过倒角阶段
在不考虑进给力等其他因素的情况下,装配成功进行的要求即是:耳片与叉耳初次接触时,耳片外沿至少应落在倒角外沿之内。这一关系的数学表达式为



图12 初始接触状态Fig.12 Initial contact state
如图13 所示,此阶段耳片与倒角相接触。本文假设初始状态下侧向偏差X0和角度偏差θ0均为正,其余情况类同。同时加入自变量l,即接触点与孔截面之间的距离,l0即为初次接触时的距离。计算可得

式中:FX为柔顺进给机构的侧向力,FZ为进给力,M为弯矩。接触点的压力为N1,摩擦因数为μ,摩擦力为μN1。同时,由于角度偏差θ通常小于2°,所以可以进行一定程度上的化简。综上,可以推导出这一阶段的受力模型。
几何方程

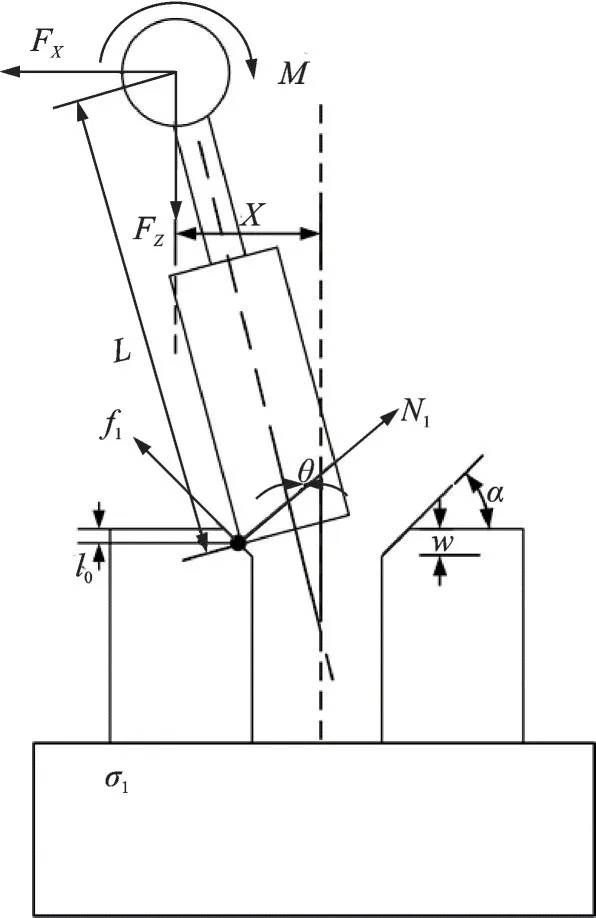
图13 通过倒角阶段示意图Fig.13 Schematic of going through the chamfer stage
受力方程

最大正应力方程
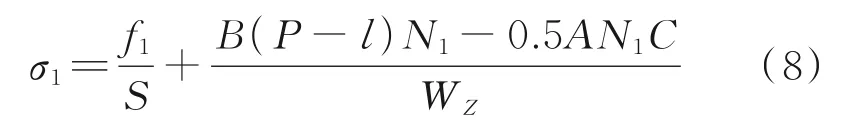
物理方程

式中:Kθ和KX为整个柔顺进给机构的转向刚度和侧向刚度。最后联立方程解得

式中:FX、M、FZ、N1均为自变量l的一元函数,且

2.2.2 单侧面接触阶段
单侧面接触的情况下,各个部件参数及受力情况如图14 所示。耳片受到的压力N1和摩擦力f1分别垂直和平行于耳片的表面。同时,为了区分各个阶段,定义新的自变量l1=l-w,即下端面到倒角下沿的距离。

图14 单侧面接触阶段示意图Fig.14 Schematic of single side contact stage
同理,几何方程
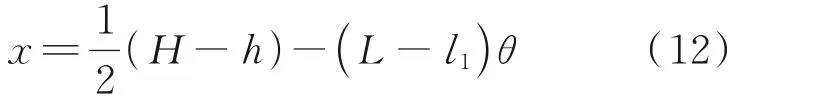
受力方程

最大正应力方程物理方程


最后联立方程解得
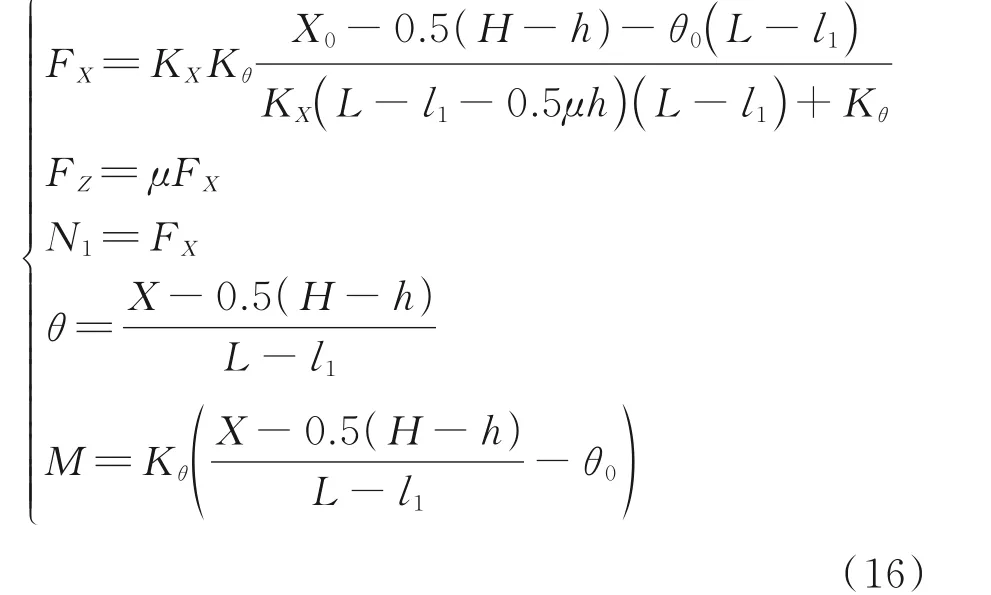
式中

2.2.3 双侧面接触阶段
双侧面接触的情况下,各个部件参数及受力情况如图15 所示。同时,为了区分各个阶段,定义新的自变量l2=l-w,可以列出如下方程。
几何方程

受力方程

最大正应力方程

物理方程

最后联立方程解得


图15 双侧面接触阶段示意图Fig.15 Schematic of double side contact stage
对双侧面接触阶段进行建模时,需要研究单侧面接触与双侧面接触的临界情况,即临界距离ls:由于此时处于单侧面与双侧面接触的极限位置,此时的支撑力N2=0,如图16 所示。
将上述条件代入,化简得到

式中

根据韦达定理求解式,再结合实际情况,可得

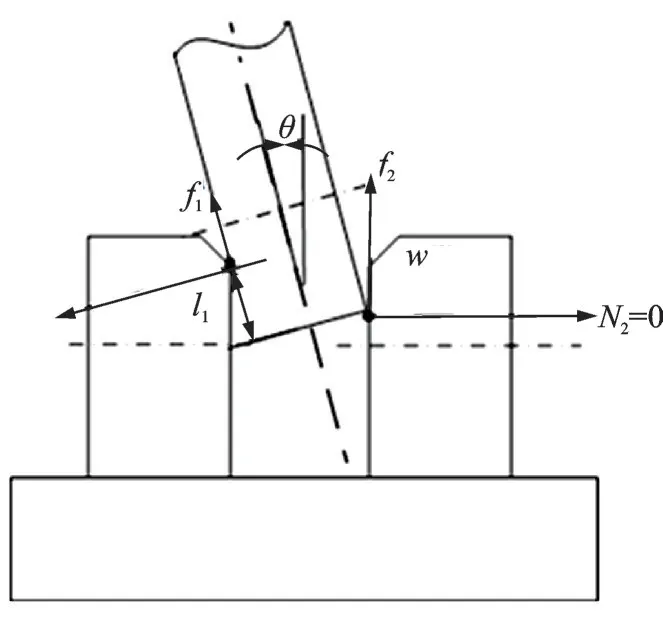
图16 单侧面接触与双侧面接触临界状态Fig.16 Critical state of single side contact stage and double sides contact stage
至此,得到了叉耳式连接结构柔顺对接全过程的接触力模型。选取模型结构参数h=32.95 mm,H=33 mm,D=70 mm,c=15 mm,L=60 mm,Kθ=2.08×108N·mm/rad,KX=560 N/mm,w=2 mm,α=45°初始偏差θ0=0.05°,X0=0.5 mm。绘制出对接装配过程中N1、N2、σ1、σ2与进给深度l曲线,如图17 所示。

图17 接触过程仿真分析结果Fig.17 Simulation analysis results of contact process
图17 中,虚线A表示叉耳式连接结构对接过程进入倒角接触阶段,虚线B表示进入了单侧面接触阶段,虚线C表示进入了双侧面接触阶段。根据图17 中的压力和应力曲线可以看出:当叉耳式连接结构对接过程处于倒角接触阶段、单侧面接触阶段时,不管是接触力还是应力都相对较小;进入双侧面接触阶段后,接触力和应力快速增大,后来随着叉耳式结构相对位姿的不断修正,接触力、应力呈先增后降的趋势。
2.2.4 最大接触力预测
基于上述模型,分析在初始偏差X0、θ0确定后,对接过程中接触力N1、N2的最大值,与关键结构应力水平σ1、σ2的最大值。由于N1、N2、σ1、σ2的最大值均发生在双侧面接触阶段。故针对这个阶段的N1、N2、σ1、σ2求导,得到


σ2相对复杂,可以通过遗传算法求解对接过程中的最大值。

因此,在机翼部件对接进行之前,可以根据装配工装的工艺参数,通过初始偏差X0、θ0直接对装配过程中关键结构的最大受力、应力N1max、N2max、σ1max、σ2max进行预测,如果预测值超过设定阈值则继续调整姿态。即通过上述公式,可以根据装配工装、工艺要求对初始偏差X0、θ0进行更科学的限制,避免了对接装配过程因接触力过大而造成连接结构表面损伤、应力过大的情况。
2.3 有限元分析验证
本节对五自由度柔顺机构叉耳式结构对接过程进行有限元建模分析,并对该数学模型的进行验证。
2.3.1 材料设置
根据实际项目的需求,作为接触力分析的主要研究对象,叉耳式连接结构的材料为0Cr13Ni8Mo2Al 钢。这种钢材使用双真空冶炼工艺,是一种高强度的沉淀硬化不锈钢。这种钢材的性能优良,除了具有较高强度外,还有良好的断裂韧性、横向力学性能。鉴于这种钢材良好的综合性能,在宇航、航空航天和核反应堆等领域广泛应用。根据《不锈钢实用手册》,材料密度为7.76×10-9t/mm3,杨氏模量为195 000 MPa,泊松比为0.278。其余部件由于不是本次分析的主要研究对象,近似选取45 号钢作为材料。
2.3.2 有限元模型构建
考虑到本章主要研究对象为柔顺对接过程中叉耳结构的受力情况,主要与五自由度柔顺对接机构在对接过程中各自由度方向的运动位移、相应弹簧的刚度相关。且柔顺机构在设计时已经进行过校核,对接过程中各部件(除弹簧等柔性部件)几乎不发生形变。考虑上述几点,本章基于模型运算能够收敛的条件下,以提高接触力分析精度、最大程度还原五自由度柔顺机构特性为目的,对五自由度柔顺机构有限元模型进行了如下简化:(1)机构运动学特性直接影响着对接过程中叉耳式连接结构的接触力大小,因此必须还原:保留了4-RPS 运动机构。同时由于直线导轨与转动导轨结构复杂且辅助设施繁多,引入模型后会导致运算不收敛,但直线导轨与转动导轨的运动学特性简单,因此在模型中删去相关部分,采用Abaqus 软件中的connector 功能实现。(2)为了使整个模型运算得以收敛,必须要删去部分与接触力无关的部件:如螺栓、螺柱等大量为连接、支撑、固定而安装的部件。(3)原机构考虑到承载能力、稳定性、自重和便于安装等因素,为部件设计了许多复杂特征,如加强肋、孔和倒角等,这些特征不会影响连接结构的接触力大小,但会导致网格划分质量降低、大大提高模型的运算难度,因此在建模时删掉了这些特征,合理地将部分部件转化为形状规则的部件。
根据上述原则,本章最后保留了固定底板、上底板、4 组RPS 运动机构、托架过渡件、机翼部件和对接组件等主要运动部件,省略了下底板、导轨等辅助部件,将部分不发生相对运动的部件进行合并,删除了螺栓螺柱等部件,并适当调整柔顺机构外形。如图18 所示。
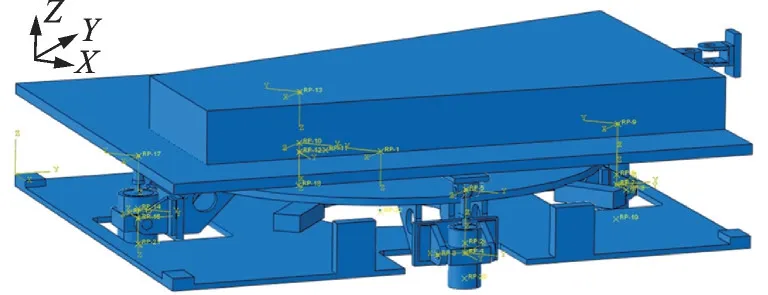
图18 五自由度柔顺对接机构有限元模型构建Fig.18 Finite element model construction of five degrees of freedom compliant docking mechanism
设计模型的运动学关系时,采用连接器与弹簧元件来实现五自由度柔顺机构的运动学特性:连接器还原各部分之间的相对运动关系、弹簧元件还原各组件之间的柔性。弹簧参数方面:(1)固定底板与托架过渡件之间的竖向拉伸弹簧,共4 组,每组4根,每根劲度系数为10 N/mm。(2)固定底板与上底板之间的斜向拉伸弹簧,共4 组,每组6 根,每根劲度系数为10 N/mm。(3)位于导向套内,连接导向套与导向柱之间的碟簧,共4 组,每组1 根,每根劲度系数为100 N/mm。设置弹簧单元时,将每组弹簧合并为一根,因此在有限元模型中共包括12 个弹簧单元:位于固定底板与托架过渡件之间的4 个劲度系数K1=40 N/mm 的弹簧、位于固定底板与上底板之间的4 个劲度系数K2=40 N/mm的弹簧、位于导向套内部的4 个劲度系数K3=100 N/mm 的弹簧。根据公式(2),可以计算出各个自由度方向上的等效刚度。

2.3.3 其余参数设置
结合本模型的运动学特性:对接过程中在弹簧、弹性连接器的作用下柔顺对接,所以对接过程中分析步选用动力隐式分析步。
由于该模型运动特性复杂,仿真过程不易收敛。为了更容易收敛,在动力隐式分析步之前加入一个静力通用分析步,在静力通用分析步中沿对接方向加入一个小的位移,让对接部件先有一个较小的接触。此外,由于研究对象为叉耳式连接结构在对接过程中的接触力大小,为了仿真过程更加容易收敛,设置边界条件时:将固定底板完全固定,机身沿对接方向与机翼进行对接。此外,将对接过程中不会发生运动的运动方向完全固定,避免出现无法收敛的情况。
相互作用方面,选用surface-to-surface 接触。根据经验,设置对接件之间的摩擦系数μ=0.1。
网格划分的质量关系到模型储存空间、运算速度和模拟精度。因为本次研究对象为叉耳式连接结构对接过程中关键结构的力学特性,同时整个机构运动特性复杂,所以对固定底板、上底板、托架过渡件和4-RPS 运动机构采用四面体网格,并指派C3D10 类型单元。叉耳式连接结构作为主要分析对象,采取六面体网格,指派C3D8R 类型单元,并进行更精细的网格划分。
2.3.4 有限元结果分析
此次分析的初始偏差为θ0=0.04°,X0=1 mm,部件结构的主要参数为:h=32.95 mm,H=33 mm,D=70 mm,c=15 mm,L=60 mm。本次分析结果如图19 所示。
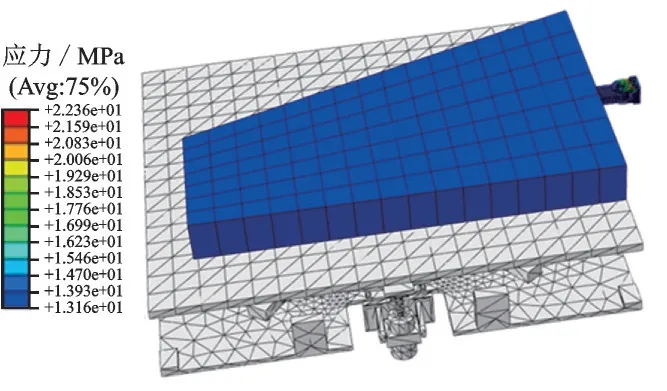
图19 有限元分析结果Fig.19 Finite element analysis result
由图17 可知,对接过程中σ1的数值一直大于σ2,因此决定对σ1的结果进行分析验证。获取叉耳式结构根部危险截面应力最大值σ1的仿真结果时,主要选取根部中央的点(6 个),对边缘区域的结点采取抽样的选取形式(4 个),共选取10 个节点。如图20 所示。
上述结点在柔顺对接过程中的应力变化情况与理论值如图21 所示。
根据上述结果,可以得出下列结论:

图20 结点选取Fig.20 Node selection

图21 σ1 理论值与有限元分析结果Fig.21 Theoretical value of σ1 and finite element analysis results
(1)建模过程中σ1为危险截面最大应力值,从图21 中可以看出,进给过程中截面单元应力最大值约为25 MPa,与理论分析一致。
(2)仿真应力结果与理论值并不完全一致且呈现反复波动的情况,这主要是由于对接装配过程中接触面之间存在着一定卡塞现象。
3 结论
通过研究柔顺对接机构运动原理、等效刚度和结合叉耳式连接结构的特点,建立了叉耳式连接结构在柔顺对接过程中的接触力模型。该模型可以依据柔顺机构等效刚度、连接结构尺寸参数、对接前位姿偏差,对柔顺对接过程中的接触力大小进行预测。最后,通过有限元分析对该模型的正确性进行了验证。分析结果表明,叉耳式结构根部存在最大应力。在装配过程中,应根据接触力模型分析调整机翼位姿,避免连接结构在对接过程中出现磨损和变形。
本研究首次提出将装配过程划分为4 个阶段并建立分段接触力模型,预测出最大接触应力大小和位置,实现在机翼调姿定位结束后、对接开始之前的“接触力计算校验”,优化了翼身数字化柔性对接装配过程。此外,该模型还可以根据调姿数控定位系统的位姿精度,指导柔顺平台的设计。

