一种低耦合高精度六维力传感器设计及应用

宋 逸，段晋军，相立峰，李 晨，姚举禄，戴振东

（1.南京航空航天大学机电学院，南京 210016；2.南京神源生智能科技有限公司，南京 211215）

全球新一轮科技革命和产业变革正在加紧孕育、兴起，自动化、智能化是以制造业为代表的现代工业发展的重要趋势。现代工业的自动化、智能化发展进程离不开信息传感系统的支撑。中国《智能制造发展规划》中指出，要“聚焦感知、控制、决策、执行等核心关键环节，推进产学研用联合创新，攻克关键技术装备，提高质量和可靠性”［1］。

接触过程几乎贯穿了现代加工、制造业的所有环节。因此，对以“接触载荷”为代表的力和力矩的准确、快速测量是实现加工、制造智能化的重要保障［2］，是智能设备和机器人实现柔顺化、智能化操作的关键技术挑战之一［3-4］。传统的力（矩）测量多依靠单分量或少分量的传感器实现［5］。但随着设备工作条件和工作模式的日益复杂和智能化需求的日益突出，现代工业设备对力传感和控制要求也越来越高：需要在兼顾尺寸要求的基础上，精确快速感知三维空间作用力和三维空间力矩，并实现反馈控制。因此，迫切地需要发展集成化的高性能六维力（即三维力＋三维力矩）传感器。

西方科技强国早在20 世纪70 年代就展开了多维力/力矩传感器的研发工作，积累了丰富的技术能力和应用经验［6-9］。近年来，中国不少专家学者也正在加紧对多维力/力矩传感器（特别是针对特殊用途的多维力传感器）的研制［10-15］。相较于因原理和结构限制而较难用于多维力/力矩测试的电容式和电感式传感器以及因静态性能较差而无法在多场景使用的压电式传感器，电阻应变式力传感器能够广泛兼顾不同需求，是目前大多数研究者的首选。

电阻应变式传感器设计的核心之一是弹性体设计。兼顾高灵敏度、高动态性能和低维间耦合的原理和结构创新是当前电阻应变式多维力传感器研制中面临的一大挑战。高灵敏度要求应变测量区域的刚度尽可能小而易于产生应变，而高动态性能则通常要求整个结构的刚度尽可能大。此外，结构上的连续性导致弹性体各区域之间在受外载荷时不可避免地会产生耦合变形（应变），进而可能导致耦合输出。因此，平衡静/动态性能、同时尽可能地消除各个测量方向之间的耦合是电阻应变式多维力传感器研究设计中必须重点关注的问题［16］。

为实现打磨机械臂等智能工业设备作业过程中载荷的准确快速测量，本文设计研制了一种结构紧凑的钛合金电阻应变式六维力传感器。该传感器较好地实现了高灵敏度、高动态特性和低维间耦合的平衡。同时，该传感器中采用了一种新型的结构设计，可为其他多维力传感器研制提供新的思路。

1 六维力传感器弹性体构型设计

1.1 弹性体构型

本文中传感器弹性体在构型设计时采用了一种新型的多应变梁组合构型，如图1 所示。弹性体由外圈、中心台以及4 组应变梁组成。每组应变梁包含一根扁平梁和两根对称的“L”形梁。通过对梁的结构尺寸进行设计，在保障整体刚度的同时降低局部刚度、并突出不同应变梁在承担不同方向载荷上的优势，继而实现“高刚度、高灵敏度和低耦合”这一设计目标，同时保障弹性体结构加工和贴片的便捷性。

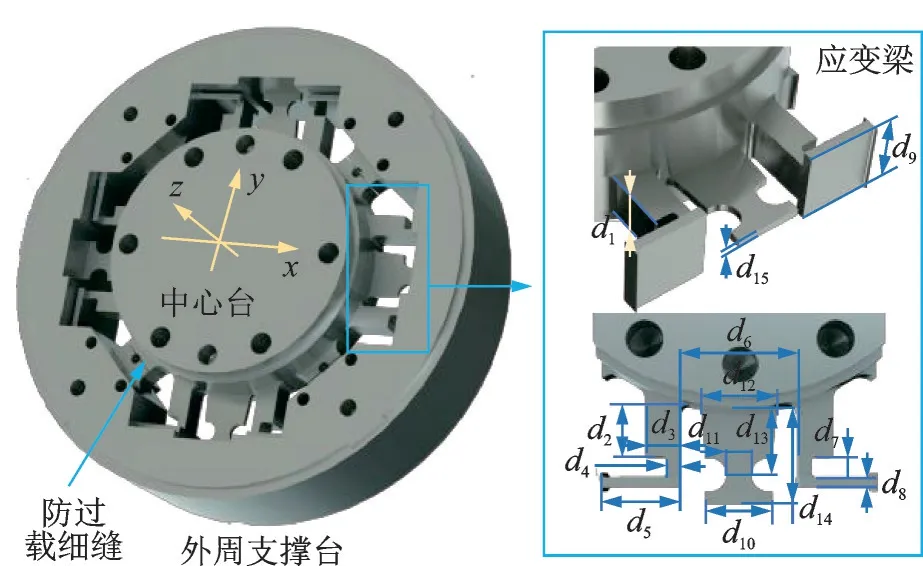
图1 六维力传感器弹性体结构示意图Fig.1 Elastic structure of the six-axis force sensor

1.2 弹性体受力分析

当弹性体受x方向的力时（图2（a）），a、b梁产生轴向拉伸（压缩）而c梁产生横力弯曲。但由于c梁沿x方向的厚度较小、抗弯曲刚度较小，沿x轴的力将主要由a梁承担。当弹性体受y方向力时，情形与受x方向力时相似。当弹性体受到z方向的力时，各应变梁载荷对称，可简化为沿z轴的力（图2（b））。但由于中心台和外圈的刚度比应变梁的刚度大得多，变形协调条件还将导致应变梁受到内弯矩作用。而“L”形梁在z方向的抗弯刚度较大，将承担主要弯矩。

当弹性体受到绕x轴的力矩Mx时，y方向的上下应变梁将受到弯矩作用，而x方向的左右应变梁则受到扭矩作用（图2（c））。y方向上抗弯刚度较大的“L”形梁b、c将承担主要弯矩。同样，当弹性体受绕y轴的力矩时，情形与受绕x轴力矩时相似。如图2（d）所示，当弹性体受到绕z轴的力矩时，x、y方向应变梁的受力情形相似，可简化为沿x或y方向的横力。由于“L”形梁的b部分和c部分连接位置厚度较小、抗弯刚度小，而扁平梁（a梁）沿横力抗弯刚度大，上述横力引发的弯矩将主要由扁平梁（a梁）承担，并且最大应力（变）位于扁平梁的边缘位置。

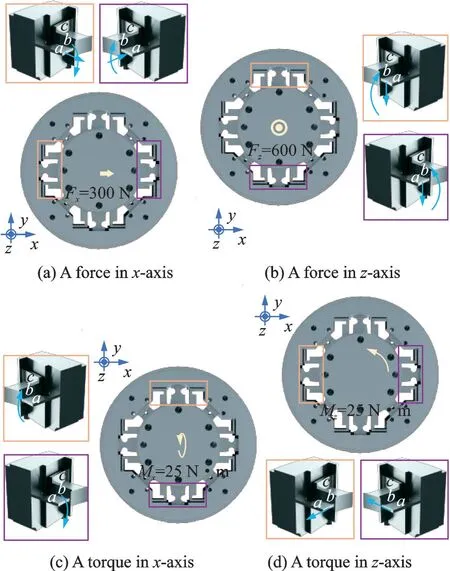
图2 弹性体受力分析简图Fig.2 Force analysis of the elastic structure

上述受力分析结果初步表明：通过设计组合梁的具体结构，可以在保障系统刚度的同时尽可能地降低各个方向之间的耦合。但其效果还有待于进一步分析验证。值得注意的是，上述受力分析的结果还初步指明了贴片位置选择和电桥设计方案。

2 弹性体结构仿真分析

为进一步明确上述弹性体的结构优势和具体尺寸参数，本文首先利用有限元法（Finite element method，FEM）对上述弹性体进行建模和静态加载的仿真分析。所用材料为钛合金TC4，弹性模量为E=120 GPa、泊松比为ν=0.34、密度为ρ=4 430 kg/m3、屈服强度不小于890 MPa。根据实际使用需求，传感器的量程设定为：横向力Fx=Fy=300 N，法向力Fz=600 N，三轴扭矩Mx=My=Mz=25 N·m，最大外径为95 mm，中心台的直径为51 mm。模型中应变梁采用8节点六面体单元，中心台和外圈采用四面体单元。弹性体外圈下表面为固定约束，中心台上表面中心点处施加集中载荷。经过多次迭代计算后，最终确定各关键部位的尺寸如表1所示。

表1 六维力传感器弹性体关键部位尺寸Table 1 Dimensions of key parts at the elastic structure of the six‑axis force sensor

按照上述尺寸和材料参数对弹性体结构的有限元仿真结果如图3 所示。考虑到弹性体结构为对称结构，x方向与y方向加载时结果相似，图3 中仅给出Fx、Fz、Mx及Mz单独作用时的结果。

当弹性体受到x方向300 N 的力时，最大应力为53.8 MPa（图3（a））。最大正应变区为x方向中间扁平应变梁最窄部分（图3（e））。左侧梁的上下表面均为拉应变，右侧梁上下表面均为压应变（图3（i））。当弹性体受到z方向600 N 的力时，最大应力为121.8 MPa。“L”形梁承担了大部分载荷。最大应力区在“L”形梁与外圈连接处（图3（b）），这可能是由于局部应力集中导致的。图3（f）给出了弹性体y方向正应变分布云图，图3（j）给出了y方向扁平梁上下表面中线上的正应变分布。仅受到y方向力时扁平梁上下表面正应变分布相同；而仅受到z方向力时扁平梁上下表面正应变分布相反。

当弹性体受到绕x轴的力矩时，载荷主要由y方向的“L”形梁承担。最大应力为282.8 MPa，同样出现在“L”形梁与外圈的连接区域（图3（c））。相应“L”形梁的y方向正应变分布如图3（g）所示，其中线上的应变分布如图3（k）所示。显然，“L”形梁上下表面正应变分布几乎相反。当弹性体受到绕z轴的力矩时，其应力分布如图3（d）所示，4 组应变梁上的应力分布相同，载荷主要由扁平梁承担。图3（h）示意了此时x方向扁平梁上的正应变分布，其边缘约1 mm 位置的应变变化规律如图3（l）所示。

有限元分析结果还表明：当弹性体各个方向均满载时，最大应力为455.3 MPa，小于钛合金屈服强度的一半。实际上，从图3 可以看出，在不同载荷最大应力几乎都出现在“L”形梁与外圈连接的角点处。因此，可以通过倒角等措施解决这些位置应力集中现象以进一步提高系统的过载性能。

3 应变片贴片、组桥设计分析

上述分析表明通过特殊的结构设计能够大大地降低该弹性体的耦合变形，但结构上的连续性导致结构耦合变形不可完全避免。因此，需要进一步通过贴片位置调整和电桥组桥设计来消除耦合。本文中使用从中航电测仪器股份有限公司采购的BF350-2.2AA（11）T8 型电阻应变片，基底尺寸为5.1 mm×2.4 mm，敏感栅尺寸为2.2 mm×1.8 mm。首先根据仿真得到的应变与结构表面位置相关性确定应变片的贴片位置（图3 下排灰色区域），然后进一步设计了图4 所示的应变片贴片及组桥方案。

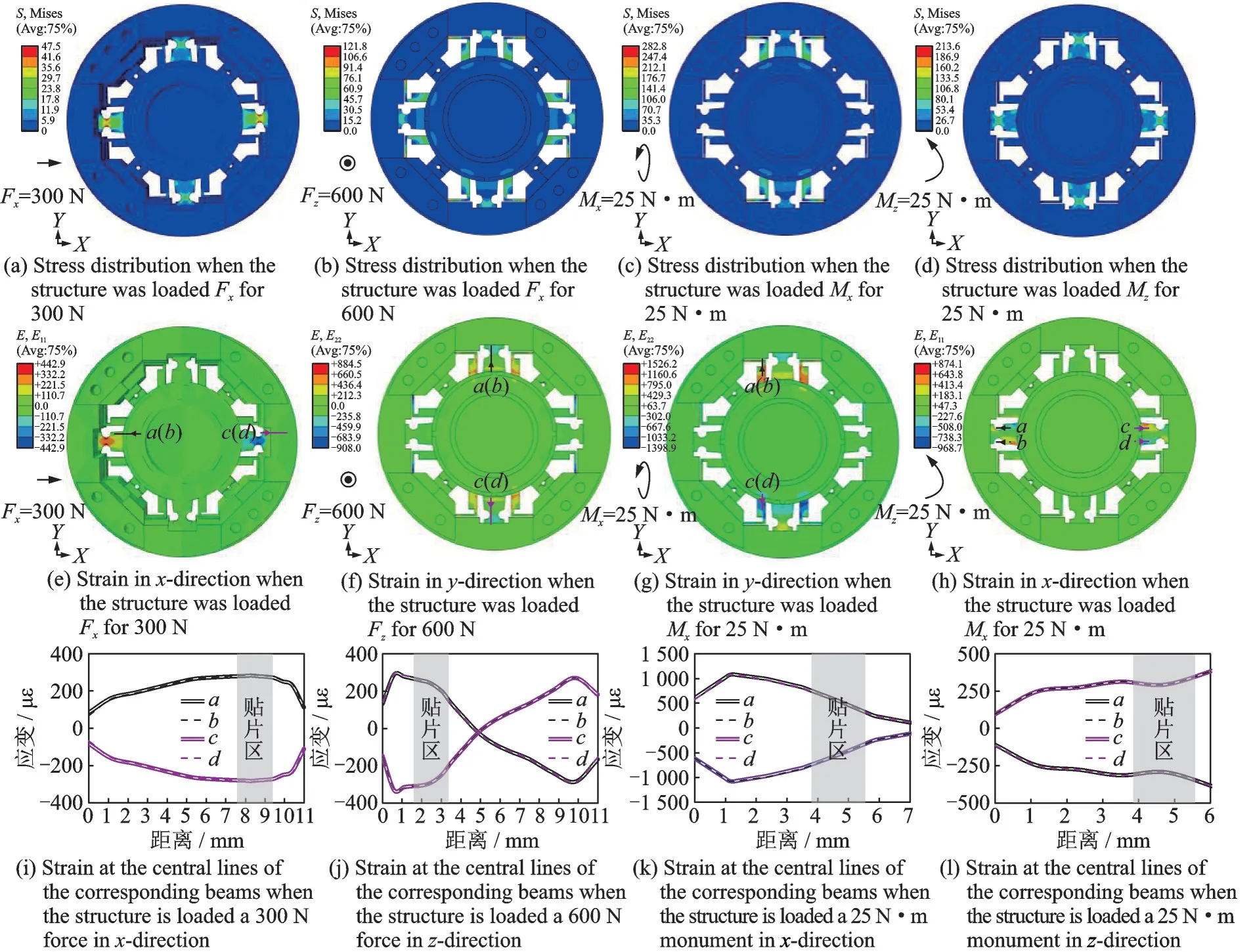
图3 弹性体有限元静力分析结果Fig.3 FEM analysis results of the elastic structure

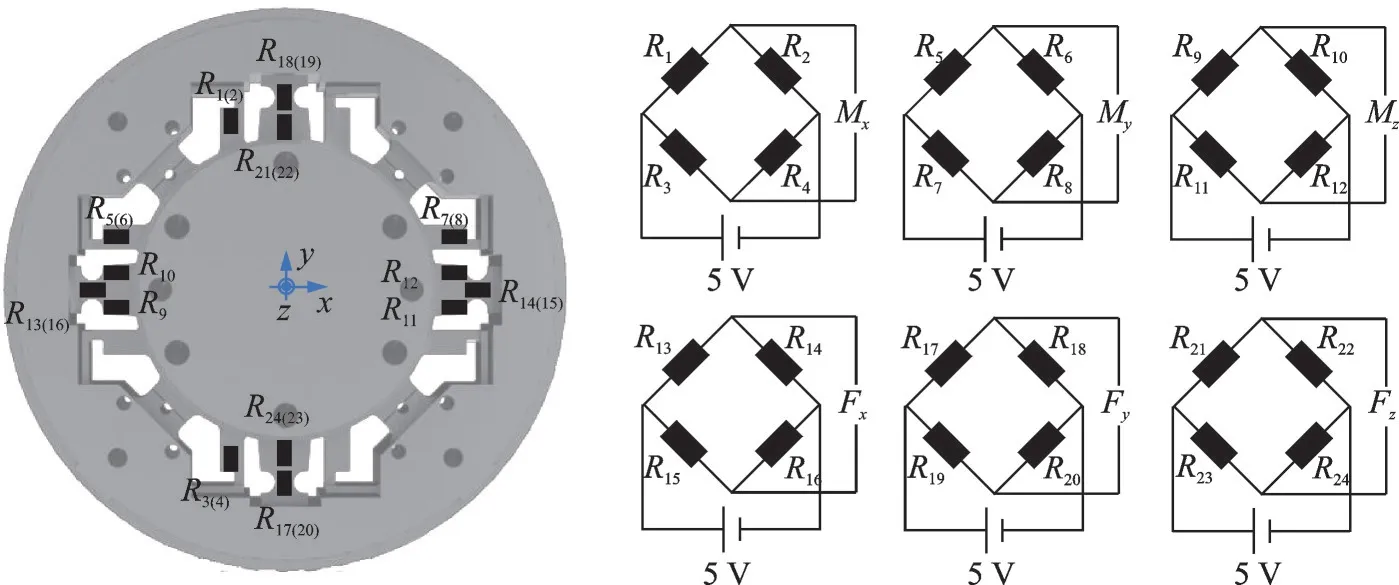
图4 应变片贴片及组桥示意图Fig.4 Diagram of strain gauge positions and bridges

以Mx的测量电桥为例对传感器解耦进行分析。在受到三维力和三维力矩作用时，用于测量Mx的应变片R1、R2、R3和R4在实际工作中感受的应变是x方向力引起的应变εFx、y方向力引起的应变εFy、z方向力引起的应变εFz、绕x轴力矩引起的应变εMx、绕y轴力矩引起的应变εMy、绕z轴力矩引起的应变εMz以及温度变化导致的应变εT叠加的结果。具体地，各应变片的读数应变可以写为

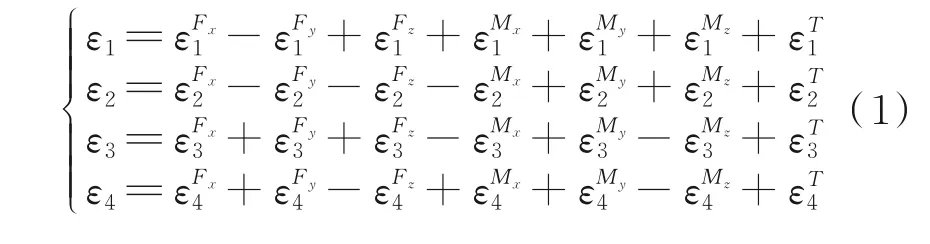
考虑到弹性体结构和内力的对称性（或反对称性）（图2），外载荷在对称位置引起的应变相同（或相反）。因此，电桥的读数应变最终可简化为

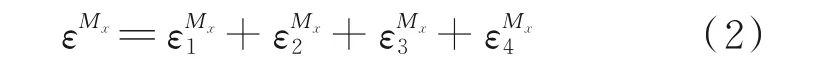
类似地，可以得到

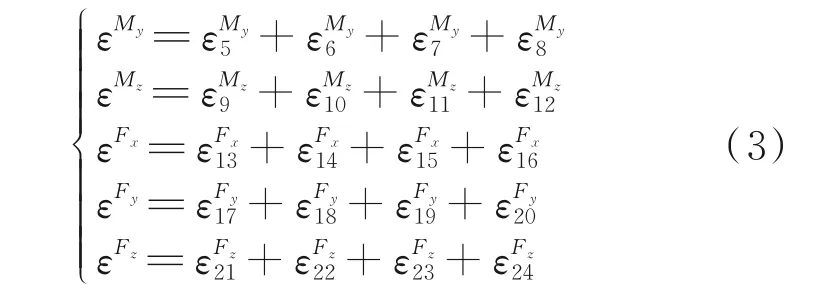
由此可见，通过合理的布片理论上可以完全消除各个方向之间的耦合。但实际情况下，由于加工误差、贴片位置偏差等因素的存在，各方向之间仍然可能存在耦合，需要进一步标定确认。

4 六维力传感器标定测试

4.1 静态标定

本文中根据上述分析试制了钛合金的六维力传感器弹性体，并对该六维力传感器进行贴片、组桥和静态标定。标定力时，将力传感器固定在刚性基座上，通过砝码沿各个方向分别加载（图5（a））。标定力矩时，采用了一种专门的力矩标定设备（图5（b）），将传感器固定后通过一对轻微偏置的拉杆向传感器施加力偶（图5（b））。拉杆末端各自连接了一对中航电测股份有限公司生产的精度为0.1‰的单轴拉力传感器，用于记录加载过程中实际的力，进一步计算力偶矩。如图5（b）所示的情形下，①③两只传感器受拉时向中心被标定传感器施加一个逆时针的力偶矩，而②④两只传感器受拉时将向被标定传感器施加一个顺时针的力偶矩。后端采用自研的信号调理放大采集模块进行信号处理采集，最终获得输出电压与标定载荷间的关系如图5（c）所示。

图5 六维力传感器静态标定曲线Fig.5 Static calibration of the six-axis sensor

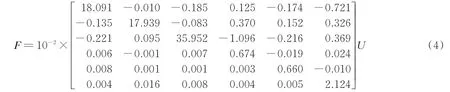
根据图5 的结果可进一步计算得到待测力F与传感器输出电压U之间的关系为

为评估传感器的耦合特性，本文中将除某一方向外的其余方向的载荷导致该方向的输出与该方向满量程输出比值绝对值的最大值之和作为该方向与其他方向的耦合Ej，即

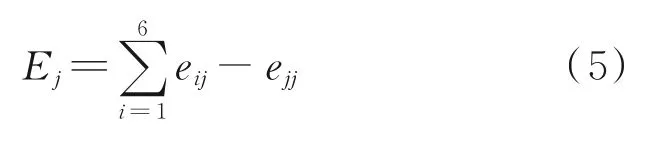
式中eij为第i方向加载导致第j方向的输出Fij与第j方向满量程输出FF j的比值的绝对值，即

参照式（4）中的矩阵解矩阵，可以估算该矩阵作用前六维力传感器的最大耦合为6.7%。将式（4）中的解耦矩阵作用到标定结果后进一步计算发现，经过解耦处理后的维间耦合小于1%。经过解耦矩阵作用后，将某一方向在不同载荷作用时的实际输出与相应载荷的差值记为Δ，重复标定标准差记为σ，则该方向的测量精度取为(max |Δ|+ 3σ)。根据计算，该传感器精度不低于1‰。详细静态标定结果如表2所示。

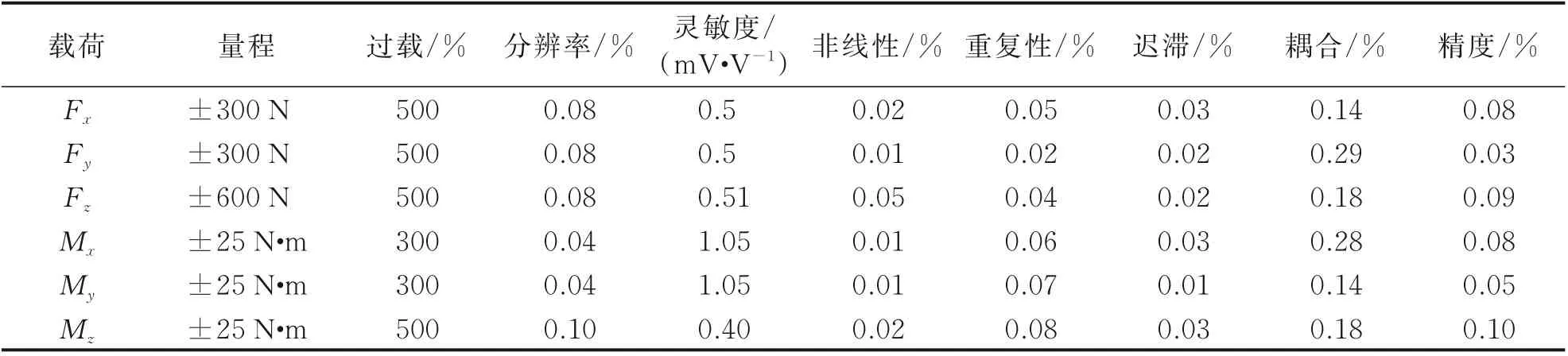
表2 六维力传感器静态标定结果Table 2 Static calibration summary of the six‑axis sensor

4.2 动态性能分析测试

动态特性是力传感器的另一重要参数［17］，但迄今为止国内外仍然缺乏统一的指标［11］。本文中通过模态研究来评估该传感器动态特性。

首先利用有限元法对该六维力传感器进行了模态仿真分析。传感器弹性体外圈下底面为固定约束时，其前三阶自由振动的振型特征和固有频率如表3 所示。

有限元仿真分析结果表明：该六维力传感器在z方向的固有频率最低，为2 402.2 Hz；而绕x轴和y轴转动振动的频率相当，约为3 330 Hz。由此可以推测该传感器z方向的动态性能最差。

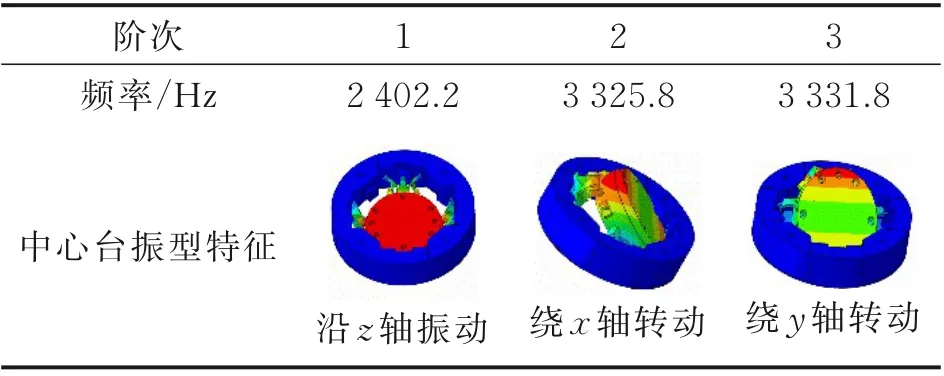
表3 六维力传感器弹性体模态仿真结果Table 3 Modal analysis result for the elastic structure of the six‑axis force sensor

在此基础上，本文进一步利用冲击响应法对该六维力传感器z方向的振动进行了测试，如图6（a）所示。为了保障采样率，此处使用了NI6255 采集板卡和SCXI1001 机箱以30 kHz 的采样率直接采集六维力传感器受瞬时冲击载荷后z方向的输出信号。测试结果表明，撞击结束后，系统发生欠阻尼衰减振动（图6（b））。通过对采集到的信号进行分析后发现该振动的阻尼振动频率为1 887.3 Hz（图6（c））。由于振动阻尼比极小，上述有阻尼振动频率几乎等于其固有频率。测试结果为理论计算结果的78.6%。这种差异可能是由于弹性体材料内部缺陷、装配等因素导致的。实际工作中，一般将传感器的工作频带设置为不超过其最低固有频率的一半（即943.7 Hz）以免引发系统共振。

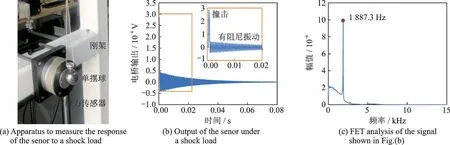
图6 六维力传感器动态测试Fig.6 Dynamic test of the six-axis sensor

5 应用测试

为进一步测试该六维力传感器的可用性，本文中将该六维力传感器用于打磨机械臂，测量打磨头与具有非规则表面工件之间的相互作用力（图7）。

图7 六维力传感器在打磨机械臂中的应用Fig.7 Application of the six-axis senor in a polishing robot

对于图7 所示的工件，为保证打磨效果及其一致性，手工初测确定打磨头与工件表面之间的法向接触作用力应该为12 N 并保持恒定。将上述六维力传感器安装至打磨机械臂测量打磨头与工件之间的相互作用力并实现机械臂的力反馈控制。当打磨头与工件表面接触时，法向接触力迅速增加至最大设定值（12 N）。机械臂开始跟踪曲面后，六维力传感器测量到了法向力的轻微变化并反馈至机械臂控制系统，使机械臂自主调整以实现恒法向力跟踪。

实际测试结果表明，该六维力传感器同时准确测量了抛光过程中的打磨头与工件表面相互作用时的三维接触作用力和力矩，并很好反馈至控制系统，保障机械打磨工作取得良好的效果。该应用一方面为进一步评估机械打磨操作提供了重要的数据支持，另一方面也证实了传感器的性能和可用性。

6 结论

本文设计了一种钛合金的六维力传感器，首先通过轮辐式组合梁结构设计来尽可能地降低各个方向之间的耦合，其次通过应变片贴片和组桥设计在理论上完全消除了各个方向的耦合。标定结果表明该六维力传感器具有良好的静态和动态性能，维间耦合小于1%，测量精度不低于1‰。实际应用验证结果表明了该六维力传感器的可用性，对提升中国多维力传感器技术具有重要意义，对其他用途的多维力传感器设计也具有参考价值。