一种可重构3‑RRR 平面并联机构及其工作空间分析
徐 帅,尤晶晶,2,叶鹏达,李成刚,沈惠平
(1.南京林业大学机械电子工程学院,南京 210037;2.南京航空航天大学江苏省精密与微细制造技术重点实验室,南京 210016;3.南京航空航天大学机电学院,南京 210016;4.常州大学机械与轨道交通学院,常州 213016)
“Robots”一词最早诞生于20 世纪20 年代,作为20 世纪最伟大的发明之一,机器人在生产生活及其他各个领域的应用已经成为一个国家的重要发展目标。智能机器人作为其中的一种典型产物,在满足自主设计、制造的同时,又要能完成复杂危险的任务,如焊接[1]、智能感知[2]和飞行器模拟[3]等。与此同时,传统并联机构,因机构构型的形式单一、功能简单且适应的工作环境相对固定,已经很难满足任务的需求[4]。而环境适应能力强与构型可变的重构并联机构,成为了学者们研究的热点问题[5]。当前,实现并联机器人重构的方法有4种:(1)切换主动与被动副模式[6];(2)施加关节运动约束[7];(3)改变运动副轴线方向[8];(4)锁合运动副[9]。基于此,本文采用了方法(4)的思想,设计了一种可重构支链,从而实现机构自由度或运动特性的改变。然而,并联机构结构上存在支链干涉和运动副转角约束的限制,导致动平台转动能力差和环境适应能力弱等问题。少自由度并联机器人由于驱动少、结构紧凑和结构独特等,吸引了国内外学者的研究[10],其中,三自由度平面并联机构最为典型。工作空间可以反映出机构的运动性能,是进行机构设计、运动规划的重要依据,也是进行尺度综合的基础。因此,研究并联机器人的工作空间具有十分重要的意义。
目前,数值法与迭代搜索法是求解工作空间常用的两种方法。文献[11]提出了一种具有平转解耦特性的3 球副移动副球副+3(球副移动副-虎克铰链)(3 spherical-joint,prismatic-joint,spherical-joint+3(spherical-joint,prismatic-joint-universal-joint),3SPS+3(SP-U))六自由度并联机构,结合柔性铰链回转空间及支链行程范围,采用边界离散点搜索法,得到了机构的位置和姿态可达工作空间。文献[12]以4-SPS并联机构为研究对象,运用数值法求解并绘制了机构的工作空间。文献[13]提出了一种新型可重构3-RRR球面并联机构,利用一个简单的4杆机构,结合杆长约束条件绘制了机构的工作空间。文献[14]提出一种可绕轴线转动的2-移动副可绕转轴线的转动副球副+移动副转动副可按需要工作或锁定 的 移 动 副(2-prismatic-joint r-revolute-joint spherical-joint+prismatic-joint revolute-joint locked prismatic-joint spherical-joint,2-PrRS+PR(P)S)变胞并联机构,采用Monte Carlo 法得到该机构的工作空间点云图。文献[15]基于机构结构降耦原理,提出了一种1-转动副转动副转动副转动副+2-转动副转动副转动副(1-revolute-joint revolute-joint revolute-joint revolute-joint+2-revolute-joint revolute-joint revolute-joint,1-RRRR+2-RRR)并联机构,建立了运动学正解数学模型,基于边界离散法得到了机构的工作空间。
本文提出了一种新型可重构三自由度平面并联机构。首先,利用运动副的锁合模式,实现3-RPR 型与3-RRR 型机构之间的切换;然后,以3-RRR 构型为例,基于方位特征(Position and orientation characteristic,POC)方程的并联机构拓扑设计方法[16],对该构型进行了拓扑特性分析。其次,基于运动学逆解模型,绘制了3-RRR 机构的位置工作空间。最后,基于杆长配比法,分析杆长行程变化对机构工作空间的影响。
1 三自由度构型设计
典型3-RPR 平面并联机构的结构简图和模型图,分别如图1、2 所示。它分别由正三角形形状的动平台0、定平台1 以及3 条结构相同的有序单开链(Single open chain,SOC)构成,且3 个分支运动链通常采用等边三角形对称布置,其中,每条SOC又由1 个移动副与固结于两端的转动副串联而成,可表示为-A⊥P⊥C‑(其中,⊥表示垂直,A、C为转动副,P为移动副)。

图1 3-RPR 平面并联机构结构简图Fig.1 Schematic diagram of 3‑RPR planar parallel mechanism
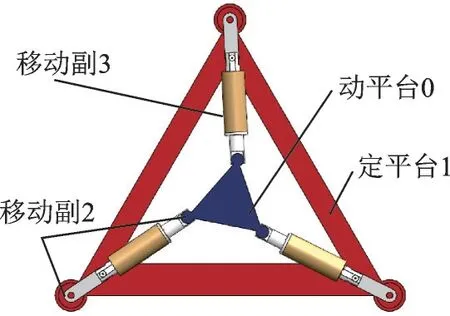
图2 3-RPR 平面并联机构结构模型Fig.2 Structural model of 3-RPR planar parallel mechanism
为了实现机构的重构,本文提出了一种可实现运动副锁合的可重构支链。不失一般性地,所提出的可重构支链驱动方式是依靠电机驱动,为了突出机构学原理,这里省略了驱动部件改为人为切换,简化后的结构模型如图3 所示。它主要由连杆1 与连杆2 两部分组成,其中,连杆2 主要由内套筒、外套筒和转换套筒构成[17]。

图3 可重构支链结构示意图Fig.3 Schematic diagram of reconfigurable branch chain structure
将连杆1 放置在内套筒的U 形插槽中,并通过螺栓和螺母连接,内套筒与外套筒通过螺纹进行传动。外套筒右端设置有凹槽,转换套筒左端设置有凸缘,凸缘放置在外套筒凹槽处。转换套筒与外套筒之间放置深沟球轴承,以保证相互之间独立转动,采用挡环进行轴向定位。
所设计的可重构支链具有2 种运动副模式:当连杆1 与内套筒通过螺栓与螺母紧配合时,旋转外套筒,带动转换套筒一起移动,此时支链为移动副模式。当连杆1 与内套筒松配合时,此时支链为转动副模式。
综上所述,将两种运动副模式分别应用在支链上,可得两类三自由度平面并联机构。即3 条支链同时设置为移动副模式,可得到一种3-RPR 平面并联机构,结构简图如图1 所示;同理,设置为转动副模式,可得到一种3-RRR 平面并联机构,结构简图如图4 所示。

图4 可重构三自由度平面并联机构简图Fig.4 Schematic diagram of reconfigurable 3-DOF planar parallel mechanism
区别于一般的3-RPR 平面并联机构,该机构不局限于一种工作模式。当机构运动出现奇异或工作环境发生改变,可转换为其他构型解决上述问题:如3-RRR 构型。
传统3-RRR 机构的杆件为固定长度,本文设计的机构的从动杆杆长可在一定的范围内变动,即为一种移动副装置。以构型3-RRR 平面并联机构为例,详细分析机构的拓扑结构特征及工作空间。
2 3‑RRR 构型的拓扑结构分析
方位特征集方法运算较为简单,易操作且物理意义明确,适用于无过约束机构和一般过约束机构的拓扑结构设计。基于机构的拓扑结构分析,可确定机构连续运动的拓扑特征,这些特征也是与运动学性能密切相关的非线性特征,如机构的POC、自由度(Degree-of-freedom,DOF)、耦合度等[18]。
2.1 机构的POC 集
用拓扑学符号来描述机构,可将机构中3 条支链用3 个单开链支路3-SOC{‑R|R|R-}表示,即可通过支路中运动副的维数来反映平面机构的POC 集。

式中:SM为运动副的POC 集;JiM为第i个运动副的POC 集;m为运动副的个数;PM为并联机构的POC 集;v为独立回路数;bMj为第j条支链末端的POC 集。
转动副的POC 集为R M=[t1;r1],据此,建立回路、机构的 POC 集。 对于支链 SOC1{-A1|B1|C1-},有

同理,SOC2与SOC3的POC 集分别为

进一步,确定机构的POC 集为

2.2 机构的DOF
具有v个独立回路的机构可视为由(v+1)条支链组成,因此可确定机构v的个数为2。进一步,可确定该回路与机构的自由度。确定SOC1与SOC2组成的第1 回路LOOP1:{-A1|B1|C1|C2|B2|A2-}的自由度为

由LOOP1与SOC3构成的第2 回路LOOP2:{-A3|B3|C3-},可确定机构的自由度为

2.3 机构的耦合度
根据有序SOC 的机构组成原理[19],该机构的两个单开链回路约束度,可通过回路1、2 分别求出。

机构的耦合度为

这样,该机构包含1 个SKC,机构的耦合度κ=1。
2.4 位置反解模型
2.4.1 机构的坐标系建立及其参数标注
建立机构的坐标系及其参数的标注,如图4 所示。该机构定平台1 上3 个顶点处的转动副几何中心分别记作A1、A2和A3,动平台0 上3 个顶点处的转动副几何中心分别记作C1、C2和C3。P为动平台外接圆的圆心,其半径为a;O为定平台的外接圆圆心,其半径为b,O‑xy为全局坐标系,x轴平行于lA1A2,y 轴垂直于lA1A2。其姿态角γ为lC1C2与x轴正向的转角,驱动杆杆长Ai Bi=l1(i=1,2,3,下同。),从动杆杆长Bi Ci=l2,θi、βi分别为机构的驱动角与从动角。
2.4.2 运动学逆解
平面机构运动学逆解,就是利用机构的姿态反求各杆件的位置和姿态[20]。对于3-RRR 平面并联机构来说,即用表示动平台位姿的3 个输出参数xp、yp及γ,求输入角θi。已知定平台的边长,由几何关系可确定A1、A2、A3点在定坐标系中的坐标为

C1、C2、C3在定坐标系中分别表示为

由于3-RRR 并联机构动平台ΔC1C2C3在平面x y内运动,其系统结构参数具有对称性,因此选取一条支链对其分析,其他两条支链原理上相同。对于第一条支链,根据闭环几何约束条件可得到
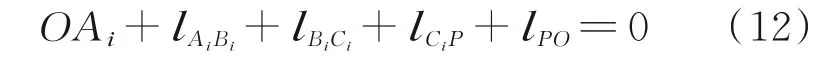
将式(12)分别在x、y轴上投影展开为

已知A1、C1及P点的坐标,可将式(13)进一步化简为

式中

两个约束方程存在两个未知数θi、βi,将式(14)等号两边平方,并作相加处理,可消去βi得到方程为

进一步,求解式(16)可得

至此,已构建了3-RRR 平面并联机器人的位置反解模型。
3 3‑RRR 构型的工作空间分析
并联机构的工作空间是指动平台所能运动到空间上所有轨迹点的集合[21]。传统分析机构工作空间的方法,基于机构的运动学逆解,采用二维搜索法得到机构的位置工作空间图,其方法简单、便捷。基于此,结合杆长行程变化对工作空间的影响,研究工作空间的几何特性。
3.1 支链的工作空间
假设第i条分支运动链在动平台中心处断开,此时的运动链可以看作串联机器人,支链末端点在工作空间上的点集,称为支链工作空间。选取第1支链作为支链工作空间的分析,如图5 所示。其中,杆长lB1C1可在一定的范围内运动。
以A1为中心作支链扫过的区域,记为第1 类支链工作空间,如图6(a),其外半径为

内孔半径为


图5 第1 分支链Fig.5 The first branching chain
显然,当杆长l1≤l2时,机构工作空间不形成空洞,而当A1副的转角受到约束时,子工作空间形成1 个扇形区域,记为第2 类支链工作空间,如图6(b)。
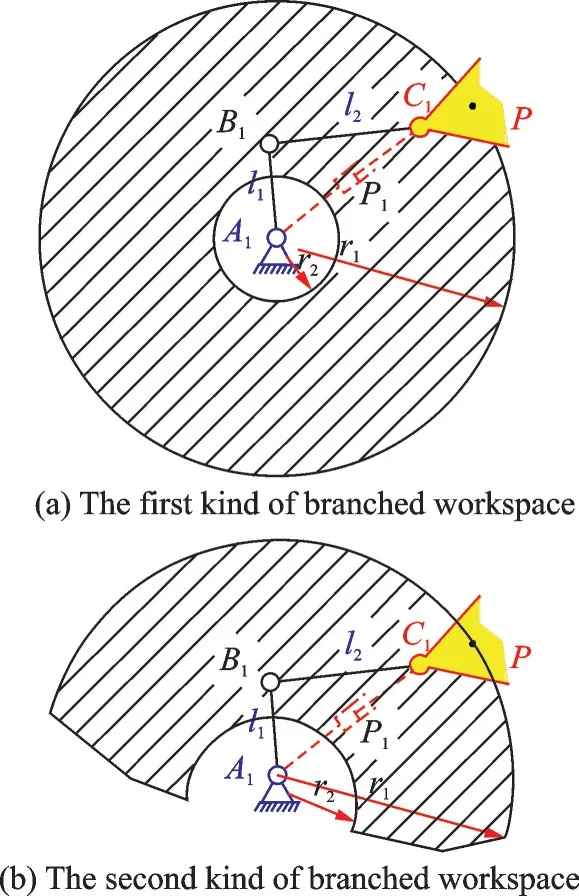
图6 支链工作空间Fig.6 Branched chain workspace
3.2 位置工作空间
机构动平台有3 个输入参数xp、yp及姿态角γ。当γ为定值时,只考虑支链1 的约束,参考点P的运动范围可由支链工作空间沿lC1P移动得到;当考虑3 条支链的约束时,满足3 条支链工作空间分别沿着Cj P(j=7,8,9)平移,可得到3 条支链工作空间的交集部分,即为机构的位置工作空间,设置动平台边长a=160 mm,定平台边长b=300 mm,如图7 中绿色区域。
3.3 杆长行程分析
支链的杆长行程变化,对应的位置工作空间形式存在一定的差异。在此基于运动学逆解模型,选取γ=0 rad,分析杆长对机构位置工作空间的影响。
(1)主动杆l1与从动杆l2不相等。设置l1=120 mm,l2=160 mm,得到的位置工作空间如图8所示。
(2)主动杆l1与从动杆l2相等。首先,设置l1=l2=160 mm,得到的位置工作空间如图9(a)所示;接着,设置l1=l2=120 mm,得到的位置工作空间如图9(b)所示。

图7 3-RRR 机构位置工作空间Fig.7 3-RRR mechanical position workspace

图8 第1 类位置工作空间Fig.8 The first kind of position workspace

图9 第2 类位置工作空间Fig.9 The second kind of position workspace
由图9(a)显示,l1、l2的杆长分别为160 mm 时,机构的工作空间大于第1 类机构位置工作空间。由图9(b)显示,l1,l2的杆长分别为120 mm 时,机构的位置工作空间最小。
(3)设置主动杆l1=120 mm,120 mm≤l2≤240 mm。鉴于从动杆杆长行程较大,在不影响杆长变动范围内,分别选取杆长的最小值、中间值及最大值作为研究对象,画出对应的位置工作空间,分别如图10(a~c)所示。

图10 第3 类位置工作空间Fig.10 The third kind of position workspace
从图10 可以看出,在120 mm≤l2≤180 mm时,机构的位置工作空间随着从动杆杆长的增大而增大;在180 mm≤l2≤240 mm 时,机构的位置工作空间随着从动杆杆长的增大而减小。结果表明,当从动杆杆长选取为主动杆杆长的1.5 倍时,此时3-RRR 并联机构的位置工作空间最大。
4 结论
本文通过设计一种可重构支链,提出了一种新型可重构三自由度平面并联机构,并计算分析了其工作空间。主要研究结论如下:
(1)实现了3-RPR 型与3-RRR 型平面并联机构之间的切换,为解决传统三自由度平面并联机构杆长尺寸固定、构型单一等问题,提供了一种新的方案。
(2)以3-RRR 型平面并联机构为例,分析了机构重要的拓扑指标值;建立机构的运动学逆解,并研究了杆长行程变化对工作空间的影响。
(3)基于运动学逆解模型,分析杆长行程变化对位置工作空间的影响。结果表明,当从动杆杆长选取为主动杆杆长的1.5 倍时,并联机构的位置工作空间最大。

