由“知识本位”到“能力习得”

丁晓丹

【摘 要】《义务教育数学课程标准（2011版）》将“运算能力”作为十个核心词之一，足见计算教学在数学学习中的重要性。日常教学中，我们经常发现教师把计算教学错误地演变成了知识传授。这样，学生虽然能将计算能力掌握得比较扎实，但却不能很好地举一反三、关联思考，更没有帮助学生形成良好的自学能力。因此，有效帮助学生从“知识本位”走向“能力习得”是计算课的灵魂。

【关键词】小学数学 计算教学 “知识本位” “能力习得”

“知识本位”是知识选择时的一种取向，它将知识的传授和灌输等同于教育本身，已将教育概念狭隘化。这种教育方式恰恰与学生学习能力及核心素养的培养背道而驰。但在日常教学中，经常出现这样的现象，教师错误地把知识的教学演变成知识传授。这样一来，学生或许对知识本身已牢固掌握，但却不能很好地举一反三、关联思考，更无法帮助学生形成良好的自学能力。因此，帮助学生从“知识本位”走向“能力习得”显得尤为重要。教学中教师应注意哪些问题呢？下面笔者将以苏教版数学三年级下册“两位数乘两位数的笔算（不进位）”为例，谈谈计算教学中如何帮助学生从“知识本位”走向“能力习得”。

本单元的笔算乘法分不进位和进位两个层次编排。本课属于不进位笔算乘法，它不仅为之后学习进位的两位数乘两位数、三位数乘两位数的笔算乘法奠定基础，而且为解决新问题的口算、笔算、估算提供经验。教师在教学中不能只关注计算结果，更应让学生充分经历探究过程，沟通多样化的算法与笔算之间的关系，在体会算理的过程中学会思考，习得方法并解决问题。基于此，笔者以“问题引领—自主探究—序列交流—能力提升”为线索进行了如下实践。

一、问题引领，初步感知

基于以上思考，笔者首先从学生已有知识经验出发，循序渐进地出示主题图，着力激活学生对“两位数乘一位数、两位数乘10的口算”的已有认识，激起学生对于新知的探究欲望。

教学片段：

师：同学们，秋天到了，看，迷你南瓜大丰收了！我们一起来看。

（出示2箱南瓜，每箱24个）

师：从图中你知道了什么？

生：有2箱南瓜，每箱24个。

师：这里一共有多少个南瓜，你会列式计算吗？

生： 24×2=48（个）。

（出示动画情境：又搬来了8箱同样的南瓜）

师：现在，一共有多少个南瓜呢？

生：24×10=240（个）。

（出示动画情境：又搬来2箱）

师：现在共有多少箱？

生：12箱。

【思考】借助动画情境，逐步呈现教材主题图，一方面激起了学生的学习兴趣和探究热情;另一方面引领学生回顾旧知，复习了“两位数乘一位数、两位数乘10的口算”，为本课内容的学习奠定基础。

二、法理互融，深入探索

本环节旨在探究两位数乘两位数笔算的算法及算理。教学中经常有教师重视方法多样化而轻视竖式笔算乘法的算理，忽视了沟通它们之间纵向联系的过程，导致学生对列式笔算乘法只停留在机械模仿层面，而并未真正理解竖式书写中每一步的含义，变成了“知识本位”教学。因此，教学中教师不仅要把握知识的来龙去脉，更要把握学生学习过程中的困难之处，做到有的放矢，教会学生习得解决此类问题的能力。

教学片段：

1.初步感知

师：看！12箱南瓜都打包好了，可小朋友却遇到了一个难题，你愿意帮助他吗？我们一起来读一读。

师：一共有多少个，你会列式解决吗？

生：“24×12”或“12×24”。

师：请大家估算一下，结果大约是多少呢？

生：200多。

师：你们是怎么想的？

生：把24看成20，12看成10， 因为20×10得200，所以正确结果比200大。

师：真棒！大约有200多个南瓜。

师：“24×12”到底等于多少呢？你想怎樣算？先想一想，再算一算。

生1：24×2=48（个），48×6=288（个）。

生2：24×6=144（个），144×2=288（个）。

生3：24×2=48（个），24×10=240（个），240+48= 288（个）。

【思考】因为有了上一环节丰富的认知经验，在探究“24×12”这一环节，笔者给予学生充足的独立思考和自主探究的空间。在学生自主探究之后，笔者首先逐一出示了前两种解法，并结合主题图沟通了两种解法间的联系;其次利用学生已有的“凑十法”的原始经验着重理解了第三种解法，为之后笔算算理的学习做铺垫。

2.探索算法

师：像这样，先算10箱南瓜的个数，再算2箱的个数，再合起来的方法在竖式笔算中也能体现！你会列竖式计算吗？

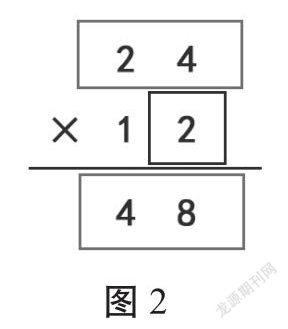
师：谁能看懂他先算了什么？（见图2）

生：先用个位上的2乘24，二四得八，二二得四，表示2箱南瓜有48个。

师：谁能跟他一样，再来说一说？

师：这里的240又是怎么得到的？（见图3）

生： 240算的是10箱南瓜的个数。

师： 10在哪里啊？

生：1在十位上，表示1个十。

师：哦！用十位上的1乘24，得到24个十，也就是240，这里的0可以省略不写。

师：最后他又怎么样了？（见图4）

生：把它们加起来。

师：把48和240加起来，得288，也就是求出了什么？

生： 12箱南瓜的个数。

师：将48和240加起来，加号可省略不写，而且要从最低位加起。

3.沟通算理

师：比较上面的口算和笔算过程，你发现了什么？

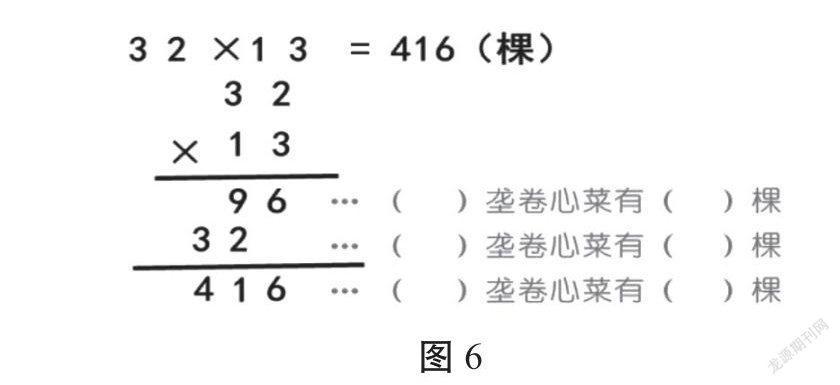
生：口算和笔算的第一步都是24乘2，算出2箱南瓜的个数;第二步都是24乘10算出10箱南瓜的个数，最后加起来。

【思考】本环节教学中，笔者让学生亲身经历了笔算乘法的探究过程，并有效突破了难点：第二步算什么以及格式要求。整个过程，笔者并没有急于教给学生笔算乘法的固定模式，而是用好了每个学生的知识经验及反馈的资源，三个层次的资源呈现也在序列交流中层层递进。这样便帮助学生合理建构起了口算与笔算乘法间的相互联系，做到算法与算理融合，也切实帮助学生习得此类乘法笔算的解决方法及相关算理，学会举一反三、关联思考。

三、专项训练，加深理解

1.计算练习

师：刚才通过大家的努力，我们帮小朋友顺利地解决了南瓜的难题。看！老师又带来了三个新问题，你们能用今天所学的方法算一算吗？

2.解决问题

师：同学们学得真快！再来看这样一个问题。

【思考】两个专项练习由易到难、循序渐进，目标都指向算法的掌握、笔算的验算以及算理的理解。在练习中帮助学生进一步巩固两位数乘两位数的算法，进一步体会算理，促进学生对算理的理解。在练习过程中学生可自主感知乘法的验算，运用交换乘数的位置再乘一遍的方法进行验算。

四、系统梳理，能力习得

师：以上这些就是我们今天的学习内容“两位数乘两位数的笔算”。学到这里，你认为笔算两位数乘两位数时，应注意些什么？

生：先用个位上的数乘，乘得的数表示多少个一;再用十位上的数乘，乘得的数表示多少个十;最后再把乘得的数加起来，而且要从最低位加起。还可以交换乘数的位置再算一遍進行验算。

师：同学们，其实我们不是第一次学习乘法了，让我们一起来回顾一下！（视频播放二、三年级所学的乘法知识）

师：数学就是这么有趣，前后知识都是有联系的。想一想，如果再继续往下学，我们将学几位数乘几位数呢？它们可以怎样算呢？能不能也用今天所学的知识来解释并解决呢？

【思考】在经历了笔算探究的整个过程之后，笔者引领学生经历从表内乘法到两位数乘两位数笔算的整个知识体系的过程，并借助追问“如果继续往下学，我们将学几位数乘几位数呢？它们可以怎样算呢？能不能也用今天所学的知识来解释并解决呢”，将知识进行系统梳理和沟通，把零碎的知识点串联成一条线，让学生感知数学知识的整体性，极大地激发了学生对后续学习的兴趣，有效地从“知识本位”成功走向了“能力习得”。

学生在教师的引领下充分经历并体验了“两位数乘两位数的口算（不进位）”过程，接着又在自主探究中建立起了口算与笔算间的纵向联系，掌握了算法，更明晰了算理，最后又通过合理猜想与类推，对“两位数乘两位数笔算”的算法及算理进行了合理的推广。这样的教学，不仅帮助学生建构起了数学知识的内在联系，更使学生明白了知识本身固然重要，学习能力的习得更是凌驾于知识之上的宝贵财富。因此，教师要以知识为载体，在帮助学生学得知识的过程中，提高学习能力，拓展学习理念，切实做到从“知识本位”走向“能力习得”。

【参考文献】

[1]李向阳.探讨核心素养下的小学数学计算教学实践策略[J].考试周刊，2021（12）.

[2]施乐旺.计算：要知“书”，更要达“理”——以“两位数乘两位数不进位笔算乘法”为例[J].小学数学教师，2018（10）.