Numerical studies of atomic three-step photoionization processes with non-monochromatic laser fields
Xiao-Yong Lu(卢肖勇), Li-De Wang(王立德), and Yun-Fei Li(李云飞)
Science and Technology on Particle Transport and Separation Laboratory,Tianjin 300180,China
Keywords: non-monochromatic laser field,bandwidth model,ionization yield,selectivity factor
1. Introduction
Compared with other unselective ionization methods such as surface ionization, plasma ionization, and electron/ion beam ionization, the atomic selective multi-step photoionization is characterized by high elemental/isotopic selectivity and high ionization efficiency. It has been used in many areas of science and technology where selective and efficient ionization is required,such as resonance ionization mass spectrometry (RIMS) for atomic spectroscopy and elemental/isotopic composition analysis of trace/ultra-trace samples,[1–3]resonance ionization laser ion source (RILIS) for radioactive ion beam production of isotope separator on-line facilities,[4,5]secondary neutral mass spectrometry (SNMS) for nuclear forensics,[6]and especially laser isotope separation(LIS),[7–9]which is regarded as a next generation isotope separation method after centrifugation.
In LIS,atomic vapor is excited and ionized by laser pulses generally. For common metal elements with an ionization potential of several electron volts, a three-step photoionization scheme is usually adopted for dye laser pulses within the visible range. Laser frequency is tuned to resonate with the target isotope precisely,exciting these atoms stepwise and yielding ions. The remaining isotopes are kept neutral basically due to isotope shifts. Subjected to an external electric field, the ions are extracted from plasma. Neutral atoms remain the previous direction. Thus, considerable ionization yield of the resonant isotope and selectivity factor, which is defined as the ratio of the resonant isotope’s ionization yield to the non-resonant isotope’s ionization yield, can be obtained. The LIS has been studied theoretically and experimentally for many elements, such as lithium,[10,11]calcium,[12]titanium,[13]nickel,[14]zirconium,[15]barium,[16,17]and a series of lanthanides and actinides.[18–27]It should be noted that both high ionization yield and high selectivity factor are required in LIS.Because atomic transition parameters are definite for a given photoionization scheme, and there is complicated interplay among systematic parameters, including laser parameters (Rabi frequencies, bandwidths, relative time delays, frequency detunings) and atomic Doppler broadening,the theoretical optimizations of systematic parameters are critical steps in LIS researches in order to achieve ideal ionization effects.
Although high selectivity factor can be achieved by quasimonochromatic lasers, ionization yield is limited by the laser power.When high-power non-monochromatic laser is adopted in LIS, laser bandwidth plays an important role in selective photoionization process. Given this perspective, the semiclassical density matrix equations are adopted for conciseness and accuracy. In density matrix equations, atoms and monochromatic laser fields are controlled by the Schr¨odinger equation and Maxwell equations respectively. Because laser bandwidth is absent in density matrix equations naturally,several bandwidth models have been proposed previously,including the chaotic field model, the de-correlation model, and the phase diffusion model. In the chaotic field model proposed by Zoller,[28,29]the non-monochromatic laser field is regarded as a stochastic process with stochastic electric amplitudes and phases,thus original density matrix equations are reduced into an infinite set of differential equations. The decorrelation model developed, by Agostiniet al.[30]and Dai and Lambropoulos[31]is both a chaotic description essentially,with only zero-order quantities contained mathematically.The introduced laser spectra in these two models are the Lorentzian profiles. However, it is assumed that there exist stochastic laser phase and stabilized laser intensity in the phase diffusion model. And the laser bandwidth term in this model is modified by laser detuning,thus the introduced laser spectrum can be adjusted by the cut-off factors.[32,33]Additionally,Choeet al.proposed another model, in which the photoionization process in non-monochromatic laser fields is regarded as the interaction between atoms and a series of phase-independent monochromatic components.[34]However, this model is excluded in subsequent numerical simulations since its availability is open to question.
In the present work, we focus on a hypothetical atomic three-step photoionization process in non-monochromatic laser fields. Based on the semi-classical theory, three laser bandwidth models mentioned above are introduced into the density matrix equations. First, the physical model of atomic photoionization is presented. Then, three bandwidth models are compared and the model closest to physical practice is selected and used for further simulations. Next, the influences of several laser parameters and atomic Doppler broadening on the photoionization process are simulated and discussed. Finally,some conclusions are given.
2. Theoretical description
2.1. Density matrix equations of photoionization process
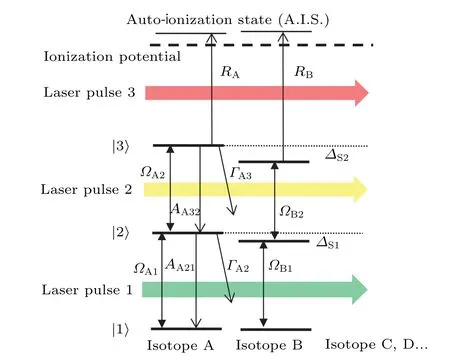
Fig.1. Schematic diagram of atomic three-step photoionization process.
It is assumed that there is an imaginary element with isotope A and isotope B, which are the target isotope and main‘harmful’ isotope of LIS respectively. As shown in Fig. 1,the excitation and ionization processes of a four-level atomic system with three laser pulses are taken into consideration.Three bound levels below the ionization potential are coupled by the first two laser pulses coherently, while the autoionization state and excited states are coupled by the third laser pulse incoherently. Generally,the auto-ionization rateRis introduced to substitute for the effect of the third laser because the transition to auto-ionization state involves multi-electrons excitation processes. Spontaneous decay of excited states is considered classically in density matrix equations.
Under the rotating-wave approximation (RWA), electric dipole approximation, and adiabatic approximation, the density matrix equations are written as
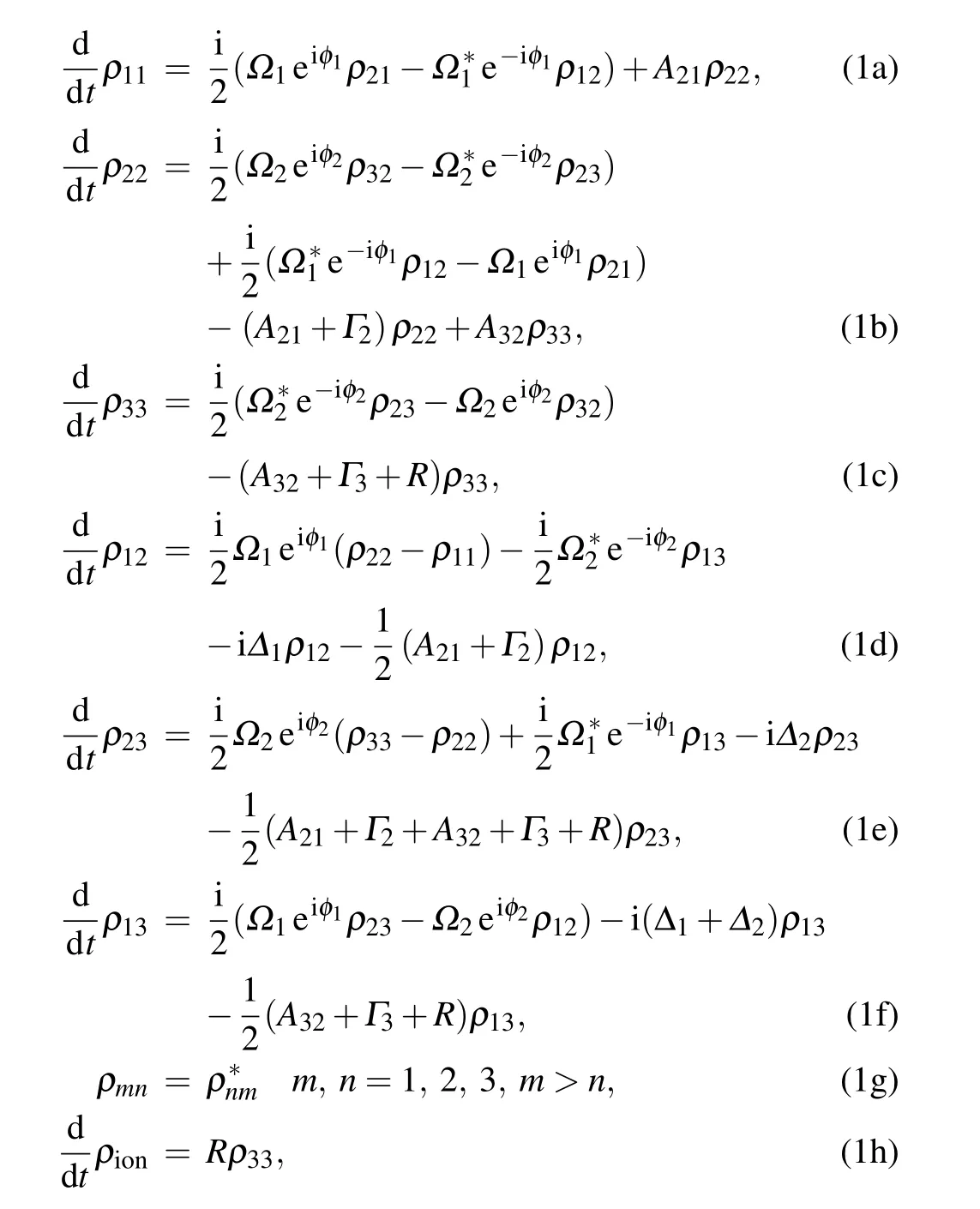
whereρmm(m=1,2,3),the diagonal element of density matrix,is the population probability of state|m〉;ρmn(m,n=1,2, 3,m/=n), the off-diagonal element, describes the degree of coherence between|m〉and|n〉;ρionis the ionization yield;φm(m=1, 2) is the phase of the electric component of laserm;Amn(m,n=1, 2, 3,m >n) andΓm(m=2, 3) indicate the spontaneous decay rate from|m〉to|n〉and to other lower states outside of this photoionization scheme, respectively;Ris the auto-ionization rate.Ωm(m=1,2)is the Rabi frequency and defined as

withEmbeing the electric field of laser pulse anddmthe atomic electric dipole moment for the transition from|m〉to|m+1〉,Δm(m=1, 2)is the frequency detuning and defined as

2.2. Introduction of laser bandwidth models
In the chaotic field model,it is assumed that the stochastic fluctuation of laser electric fieldE(t) obeys the Langevin equation. The stochastic process is described by its associated Fokker–Planck equation as follows:
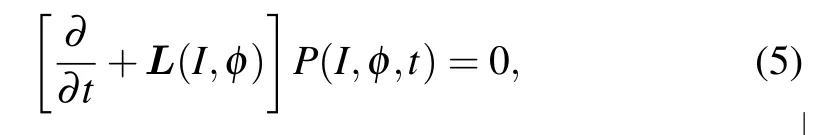
whereP(I,φ,t) is the distribution function of electric field with intensityIand phaseφat timetandL(I,φ) is the Fokker–Planck operator. With the help of Green’s functions, the stationary two timeα-order correlation functionG(α,α)(t,t′) of stochastic laser fields can be obtained as follows:
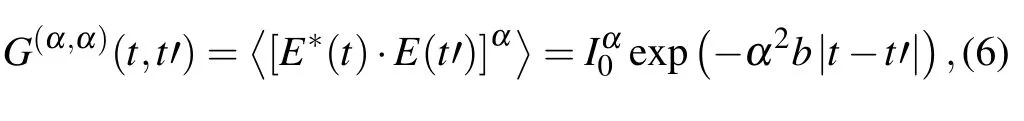
whereIandbis the mean intensity and bandwidth of laser field,respectively. The laser spectrum has a Lorentzian shape whenα=1.Under these circumstances,the atomic three-step photoionization process is too complex to solve numerically.Therefore,it is necessary to describe the stochastic process of laser by the Fokker–Planck equation,

By means of the statistical averaging method, the differential equations of density matrix elements are written as Eqs. (8)–(10). The detailed mathematical deductions can be obtained by referring to Refs.[28,29]and expressed below:
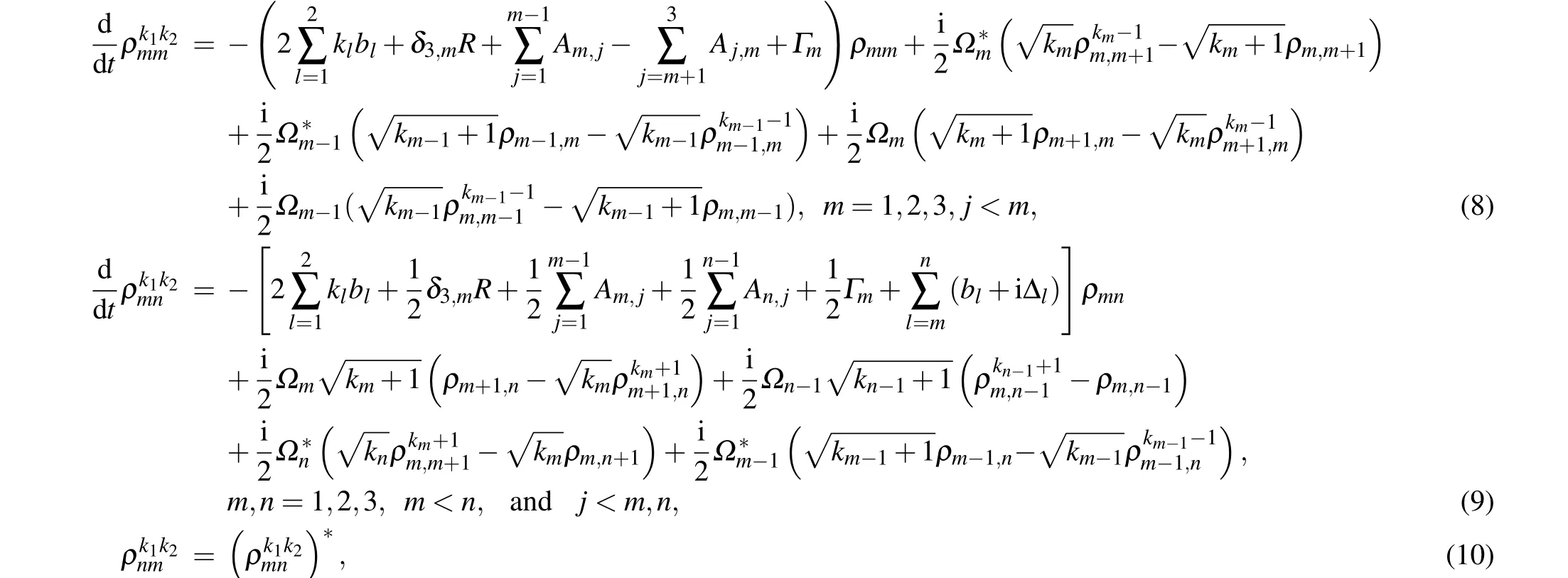

All of the atoms are supposed to populate the ground state initially. Therefore,the population rate att=0 ns can be written as
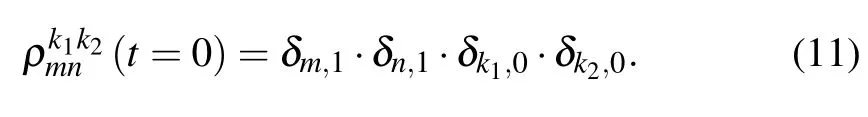
Although the simulation results converge gradually with the increase of laser correlation coefficient,the computational cost and memory consumption increase drastically at the same time. Hence,the finite correlation coefficients are adopted for convergence and accuracy in numerical simulations.
The de-correlation model is a simplified zero-order version of the chaotic field model essentially. Therefore,the differential equations of diagonal elements and off-diagonal elements are in the following forms:
The phase diffusion model can be considered as a modified de-correlation model mathematically. A modified bandwidth term,which includes the frequency detuningΔl(l=1,2) and cut-off factorsβl(l= 1, 2), replaces the previous one in the de-correlation model. The introduced laser spectrum is close to the Lorentzian profile whenΔl ≪βlbl, and reduces to the quasi-monochromatic form whenΔl ≫βlbl.The boundary between the non-monochromatic fields and the quasi-monochromatic fields is controlled by cut-off factorsβl.
3. Numerical simulation results
In this section, numerical simulations of atomic threestep photoionization processes are carried out. The four-order Runge–Kutta algorithm is adopted to solve the differential equations, and ionization yield of isotope A and selectivity factor of isotope A relative to isotope B are regarded as the judgment standards of the atomic three-step photoionization process with specific parameter values.
The simulation parameters are given as follows. Isotope shifts between isotopes A and B of two transitions are both 4.0 GHz. Lifetimes of the first and second excited states are 100 ns and 50 ns, respectively. Whereas systematic parameters are flexible,if one of them changes in a specific range,the remaining parameters are set to default values, unless otherwise stated. The Rabi frequenciesΩ1andΩ2and the autoionization rateRall have Gaussian profiles with 30-ns FWHM pulse width in the temporal domain. The peak values ofΩ1,Ω2, andRare 1.0 GHz, 1.0 GHz, and 0.2 GHz, respectively. The FWHM bandwidths of two excitation lasers are both 1.0 GHz for all bandwidth models. The atomic Doppler broadening is defaulted as 0. It should be noted that isotope shifts,atomic Doppler broadening,laser frequency detunings,and bandwidths are all expressed as angular frequencies.
In Subsection 3.1, three bandwidth models mentioned above are compared with each other. The effects of laser parameters on photoionization processes are simulated in Doppler-free manner in Subsections 3.2–3.5,and the effect of atomic Doppler broadening is included only in Subsection 3.6.
3.1. Comparison among bandwidth models
The population probabilities of two isotopes over the photoionization process are plotted in Fig. 2. The results in Figs.2(a)–2(d)are obtained in monochromatic fields,chaotic field model,de-correlation model,and phase diffusion model,respectively. The orders in the chaotic field model and cut-off factors in the phase diffusion model are set to be 2.0. The results of isotope A and isotope B are drawn by solid line and dotted line in the figures respectively. Some results of isotope B are enlarged in the figures because they are too minute to differentiate. As shown in Fig.2(a),the strong coherence is manifested for isotope A in monochromatic fields. The population probabilities present damped Rabi oscillations, and the ionization yield increases with a step-wise trend. Nevertheless,the population probabilities and ionization yield of isotope A vary smoothly over time in non-monochromatic laser fields,as shown in Figs.2(b)–2(d). Non-monochromatic laser fields can be regarded as the superposition of a series of monochromatic components intuitively. The evolutions of population probabilities are equivalent to the average value of Rabi oscillations with different oscillation frequencies,smoothing the single Rabi oscillation out. It should be noted that the results of isotope A in the de-correlation model and the phase diffusion model are identical because they have the same mathematical expressions in the resonant conditions, whereΔlof isotope A is equal to 0 in Eq.(15).
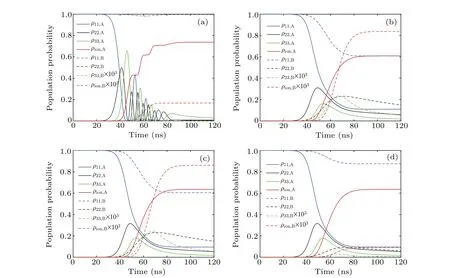
Fig. 2. Population probabilities versus time in (a) monochromatic fields, (b) chaotic field model, (c) de-correlation model, and (d) phase diffusion model.

Fig.3. Ionization yield of isotope A versus frequency detuning in several bandwidth models for(a)the first laser and(b)the second laser.
The photoionization process of isotope B presents a weaker coherence in monochromatic laser fields. The population probabilities and ionization yield display smooth variations because of non-resonant interactions. The results of isotope B obtained from the de-correlation model and the phase diffusion model are different becauseΔlof isotope B in Eq.(15)is not 0.
The ionization yield of isotope A in three bandwidth models is shown in Fig. 3, where the chaotic field model with several orders (0, 1, and 2), de-correlation model and phase diffusion model with several cut-off factors (1, 2, 5, and 20)are all displayed as a half of symmetrical curves. (i) The de-correlation model is equivalent to the zero-order chaotic field model and the phase diffusion model with infinite cutoff factors because of the same mathematical form. (ii) A lower ionization yield is obtained in the one-order chaotic field model than that in the zero-order model, whereas there are no distinguishable differences among the results of one-,two-, and even higher order model for mathematical convergence as shown in Fig. 3. Because the computational cost and memory consumption are proportional to the product of model orders, one- or two-order is enough in numerical simulations if chaotic field model is chosen. (iii) The spectral profile of isotope A’s ionization yield is close to Lorentzian profile in chaotic field model and de-correlation model. The introduced laser spectrum has a Lorentzian shape. The spectral power density(SPD)shows a relatively slow decline with the increase of frequency detuning. Accordingly, ionization yield presents similar characteristics. (iv)The spectral profile of isotope A’s ionization yield turns from a Lorentzian profile into a quasi-Gaussian profile gradually as the cut-off factorβldecreases from infinity in phase diffusion model. As mentioned in Subsection 2.2, the introduced laser spectrum manifests the Lorentzian profile for near resonance, and reduces into a quasi-monochromatic pulse for far off-resonance.Thus the profiles of SPD and ionization yield exhibit similar characteristics. The smaller the cut-off factor, the narrower the range of the Lorentzian profile is,thus ionization yield decreases with frequency detuning more rapidly for smaller cutoff factors.
The laser spectrum measured in experiment is closer to quasi-Gaussian profile, including the profile of ionization yield line shape.[14]Therefore, the phase diffusion model is adopted in following simulations and the cut-off factors of two lasers are set to be 2.
3.2. Rabi frequencies
The two-dimensional contours of ionization yield of isotope A (resonant isotope), isotope B (non-resonant isotope)and selectivity factor at various Rabi frequencies are shown in Figs. 4(a)–4(c), respectively, where the warmer color represents the higher value. Figure 4(d) shows the scatter diagram of ionization yield of isotope Aversusselectivity factor within the scope of simulations. Similar results are presented in Figs. 6, 7, 9, and 10 and they are not described to avoid repetition in the following subsections.
It is shown that the ionization yield of isotope A first rises rapidly and then declines slowly with the increasing of Rabi frequencies of two lasers. Larger Rabi frequency is needed to reach the maximum ionization yield for isotope B because of non-resonant excitation, that is, results in Fig. 4(b) can be regarded as a bigger version of the unsaturated excitation region in Fig. 4(a). Selectivity factor shows a monotonic decline trend, even on a larger scale as shown in Fig. 5. The blue (or red) line in Fig. 4(a) marks the position where ionization yield of isotope A reaches a maximum value under a certain Rabi frequency of laser 1 (or 2). It can be obtained from these two lines that the laser 1 has a lower saturated Rabi frequency than laser 2 naturally. Because the dipole moment of the first transition is generally bigger than that of the second one, much lower power density of laser 1 is required for saturation than laser 2. Besides, because near-saturation power density is adopted in general LIS experiments for effective utilization of resonant isotope, namely 1.0 GHz–3.0 GHz in Fig.4(a),the best result of optimization by adjusting Rabi frequency is to improve only one of ionization rate or selectivity,just as shown by the red line in Fig.4(d).
As shown in Fig.5,the ionization yield of isotope A first increases rapidly and then declines with one of Rabi frequencies increasing and another fixed. The decline is because of the AC Stark effect, whose detailed information is given in Subsection 3.4. The curve of the non-resonant isotope can be regarded as a translation and deformation of the resonant isotope’s curve. Accordingly, the selectivity factor displays a monotonic decline trend.
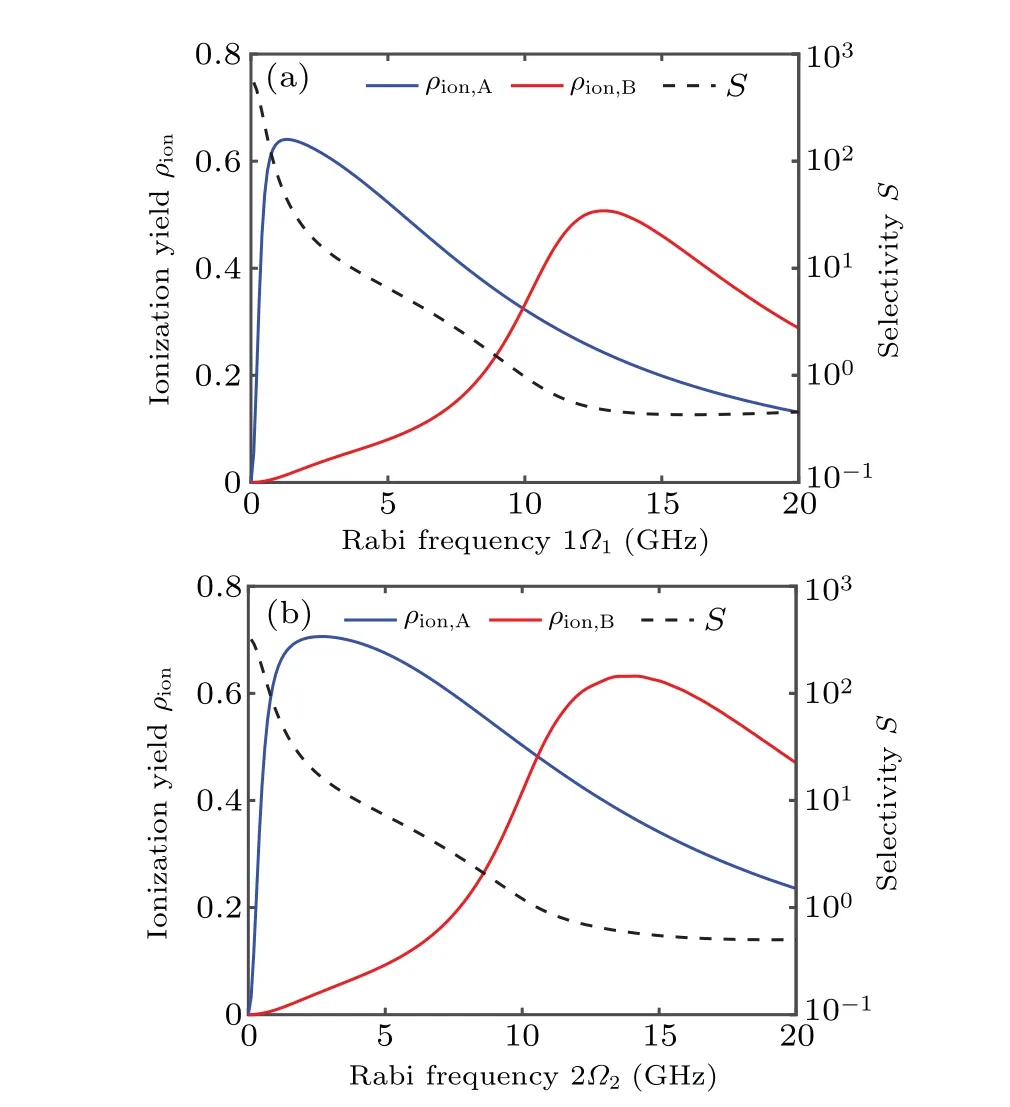
Fig. 5. Curves of ionization yield and selectivity factor versus Rabi frequency for the first laser and(b)the second laser.
3.3. Relative time delays
The influences of relative time delay between laser pulses are plotted in Fig. 6, where Δt12(or Δt13) indicates the time interval between peak Rabi frequencies of laser 1 and laser 2 (or laser 3), and the interval is assumed to be positive if laser 1 reaches atomic vapor earlier than others. The results of isotope A indicate that the maximum ionization yield is obtained under the near-synchronous condition, while selectivity factor has the contrary variation trend due to the fact that laser provides lower effective power density under the asynchronous condition. Because ionization yields of two isotopes decrease and selectivity factor increases in the unsaturated excitation process,the optimization result of relative time delay in Fig. 6(d) shows the similar properties to that in Fig. 4(d).Furthermore,because laser 1 interacts with atoms earlier than laser 2 and laser 3 in the three-step photoionization process,ionization yield displays a rapid decline if the former laser falls behind the latter.
3.4. Frequency detuning
The influences of frequency detuning on photoionization processes are plotted in Fig.7. In general,ionization yield decreases if any laser’s wavelength deviates from the transition’s central wavelength for any isotope.However,selectivity factor reaches its maximum value under a near-resonant condition as shown in Fig.7(c),which is in agreement with the experimental value qualitatively. Because of the two-photon resonance excitation from the ground state to the second excited state,the maximum value of ionization yield in non-resonant conditions appears whenΔ1+Δ2=0 and similar phenomenon can be observed in experiments.[36,37]It should be noted specially that the measurement of translation’s central wavelength deviates from its intrinsic value under the non-resonant excitation conditions,thus accuracy of laser frequency should be guaranteed in atomic spectrum scanning experiments.
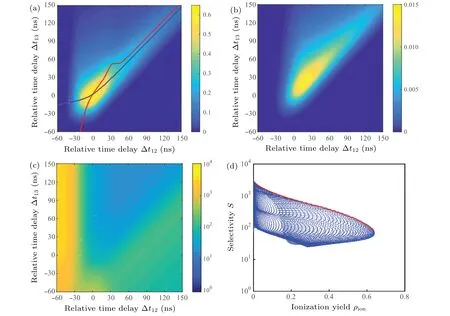
Fig.6. Influences of relative time delay on atomic three-step photoionization process,showing(a)ionization yield of isotope A,(b)ionization yield of isotope B,(c)selectivity factor,and(d)selectivity versus ionization yield.
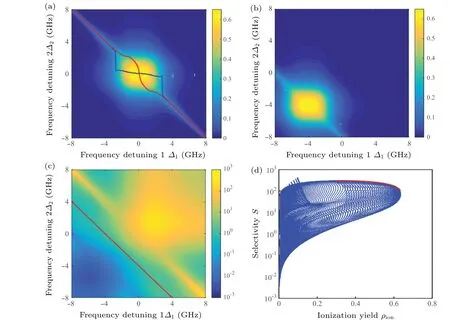
Fig.7. Influences of frequency detuning on atomic three-step photoionization process,showing(a)ionization yield of isotope A,(b)ionization yield of isotope B,(c)selectivity factor,and(d)selectivity versus ionization yield.
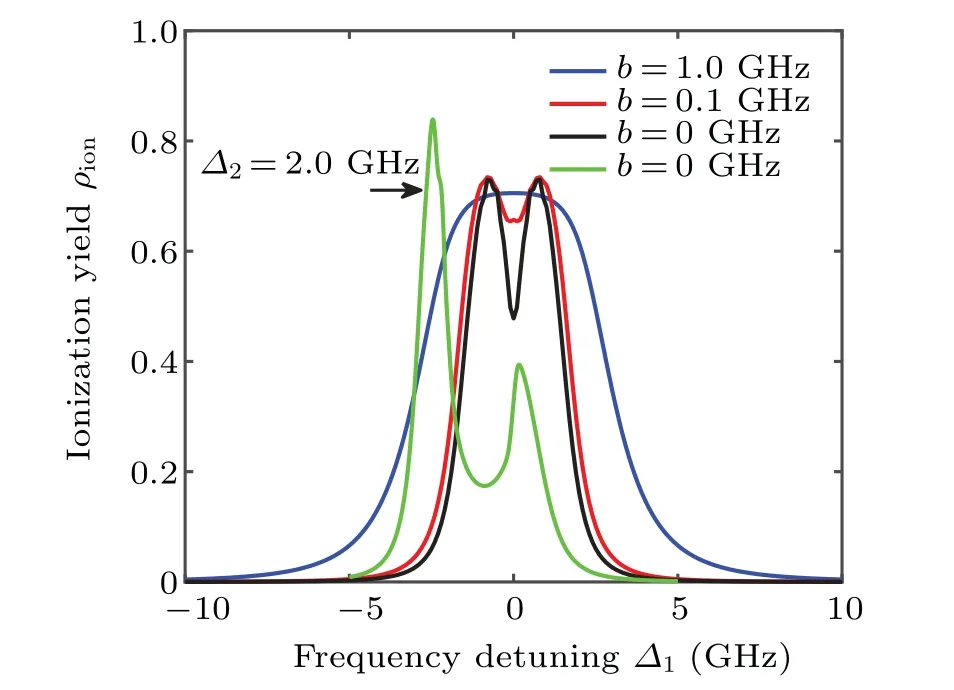
Fig. 8. Curves of ionization yield versus frequency detuning at several bandwidths, with corresponding Rabi frequencies: Ω1 = 1.0 GHz, and Ω2=3.0 GHz.
The ionization yield of isotope B can be obtained by translating the pattern of isotope A according to the isotope shifts because the atomic parameters of two isotopes are identical except for the resonant frequency. As a result,selectivity factors on both sides of red line in Fig.7(c)are reciprocals to each other. The distribution of scatters in Fig. 7(d) also indicates that improving ionization yield and selectivity factor simultaneously cannot be realized by tuning laser frequency.
It is widely known that the AC Stark splitting appears when Rabi frequency is larger than the decay rate of relevant state in coherent excitation, for exampleΩ1=1.0 GHz andΩ2=3.0 GHz in Fig. 8. The curves of ionization yieldversusfrequency detuning of laser 1 under resonant excitation are shown by the blue, red and black lines, respectively. The AC Stark splitting is gradually enhanced with laser bandwidth decreasing because of more significant coherent interactions between atoms and laser field. This effect even appears under non-resonant excitation and the splitting position moves towards the opposite direction of the laser 2’s frequency detuning as shown by the green line. The AC Stark splitting can be easily observed in spectrum scanning experiments.[38–40]
3.5. Laser bandwidths
Influences of laser bandwidths on photoionization processes of static atoms are plotted in Fig. 9. The ionization yield of isotope A displays a monotonic decline trend with the increase of each laser bandwidth. It can be seen that a lower Rabi frequency of laser 1 is required than that of laser 2 from the distribution of ionization yield in Fig. 9(a). Nevertheless, isotope B, the near-resonant isotope, requires nonmonochromatic laser fields to reach its maximum ionization yield, and the corresponding bandwidths are close to the isotope shifts as shown in Fig.9(b). That is because atomic ionization yield mainly depends on the SPD near to the translation’s central wavelength as simulated in Fig. 7. With the increase of laser bandwidth,the SPD near to translation’s central wavelength of isotope B first increases and then decreases,so does the ionization yield of near-resonant isotope.
Selectivity factor has similar variation properties to the ionization yield of isotope A, whereas it decreases violently near the zero-bandwidth region. Obviously, the ionization yield of isotope A and selectivity factor reach their maximum values under the circumstance of monochromatic laser fields. And the optimal results by adjusting laser bandwidths are shown in Fig.9(d),where the black line and red line mark the results when laser 1 and laser 2 are monochromatic fields respectively. It shows that laser 1 should have the priority of narrow bandwidth from the selective and efficient ionization standpoint. Furthermore, reducing laser bandwidth, or more specifically,compressing spectrum distribution, is a powerful and practical method of increasing selectivity factor of static atoms.
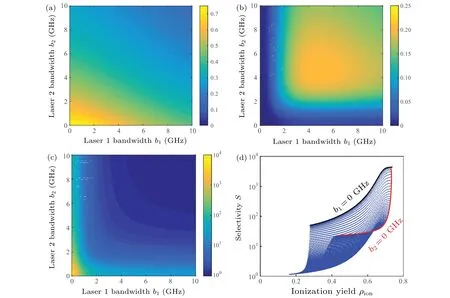
Fig. 9. Influences of laser bandwidth on atomic three-step photoionization process, showing (a) ionization yield of isotope A, (b) ionization yield of isotope B,(c)selectivity factor,and(d)selectivity versus ionization yield.
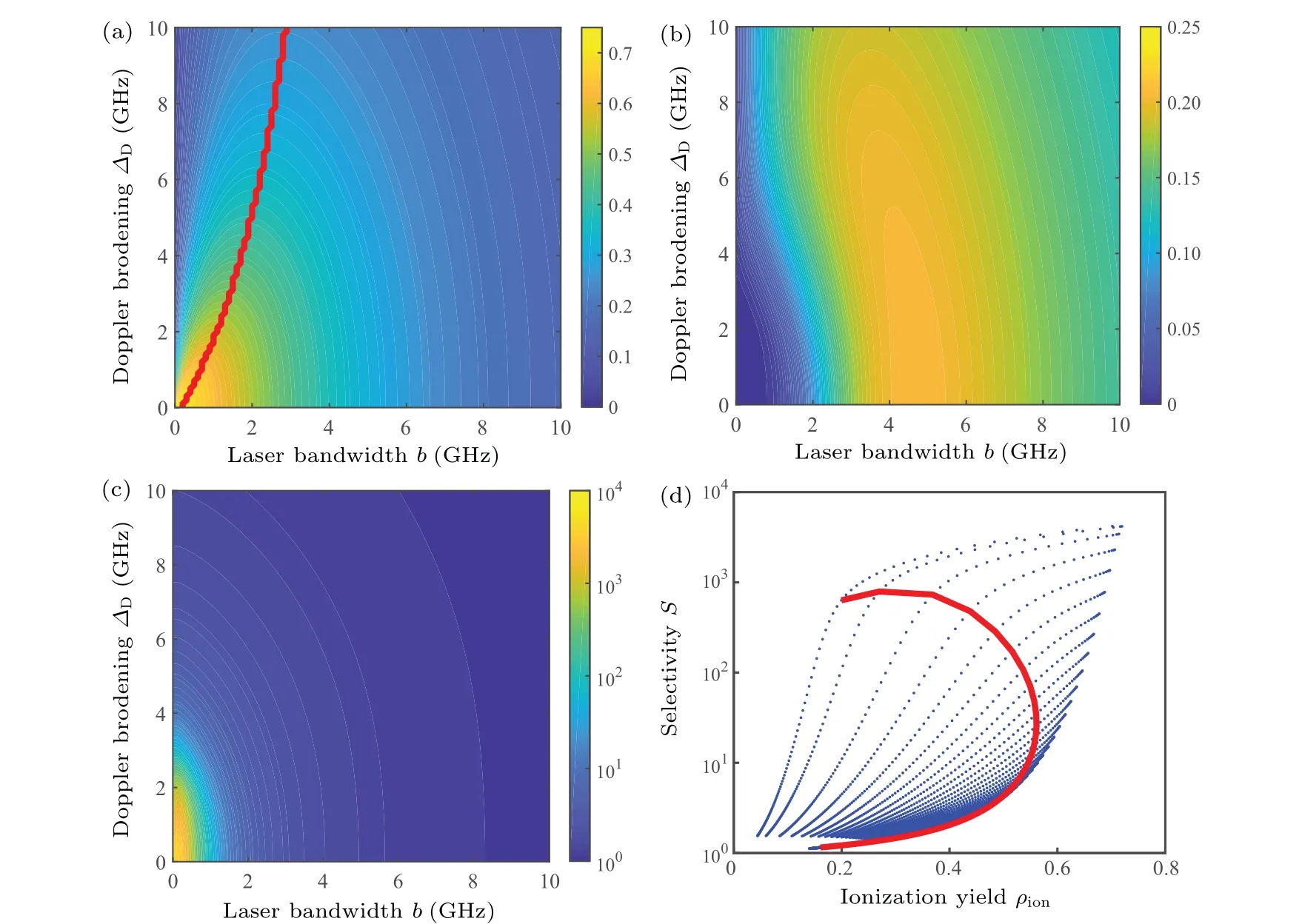
Fig.10.Influences of Doppler broadening on atomic three-step photoionization process,showing(a)ionization yield of isotope A,(b)ionization yield of isotope B,(c)selectivity factor,and(d)selectivity versus ionization yield.
3.6. Atomic Doppler broadening
As mentioned above,monochromatic laser fields are good choices for static atoms ionization in Doppler-free conditions.However,considerable Doppler broadening of atoms exists in a large-scale LIS process because of violent interatomic collisions and extended geometric demensions. The influences of the Doppler broadening and laser bandwidth are displayed in Fig. 10, where bandwidths of two lasers are set to be identical in simulations. The red line in Fig. 10(a) represents the position where the ionization yield of isotope A achieves the maximum value under some atomic Doppler broadening. It is concluded that non-monochromatic laser is appropriate for high ionization efficiency in a large scale LIS process and the bandwidth of laser is much less than atomic Doppler broadening. In addition, the more detailed simulations have been carried out in our previous work,[35]from which it can be obtained that the optimal bandwidth of laser 2 is smaller than that of laser 1 in Doppler-broadened photoionization processes because atoms populated at the first excited state have narrower broadening than those at the ground state.
Laser bandwidth has a similar effect on isotope B to that of Doppler broadening. Approximatively,the Doppler broadening leads the ionization yield to monotonically decrease.Generally,the ionization yield distribution of isotope B can be regarded as a translation and deformation of isotope A’s result.Consequently,selectivity factor has a strict decrease from the Doppler-free and zero-bandwidth point. Besides, the red line in Fig. 10(d) shows the relationship between ionization yield and selectivity factor with Doppler broadening of 2.0 GHz.The result indicates that the ionization yield and the selectivity factor can be not enhanced simultaneously by adjusting laser bandwidths under the Doppler-broadened conditions.
4. Conclusions
The atomic three-step photoionization process in nonmonochromatic laser fields is studied numerically for efficient selective photoionization in this article. Firstly, three typical laser bandwidth models are introduced into density matrix equations for comparison, and the phase diffusion model is employed in the subsequent simulations for correspondence degree to actual laser spectra. Then the influences of several critical laser parameters and atomic Doppler broadening on ionization yield and selectivity factor are discussed. The simulation results show that the ionization yield and the selectivity factor can be not enhanced simultaneously by adjusting Rabi frequency, relative time delay or frequency detuning individually. Monochromatic laser fields are necessary for high ionization efficiency and selectivity when Doppler broadening is negligible, such as spectrum scanning experiments.However, the bandwidth is not so narrower as that under the Doppler-broadened conditions from the high ionization efficiency standpoint. There is a trade-off between ionization yield and selectivity factor, and the interactions among various systematic parameters must be taken into consideration in optimization.
——福州市冯宅中心小学简介(二)
——福州市冯宅中心小学简介(一)
- Chinese Physics B的其它文章
- Switchable terahertz polarization converter based on VO2 metamaterial
- Data-driven parity-time-symmetric vector rogue wave solutions of multi-component nonlinear Schr¨odinger equation
- Neutron activation cross section data library
- Multi-phase field simulation of competitive grain growth for directional solidification
- A novel similarity measure for mining missing links in long-path networks
- Effects of electrical stress on the characteristics and defect behaviors in GaN-based near-ultraviolet light emitting diodes