Multi-phase field simulation of competitive grain growth for directional solidification

Chang-Sheng Zhu(朱昶胜) Zi-Hao Gao(高梓豪) Peng Lei(雷鹏)Li Feng(冯力) and Bo-Rui Zhao(赵博睿)

1College of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China

2State Key Laboratory of Gansu Advanced Processing and Recycling of Non-Ferrous Metal,Lanzhou University of Technology,Lanzhou 730050,China

3Network&Information Center,Lanzhou University of Technology,Lanzhou 730050,China

Keywords: multi-phase field model,directional solidification,grain competition growth,grain boundary orientation

1. Introduction

With the development of computer science, numerical simulation of the microstructure formed during the solidification of materials has become an important method of studying materials. The phase-field method is a powerful tool developed in recent years to study the microstructure evolution process. A large number of phase-field simulations have been carried out for the tissue evolution process in the directional solidification process, and a series of research results has been achieved to explain the law and the mechanism of evolution of tissue morphology.[1,2]Zhuet al. investigated the growth kinetics of dendrites with the specified growth direction,i.e., the vertical direction, and the morphological transformation during directional solidification by the phasefield method, and analyzed the effects of perturbation and anisotropic strength on the solidification organization,as well as the growth mechanism of the interfacial morphology and the transformation mechanism of the seaweed organization during the directional solidification.[3]Sakaneetet al. investigated the three-dimensional morphology of tilted equiaxed crystal growth in Al–Cu alloy under forced convection condition using the phase-field-lattice Boltzmann method, and the simulation results showed that the angle between the actual growth direction and the preferred growth direction indicated a significant variation with the angle between the preferred growth direction and the upstream growth direction.[4]Among the traditional research methods, it is of great scientific and engineering significance to study the crystal evolution of alloy directional solidification in depth, in which the dendrite competition due to the instability of grain boundary morphology is a key link to reveal the grain boundary evolution and dendrite elimination. For directional solidification converging bi-crystal competition growth, Walton and Chalmers described the competitive growth process between dendrites of different orientations based on the analysis of the relative position of the dendrite tips and the tip sub-cooling, and concluded that the preferentially oriented dendrites must eliminate the unfavorably oriented dendrites.[5]Esaka[6]and Rappaz and Gandin[7]expounded the main mechanism of competitive grain growth during directional solidification by studying the grain evolution structure of thin film samples in transparent alloy experiment, further summarized and graphically explained the research of Walton and Chalmers, and put forward Walton–Chalmers theory.D’Souzaet al.investigated the competition between the electively oriented dendrite dendrites and the unfavorably oriented dendrites in the CMSX4 nickelbased high temperature alloy and showed that the unfavorably oriented dendrites are eliminated when they are close to the favorably oriented dendrites and the secondary arm growth of the favorably oriented dendrites was also inhibited by the unfavorably oriented dendrites and the grain boundary direction remained parallel to the heat flow direction, a result that also confirms the Walton–Chalmers classical theory.[8]In recent years, with the in-depth study of the problem of grain competition in directional solidification,some scholars have questioned the Walton–Chalmers theory. Zhouet al.[9]suggested a convergent competition growth model in contrast to that raised by Walton–Chalmers when studying the experimental convergent growth of nickel-based high-temperature alloy IN792 and CMSX4 bi-crystals by the seed crystal method, and the results showed that under low pulling speed conditions, unfavorably oriented dendrites can also block the growth of favorably oriented dendrites, making favorably oriented dendrites obsolete. Liet al. conducted a quantitative simulation study of the convergent competitive growth process based on the phase-field simulation. The reasons for the abnormal elimination phenomenon were explained by analyzing the factors affecting the dendritic competitive growth, such as primary dendrite spacing and pulling speed.[10]Yuet al.performedin situobservations in a transparent alloy of SCN-2-wt%Ace,and the same anomalous elimination was found.[11]For the competitive growth of directionally solidified diverging bi-crystal,the evolutionary mechanism plays a role mainly through the secondary dendritic arms generated by the grains at the grain boundaries and the nascent spindles developed from the tertiary dendritic arms. Rappaz and Gandin[7]experimentally pointed out that during the growth of directionally solidified divergent bi-crystals, the favorably oriented dendrites generate secondary dendritic arms at the grain boundaries and then develop into new primary dendritic arms, the grain boundaries are continuously shifted toward the unfavorably oriented dendrites, and eventually the unfavorably oriented dendrites are eliminated, which is consistent with the classical Walton–Chalmers model regarding the phenomenon of divergent bi-crystal competition. However, Zhaoet al.[12]found the opposite phenomenon in an experiment on DD407 nickel-based high-temperature alloy directional solidification,indicating that when the favorably oriented dendrites and unfavorably oriented dendrites are biased in the same direction,there exists an angle between the favorably oriented dendrites and the heat flow direction, the favorably oriented dendrites eliminate the unfavorably oriented dendrites;when the growth direction of the favorably oriented dendrites and the unfavorably oriented dendrites deviate from each other and both deviate from the heat flow direction, usually the unfavorably oriented dendrites eliminate the favorably oriented dendrites. In recent years, there have been continuous in-depth studies of the competitive growth of directionally solidified dendrites,and Zhaoet al. studied the effect of tilt angle on the growth of tilted dendrites in Al–Zn alloys, and the simulation results showed that with the increase of tilt angle, the phenomenon of competitive growth among dendrites occurs.[13]Huiet al.used a binary alloy oriented multiphase field model to investigate the growth competition between columnar dendrites and degenerate algae during oriented solidification.[14]It can be seen that there are no consistent results for the study of the competitive growth of directionally solidified bi-crystals, and differences in the studied object and studied parameters may have large effects on the experimental results or even completely opposite results, so it is particularly important to systematically quantify the studied material. To address the problems of the current study,in this work,we take the SCN-0.24-wt% camphor model alloy as the research object and investigate the morphological evolution behavior of the competing growth processes of converging and diverging double grains between columnar dendrites of different angles in the directional solidification process by the phase-field method, and quantitatively analyze the effects of different crystal orientations,thermal gradient and pulling speeds on the evolution of grain boundary organization.

2. Mathematical model

2.1. Phase field equation and solute field eqnarray

The multi-phase field model arises from the need of simulating polycrystalline system. In a polycrystalline system,because different grains have different orientations,the difference in orientation cannot be described only by single phase field variable. In the multiphase model,multiple order parameters can be introduced to characterize multiple grains with different orientations. In order to better simulate the competitive growth and crystal boundary evolution of dendrites with different orientations in the directional solidification process,In this study,we adopt the quantitative multi-order parameter phase field model of dilute binary alloys developed by Ofori–Opoku and Provatas,[15]where a continuous variable ordered parameterφivarying from-1 to 1 is introduced to define each graini(1≤i ≤N,Nis the total number of grains),thus forming a phase field parameterφ=(φ1,φ2,φ3,...φN), whereφiwith 1 represents a large number of solids in thei-th grain andφiwith-1 refers to a large number of liquids or solids in the other grains. A well-characterized SCN-0.24-wt% camphor model alloy[16]is used as the object of study on the assumption that solute diffusion in the solid phase is neglected, and the temperature is replaced by using the approximation of the condensation temperatureT=Tref+G(x-VPt)whereTrefis the reference temperature and the position above the solidification axis is denoted byx. The interface energy anisotropy is expressed as the following equation:

2.2. Numerical simulation and physical parameters

In this work, we explore the explicit finite difference method on a uniform grid to discretize the multiphase field model,and in the time discretization an explicit first-order forward Euler equation is used to solve phase field equation and solute field equation,and in the Laplace operator a nine-point scheme is used to reduce the effect of grid anisotropy.The grid spacing is set to be Δx=0.8W0and the time step is assumed to be Δt=0.002τ0. To ensure the adequate growth of dendrites and the convergence of results, the computational domain is set to be 1500 μm×2600 μm and the simulation starts from two spherical seeds at the wall of the numerical domain.No-flux(or reflection)boundary conditions are applied to the domain boundary, and a sufficiently small diffusion interface thicknessξ=W0/d0is chosen to obtain accurate results.

In order to facilitate the calculation,the governing equation needs to be nondimensionlized,and in Eqs.(2)and(3)W0is used spatially andτ0temporall for dimensionless processing.τ0=a1a2W30/(d0Dl),wherea1anda2are taken from the results derived by Karma and Rappel for the asymptotic analysis of thin interfaces,[17–19]a1=0.8839 anda2=0.6762. It has been confirmed that a value of the dimensionless interface widthξ=38–54 is small enough to obtain quantitative results in numerical simulation,W0=ξ·d0. The pulling velocity isVP=R/G,and the dimensionless expression is ˜VP=VPτ0/W0.The thermal length islt=|ml|c0(1-k)/G, and the dimensionless expression is ˜lt=lt/W0. Assuming that the solute in the initial liquid phase is uniformly distributed,average solute concentration isc0,the physical parameters and other calculation parameters of SCN-0.24-wt%camphor model alloy used in the simulation are shown in Table 1.[16]

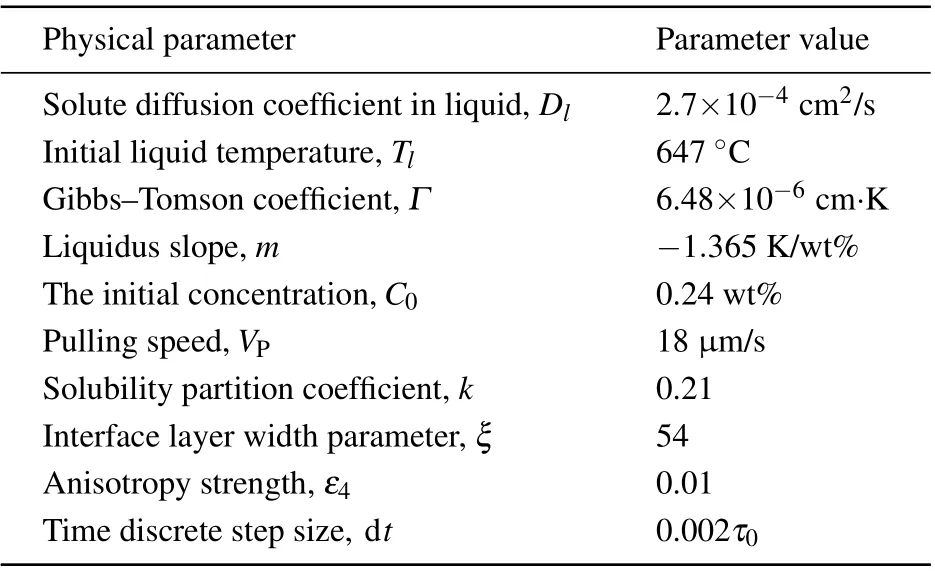
Physical parameter Parameter value Solute diffusion coefficient in liquid,Dl 2.7×10-4 cm2/s Initial liquid temperature,Tl 647 °C Gibbs–Tomson coefficient,Γ 6.48×10-6 cm·K Liquidus slope,m -1.365 K/wt%The initial concentration,C0 0.24 wt%Pulling speed,VP 18 μm/s Solubility partition coefficient,k 0.21 Interface layer width parameter,ξ 54 Anisotropy strength,ε4 0.01 Time discrete step size, dt 0.002τ0

3. Results and discussion

3.1. Analysis of convergent competitive growth process of bi-crystals

In the directional solidification convergent bi-crystal configuration and the divergent bi-crystal configuration, the dendrite with a small angle of deviation from the heat flow direction is favorably oriented dendrite, and the dendrite with a large angle of deviation from the heat flow direction is unfavorably oriented dendrite. The favorable tilt angle and unfavorable tilt angle are denoted by the symbolΘF0andΘU0,respectively,and are defined to be positive when the deflection direction is clockwise and negative when the deflection direction is counterclockwise. The process of elimination of directionally solidified grains is closely related to the tilted growth of dendrites. The classical Walton–Chalmers theory suggests that during the convergent growth of bi-crystals,the favorably oriented dendrites whose growth direction is closer to the heat flow direction will inevitably eliminate the unfavorably oriented dendrites whose growth direction deviates significantly from the heat flow direction. However, some experimental and simulation studies in recent years have demonstrated that the convergent growth of bi-crystals may undergo a paradoxical elimination phenomenon of unfavorably oriented dendrite elimination of favorably oriented dendrites under some conditions.[20–22]In order to study the analysis of the effect of changing only the tilt angle of unfavorably oriented grains on the competition of converging bi-crystals under all other conditions, the pulling speed and temperature gradient are fixed asVp=18 μm/s andG=0.001 K/μm, respectively, and the growth angleΘF0is set to be 0,i.e.ΘF0=0 for the favorably oriented grains along the heat flow direction,and the inclined growth angleθU0of unfavorably oriented grains is taken separately as-5°,-10°,-20°,-30°. Figure 1 shows the microstructures of convergent bi-crystals corresponding to different tendency angles(ΘU0=-5°,ΘU0=-10°,ΘU0=-20°,ΘU0=-30°)set for unfavorably oriented dendrites, the blue dendrites are the dendrites of favorably oriented grains, and the red parts are the dendrites of unfavorably oriented grains.As can be seen from Fig. 1(c), whenΘU0=-10°andt=5×104Δt,the dendrite b1 of the unfavorably oriented grain b gradually approaches to the dendrite a1 of the favorably oriented grain a. The elimination phenomenon occurs, and the dendrite b1 continues to grow after having been blocked by a1. The trunk of the a1 dendrite at the white dashed circle has a significant bend,which is caused by the interaction between the solutes of the two dendrites. When the tip of the unfavorably oriented dendrite b2 meets the tip of the favorably oriented dendrite a1, b2 is also blocked from growth, while the growth of the favorably oriented dendrite a1 is not affected,and similarly the unfavorably oriented dendrite b3 is eliminated when it meets the favorably oriented dendrite a1. It can be seen that whenΘU0=-10°, the competitive growth between the converging bi-crystals is consistent with the classical Walton–Chalmers model phenomenon, where the contact between favorably oriented dendrites and unfavorably oriented dendrites results in the elimination of the latter by the former,but the two grains do not eliminate each other and coexist for a long time. Figure 2 shows the structures and mophologies of the grain boundary whenΘU0=-10°, calculation time ist=1.4×105Δtandt=1.5×105Δt, respectively. From Fig.2(b),it can be seen that when the time ist=1.4×105Δt,the tip of b3 dendrite does not meet with a1 dendrite, the tip position of a1 dendrite and the tip position of a2 dendrite basically remain the same, and the solute interaction between the two dendrites is weaker. With the increase of the calculation step, when the time ist=1.5×105Δt, it can be seen from Fig.2(c)that the unfavorably oriented dendrite b3 meets with the favorably oriented dendrite a1 and the dendrite b3 is blocked from growing, but the tip position of the a1 dendrite and the tip position of the a2 dendrite remain basically unchanged, and the solute interaction between them remains weak. This indicates that as the unfavorably oriented dendrite b3 approaches to the favorably oriented dendrite a1 until it is eliminated, the whole process does not affect the growth of the favorably oriented dendrite a1,i.e.the solute interaction between both is too small to affect the growth of the favorably oriented dendrite. WhenΘU0is-20°and-30°, separately,it can be seen from Figs. 1(a) and 1(b) that unfavorably oriented dendrites are eliminated when unfavorably oriented dendrites meet with favorably oriented dendrites at both angles,and there is no effect on the growth of favorably oriented dendrites, which is consistent with the elimination phenomenon occurring atΘU0=-10°. During the evolution of the directional solidification bi-crystal convergence, with the increasing orientation angle of the unfavorably oriented dendrites,as shown by the yellow dashed circles in Fig. 1, the open area between unfavorable dendrites and computation area boundary is also increasing. The unfavorably oriented dendrites will generate the developed secondary dendrite arms in space,and then develop into tertiary dendrite arms to occupy the open area.

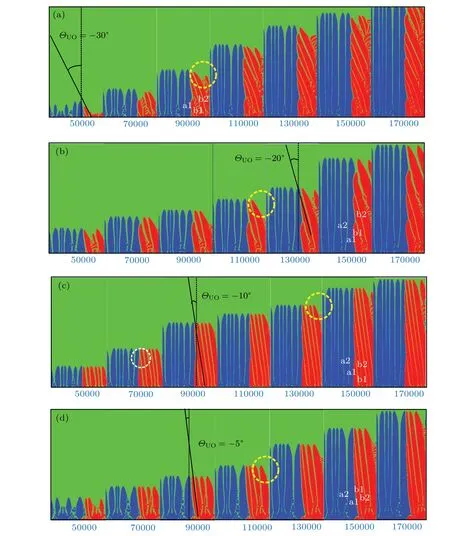
Figure 3 shows the relationship between the frequency of new tertiary dendrite arms of unfavorably oriented dendrites and the growth orientation angle of unfavorably oriented dendrites. It can be seen that theγvalue of unfavorably oriented grains gradually increases with the increase ofΘU0,i.e., the cubic dendrite arms are more easily formed in the open space between the non-preferred dendrite and the boundary of the computational domain.

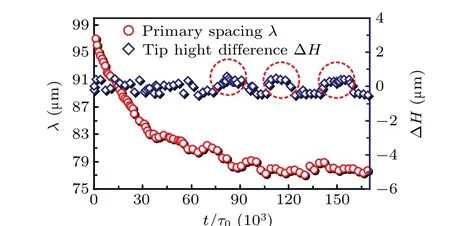
In order to quantitatively describe the elimination process of unfavorably oriented dendrites by favorably oriented dendrites,figures 4–6 show the evolution law of the primary arm spacingλand tip height difference ΔHbetween the favorably oriented dendrite a1 at the grain boundary and its adjacent favorably oriented dendrite a2 whenΘU0is-10°,-20°, and-30°, separately. It can be observed that the primary arm spacingλdecreases with time going by. This is because the solute field at the tip of the favorably dendrite a1 is affected by the solute field at the tip of the adjacent favorably dendrite a2. When it is reduced to the corresponding value,it will oscillate around this fixed value and remain basically constant.The tip height difference ΔHbetween the favorably dendrite a1 and a2 is relatively large at the beginning of a period of time. The tip height of a2 dendrite is obviously lower than that of a1 dendrite. At aboutt=5×104Δt,the tip height difference ΔHremains around 0. This is due to the fact that the grain boundaries are not stable when the dendrites first start to grow, and when the time reaches aboutt=5×104Δt, the dendrite interface reaches a basically stable state. As can be seen from Fig.6,whenΘU0=-3°,the calculated step size is aboutt=5×104Δtafter which the difference in height ΔHbetween the tips of favorably oriented dendrites a1 and a2 basically remains oscillating around 0,i.e.,the tips of dendrites a1 and a2 are basically at the same height. As can be seen from Fig. 5, the tip height difference between a1 and a2 atΘU0=-2°is basically the same as the state atΘU0=-3°,and also aftert=5×104Δt, the height difference ΔHfluctuates in a very small range around 0. Figure 4 shows the evolution of the primary arm spacingλand the tip height difference ΔHatΘU0=-1°. In general, the variation of the tip height difference ΔHfor the favorably oriented dendrites a1 and a2 is basically the same as that forΘU0of-30°and-20°, but it can be observed in Fig. 4 that the values of height difference ΔHin the three intervals marked by red dashed circles are all obviously positive,and the states of the corresponding dendrites in these three ranges are the states of the tips of unfavorably oriented dendrites b1,b2,and b3 near the favorably oriented dendrite a1 in Fig. 1(c), respectively. This is due to the fact that when the orientation angle of the unfavorably oriented dendrite is large, the tip height difference between the unfavorably oriented dendrite and the favorably oriented dendrite will be influenced by the subcooling, leading to a larger tip height difference,so the tip solute interaction between the unfavorably oriented dendrite and the favorably oriented dendrite is limited when the two are close to the favorably oriented dendrite.

On the contrary, when the orientation angle of the unfavorably oriented dendrite is small,the difference in subcooling between the unfavorably oriented dendrite and the favorably oriented dendrite is small,and the tip of the favorably oriented dendrite at the grain boundary is subjected to some growth restriction due to the interaction between the solutes at the tips of the two when the unfavorably oriented dendrite is close to the favorably oriented dendrite.

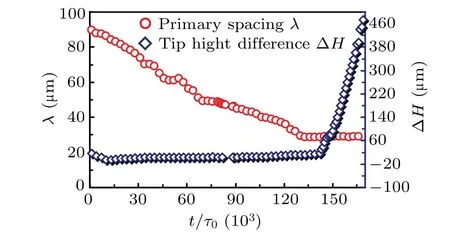
Figure 7 shows the time evolution of the primary arm spacingλand the tip height difference ΔHbetween the favorably oriented dendrite a1 and its neighboring unfavorably oriented dendrite b1 at the grain boundary atΘU0=-5°. It can be seen that the unfavorably oriented dendrite b1 gets closer to the favorably oriented dendrite a1 as time goes by,and the primary arm spacingλgradually decreases. When the time is aboutt=1.3×105Δt, the tip of the unfavorably oriented dendrite b1 touches the favorably oriented dendrite a1, the dendrite b1 blocke growing a1, and the primary arm spacingλalso tends to stabilize. Figure 8 shows the states of grain boundary evolution atΘU0=-5°att=1.3×105Δtandt=1.4×105Δt, respectively. From Fig. 8(b), it can be seen that when the time ist=1.3×105Δt, the solute interaction between the unfavorably oriented dendrite b1 and the favorably oriented dendrite a1 is weak,and at this time the dendrite b1 is not enough to influence the dendrite a1,and with the increase of the calculation time,the dendrite b1 is getting closer and closer to dendrite a1,as can be seen from Fig.8(c),when the time ist=1.4×105Δt,the interaction of solutes between dendrite b1 and dendrite a1 is strengthened, and the lateral solutes between the two cannot diffuse out, producing an enrichment of solutes, which affects the growth of dendrite a1.Figure 9 gives the tip concentration curves fort=1.3×105Δtandt=1.4×105Δt, respectively. It can be seen that as time passes, the slope of the tip concentration curve of dendrite a1 gradually becomes slower due to the proximity of dendrite b1,and the solute gradient decreases accordingly,resulting in a smaller growth drive of dendrite a1, which will affect the growth of dendrite a1. The growth of the favorably oriented dendrite a1 is affected, and the unfavorably oriented dendrite b2 has the potential to eliminate a1 to occur as a paradoxical elimination phenomenon.

When the drawing speed and temperature gradient are fixed atVp=18 μm/s andG=0.001 K/μm,respectively,and the values ofΘU0of unfavorably oriented grains are taken as-5°,-10°,-20°, and-30°, respectively, no anomalous elimination occurs in the simulation results, but the simulation results show that when the tilt angle is small, there may be the unfavorably oriented dendrites eliminating the favorably oriented dendrites. The reason for the absence of anomalous elimination in the simulation results may be that the given drawing speed is too large, the length of solute diffusion is relatively short,and the solute interaction between the dendrites is weak, which leads the unfavorably oriented dendrites to fail to eliminate the electrically oriented dendrites in a limited time. By reducing the original pulling speed toVp=4 μm/s, figure 10 shows the simulation results of converging bi-crystals when the orientation angle of unfavorably oriented dendrites is-10°. At this time, red grains are unfavorably oriented dendrites and blue grains are favorably oriented dendrites. It can be seen that as the unfavorably oriented dendrite b1 gradually approaches to the favorably oriented dendrite a1 at the grain boundary, the favorably oriented dendrite a1 is eliminated and anomalous elimination occurs, and as the grain boundary evolves, the unfavorably oriented dendrite b1 eliminates the favorably oriented dendrite a2 again. Yuet al. also observed the anomalous elimination occurring in the convergent competition growth process through the directional solidification in-situ experiment of transparent alloy SCN-2-wt%Ace.[11]The experimental results are shown in Fig. 11(a). The materials used in the simulations of this work and the materials used in the experiments of Yuet al.are transparent alloys,and the simulation results of this study are compared with the experimental results of Yuet al.in Fig.11 with a good fit. It can be seen that the occurrence of anomalous elimination phenomenon is greatly related to the pulling speed: the smaller the pulling speed,the stronger the interaction between the tip solute occurs,and the more likely to occur the anomalous elimination phenomenon is.

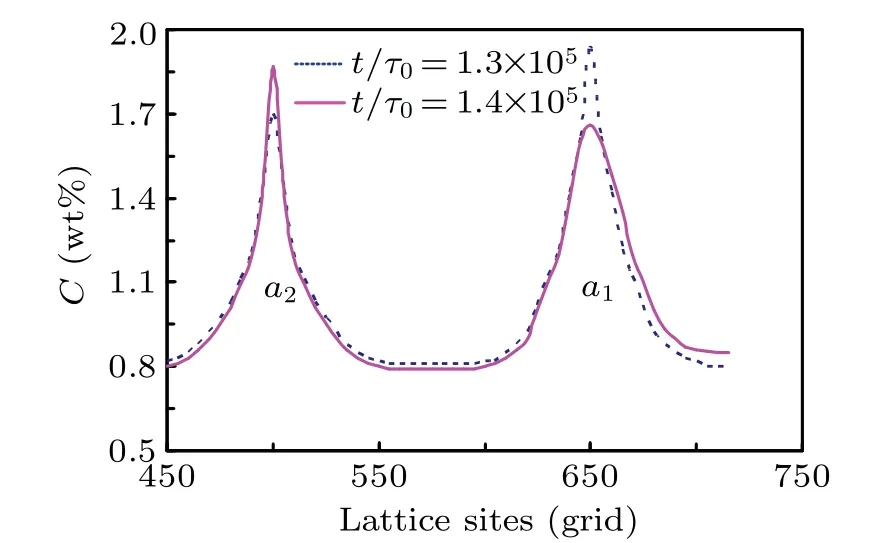
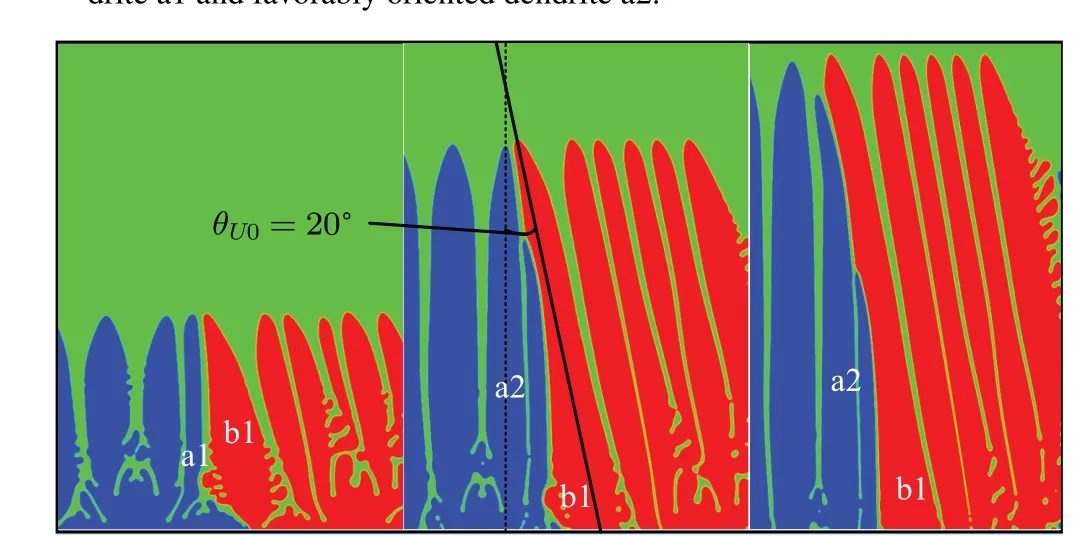
Figure 12 shows the interfacial morphologies of converging bi-crystals at three different angles with thermal gradients ofG= 0.00025 K/μm,G= 0.0005 K/μm, andG=0.001 K/μm, respectively. In the low thermal gradient state,such asG=0.00025 K/μm, the number of dendrites within the interface is less,the morphological levels of the dendrites at the two different angles are more distinct,and the dendrites have a strong branching capability, and more than three dendritic arms such as the same secondary dendritic arm appearing on the unfavorably oriented dendrites. In the high thermal gradient state, such asG=0.001 K/μm, the number of dendrites in the interface gradually increases and the branching capability of two different angles of dendrites decreases. It can be seen that the magnitude of the thermal gradientGis strongly related to the dendritic primary spacing. Dendritic primary spacing decreases with the increases of the thermal gradient, which is consistent with classic theory of primary spacing.[23]

3.2. Analysis of divergent competitive growth process of bi-crystals

Divergent growth refers to two sets of dendritic columns in which the favorable and unfavorable dendrites are far away from each other in the growth process,and the evolution process is mainly that the two grains in the growth process, the frontal grain boundary will continue to produce “V” open space, the two grains will be on the side towards the grain boundary so that the solute is fully diffused, and will not be affected by the other dendritic solute field. Both grains will be on the side towards the grain boundary to allow sufficient solute diffusion, and will not be affected by the solute field of other dendrites. Both favorable and unfavorable grains may generate secondary and tertiary arms at the diverging grain boundary and eventually develop into new primary arms to occupy the grain boundary space. The classical Walton–Charmers model suggests that during the directional solidification of the diverging bi-crystal,new secondary arms are formed at the grain boundaries of the favorably oriented dendrites and then develop into new primary dendritic spindles, with the grain boundaries advancing in the direction of the unfavorably oriented dendrites and eventually eliminating the unfavorably oriented dendrites.

The Walton–Charmers theory has been corroborated experimentally.[24–26]However,Wagneret al.[27]investigated the anomaly in experiment on CMSX4 high-temperature alloy diverging bi-crystal, where no new secondary dendrite arms appeared at the grain boundaries for the favorably oriented dendrites,and the grain boundaries were oriented in the same direction as the favorably oriented dendrites, and they concluded that the secondary dendrite arms formed by the unfavorably oriented had greater subcooling because the angle with respect to the heat flow direction was smaller than the favorably oriented secondary dendrite arms, so the unfavorably oriented dendrites were more likely to form secondary dendrite arms at the grain boundaries. This shows that the evolution of the grain boundary of the disperse bi-crystal in the directional solidification process has a certain randomness,and this randomness is essentially determined by the new primary arm generated by the grains in the middle of the disperse double crystal, and the new primary arm is developed by the tertiary dendritic arms,and the tertiary dendritic arms are derived from the developed lateral branching,so the randomness of the new primary arm is closely related to the developed lateral branching.

In order to study the effect of changing only the tilt angle of unfavorably oriented grains on the competition of diverging bi-crystals, with all other conditions being equal, the extraction speed and temperature gradient are set to beVp=18 μm/s andG=0.001 K/μm, respectively, and the growth of the favorably oriented grains in the direction of heat flow(ΘF0=0°)and the tilt angle of unfavorably oriented grains were set to beΘU0=10°,ΘU0=20°,ΘU0=30°, the blue part is for the dendrites of the favorably oriented grains and the red part is for the dendrites of the unfavorably oriented grains. As can be seen from Fig.13,the unfavorably oriented grains are tilted at angles of 10°and 20°, and new primary dendrite arms are generated at the black dashed circles for both the favorably oriented dendrites, and the yellow dashed line in the figure marks the direction of the grain boundary from the favorably oriented grains to the direction of the unfavorably oriented grains,which is inconsistent with the Walton–Charmers model nor with the anomaly found by Wagner,where both favorably and unfavorably oriented dendrites generate new primary dendrite spindles at the grain boundary. However, the developments of new primary arms from favorable dendrite in diverging grain boundary are still in the initial stage, the direction of grain boundary only slightly deflected,which cannot eliminate them. WhenΘU0=10°, the unfavorably oriented dendrite generates only one new primary dendrite arm in the grain boundary,and the time reachest=1.8×105Δt,the favorable newborn primary dendrite a1′with the unfavorably oriented newborn primary dendrite b1′at the grain boundary“V”where the undeveloped secondary dendrite arms grow slowly. WhenΘU0=20°, the secondary dendrite arms of unfavorably oriented dendrites at the grain boundary“V”are more developed and can form more stable primary dendrite arms. The above phenomenon is due to the fact that when the growth orientation of the unfavorably oriented dendrite is small, the space at the “V” formed by the favorably oriented dendrite and the unfavorably oriented dendrite is small,which is not conducive to the development of the secondary dendrite arms, and the angular difference between the secondary dendrite arms and the heat flow direction of the grain boundary is large, resulting in a smaller subcooling degree,and the secondary dendrite arms are not developed and do not easily develop into new primary dendrite arms. When the tilt angle of unfavorably oriented grains isΘU0=30°, the favorably oriented grains do not produce new primary dendrite arms,and the grain boundary direction is still along the growth direction of the favorably oriented grains;while the unfavorably oriented dendrites have more developed secondary dendrite arms due to the increase of the “V” shaped liquid-phase region at the grain boundary and the smaller angle between the secondary dendrite arm and the heat flow,which leads to the larger subcooling degree: the larger the orientation angle, the more easily the stable secondary dendrite arms in the region develops than the other two unfavorably oriented smaller dendrites. During the simulation of the growth of diverging bi-crystals at different angles,some of the tertiary dendrite arms generated on the developed lateral branches are eliminated due to the blockage of the surrounding dendrites as shown in Fig. 13(b), where the tertiary dendrite arms developed by the favorably oriented dendrites are eliminated due to the blockage of their own primary dendrite arms atΘU0=20°as shown by the yellow dashed circles. The yellow dashed circles in Fig. 14 indicate that atΘU0=28°, the tertiary dendrite arms developed by the unfavorably oriented dendrites are blocked and eliminated by the surrounding lateral branches, which shows that not all tertiary dendrite arms develop into nascent main axes during the growth of the diverging bi-crystal,and such tertiary dendrite arms are blocked with a random nature.

In order to understand more intuitively the growth pattern of divergent bi-crystals with different growth orientations of unfavorably oriented dendrites, the growth process of divergent bi-crystals is simulated when the tilt angle of unfavorably oriented dendritesΘU0is 22°and 28°, separately. As shown in Fig.14,whenΘU0=22°,compared withΘU0=2°no new primary dendrite arm appears in the favorably oriented dendrite a1. It can be seen that there is a correlation between a new primary dendrite arm appearing in the favorably oriented dendrite and the tilt angle of the unfavorably oriented dendrite during the growth of the diverging bi-crystal: as the tilt angle of the unfavorably oriented dendrite increases, the probability of developing a new primary dendrite arm in the favorably oriented dendrite becomes smaller.

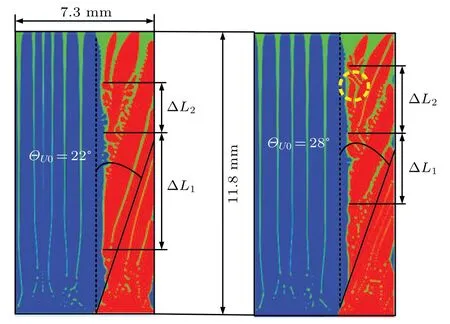
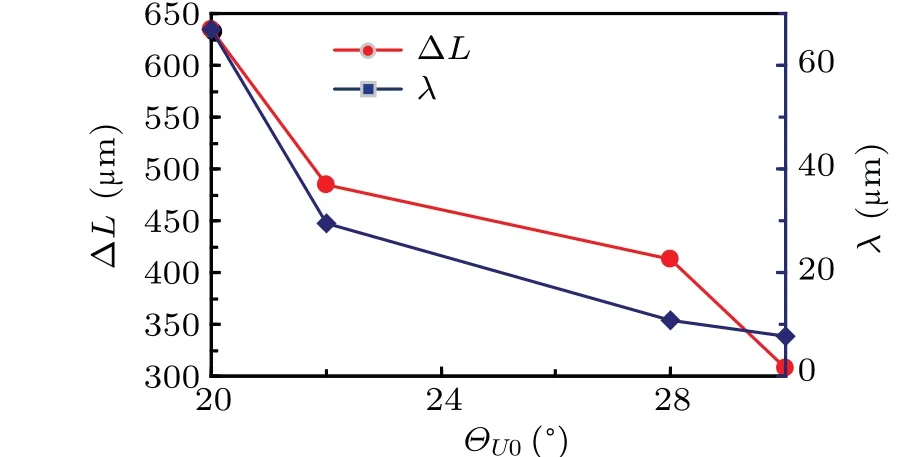
Figure 16 shows the relationship between the new spindle frequency and the growth orientation of unfavorable dendrites.It can be seen that the new spindle frequency of the favorably oriented grains is significantly higher than that of the unfavorably oriented grains whenΘU0is small at first, but with the increase ofΘU0, theγvalue of the favorably oriented grains shows monotonically decreasing, roughly atΘU0= 28°the new spindle frequency is 0. On the contrary,theγvalue of unfavorably oriented grains increases significantly,which shows that as the difference of bi-crystal growth direction becomes larger, the ability of favorably oriented grains to occupy the grain boundary space becomes smaller,and it is difficult to develop new primary dendritic arms to occupy the liquid phase grain boundary space, while the unfavorably oriented grains are more likely to generate new spindles, which further confirms the previous conclusion.

4. Conclusions

The competitive growth process between grains of different orientations in the directional solidification process is numerically simulated using the phase-field method.The branching behavior due to different grain boundary orientations of convergent and divergent bi-crystals and the growth pattern in the case of large-scale calculations are investigated and concluded as follows.

(i) In the process of convergent bi-crystal competition growth, the growth direction of favorably oriented dendrites is consistent with the direction of heat flow. When the pulling speed is too large,the orientation angle of the unfavorably oriented dendrites varying from small to large value is the normal elimination phenomenon of the favorably oriented dendrites blocking the unfavorably oriented dendrites: no anomalous elimination occurs and the grain boundary extends along the growth direction of the favorably oriented dendrites. When the pulling speed becomes small, the anomalous elimination phenomenon of unfavorably oriented dendrites eliminating favorably oriented dendrites occurs at the grain boundaries. The thermal gradient also has a great influence on the growth of dendrites. In the low thermal gradient state, the number of dendrites within the interface is less,the morphological levels of the dendrites at the two different angles are more distinct,and the dendrites have a strong branching capability,and more than three dendritic arms such as the same secondary dendritic arm will appear on the unfavorably oriented dendrites. In the high thermal gradient state,the number of dendrites in the interface gradually increases and the branching capability of two different angles of dendrites decreases. When the bi-crystal converges, the space is formed between the unfavorably oriented dendrites and computation area boundary. The unfavorably oriented dendrites will generate the secondary dendrite arms in this area, which then develop into tertiary dendrite arms to gradually occupy the space,and as the angle of unfavorable orientation increases, the more tertiary dendrite arms are produced by the unfavorably oriented dendrites.

(ii) During the competitive growth of the evanescent bicrystal,the growing direction of the favorable dendrites is consistent with the heat flow direction.When the orientation angle of the unfavorable grains is small,the frequency of spindle addition of the favorable grains is significantly higher than that of the unfavorable grains. As the orientation angle of unfavorable dendrites becomes larger, the unfavorable grains are more likely to develop stable secondary dendritic arms, and then the new primary dendritic arms occupy the liquid-phase grain boundary space,the grain boundary deviates from the favorable dendrites and tilts in the direction of unfavorable dendritic growth,but the grain boundary direction is still parallel to favorably oriented dendrites. In addition, the tertiary dendrite arms on the developed secondary dendrite arms may also be stopped by the surrounding lateral branches from further developing into nascent main axes, and this blocking of the tertiary dendrite arms has a stochastic nature, which in turn has an influence on the generation of primary dendrite arms in the grain boundaries.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 52161002, 51661020, and 11504149), the Postdoctoral Science Foundation of China(Grant No. 2014M560371), and the Funds for Distinguished Young Scientists of Lanzhou University of Technology,China(Grant No.J201304). The authors thank Dr. Xing Hui for his helpful discussion in code.