基于消隐点的线结构光传感器光平面标定方法*
胡 增,高兴宇,李伟明,尹炳强,于泽华
(桂林电子科技大学广西制造系统与先进制造技术重点实验室,桂林 541004)
0 引言
线结构光传感器具有非接触、速度快、精度高的优点[1-3],被广泛应用于三维测量和质量检测等方面。光平面标定是结合标定靶物的几何约束和摄像机透视原理,获取线结构光模型中光平面方程参数的过程[4],参数标定结果直接影响三维坐标计算精度。早期的光平面标定方法大多借助精密的辅助设备,如Dewar的拉丝法[5],徐光佑等[6]提出的基于交比不变性的三维靶标法,段发阶等[7]提出的锯齿靶标法等。徐与段的方法要求光平面垂直投射于标定块,人工调整困难,并不适合工程化应用。
线结构光的标定靶标可分为一维靶标、平面靶标和立体靶标。周富强等[8]采用一维射影变换的方法获取一维靶标上特征点的三维坐标,尤其适用于大尺寸结构光测量的标定,但是基于一维靶标的标定方法一次只能得到光平面中一个特征点,效率较低。LIU等[9]利用球形靶标成像后轮廓形状不受靶标位置影响的性质,采用空间球与椭圆锥面相交得到光平面方程。WANG等[1]利用线结构光与圆柱体交线沿轴线投影是标准圆的性质标定传感器参数。LIU和WANG采用的立体靶标标定方法采集一组靶标图像即可完成标定,不需要多次调整靶标的位姿,人工调整的工作量少,但是标定原理和图像处理方法相比一维靶标和平面靶标更复杂。
周富强等[10]提出了一种自由移动平面靶标的光平面标定方法,采用交比不变性原理提取不同位姿下棋盘格图像中特征点的局部坐标,然后利用摄像机的外参将特征点统一到世界坐标系并拟合光平面方程。自由移动平面靶标法已成为最主流的标定方式之一,不同方法之间的区别在于求解光平面中特征点或线的原理不同。韩建栋等[11]采用共线三点透视原理求解特征点三维坐标;魏一等[12]利用特征点图像坐标与相机光心确定的射线,然后与靶标平面相交计算特征点三维坐标;于龙龙等[13]利用摄像机外参通过坐标变换得到标定板不同位姿下与光平面交线的直线方程。PAN等[14]建立光平面坐标系到图像坐标系的单应性矩阵标定传感器参数,但要求靶标移动方向与光平面平行,调整较困难。WEI等[15]提出基于消隐原理的光平面标定方法,利用消隐点、消隐线与直线方向向量、平面法向量的关系,分两步标定得到光平面方程的参数。由于平行光条消隐点相同,该方法并不适用于平面靶标作一组平移运动的情形,为此陈天飞等[16]通过控制靶标作两组平移运动标定光平面法向。
基于消隐原理的标定方法不需要利用相机外参,避免了单应性矩阵分解的误差,具有较好的精度和鲁棒性。当前线结构光传感器与直线移动机构相结合的场景相当普遍,为解决传统基于消隐原理的标定方法不适用于标定板作一组平移运动的问题,进一步降低人工调整的工作量,提出一种基于平面靶标作一组平移运动的光平面标定方法。结果表明,本方法与几种传统的标定方法相比具有更高的标定精度。
1 基本原理
1.1 传感器数学模型
线结构光传感器的标定包含相机标定和光平面标定两部分,本文采用张正友标定法[17]标定相机的内参矩阵和畸变系数,记内参矩阵为K。
(1)
式中,fx、fy分别为X、Y轴方向的尺度因子;γ是倾斜因子;(u0,v0)为主点坐标。由相机的小孔成像模型可得:
s·[u,v,1]T=K·[x,y,z]T
(2)
式中,s为尺度因子;u、v为三维空间中某特征点在图像中去畸变后的像素坐标;x、y、z为该特征点在相机坐标系下的三维坐标。线激光器投射出的平面光束在相机坐标系下可描述为:
ax+by+cz+d=0
(3)
式中,(a,b,c)为光平面的法向量。在已知相机内参和光平面方程的条件下,可由光平面上特征点的像素坐标唯一确定该特征点在相机坐标系下的三维坐标值。
1.2 消隐点原理
基于消隐原理的光平面标定方法一般分为两步,第一步利用消隐的原理标定光平面的法向量,第二步利用光平面中已知三维坐标的特征点或几何约束求解参数d。在射影变换下,空间平行直线在图像中不再具有平行性,而是交于一点,该点称之为消隐点[3],且直线的方向向量与消隐点存在以下关系[15]:
D=K-1V
(4)

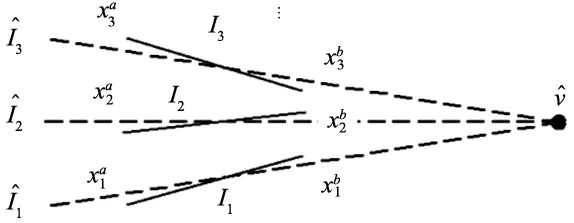
图1 消隐点最大似然估计
(5)

2 标定方法
2.1 法向量标定
平面靶标与光束平面的交线为一空间直线,如图2所示,激光条纹直线L1、L2同属于光束平面,且L1、L2分别属于经过平移后的标定板平面B1、B2。显然B1、B2相互平行,因此L1、L2不可能相交,由空间几何的结论可得L1、L2相互平行。同理可证明标定板平移运动下形成的一系列激光条纹构成了光平面中的一组平行直线段,记该直线段集合为SL。

图2 平面靶标平移运动模型
除线段集SL外,光平面中还可以构造出其他的平行线段集合。记Lij为第i次平移后的标定板上第j条沿标定板X轴方向的网格线,Lij与Lmn组成的平面记为LijLmn,光条直线Li与Lij的交点记为Pij。从图2可知,平面L11L21平行于平面L12L22,直线P11P21、P12P22同属于光平面,因此P11P21平行于P12P22,同理可证明P11P21、P12P22、P13P23、P14P24、P15P25、P16P26是光平面中一组平行直线段,记该线段集合为Sx。不同于集合SL,集合Sx中任一线段的像并不能从单张图像中直接提取得到。如线段P11P21在图像中的像,至少需要从两张平移运动的标定板图像中提取出两个交点的像素坐标才能确定。在标定板多次平移的情况下,线段的像可由一系列交点像素坐标拟合得到。通过平行线段集Sx的图像可确定光平面的一个消隐点,求解方法如下:
(1)记标定板平移运动下采集的投射有光条的标定板图像为ML,无光条的标定板图像记为MB,ML、MB中图像数目均为n,ML中的第i张光条图像记为MLi,同一位姿下的标定板图像记为MBi;
(2)从i=0开始,提取MLi的光条中心并拟合光条Li的直线方程。提取标定板图像MBi的角点坐标,拟合标定板局部坐标系X轴方向的直线方程,并求解该组直线与Li的交点坐标,依次存入二维数组AP的第i行,直到i=n。
(3)分别对二维数组AP每一列的像素点坐标拟合直线方程,计算该组直线被标定板首末位置截取的线段,如P11Pn1、P12Pn2等,按照最大似然法求该组线段的交点,该交点即为光平面中平行线段集Sx的消隐点。
由消隐的原理可得,只要得到光平面上两组平行直线的消隐点,即可确定光平面法向。因此,控制标定板或传感器作一组平移运动足以标定光平面法向。综上所述,本文光平面法向标定的流程如下:
(1)借助平移机构控制标定板作一组平移运动,采集投射有光条的标定板图像和同一位姿下不投射光条的标定板图像,分别为ML、MB;
(2)对ML组图像提取光条中心并拟合直线方程,求解平行光条线段的消隐点;
(3)求解平行线段集Sx的消隐点;
(4)利用式(4)求解两消隐点对应的方向向量,两方向向量的叉积即为光平面法向。
2.2 参数d标定
图3为标定板在初始位置的俯视图,L1为结构光条纹,标定板沿Y轴方向的网格线记为LY1i,其中i=1,2,…,dL为结构光条纹被标定板沿X轴方向网格线截取的线段长度。采用消隐原理可求出dL的实际尺寸,然后利用该约束条件可标定光平面方程中的参数d。

图3 标定板俯视图
拟合MB中所有标定板图像沿Y轴方向的直线方程,按照最大似然法求解所有Y轴方向平行直线的消隐点,由式(4)可得标定板局部坐标系Y轴的方向向量。记Y轴的方向向量为DY,光条直线方向向量为DL,图3中dL的实际尺寸为:
(6)
式中,db为标定板的方格尺寸,若已知两相邻特征点在相机坐标系下的三维坐标,可得:
(7)
式中,xi,j、yi,j和zi,j为特征点Pij在相机坐标下的三维坐标,联立式(1)~式(3)可得特征点的三维坐标为:

(8)
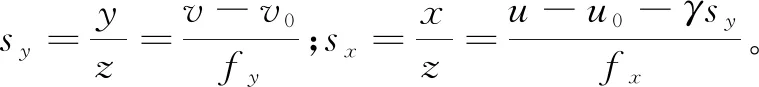

(9)

3 实验与结果分析
为验证本文方法的正确性,将视觉传感器安装在焊接机器人末端,传感器的相机型号为MV-EM500C,所采用的线激光投射器中心波长为650 nm,功率100 mW,线宽0.1 mm。控制传感器沿机器人基座标系Z轴作平移运动,保证标定板在相机视场范围内。分别采集了5组有激光条纹的图像和同一位姿下没有投射激光条纹的图像,图4为采集的一组图像样本。

(a) 标定板图像 (b) 光条图像
分别采用周富强等[10]所提算法、魏一等[12]所提算法、陈天飞等[16]所提算法与本文方法利用同一组图像对传感器参数进行标定,对于陈天飞所提算法另采集了一组平移运动下的光条图像,3种标定方法得到的光平面方程如表1所示。

表1 光平面标定结果
从表1可以看出,本文方法的标定结果与采用周富强和魏一所提算法的标定结果十分接近。为进一步验证本文标定方法的精度,分别采用表1中3种方法的标定结果,对一公称尺寸为7 mm的标准量块进行测量,图5为测量装置。

图5 结构光测量装置
控制传感器沿机器人基座标系X轴方向平移运动,同时控制相机采集结构光条纹图像,采用灰度重心法提取条纹中心,计算中心点三维坐标并生成点云,通过拟合两平面并计算两平面之间的距离得到量块高度的测量尺寸,图6为量块的光条图像和生成的点云,对量块测量10次的数据如表2所示。

(a) 量块光条图像 (b) 量块点云

表2 高度测量误差 (mm)
由表2可知,采用本文标定方法时,对厚度为7的标准量块的平均测量误差约为0.013,测量精度高于周、魏和陈所提方法。其原因一方面是由于基于消隐原理的光平面标定方法不存在单应性矩阵的分解误差,不需要将特征点三维坐标统一到世界坐标系,减少了误差来源。另一方面,本文采用最大似然估计方法对消隐点的定位精度高于陈所采用的最小距离平方法。由于相机景深的限制,实验时传感器作平移运动的范围较小,无法使光条布满整个图像,这也是导致本实验中陈所提算法测量误差较大的原因之一。
4 结论
本文提出了一种线结构光传感器标定方法,利用工业机器人控制传感器作一组平移运动实现光平面标定,该方法减少了标定过程中的人工参与,尤其适用于含平移机构的线结构光传感设备自动化标定。除平行的光条直线外,本方法利用标定板平移运动的特性,提取出光平面中另外一组平行直线,并利用两个消隐点标定光平面法向,解决了传统基于消隐原理的光平面标定方法不适用于标定板作一组平移运动的问题。与基于单应性矩阵分解的标定方法相比,本方法不存在外参分解误差,实验表明本方法标定精度更高,进一步验证了基于消隐点原理的标定方法的精度优势。

