基于Hammerstein模型的动态率相关迟滞特性建模及分析*
李 亮,喻 俊,温盛军
(中原工学院a.电子信息学院;b.彼得堡航空学院,郑州 450007)
0 引言
随着社会的进步和科技的发展,我国超精密机械加工制造业对分辨率、定位精度与响应速度提出了更高的要求[1]。以压电材料制作的压电驱动器具有微纳米级别位移精度、能耗低、响应速度快等优点[2],被广泛应用在超精密加工和微纳米定位技术等领域中。但在工业实践应用中,由于压电材料一直存在的迟滞非线性特性,会直接影响压电驱动定位平台的性能,降低控制精度,甚至导致系统的不稳定[3]。迟滞非线性具有明显的多值映射性[4],使平台非线性情况变得更复杂,对平台控制精度的影响最大。因此如何根据平台特性精确的建立其数学模型和对平台进行补偿控制已成为精密定位研究中的一个热点[5]。
迄今,为了精确描述压电定位平台的迟滞非线性特性,常用的模型主要是基于迟滞非线性现象建立的唯象模型,如PI(prandtl-shlinskii)模型[6]。该模型具有解析逆的优点,有利于控制方案的设计。然而,随着研究的逐渐深入,研究人员发现压电材料还具有动态的率相关特性,迟滞环会随着输入信号频率的增大而变宽,使得压电定位平台出现定位误差增大和振荡等问题[7]。前述的PI模型只能描述率无关的迟滞性质。为此,WONG等[8]利用在线支持向量机和相关向量机使其模型具有了率相关特性,但其设计过于复杂,不便于实现。JANAIDEH等[9]将输入信号变化率引入到PI模型的阈值内,提出了RDPI(rate-dependent prandtl-shlinskii)模型,但其并未考虑系统的机理动态特性。
针对压电定位平台在宽频域内存在的复杂输入-输出之间的动态率相关的迟滞非线性特性问题,本文提出了一种基于Hammerstein模型的动态率相关迟滞非线性建模方法,其中静态子系统部分使用经典PI模型进行描述,动态子系统部分使用率相关的二阶传递函数表征。为了更好地表征不同频率下的压电定位平台的性质,分别在低频和中高频的情况下建立了不同的传递函数模型。
1 压电定位平台系统建模
1.1 Hammerstein模型
Hammerstein模型是由各个子系统进行串联连接组合的一种非线性模型。一般情况下,其主要包含两个部分,第一部分是一个静态非线性子系统,其一般描述整个系统的非线性性质;第二部分由一个线性动态子系统表示,用于解决整个系统存在的线性问题。上述两部分串联组合而成经典Hammerstein模型,使其成为一个可以表征耦合现象的非线性模型[10],其模型结构如图1所示。图1中,v∈R、y∈R和u∈R分别表示为系统的控制输入、测量输出、不可测量的中间变量。

图1 Hammerstein模型结构图
本文采用经典PI迟滞非线性模型作为Hammerstein模型结构的静态迟滞非线性部分,动态线性部分由经典二阶传递函数模型表示。
1.2 PI模型
PI模型是算子类唯象模型,由有限个不同权值的Play算子或者Stop算子线性叠加而成,以此描述迟滞非线性特性现象。其中Play算子的输出不仅仅取决于阈值r和权值w,而且还和历史输入极值有关。
假设Cm[0,tE]是分段单调连续函数的一个集合,其定义域为[0,tE]。当输入v(t)∈Cm[0,tE]时,对于阀值r≥0的线性Play算子Pr可定义为[11]:
Pr[v](t)=fr(v(t),Pr[v](ti))
(1)
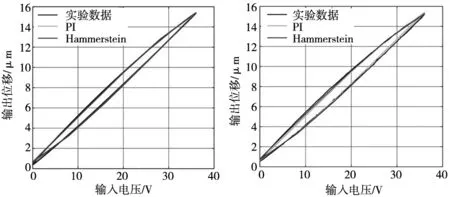
式中,ti fr(v,u)=max(v-r,min(v+r,u)) (2) 式中,u(t)是算子的输出;0=t0 u(0)=Pr[v](0)=fr(v(0),u0) (3) 且u(t)=Pr[v](t)=fr(v(t),u(ti)) (4) 式中,u0是线性Play算子的初始状态条件。图2是线性Play算子的曲线示意图,可以明显看出其呈现出对称的平行四边形结构。 图2 线性Play算子示意图 对于有限个具有不同阈值的Play算子进行线性加权叠加,可得到PI迟滞模型输出表达式为: (5) 式中,wj为Play算子的权值,且满足wj>0;m为Play算子的数目;rj为Play算子的阈值。 一般情况下,阈值rj的选取原则是等间隔选取,定义为: (6) 此外PI模型的精度与算子的数量有极大的关系,当算子数量有所增加时,其模型精度也会随之有所提升,但与此同时算子数量的增加同样会降低模型的运算速度。因此为了平衡PI模型的精度和运算速度之间的关系,选取合适的算子数量就显得十分重要。经过多次试验,本文选取的算子数目为9个。 压电定位平台系统的主要结构为压电驱动器、柔性铰链和基座等,其中压电驱动器作为主要驱动元件。在输入电压信号的作用下,通过压电驱动器驱动产生力,经由柔性铰链的联动作用进行机械运动,此时定位平台会输出较小的位移。压电定位平台系统由于其特殊的材料性质,其线性动态特性可以等效为经典质量-弹簧-阻尼系统。因此,压电定位平台系统线性动态模型可以被描述为[12]: (7) 式中,y(t)表示为压电定位平台的输出位移;F(t)表示为压电驱动器所产生的力;m是压电定位平台的等效质量;b1是压电定位平台的等效粘性摩擦系数;b2是压电定位平台的等效刚度系数。 在实际控制系统中,通常使用线性系统的离散表达形式: A(z)y(t)=B(z)u(t)+ε(t) (8) 式中,ε(t)为误差项;u(t)为Hammerstein模型中静态PI迟滞非线性模型输出,且u(t)=F(t);A(z)=1+a1z-1+a2z-2+…+anaz-na;B(z)=b1+b2z-1+b3z-2+…+bnbz-nb+1;z-1是单位迟滞算子。 将离散形式模型写为传递函数形式为: (9) 以v(k)作为整个平台系统的输入电压,则压电驱动器产生输出力F(k),也即中间变量u(k)与迟滞模型的输出之间的关系为: u(k)=P[v](k) (10) 式中,P[v]为迟滞算子。 经多次实验测定,本实验平台的动态特性符合二阶传递函数的形式,选取二阶离散传递函数能够有效表征压电定位平台系统自身特性。 由文献[7]可知,当系统的输入信号频率处于低频(频率小于或者等于10 Hz)时,此时系统趋于静态,静态特性为系统的主要特性;当系统的输入信号频率处于中高频(频率大于10 Hz)时,系统的动态特性占据为主要特性。但无法否认的是,即使是低频情况,系统之中依然存在系统的部分动态特性。经实验研究,当系统处于不同频率下,其动态迟滞非线性会有所不同,所以,本文在此研究基础上,建立了率相关二阶离散传递函数,其参数会在不同频率下进行动态自适应调整,分别在系统的低频与中高频状态下辨识出不同的传递函数的参数,使其参数能够较好的适应频率变化,可以更好地拟合系统本身的迟滞特性。 本文中的Hammersein模型的参数辨识步骤分两步进行,其中分别是静态非线性PI模型的权值参数辨识和动态线性经典二阶传递函数的辨识。通过构造输入信号v(t)和采集实验测量输出数据y(t)构成辨识所需的实验数据,从而进行上述模型的参数辨识。 当输入电压频率较低时(一般为小于或者等于10 Hz),压电定位平台系统的迟滞现象没有发生大的变化,此时可以近似认为整个系统的迟滞环没有变化,此系统具有准静态特性。给定压电定位平台系统正弦输入信号v(t)=10sin(2πft)+10,其中频率f为1 Hz,测得压电定位平台系统的输出位移y(t),构成辨识PI静态非线性迟滞模型的实验数据,进行辨识。 PI静态非线性迟滞模型主要辨识参数为其各个算子的权值wj,j=1,2,3,…。针对上述模型,利用其离散形式: (11) 式中,Prj[v](k)为PI模型的Play算子输出;wj为Play算子对应的权值,亦为待辨识参数。 定义y(k)为实验平台实际测量所得的位移输出,则所建立模型与实际平台所测量的误差值为: e(k)=y(k)-P(k) (12) 式中,e(k)为实际位移输出与PI模型输出的误差项;P(k)为PI模型输出。 以误差项的平方和作为辨识所需的准则函数,则定义最小误差准则函数: Jmin=eTe (13) 本辨识方法采用非线性最小二乘法,选取Play算子个数为9,对上述模型进行辨识,辨识结果为w0=0.334 4,w1=0.071 4,w2=0.032 2,w3=0.007 2,其余算子权值取值较小,在此均设置为0。 (14) 系统在中高频状态下的输入-输出动态特性的传递函数的离散形式为: (15) 在本文中,基于压电驱动器的压电定位平台系统的结构如图3所示。整个实验系统主要包括以下几个部分:①实验压电位移台PS1H80-030U;②压电驱动器PH301;③信号发生器SAB101;④显示与接口面板和作为控制器的实验计算机。 图3 压电定位平台系统 其中,实验压电位移台包括移动平台、压电驱动器和位移传感器,位移传感器的分辨率2 nm,移动平台的最大位移距离是30 μm。整个实验系统的工作过程为:信号发生器输入0~10 V的电压信号,由功率放大器放大后输入电压范围变为0~150 V、频宽6 kHz的电压信号,经显示与接口面板输入到压电驱动器作为压电定位平台的驱动电压,通过位移传感器测得位移平台的输出位移,经柔性铰链放大后其输出位移距离范围为0~100 μm,全过程由作为控制器的实验计算机采集信号并进行保存。在本文中,控制器的采样时间是0.5 ms。 为了检验所提出的Hammerstein模型的精确度,本文采用均方根误差ERMSE和相对误差ERE作为验证模型精确度的指标,其中,均方根误差ERMSE和相对误差ERE定义为: (16) (17) 式中,L为采集数据个数;y(k)为实际采集得到的压电定位平台系统的位移输出;ym(k)为Hammerstein模型的预测输出。 压电定位平台系统的实验输入输出迟滞关系,与PI模型输入输出迟滞关系、Hammerstein模型输入-输出迟滞关系如图4~图6所示。 (a) 1 Hz (b) 10 Hz (a) 1 Hz (b) 10 Hz (a) PI模型 (b) Hammerstein模型 根据实验测试结果,由图4显示可知,随着输入电压信号频率的增大,迟滞非线性特性也逐渐变得严重,迟滞环明显变得越来越宽,显示出了强烈的率相关特性。而PI模型只能描述对称的率无关迟滞特性,随着频率的增大则无法有效地表征实验平台系统的动态率相关的输入-输出迟滞特性。相比较而言,本文所提出的Hammerstein模型包含有一个动态线性子系统部分,它可以描述系统的率相关动态特性。其中的动态线性子系统部分为率相关的二阶传递函数,不仅能够表征整个系统的机理动态特性,还能够有效地表征系统的迟滞率相关特性,从图4~图7和表2、表3显示结果可知,Hammerstein模型能够有效地表征实验平台系统的迟滞输入-输出特性。 图7 PI模型和Hammerstein模型在混合频率下误差曲线图(f=5/40/80) 由表1、表2的数据可以知道,Hammerstein模型相较于PI模型,其与实验平台系统实际测得输入-输出拟合更好。当输入信号频率为低频10 Hz时,PI模型和Hammerstein模型的均方根误差ERMSE分别为0.182 1 μm和0.103 6 μm,降低了43.11%,相对误差ERE由1.90%降到1.08%;当系统输入频率提高到中高频率时,传递函数的参数进行动态调整之后,尤其是在高频情况,在输入电压频率为100 Hz时,Hammerstein模型的均方根误差ERMSE为0.133 7 μm,相比于PI模型的1.063 7 μm,降低了87.43%,相对误差ERE由PI模型的11.2%降低到Hammerstein模型的1.14%;除此之外,在输入信号为混合频率情况下,PI模型和Hammerstein的均方根误差ERMSE分别为0.155 3 μm和0.113 1 μm,降低了27.17%,相对误差ERE从2.76%降低到2.01%。通过以上数据分析可知,串联了率相关动态特性传递函数的Hammerstein模型能更为有效地表征压电定位平台系统的迟滞输入-输出特性,尤其是在高频情况下,其优势更为显著。 表1 PI模型、Hammerstein模型的均方根误差ERMSE 表2 PI模型、Hammerstein模型的相对误差ERE 针对压电定位平台系统中存在复杂输入-输出动态率相关的非线性迟滞特性问题,本文提出了一种率相关动态Hammerstein模型。根据平台在不同输入信号频率下的实验性质,本文使用PI模型表征了平台的迟滞非线性特性,并提出率相关动态Hammerstein模型,可以分别在低频段和中高频段下精确描述平台的动态率相关性质。实验结果表明,对实验平台施加1~100 Hz以内的电压信号, Hammerstein模型得到的预测位移和实测位移的相对误差在1.5%以内,充分说明了所提出率相关Hammerstein模型能够更为有效地表征压电定位平台系统的复杂迟滞输入-输出特性。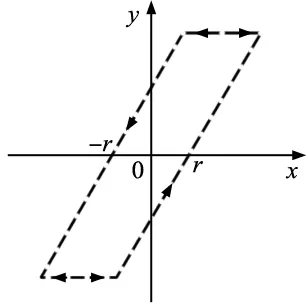
1.3 二阶传递函数模型
2 参数辨识
2.1 PI静态非线性迟滞模型参数辨识
2.2 动态线性传递函数模型参数辨识

3 实验验证
3.1 实验设备

3.2 Hammerstein模型辨识结果验证与分析






4 结论

