动态环境下基于IVS算法的多机器人路径规划*
董 海,关甜甜
(沈阳大学a.应用技术学院;b.机械工程学院,沈阳 110044)
0 引言
随着时代发展,很多领域开始应用移动机器人技术,尤其是路径规划技术。在生产领域,用于物料搬运的AGV,在快递分拣中用于无人分拣小车和派送机器人等。按照生产需求,充分利用周围环境,以感知、建模、规划、执行的标准路径规划方法执行[1-2]。按照路径规划环境是否已知,可将其分为全局路径规划和局部路径规划;根据路径规划环境中是否存在动态障碍物,可分为静态路径规划和动态路径规划[3-4]。
赵伟等[5]基于双层优化A*算法和动态窗口法,提出改进A*算法,通过一层和二层全局优化降低机器人路径的转折次数,验证了该方法适用于动态和静态环境,实现有效避障和路径规划;XIONG等[6]针对动态环境下蚁群优化路径规划中存在的收敛速度慢、全局搜索能力差和未知动态障碍物等问题,提出了一种基于时间禁忌策略的改进蚁群优化算法,改善搜索弱点,应用网格预测模型解决实时避障问题;AJEIL等[7]提出一种修正频率蝙蝠(MFB)算法,在环境中没有障碍物时生成机器人路径,当检测到障碍物时开启第二种模式进行避障,验证提出的算法可以实现规划的路径更短,且过程中无碰撞; ZHANG等[8]提出了一种动态环境下移动机器人的预测路径规划算法,在预先搜索全局近似最优路径的前提下,根据移动机器人自身和动态障碍物的速度对其进行简单的运动预测,仿真证明该算法使路径规划速度加快并降低路径代价和碰撞概率。ELMI等[9]在动态和未知环境中,提出了一种基于蚱蜢算法的新型路径规划方法,对比得到该方法在运行时间、稳定性和效率等方面具有良好的应用前景。
本文采用改进虚拟弹簧算法对机器人群的行进路线进行规划。传统虚拟弹簧算法,虽然环境适应性好,但是规划出的路线不平滑,易受环境影响,且环境越复杂路线越曲折。本文以最短路径和最短时间为目标,结合动态环境的情况,综合考虑车间可能出现障碍物的不确定情况,有效提高处理障碍物的效率,降低避障时间;同时,在MATLAB软件进行仿真,验证其有效解决局部最小值和GNRON问题的能力,及具有良好的路径规划能力和避障功能。
1 模型建立
1.1 多机器人网格的逻辑拓扑
假设每个机器人只接受相邻机器人的消息,没有任何通信延迟。其中,n个机器人都通过虚拟弹簧相互连接。图1为K=4和K=6的拓扑网络。本文以K=6的拓扑模型为例,领导者机器人为第一层,是机器人(f1~f6)的父节点,每个机器人都有自己的子节点。

(a) K=4的拓扑网格 (b) K=6的拓扑网格
假设弹簧的自然长度为l0,实际长度为lr。机器人间的弹簧控制规则如下:
①当l0≤lr时,机器人f1和f2都将受到Fp的力,且与弹簧变形方向相反;若l0>lr时,机器人f1和f2都将受到力Fs,方向与弹簧变形方向相反;②当机器人f1的节点消失时,将机器人f1和f2之间的两个弹簧视为一个被拉伸的弹簧,力的方向Fp与弹簧的变形方向相反。
1.2 多机器人的编队控制
目前,常用的编队控制[10]方法有3种:领导者-跟随者[11]、基于行为的方法[12]和虚拟结构法[13]。本文应用领导者-跟随者编队法。机器人R1是领导者机器人,可以确定每个跟随机器人Rfi(i=1,2,…,n)的运动。
空间中两个机器人fi和fj用弹簧相连,它们之间的伸缩量为d,λ为刚度系数,弹簧受力表达式为:
F=λd
(1)
式中,依据经验值将λ设置为1000。
在运动过程中,虚拟弹簧状态Tij有松弛、压缩和拉伸3种状态,表示为:
(2)
式中,lrij为机器人fi和fj之间弹簧的物理长度,根据胡克定律,机器人fi和fj之间的虚拟弹簧力表示为:
Fij=Tijk0|l0-lrij|
(3)
为避免式(3)中机器人存在碰撞的可能,定义ls为机器人的期望安全距离,则表达式为:
(4)
Fij是矢量,指向弹簧的变形方向,角βij是机器人fi和fj之间的角:
(5)
则每个机器人的控制率可以表示为:
(6)
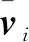
距离估计函数运用曼哈顿距离,表达式为:
D=abs(xij-xtarget)+abs(yij-ytarget)
(7)
式中,xij和yij分别表示机器人当前位置的横纵坐标;xtarget和ytarget分别表示机器人目标位置的横纵坐标。
判断依据为弹簧的弹性势能G,G越小,控制效果越好。能量函数可以表示为:
(8)
1.3 目标约束采样
本文结合目标偏执和位置约束两个方法,以提高采样的目标导向性[14]。设置目标偏执概率ppz为0.1,其次根据均匀概率随机产生一个概率值p,若该p (9) 式中,Rr为随机采样函数。 若随机生成采样点,需要约束其位置。随机生成的采样点,对比其在X或Y方向比前一个采样点更接近目标点作为依据。采样约束示意图如图2所示。 图2 采样约束示意图 融合多机器人避障规划的姿态信息和误差反馈跟踪调节方法[15],定义多机器人避障的表达式为: (10) 式中, p(k)=Rn (11) 式中,H(k)为多机器人避障中的障碍物矩阵;p(k)为多机器人群绕坐标系各轴的惯性协方差矩阵;若p(k)∈Q2(0,∞),I、J、L、O为多移动机器人质心分布矩阵参数;n为控制约束的自变量维数,为正整数;ΔI1、ΔJ1为多移动机器人避障隐态误差增益。 基于式(10),多机器人避障规划的控制器表达为: (12) 考虑动态环境下的避障功能,引入动态A*算法中的估计函数: f(x)=g(x)+h(x) (13) 式中,f(x)为节点x的估价函数;g(x)为状态空间中从初始节点到x节点的实际代价;h(x)为从x节点到目标节点最优路径的估计代价。 当多机器人距离障碍物足够近时,障碍物产生排斥力Frep,排斥力与多机器人障碍物之间的距离成反比,并指向远离障碍物的方向。Fa是Fatt和Frep的合力,机器人群将朝着合力的方向运动,直到到达目标。虚拟弹簧受力分析如图3所示。虚拟弹簧受力分析表达式如式(14)所示。 图3 作用在机器人群上的虚拟弹簧受力分析图 (14) 为了避免碰撞,当Frep (15) 式中,q0为障碍物坐标;f(q-q0)为机器人群与障碍物间的距离,迎面距离为障碍物的最大冲击距离。 虚拟弹簧中储存的弹性势能表达为: (16) 式中,Gg(q)为机器人群与目标之间虚拟弹簧的势能;G0(q)为机器人群与障碍物之间虚拟弹簧的势能。 传统虚拟弹簧算法的不足是易陷入局部最小值或者GNRON问题,如图4和图5所示。 图4 局部极小值时的路径图 图5 GNRON时的路径图 由于机器人群在转向上的时间能量耗费比直线行驶要多,所以在传统虚拟弹簧算法基础上加入转向代价,估价函数表达为: f′(x)=g(x)+h(x)+ε0 (17) 式中,ε0为转向代价,其值为: (18) 假设空间中的目标与障碍物分布图如图6所示。机器人群连接起点O和目标点A形成OA,当OA不穿过任何障碍物,机器人群路径规划图如图7所示。 图6 目标与障碍物之间分布图 图7 机器人群路径规划图 当OA穿过障碍物时,机器人群以当前位置为中心旋转,直到OA不穿过任何障碍物为止。旋转后的矢量记为OB,轴向旋转的转角为γ,搜索点为T1,该点可满足以下方程: BT1·OB=0 (19) |BT1|=d (20) (21) 根据式(19)~式(21)可得T1唯一的位置,视为虚拟目标,OT1为第一子路径,当机器人群到达T1,若T1A通过障碍物,按照得到T1的方式,可得其它虚拟目标T2,T3,…,Tn,直到TnA不跨越任何障碍物,若机器人群当前位置O与所有虚拟目标点连接,最终目标与有向线段连接,即为机器人群从局部极小点到最终目标的期望最优路径。本文基于MATLAB进行仿真,结果如图8所示。为评估算法的可靠性,计算弹性势能Eg(q)如图9所示。 图8 机器人实际移动路径图 图9 机器人间弹性势能Eg(q)图 从机器人群轨迹可看出,实际路径与图7规划的路径非常接近,成功到达目标。图9显示了机器人群到达各个虚拟目标和最终目标的弹性势能情况,该图可匹配图8中的轨迹。 在多机器人系统中,机器人群的目标还包括编队[16]。在动态环境下,机器人群实时更新附近障碍物情况以此判断哪个方向位置为最佳。采用IVS算法的多机器人动态路径规划的流程图如图10所示。 图10 多机器人动态路径规划流程图 为评估所提的策略和算法的性能,设置机器人群步长为0.06,仿真中所有参数均视为无量纲数。 机器人群之间虚拟弹簧的松弛长度l0=3,刚度因子k0=300。障碍物位置均为随机分布,障碍物的虚拟弹簧松弛长度β=1000,刚度因子kr=600,领导者机器人的目标位置坐标为(68,68),刚度因子kg=6。6个机器人穿越并避开随机障碍物的路线和弹性势能图如图11所示。 由图11a中可得,机器人群路径规划过程中没有发生任何碰撞。如图11b中的弹性势能走向可得,该图与轨迹匹配,验证底层控制效果良好。 (a) 6个机器人穿越并避开随机障碍物路线图 (b) 6个机器人之间的弹性势能图 领导者机器人和跟随者机器人穿越并避开随机障碍物的初始状态如表1所示。领导者机器人和跟随者机器人穿越并避开固定障碍物的初始状态如表2所示。 表1 领导者机器人和跟随者机器人穿越并避开随机障碍物的初始状态 表2 领导者机器人和跟随者机器人穿过并避开固定障碍物的初始状态 设置l0、k0、β=1000、kr同上。领导者机器人的目标位置坐标为(30,65),刚度因子kg=6。6个机器人穿越并避开固定障碍物的路线和弹性势能图如图12所示。 (a) 6个机器人穿越并避开固定障碍物路线图 (b) 6个机器人之间的弹性势能图 从图12a中可以明显看出,机器人群保持原有队形,成功到达目标,且无碰撞。图12b验证了多机器人在编队控制方面表现出了良好的性能。 3.2.1 路径平滑比较 程传奇、王殿君等[17-18]基于传统A*算法提出动态A*算法,适用于典型的动态路径规划。本文模拟车间的动态环境,将IVS算法与传统的虚拟弹簧算法和动态A*算法进行比较。 参数θ、§、γ的选取为平滑处理路径节点的重要环节。经过多次仿真实验的结果得出,θ=125°,§=56°,γ=2时路径平滑处理效果最好。路径平滑处理的参考标准有3种:累计转角、平均转角和路径长度。采用3种算法生成的路径图如图13所示。不同算法路径平滑处理对比表如表3所示。 图13 3种算法生成的路径对比图 表3 不同算法路径平滑处理对比表 由表3可得,IVS算法相比于传统VS算法和动态A*算法,累计转角分别降低了79.07%和25.63%,平均转角分别降低了41.83%和29.14%,路径长度分别降低了61.76%和18.69%,采用IVS 算法规划处的路径更加平滑。 3.2.2 最短时间和最短路径比较 为适应更多障碍物环境,本文覆盖率分别在8.6%、17.2%和28.4%的环境下仿真比较,如表4所示。 表4 不同算法下机器人路径规划的路径长度与时间对比表 由表4可得,IVS算法相比于传统VS算法和动态A*算法,在障碍物覆盖率为8.6%时,路径规划的时间和路径长度分别减少了38.1%和18.75%;在障碍物覆盖率为17.2%时,路径规划的时间和路径长度分别减少了33.33%和18.18%;在障碍物覆盖率为28.4%时,路径规划的时间和路径长度分别减少了23.43%和10.91%。 3种算法的路径规划时间和路径长度对比图如图14和图15所示。 图14 3种算法的路径规划时间随环境变化折线图 图15 3种算法的路径规划长度随环境变化折线图 由图14得出,随着环境大小的增大,应用本文算法使得时间增长的幅度明显低于其他两种算法。可证,本文提出的算法更优。 图15可得,随着环境大小的增加,应用本文算法使得路径长度增长的幅度更小,可证,IVS算法在机器人行走路程上短于采用其他两种算法的多机器人行走路程,验证本文算法在路径规划上的搜索效率高和收敛速度快的特点。 在仿真环境下,以(4,0)为起点,(35,45)为目标点进行动态环境下得路径规划能力验证,在路径中选取两个局部子目标点,设置为P1,P2,如图16所示。本文设定障碍物的行驶速度小于机器人群的行驶速度。 图16 局部子目标点位置图 图16中,路径被分为目标点-P1;P1-P2和P2-目标点。机器人群在P1-P2路径内,检测到前方有障碍物出现(黑色方块),若按原路线行驶,将会在灰色方块位置发生碰撞,如图17所示。由于障碍物和机器人群的行动轨迹交于一点,需要对P1-P2段路径进行局部规划,如图18所示。 图17 机器人位于P1点 图18 机器人位于P2点 P1-P2段原路径用虚线表示,其他两段路径用实线表示。由图17和图18可证,应用IVS算法可实现动态环境下的避障,且避障能力充足。 (1)提出IVS算法,可规划出最优路径,且具有搜索效率高、避障能力强的特点。 (2)采用IVS算法可以有效解决局部最小值和GNRON问题,且实现实时避障。 (3)将IVS算法、传统VS算法与动态 A*算法对比,验证应用IVS算法得到的路径更加平滑,能够适应不同障碍物密度环境,且有效避开动态障碍物。
1.4 避障控制策略
2 改进虚拟弹簧算法(IVS算法)



2.1 基于IVS算法的多机器人路径规划
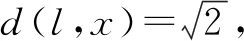


2.2 多机器人编队路径规划

3 仿真分析
3.1 多机器人编队路径规划




3.2 算法比较




3.3 动态环境仿真


4 结束语

