类比法在RLC串联电路分析中的应用
张宏根
(浙江省杭州学军中学,浙江杭州 310000)
物理学中不少不同部分的知识点之间有着紧密的联系,挖掘它们之间的关系,有助于理清物理学的知识脉络,并能够使所学的知识融会贯通.物理学习的研究方法很多,其中类比法是较为常见的一种研究方法.类比法指的是由一类事物所具有的属性,推测出其它类似事物也具有这种属性的一种推理方法.[1]这种方法能把具有相似之处的物理知识点放在一起进行对比,从而起到帮助记忆、加深理解,提高分析问题和解决问题的能力.[2]通过近年来的中学物理教学工作,笔者深刻认识到在教学中传授知识固然重要,但掌握好的学习和研究方法则可以让我们的学生终生受益.因此,在物理教学中教师应该注重传授物理学的研究方法,使学生学会运用这些方法解决问题,尤其是针对学习物理竞赛的学生,显得尤为重要.以下笔者就以RLC电路为例,探索类比法在物理学习和解题中的应用.
1 RLC串联电路的类比研究
物理中的不同知识点之间可能存在关联性和相似点,比如RC电路与RL电路,RLC 串联电路和LC电路分别与阻尼振动和简谐运动之间都具有很大的相似性,因此可以通过类比,将一种研究方法应用到另一种上,从而快速得出结论.以下就举例作简单的说明.
1.1 RC和RL串联暂态电路的类比
图1 显示的是RC 串联电路,其中电源电动势为E,电容为C,电阻为R.电容器充电后将电键开关接到2 的位置,电容器C通过电阻R放电,在放电的暂态过程中,电流i随时间t的变化关系可以通过基尔霍夫第二定律得到,具体如下.[3]
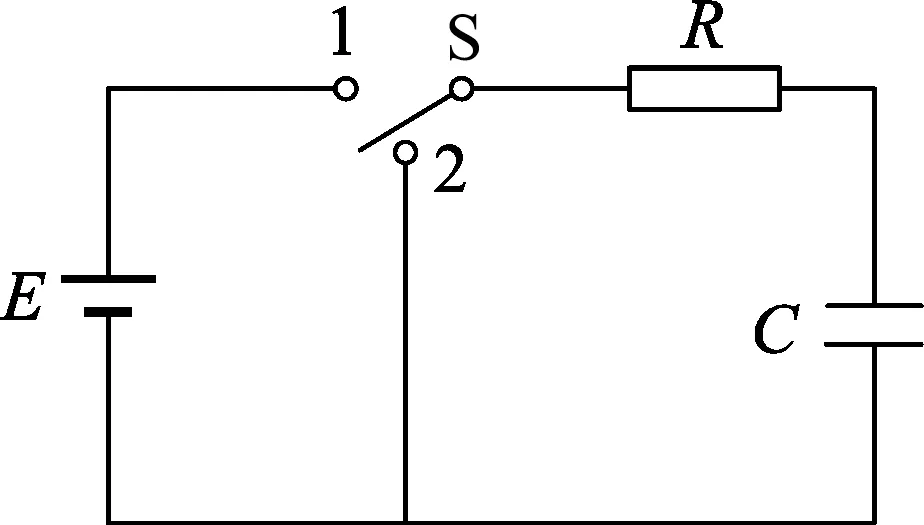
图1 RC串联电路示意图

通过对(1)式求导,并结合(2)式,得到RC 电路在放电暂态过程中的电流,即
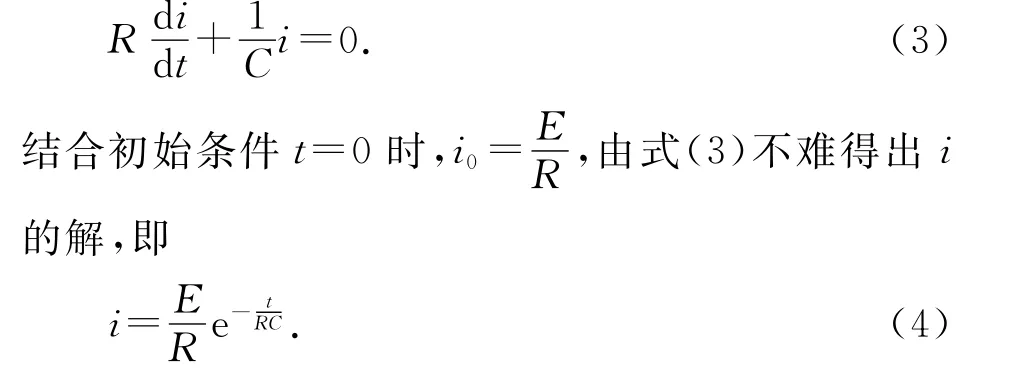
可见,电路中的电流以指数形式变化,定义RC 串联电路的时间常数τ=RC.
图2显示的是RL串联电路,其中电源电动势为E,电感为L,电阻为R.对比图1和图2,不难发现二者有很大的相似性,因此,可以类比RC 电路来分析RL 电路.当电键开关从1快速拨向2时,设初始条件t=0时,i0=.可以通过基尔霍夫第二定律,类比RC串联电路的(1)式,可以得到[3]
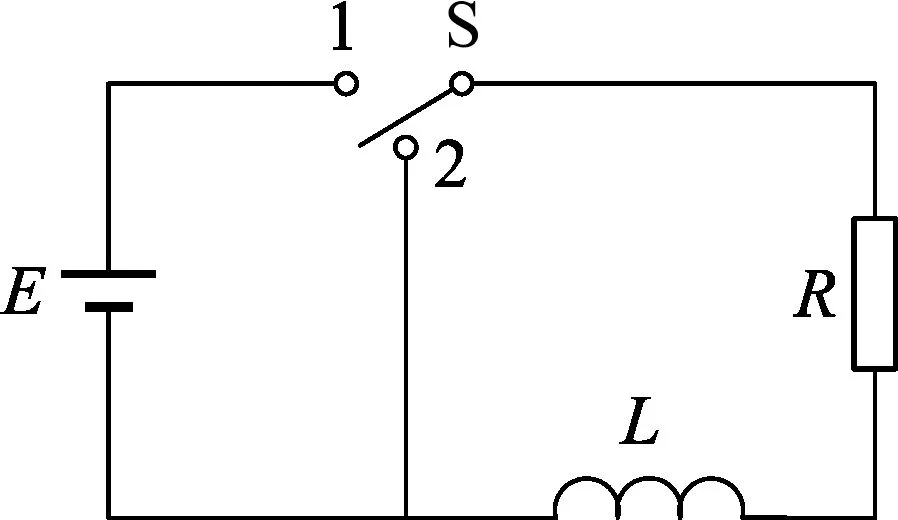
图2 RL 串联电路示意图

将(5)式和(3)式对比,不难发现二者高度相似,所以可以类比得出(5)式的解

通过以上对比分析不难得出短接的RC和RL电路暂态放电过程具有很大的相似性,表1 是二者的对照关系.
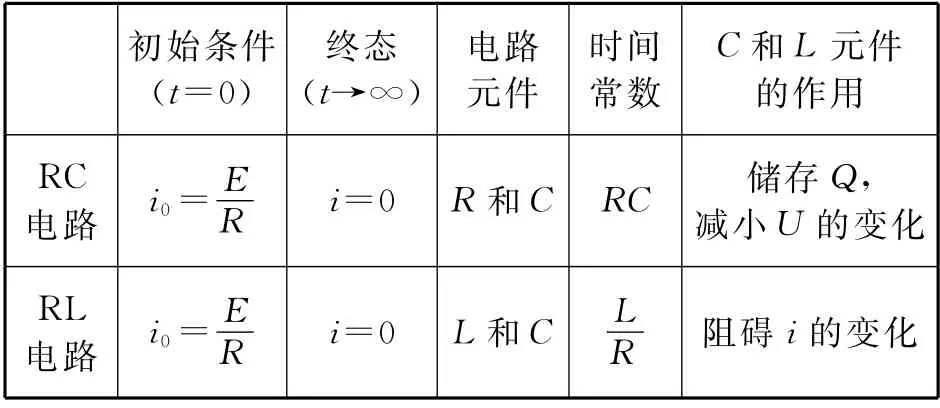
表1 短接的RC和RL电路暂态过程对比
1.2 RLC串联电路和阻尼振动的类比
图3 显示的是RLC 串联电路,其中电源电动势为E,电容为C,电阻为R,电感为L.假设电键开关从1快速导通到2,则在放电的暂态过程中,电流i随时间t的变化关系可以通过类比上述RC和LC 电路方法,由基尔霍夫方程得到,具体如下.[3]

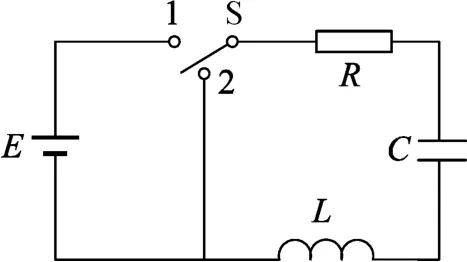
图3 RLC串联电路示意图
将(2)式代入可得
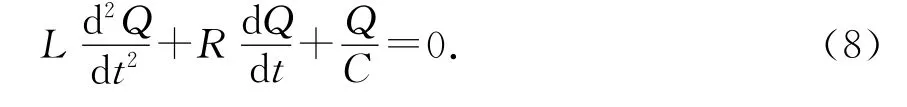
此式与阻尼振动,即物体以不太大的速率在黏性介质中运动时,其阻力与运动的速率成正比(f=-γv)情况下的微分方程类似,可以对两者进行类比.其中阻尼振动方程如下.[4]


综上所述,RLC、LC 串联电路分别与阻尼振动、简谐运动类似,其对应的电路物理量和振动的动力学物理量之间的对应关系如表2所示.
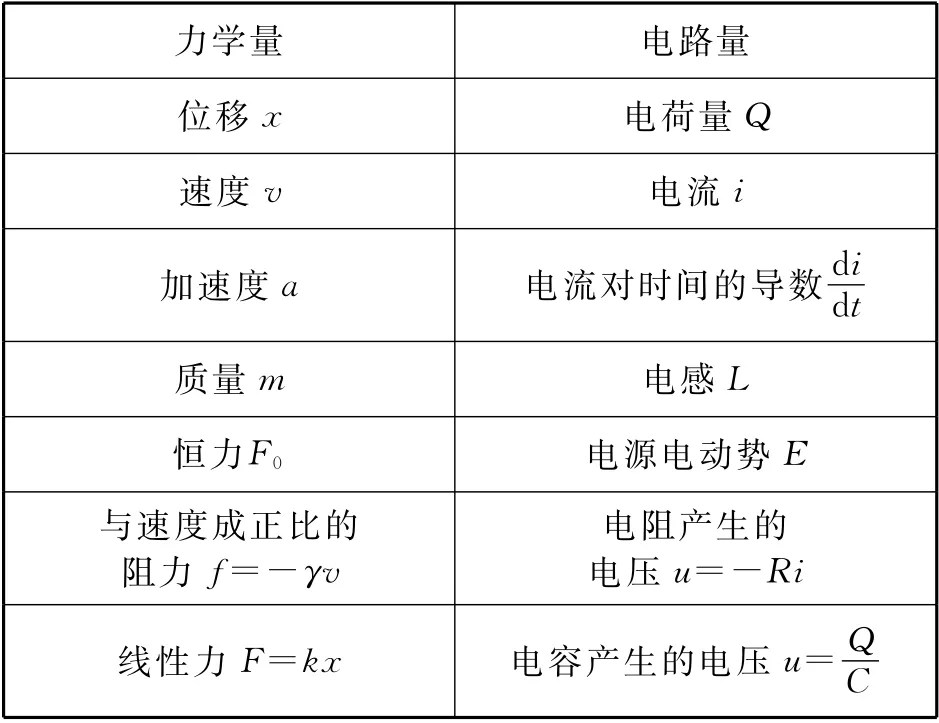
表2 RLC电路和振动的动力学各物理量的对应关系
2 类比法的应用举例
通过前述的类比我们发现:RLC 电路和动力学振动之间有极大的相似性,这种相似性表现在其方程的同构上.所以很有必要探索利用RLC 电路的相关知识来求解与之相似的动力学振动问题,或者利用动力学振动知识来求解RLC 电路问题,以期获得更为简洁的求解方法.以下就以两个相关的高中物理题举例说明.
例1.如图4,竖直匀强磁场B中放有两条平行无限长导轨,间距为l,导轨光滑无摩擦且为理想导体.在导轨上平行放着两根完全相同的质量为m的导体棒,每根棒上串联有电阻R,电容C,导体棒与导轨接触良好.初始时,棒1具有指向棒2 方向的速度v0,电容上无电荷,两棒间距足够大不会相撞.
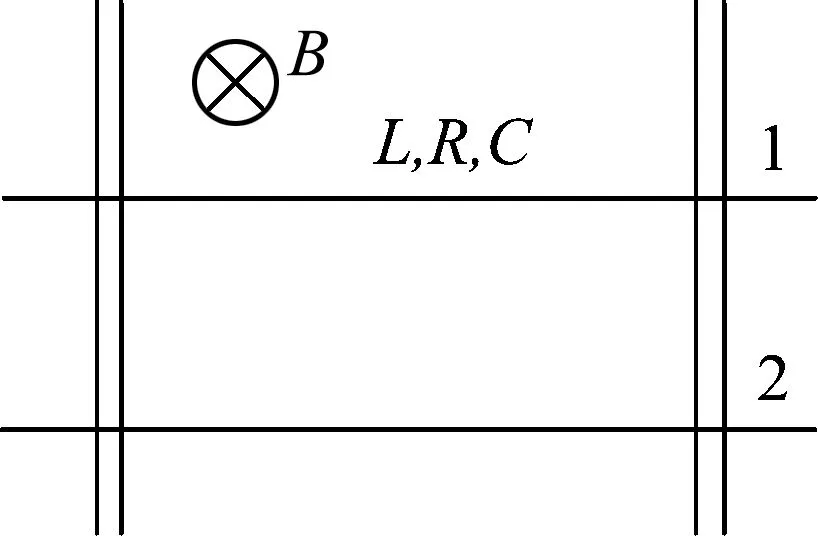
图4
(1)求出电流随时间变化关系.
(2)将题中的电阻改成L的电感,其余不变,求电流随时间变化关系.
解析:此题的导体棒以一个初速度运动,可以类比为已经充电的电容器,其电压可以用导线切割磁感线产生的电动势Blv0来表示.在随后的运动过程,可以类比为RC的放电暂态过程和LC 电路的自由振荡过程.具体求解方法如下.
(1)如图5,假设两导体棒的运动速度分别为v1和v2,电流流向如图5 所示.由牛顿第二定律可得

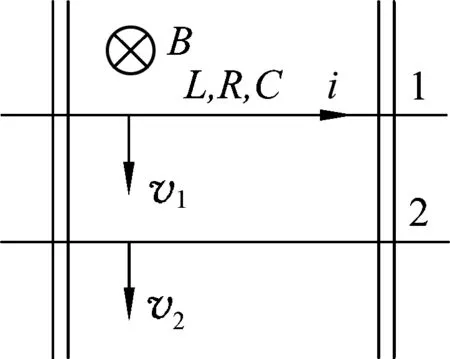
图5
根据基尔霍夫第二定律,可得
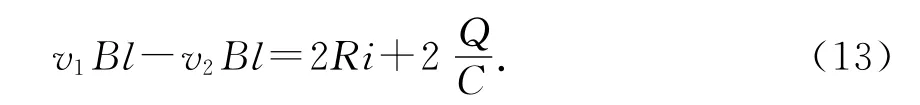
两边求导,并结合(11)、(12)和(2)式,可得
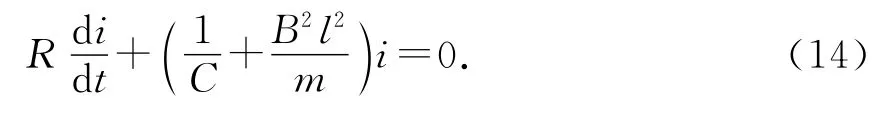
令

则总电容就为C′,(14)式可以写成

(2)当电阻改为电感L时,根据基尔霍夫第二定律,并类比(13)式可得
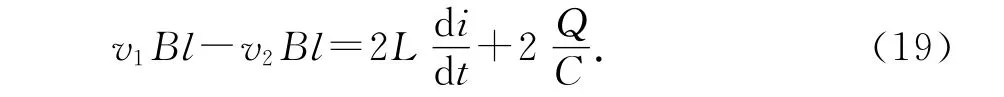
两边求导,并结合(11)、(12)和(2)式,可得
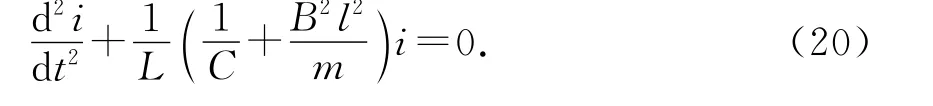
将(15)式代入可得

将(21)式和简化的(8)式相比较,可以看出:两式具有完全一致的形式,所以串联电感的导体棒的运动过程可以类比为LC振荡电路.对照(10)式的解的形式,将串联电感电路中的C′、E0(=Blv0)分别和LC 振荡电路中的C、E作类比,不难得出(21)式的解

例2.如图6所示,一个磁感应强度为B的均匀磁场,垂直于一轨距为l的导轨平面,轨道平面与水平面有α的倾角.一根无摩擦的导体棒,质量为m,横跨在两根金属导轨上.若开关依次接通1、2,使电容为C或电感为L的元件与棒构成电路,当从静止放开导体棒后,求棒的稳定运动状态.
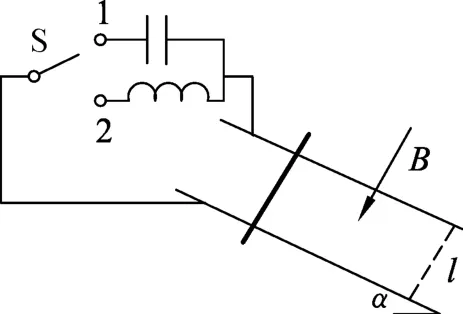
图6
解析:此题是将电容或电感与导体棒切割磁感线运动组合的一类问题.当开关接1,导体棒与电容器构成回路,导体棒开始以加速度a运动,并产生动生电动势而对电容器充电,同时电路中产生电流,此时棒会受到一个反向的安培力作用.当开关接通2,导体棒与电感线圈构成回路,棒开始运动后,随着速度增大,产生的动生电动势增大;电动势直接加在线圈两端,因此通过线圈的电流增大;而导体棒受到安培力的作用,越过平衡位置后减速,直至速度为0.电路电流开始时逐渐增大,在导体棒达到最低点时电路中电流最大.随后导体棒因安培力作用往回加速,动生电动势使电流减小,直至导体棒回到初始位置,电流减小为0.再重复上述过程,形成简谐运动.求解这类问题的常规方法是将导体棒和电容、电感分开分析,对导体棒应用动力学知识列方程;对电容、电感利用电学知识列方程.求解过程较为繁杂.我们可以根据例1的结论来进行求解,可以极大的简化求解过程,具体如下.

此时,就不需要考虑电学方面的问题,直接根据动力学知识,即牛顿第二定律就可以列出方程

此时的串联电路可以等效为LC振荡电路,得到其电流方程
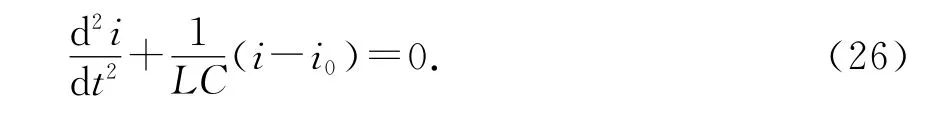
从题中不难看出导体棒也将在平衡位置附近作简谐运动,此题通过类比法,将简谐运动化为LC 自由振荡电路求解,将极大简化计算过程.
不难得出当电流最大时,为导体棒的平衡位置,此时导体棒受力平衡,即重力沿着轨道的分力mgsinα和安培力ilB是一对平衡力,即平衡位置处的电流i0为

由题意知,初始时刻t=0时的初始电流i=0,可以类比LC振荡电路的解,并结合(27)式,得出(26)的解

在导体棒与电感线圈构成回路中,电压与电流的关系为

对(29)式两边积分,由初始条件,x=0时i=0,可得

将(28)式代入(30)式中,可得
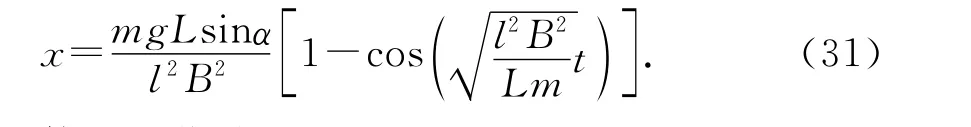
即导体棒在作简谐运动.
3 结论
通过对RC和RL 电路类比,得出二者物理量之间的相似点;通过对比RLC 电路和阻尼振动,以及LC振荡电路和简谐运动,得出电学量与力学量之间的对应关系.这种类比法不仅便于学生快速掌握相关知识点,也有利于在解题和学习中开拓思维,触类旁通.为此,通过举例,利用导体棒做切割磁感线运动时的可以等效为电容C,进而可以通过RC 和LC 电路知识来求解这类电路串联电容和电感的相关问题;或者利用B2l2C将电容等效为质量m*,利用力学方法来求解电学问题.通过例题展示不难可以发现,使用这些方法可以得到更为简洁的求解过程.

