如此拔河谁能赢？

王 强 颜文萱 周晨依 王子衿

（扬州大学物理科学与技术学院，江苏扬州 225009）

1 问题的提出

互联网上有关于“4人拔河比赛”的一段视频，其截图见图1.这个体育益智游戏很适合于学生课间活动，其中蕴含着深刻的物理内容.如图2 所示，画出其力学模型图，F1是左边大男孩的施力，F2、F3分别是右边两个男孩的施力，F4是左边小女孩的施力.请大家思考：在不考虑绳子与圆柱棒界面摩擦的情况下，哪一方胜出的几率更大？在考虑界面摩擦力的情况下，谁又将胜出？

图1 4人拔河比赛（网络视频截图）

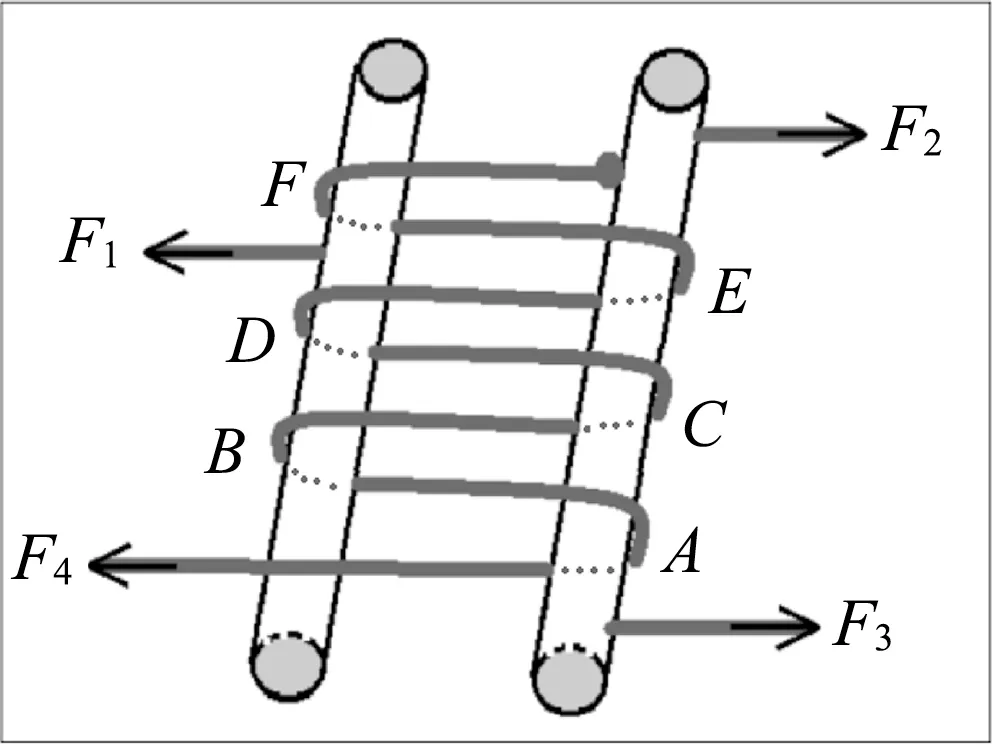
图2 4人拔河比赛施力示意图

2 问题分析

在不考虑棒与轻绳接触面摩擦的情况下，绳中各处张力相等，均为F4，因此F1＝6F4；再对杆与绳组成的整体受力分析，考虑到体系受力平衡，从而得到关系F2＋F3＝F1＋F4，从而得到F2＋F3＝7F4.若左边的女学生施加100 N 的力，则左边的男学生需要施加600 N 的力才能维持平衡.显而易见，女学生获胜的可能性更大.

那么在考虑棒与轻绳界面摩擦的情况下，左边的女学生是否还可以轻松获胜呢？我们仍然先对整体受力分析，棒与轻绳界面的摩擦力属于内力，不影响整体平衡，因此F2＋F3＝F1＋F4仍然成立.但由于受到摩擦力的影响，各股绳中的张力不再相等，4 个力之间的数量关系也因此发生改变.下面笔者应用数理结合的方法，进一步探究其中的力学规律.

假设左边的女学生施加的拉力大小为F，再设绳子与圆柱间的静摩擦因数为μ，且在图2 中A、B、C、D、E、F6处均存在摩擦.女生施加拉力欲使绳子向自己方向运动，那么每一处摩擦力和绳子拉力的大小又有着怎样的数量关系呢？采用下面的分析过程.

图3 圆柱体与绳子接触处受力示意图

我们分别在x、y方向上建立受力平衡方程，得出拉力、正压力和摩擦力的角密度随角度θ变化的表达式.

x轴受力平衡：

表1 在A、B、C、D、E、F 6个接触处各股绳上下两侧的拉力

如果左边高个子男生意欲胜出，需要把绳子拉向自己一侧时，A处摩擦力方向改变，将变得与小姑娘的拉力同向.此时左边男生所施加的拉力将变为

笔者选用了大号弹簧测力计和普通弹簧测力计进行实验验证，如图4 所示.实验结果表明：（1）当左边男生维持施力F1＝10 N 时，女生需要施加32 N 的力才能向自己一方拉动绳子；（2）当女生维持施力F＝1 N 时，左边男生施加400 N 的力都难以拉动绳子.根据实验（1）的结果，由式（7）可以推得，实际情况下木棒与棉麻绳之间的静摩擦因数μ≈0.38；进而由式（8）推知，在实验（2）中男生需要施加1842 N 的力才能拉动绳子.需要指出的是，实验过程中女生的施力不能太小，否则绳子松弛难以完成实验.

图4

综合以上分析可得出结论：在考虑摩擦的情况下，左边的女生要想把绳子拉向自己一边，几乎是不可能的；而左边男生想把绳子拉向自己一边，更是难以完成的任务.

3 结语

从生活中发现、分析并解决物理问题，是培养学生物理兴趣的重要途径.本文展示了数理结合在解决“四人拔河比赛”实际问题中的应用，有利于提升中学生的思维品质，从而提升物理学科核心素养.［1］