对双缝干涉实验亮条纹位置的几点思考
谢礼平
(南京市东山高级中学,江苏南京 211103)
高中物理新教材选择性必修第1册第4章第4节,[1]课题为“实验:用双缝干涉测量光的波长”.在该节对实验原理的阐述中,推导了亮条纹所在位置的表达式.如图1所示,与双缝中心间距d相比,每个狭缝都很窄,宽度可以忽略不计,双缝中心S1、S2的连线的中垂线与屏的交点为P0,缝到屏之间的距离OP0=L.下面针对教材在推导亮条纹位置x与光波长λ之间关系式(1)的过程提出几个问题,随后提出作者对此的思考.
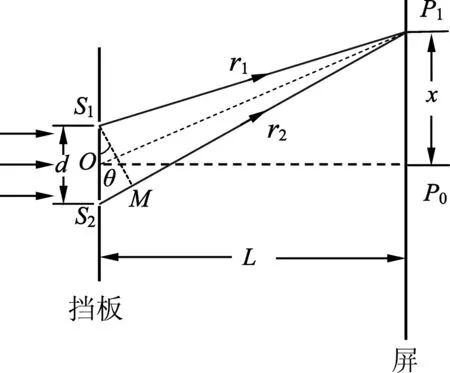
图1
1 问题1及其讨论
由教材表述的推导,会得到

教材在推导过程中有两个地方使用了近似相等.
近似1:在r1=MP1的条件下,将三角形S1S2M近似认为是直角三角形,即∠S1MS2≈90°.
近似2:sin∠P1OP0≈tan∠P1OP0,教材表述为sinθ≈tanθ.
还有一个近似相等教材没有提,而是直接表述为相等,即近似3:∠P1OP0≈θ,这个近似伴随着∠S1MS2≈90°的近似而产生.
那么,为什么要用这3个近似?这3 个近似相等有根据吗?在这里多数教师都感觉讲授起来非常棘手:完全按照教材方式去讲解,依靠学生的现有的数学基础,他们会产生各种各样的疑问:为什么要这样近似?我用另外的近似方法可以不可以?如果可以的话,会推导出与教材结论完全不相同的结论.要知道,这些近似相等要面对的是可见光波长的数量级,即10-7m,它们真的可靠吗?作者的印象是,在实际教学中,对这些问题的对待方式,要么是回避;要么是只强调教材提出的近似的权威性;只要求学生记住最后导出的关系式,推导过程略过不提.对此的疑问大都不了了之.
为确认这些近似的可靠性,作者首先考虑的是根据实验室现有实验装置提供的数据做计算,具体是以本节教材内容后第97页提供的“练习与应用3”为例,实验最可能的涉及的数据如下:单色光波长λ=6.33×10-7m,双缝间的距离d=0.3 mm,屏距离双缝(或挡板)L=1.2 m.
(1)首先研究近似1 的可靠性,即△S1S2M近似认为是直角三角形.
先计算(r2-r1),再比较它与直角三角形S1S2M的边长S2M的差距,为了获得可以与可见光波长数量级相比较的数据,计算的精度至少要到10-10m.
如图2所示,由几何关系可知
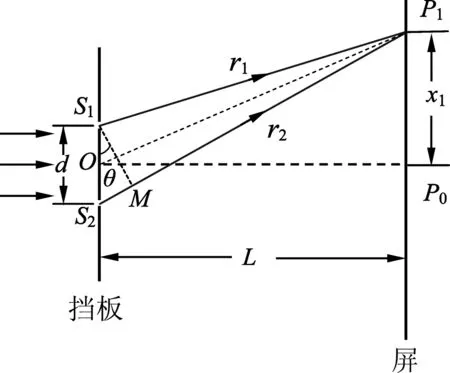
图2
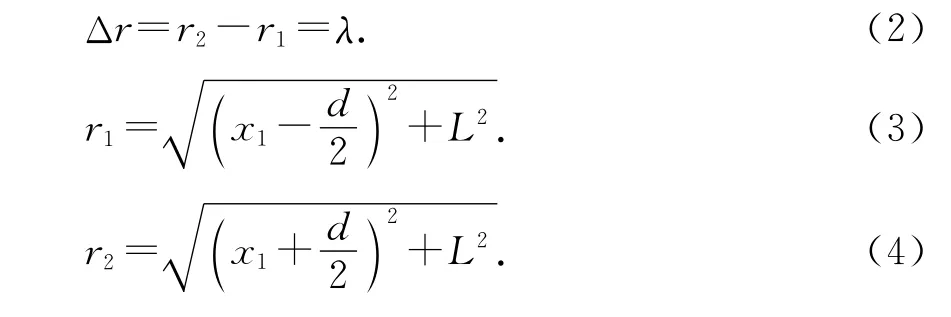
以上3式联立可得

代入数据计算,上式的每步计算均保留到11位有效数字,可得
x1≈2.5320056534×10-3m.
由此就可以计算∠P1OP0的正弦值

设S1M⊥S2P1,那么
sin∠P1OP0=sinθ.
S2M=dsin∠P1OP2.
S2M=6.3300000423 m.
由此可以看出S2M的相对误差为
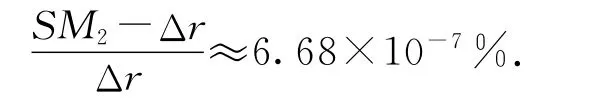
这几乎没有误差,在S1M⊥S2P1的情况下,完全可以认为Δr=S2M.
(2)从另一个视角来证明关系式(1).
由(2)-(4)式联立可以得(5)式,考察(5)式.
从刚才的计算过程知道:项“4λ2L2”的数量级为10-6m;项“λ4”的数量级为10-18m,所以分子中的项“λ4”忽略不计;而项“4d2”的数量级为10-7m;项“4λ2”的数量级为10-12m,故而分母中的项“4λ2”也可以忽略不计,
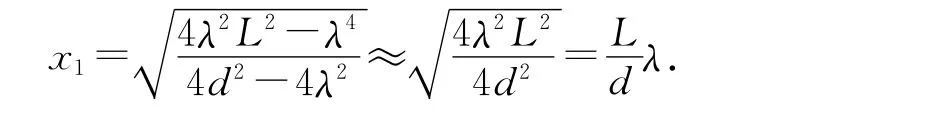
上式结合式(2)就可以得到关系式(1).这也许是高中学生较为容易接受的推导.
还可以观察一下P1P0和OP0之间的空间比例关系:

这大约相当于在12 m 远处观察一枚一元的硬币,图2的空间比例关系与实际情况不符,但图2 方便了表述和分析.
综上所述:在教材第97页“练习与应用3”提供的实验条件下,关系式(1)非常可靠.
由于采用可靠的近似,抓住主要矛盾,忽略次要矛盾,得出的这个关系式直观而简洁.
2 问题2及其讨论
双缝干涉实验中观察到的亮条纹只是有限的几条,不是满足亮条纹关系式的所有地方都有的,亮条纹的亮度也不尽相同,这是为什么呢?
这个问题的解答取决于对衍射现象的认识程度.如图3 所示,双缝干涉现象,是在两个狭缝分别产生的衍射在重叠区域叠加而形成的,具体说就是狭缝S1因衍射现象而产生的中央亮条纹宽度(主极大)S11S10,狭缝S2对应的是S21S20,两条衍射现象的中央亮条纹在它们重叠的区域S10S20产生了明暗相间的条纹,是为干涉现象.

图3
(1)可以计算重叠的区域的宽度.
设狭缝的宽度为a,中央亮条纹的宽度为S11S10=S21S20=l,光的波长为λ,挡板与屏的距离为L,则有

设重叠的区域S10S20的宽度为l′,由图3的几何关系可得l′=l-d.
由于每相邻两个亮条纹的间距几乎是相等的,可用上文所说的x1表示,所以能看到的亮条纹的数量n最多为
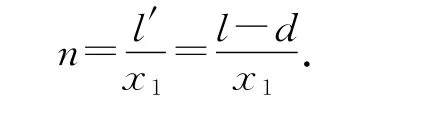
(2)继续使用波长λ=6.33×10-7m 的单色光进行实验.
由资料所提供的数据,[2]实验单缝的宽度为a=0.1 mm,再由教材第97页“练习与应用3”提供的实验参数进行计算.
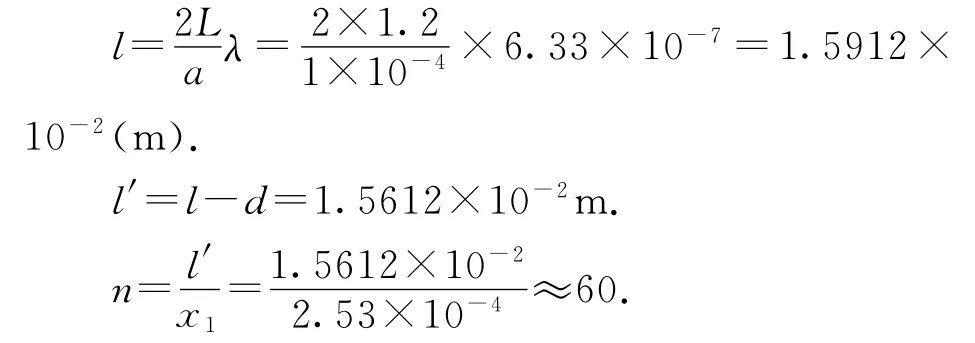
约60条是基于以上实验参数,依据理论知识计算的亮条纹的数目.实际上这些亮条纹的亮度有比较大的差异,有的甚至肉眼不见,中央部分一些亮条纹最为明亮,实验时以它们为对象进行测量.
衍射现象的次级亮条纹之间也会产生干涉现象,由于亮度的原因,它们不是实验的测量对象,此处不再赘述
3 问题3及其讨论
亮条纹之间的距离是等间距的吗?
用眼睛观察实验发现亮条纹间距是相等的,但亮条纹位置的关系式是采取近似后推导所得,因此,严格的说,间距并不相等.课本中说的等间距,也是以可靠的近似为根据的.
实验中,有时以5-9条亮条纹为对象进行测量.本文对第4 级亮条纹的位置分两种方式进行计算:一是实际计算,二是根据亮条纹的关系是进行计算,然后进行比较.
(1)实际计算.
如图4所示,对第4节亮条纹的位置P4,有

图4

以上3式联立得到
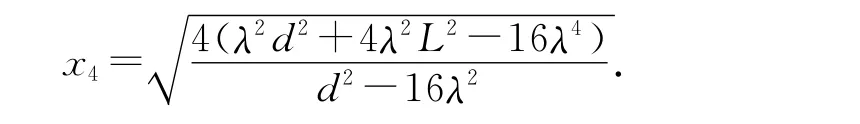
代入问题1 讨论所给数据计算,在计算时均保留到11位有效数字,会得到
x4=1.0128360667×10-2m.
(2)用关系式计算.
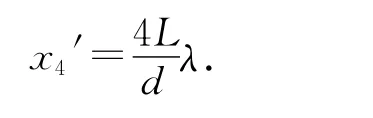
代入数据计算,得到

其误差为

它们几乎没有差别,可以认为:用关系式(1)计算第4级亮条纹位置依然十分精确,亮条纹间距可认为是均匀的,眼睛无法看出它们的差别.

