弯曲载荷下特殊螺纹接头性能有限元分析*

闫 龙，陈玉鹏，周晓锋，2

（1. 天津钢管制造有限公司，天津 300301；2. 天津大学材料科学与工程学院，天津 300350）

特殊螺纹接头广泛应用于高温高压、稠油热采以及页岩气等非常规油气资源的开发。在稠油热采及页岩气开发过程中，普遍应用水平井技术，对特殊螺纹接头的性能提出了更高的要求。在水平井中，设计井眼曲率通常为6°/30 m~12°/30 m，局部曲率可达16°/30 m。一方面，需要评估特殊螺纹接头在弯曲载荷下的结构稳定性、密封性能，防止接头失效；另一方面，在套管下井及水泥固井作业中可能需要旋转套管，以使套管顺利下入并提高固井质量。套管旋转会使接头在弯曲段承受循环弯曲载荷，由此带来的接头疲劳破坏也不应被忽略［1］。

有限元分析被广泛应用于特殊螺纹接头的设计开发，已成为特殊螺纹接头开发、适用性评价、产品线认证等方面强有力的辅助工具［2-4］。本文利用ABAQUS 有限元分析软件，对Φ139.70 mm×12.7 mm P110 TP-G2 HC 特殊螺纹接头进行了有限元分析，研究了弯曲载荷下，特殊螺纹接头的结构、密封及抗疲劳性能，为非常规油气资源开发中特殊螺纹接头的选用提供必要的参考，同时可作为理论支撑，应用于新型特殊螺纹接头的开发中。

1 有限元模型

特殊螺纹接头有限元分析通常采用二维轴对称模型，忽略螺旋升角的影响，与三维模型相比计算精度及计算效率更高，可以满足结构设计的需要。与传统二维模型有限元分析不同，由于弯曲是一种非对称载荷，不能直接施加于轴对称模型上。ABAQUS 软件中提供了解决此类问题的相关功能，但由于部分功能不能在ABAQUS CAE 中直接实现，而只能通过编辑INP 文件的方法，增加了该问题的求解难度，涉及到的难点包括：非对称轴对称单元（如CAXA4N），Slide Line（滑移线）接触算法，非均匀载荷的施加（DLOAD 子程序）。

建立了二维有限元模型，如图1 所示。在（R，θ，Z）组成的坐标系统内，轴对称模型建立在对称轴的右侧。本文选择CAXA41 作为单元类型，其中4 代表傅里叶模式，1 说明需要定义0°平面及180°平面上的特性。虽然模型只在0°平面上存在，但在180°平面上有与之对应的节点信息。详细内容可参阅相关文献［5-6］。

图1 有限元模型示意

与传统特殊螺纹接头求解过盈配合的算法不同，由于CAXA 单元的使用，面对面的接触算法不再适用，而需要引入Slide Line（滑移线）接触算法。具体来讲，将特殊螺纹接头内螺纹的接触面，包含螺纹、密封面、扭矩台肩部位，定义为滑移线，外螺纹相应位置的接触面定义为接触单元，两者间建立接触关系。

弯矩的施加通过在套管管端施加非均匀面载荷的方式实现，需要借助ABAQUS 用户DLOAD 子程序加载，弯曲应力值σz满足以下公式：

式中 M —— 弯矩，N·mm；

I —— 惯性矩，mm4；

R —— 半径，mm；

θ —— 角度，（°）。

特殊螺纹接头有限元分析通常采用弹塑性材料模型。图2 所示为Φ139.7 mm×12.7 mm P110 套管实测工程应力-应变曲线，其中弹性模量E 为206 GPa，泊松比为0.3，屈服强度Rp0.2为850 MPa，抗拉强度Rm为940 MPa，将实测的应力、应变数据转化为相应的真应力及塑性应变，输入到ABAQUS 中进行计算。

图2 工程应力-应变曲线

模型的有限元网格如图3 所示，其中全局网格大小1 mm，密封面网格尺寸0.1 mm，由于涉及到疲劳性能的计算，螺纹部分的网格需更加细化，为0.04 mm。在接箍中面施加对称边界条件，只限制轴向位移。分析过程为：上扣-施加内压-施加弯曲载荷。

图3 模型的有限元网格

首先模拟接头的上扣过程，然后按照此规格套管名义内屈服压力施加内压载荷120.7 MPa，随后在套管管端施加弯矩，对应弯曲度分别为10°/30 m~60°/30 m，逐渐增加。分析结束后，对接头的结构、密封及抗疲劳性能进行分析。

2 特殊螺纹接头密封能力评价准则

特殊螺纹接头的密封能力取决于密封区域金属对金属密封的接触压力。为了保证密封能力，接触压力需大于油气的压力。利用解析方法评价特殊螺纹接头的密封能力，通常采用密封强度的概念，即密封面接触压力σc在有效密封长度L 上的积分。利用密封强度评价特殊螺纹接头的密封能力有实际意义，不仅在特殊螺纹接头设计开发过程中，可以作为一个评价标准对比分析，筛选出最优化的设计，并且还可以应用到整个扣型的产品线认证中，筛选出最差的公差配合形式，减少全尺寸实物试验的样品数量，节省大量的人力物力。

目前，大量研究工作集中于如何利用有限元分析定量的评价特殊螺纹接头的密封能力。Murtagian等［7］进行了相关实物试验，分别研究了有螺纹脂和无螺纹脂两种状态下密封面接触压力与密封能力之间的关系，提出了幂指数形式的密封强度Wa：

Murtagian 还给出了特殊螺纹接头保证密封能力的临界值Wac，当Wa∧Wac，表明接头具有足够的密封能力。Wac表达式如下：

式中 P —— 内压，MPa；

P标—— 标准大气压力，MPa；

B，m —— 拟合系数。

有螺纹脂和无螺纹脂两种情况下的Murtagian密封评价准则拟合系数见表1。

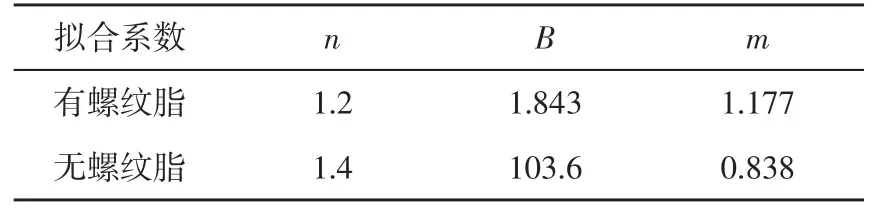
表1 Murtagian 密封评价准则拟合系数

但上述密封评价标准过于保守，原因是Murtagian 的试验基于泄漏速率Q 为0.025 cm3/15 min，而ISO 13679 ∶2019《石油天然气工业 套管及油管螺纹连接试验程序》中允许的最大泄漏速率为0.9 cm3/15 min；并且Murtagian 的试验是在室温条件下进行的，并未考虑到高温的影响。

针对以上两点，考虑到高温高压井接头破坏的实际情况，Xie 进一步提出了密封临界值Wac的修正表达式［8］：

随后Xie 等经过进一步的试验，又提出了针对热采井工况的密封评价准则［9］。此评价准则进一步引入泄漏速率及油套管尺寸的影响。在新的评价准则里，定义了两个变量SC和SO。

式中 D —— 管子直径，mm；

A，K —— 拟合系数。

SC可理解为密封能力，SO为实际工况对密封性能的要求。当SC≥SO，可认为接头的密封性能是足够的。文献［9］中给出了拟合系数值，见表2，当利用有限元进行分析，推荐使用极限值。

以上所述定量分析方法都还具有一定的局限性，可作为参考，但不能用作评价密封性的绝对标准［9］。

3 特殊螺纹接头抗疲劳性能

需要评估接头抗疲劳性能的钢管包括深海立管、热采井套管、水平井套管、钻井套管等［10-12］。接头可能发生疲劳破坏的位置有螺纹齿根、泄压槽、台肩等部位［13］，而交变的弯曲载荷是产生疲劳裂纹的主要来源。在上扣后或外部载荷作用下，接头局部位置已经发生了塑性变形，基于低应力幅的疲劳分析方法并不适用，而需要引入基于应变的疲劳分析方法。因为有限元分析结果可以提供模型的所有应力、应变信息，所以特别适用于疲劳分析。疲劳寿命的简单计算可采用Coffin-Mansion 关系式［14］：

表2 Xie 密封准则拟合系数

式中 Δε——应变幅；

Nf—— 疲劳寿命，次；

σf，εf，b，d —— 材料疲劳性能参数。

获取材料疲劳性能参数通常比较困难，需进行等应变下的低周疲劳试验，且试验过程较难控制。Baumel 和Seeger 给出了材料的疲劳性能参数的估算方法［15］。对于低合金钢，σf=1.5Rm，εf=0.59a（若Rm/E ∧0.003，a=1.0；否则a=1.375-125Rm/E），b=-0.087，d=-0.58。

4 分析结果与讨论

4.1 接头弯曲载荷下的应力分析

为验证有限元分析的正确性，对管体内表面弯曲产生的轴向应力与理论计算值进行了对比。根据ISO 13679 ∶2019 接头全尺寸评价试验标准，纯弯曲载荷下管体内表面产生的轴向应力σa可用公式（8）进行计算。对于所模拟工况，虽然为复合载荷，但上扣及内压载荷不会使套管上产生明显的轴向应力，其数值可忽略不计，所以公式依然适用。

式中 Dleg—— 狗腿度，即弯曲度，（°）/30 m；

t —— 壁厚，mm。

有限元计算弯曲产生轴向应力与理论值对比如图4 所示，二者基本一致，验证了模型的准确性。

图4 有限元计算弯曲产生轴向应力与理论值对比

图5 所示为接头在60°/30 m 弯曲度下的轴向应力云图。在弯曲载荷下，套管一侧承受拉应力，相对一侧承受压应力。应力集中区域位于不完整螺纹、接箍泄油槽以及台肩部位。图6 所示为接头在60°/30 m 弯曲度下的Mises 等效应力云图。最大等效应力位于倒数第二牙不完整啮合螺纹承载侧，应力值为1 030 MPa，已超过材料的屈服强度，产生明显的塑性变形。相对地，在压缩面上尾扣部位的导入侧为应力集中区域。通过对比不同弯曲度下不完整螺纹上的等效塑性应变发现，随着弯曲度的增加，塑性变形逐渐向内部扩展，尤其位于螺纹承载侧与齿底的过渡部分，成为塑性变形集中的区域，如图7 所示。局部塑性变形并不能影响整个接头的结构稳定性，弯曲载荷下接头的整体结构稳定，没有出现管体缩颈、屈曲、螺纹滑脱等现象。

图5 轴向应力分析结果

图6 Mises 等效应力分析结果

4.2 密封性能

图8 所示为密封强度的变化趋势曲线，随着弯曲度的增加，拉伸面的密封强度逐渐下降，而压缩面上的密封强度逐渐增加，二者的变化趋势基本呈线性关系。图9 所示为60°/30 m 弯曲度下的拉伸面和压缩面接触压力分布，当施加弯曲载荷，拉伸面和压缩面上的接触压力分布发生改变，拉伸面接触长度降低，接触压力下降，压缩面上则呈现相反的变化趋势。因此，在进行具体工况载荷下的密封性能分析时要综合考虑两方面的影响。

图7 不完整螺纹上等效塑性应变随弯曲度变化曲线

图8 密封强度变化曲线

图9 密封面接触压力对比

图10 所示为弯曲及内压载荷下密封能力的计算结果，按照Xie 提出的密封准则，对内压及不同弯曲度下密封面的密封能力进行定量计算，按照公式计算出120.7 MPa 内压、0.9 cm3/min 泄漏速率下的SO值为49.65 m·MPa1.557。如图10 所示，拉伸面和压缩面上的SC值都大于密封需求SO值1 倍以上。因此，接头有很大概率可以保证密封性能。

4.3 疲劳寿命的评估

图10 弯曲及内压载荷下密封能力的计算

明显的疲劳破坏通常位于接头上高应力应变状态的区域。利用Coffin-Mansion 公式对不同弯曲度下的接头危险区域的疲劳寿命进行了估算。如图11 所示，整体来看，接头的抗疲劳性能良好，能够满足设计及使用要求；另一方面，可以看到，随着弯曲度的增加，疲劳寿命随之降低。其中最危险区域位于接箍泄压槽处，此处也是接头上传统意义上的危险截面。但泄压槽处的疲劳寿命相对于螺纹及台肩部位，对于弯曲载荷的敏感度相对较低。

图11 疲劳寿命随弯曲度变化曲线

5 结 论

（1） 弯曲载荷下，特殊螺纹接头应力分布不均，存在应力集中区域。套管管体一侧承受拉应力，相对侧承受压应力。随着弯曲度的增加，外螺纹最后4 牙不完整螺纹的齿侧塑性变形逐渐增大，并逐渐向内部扩展。

（2） 弯曲载荷下，密封面上存在不同的接触压力大小及分布，评价接头密封性时应分别对两侧的密封强度进行评估。随着弯曲度的增加，拉伸面的接触压力下降、接触长度降低，压缩面的接触压力升高、接触长度增加。定量分析表明，此规格TPG2 HC 特殊螺纹具有优异的密封性能。

（3） 随着弯曲度的增加，接头的疲劳寿命逐渐降低，对于所分析接头，发生疲劳破坏最危险区域位于接箍泄压槽处。