数学课堂中基于深度学习的核心问题设计
李衡
数学核心素养的形成离不开特定的数学活动。传统的师生一问一答、死记硬背、题海战术的学习方式,无法实现学生学习的主动参与、思维的深度发展,更谈不上数学核心素养的形成。在具体问题情境中的深度学习,强调学生问题的生成、知识结构的整合、深度的理解、思想方法的迁移和应用,以此逐步形成核心素养所强调的必备品格和关键能力。课堂教学中,核心问题对驱动深度学习有着重要意义。围绕着深度学习的展开,教师把握核心问题的内涵意义、结构特征、实践策略,让学生的深度学习真正发生,是培养学生数学核心素养的重要途径。为此,教师要通过设计核心问题,引领学生达成深度学习。
一、把握核心问题的内涵意义,让深度学习具有动力
深度学习指的是基于理解的学习。深度学习关注学生参与学习的动机,关注学生在活动过程中的理解建构,关注学生在思考过程中的迁移和应用。深度学习离不开学习情感的积极支持与思维的剧烈碰撞,而问题是数学思考的“引擎”,因此学生的深度学习特别需要核心问题的引领与驱动。上海市特级教师潘小明对核心问题的定义是:基于课时核心知识和学生的认知水平,关注数学核心素养,引领课堂教学情境性的问题。教师明晰核心问题的内涵和意义,有利于改进教学设计,增强学生深度学习的主动性。
(一)核心问题可激发学生参与学习的积极性
新课程背景下,数学课堂教学应以问题为开始,以解决核心问题为主要任务。核心问题的产生应源自学生提出的问题,然后师生一起把这些问题梳理并进一步凝练、升华,形成核心问题。因为问题源自学生,他们在数学学习时就不会再“被牵着鼻子走”,学生解决问题的主动性就会增强。由于问题是学生提出的,比较接近学生的“最近发展区”,因此学生对问题的理解与探索相对容易,只要“跳一跳”就可以解决问题。这样,学习过程既有挑战性,学生又能较为轻易地克服遇到的困难,从而激发了学生解决问题的积极性。
(二)核心问题可发展学生的数学思维
深度学习的本质是实现深度思维。核心问题统领若干个相关联的小问题形成“问题串”,学生在学习过程中围绕“问题串”展开探究活动,这样“问题串”就转化成了“活动串”。在体验活动的过程中,学生的学习活动在“问题串”的引导下层层深入,又构成了一条思维深度发展的“思维串”。深度学习就是借助“问题串”展开体验活动并发展学生的深度思维。
(三)核心问题可提升学生的数学素养
学生进行数学学习不应仅仅是学到知识,更多的应是通过学习活动提升学习能力和端正学习态度。核心问题统领下的课堂教学是以学生小组合作学习方式进行的,在这个过程中,需要学生思考、倾听、表达等学习能力的参与,同时通过同学之间的互动,学生的情感、态度和价值观也得到了提升。
二、遵循核心问题的设计原则,让深度学习有路径可寻
核心问题是引领数学课堂深度学习的原动力和牵引力,核心问题与相关联的小问题构成了“问题串”,遵循特定原则,把学术形态的教学内容转变成教育形态的问题研究。核心问题引发深度學习要突出以下四个原则。
(一)可及性和挑战性原则
核心问题的深度、难度、广度要与学生的知识和能力水平相适应。核心问题的提出要符合学生的学习规律和当下的认知水平,教师应找到学生的“最近发展区”,以此来设置核心问题。这样,学生既能够在力所能及的范围内探究和解决问题,又能够避免因为问题过偏、过难而丧失对数学学习的兴趣。此外,核心问题的设计也不能一成不变,对学生没有任何挑战。教师要根据学情,设计能让学生“跳一跳够得着”的核心问题,引领学生走向深度学习,发展学生的数学思维。
(二)典型性和针对性原则
核心问题的设计应符合数学学科本身的知识特点和学习规律,具备典型的数学特征。问题设计不能盲目追求调动学生的学习兴趣,不能脱离数学知识本身,也不能脱离学生的实际数学学习情境。此外,核心问题也要有针对性,应设计在重要数学概念及数学规律的理解、分析之处,要通过核心问题使学生形成处理问题的典型思路、方法,了解知识间的内在联系以及易错、易混的问题等。教师要抓住学生理解和应用知识的关键处来提出核心问题,使教学击中要害,培养和发展学生的分析能力和综合能力。
(三)具体性和探究性原则
教师设计的核心问题应明确而具体,简单而有效,其内容不能过于宽泛,那样会分散学生的精力,使学生抓不住问题的本质,甚至会因为一些无效的问题环节使学生走向问题解决的反方向,浪费宝贵的教学时间,降低教学效率。此外,教师还要通过设计核心问题来引领学生去探究。在问题提出的过程中,教师可以设置悬念,揭示矛盾,从而激发学生主动探究的欲望,引导他们积极参与,在探究中获取新知。
(四)程序性和启发性原则
程序性指的是核心问题的解决过程要与学生数学思维发展的顺序一致。教师设计的核心问题要有利于启发学生的逻辑思维,使学生把握住核心问题的实质。程序过于精细,核心问题的环节过于显露,引不起争论,不利于学生思维的展开;程序粗放,隐含条件太多、太隐蔽,学生不容易抓住要领,也会使关于核心问题的对话交流无法深入开展。此外,核心问题的设计还要有启发性,要启发学生通过理解和解决问题,逐渐深度思考,形成自己的数学思维。
三、形成核心问题的实践策略,让深度学习真实发生
课堂教学要以核心问题的提出作为教学的起点,以在教学过程中解决问题作为主要任务。教师要组织学生根据问题开展自主学习、动手操作、小组讨论、集体交流、问题再生成等学习活动,完成解决问题的过程。
(一)围绕教材内容设计核心问题
核心问题指向的应该是数学知识的核心内容,所以,教师要深入分析教材,理解教材的核心内容,把握知识的本质,从而设计出高质量的核心问题。
1.围绕概念关键词设计核心问题
数学概念具有高度的概括性,概念中的关键词更是浓缩的精华,教师理解好关键词,就能提纲挈领地帮助学生理解概念。如教学“周长的认识”时,周长的概念为“封闭图形一周的长度,是它的周长。”学生对于关键词“一周”的理解,认为就是“一圈”的意思,这是用生活语言来解释。但是,教师如果仅止步于此,学生的理解就不够深刻,教师应该更进一步,设计核心问题:“一周”是什么意思?你能结合图形边比划边说吗?从而让学生明晰“一周是从起点回到起点,一周与方向、起点无关”。理解了这个意义,学生也就能明白,周长之所以是封闭图形,是因为只有封闭图形才能从起点又回到起点。所以,本节课应围绕核心问题“一周是什么意思”展开教学活动。
2.围绕概念的形成设计核心问题
有的概念看似很简单,学生很容易学明白,但越是简单就越容易出现理解偏差。学习概念时,学生只有深入地感知其形成过程,逐步建构其形成表象,才能在未来的学习中使其得到正确地拓展和提升。 如教学“长方体和正方体的认识”一课,如何让学生理解长、宽、高对于长方体的重要性呢?在教学中,教师可把“长、宽、高有什么意义”作为核心问题展开教学活动,通过一“搭”一“拆”,让学生经历“长、宽、高决定长方体的大小”这一核心概念的形成过程。学生先选择12根小棒搭一个长方体的框架,教师相机提问题:“如果拆掉其中的一条棱,你能比划出它的大小吗?”“还能再拆掉一些棱吗?至少要剩下几条棱才能还原这个长方体的大小呢?”教师放手让学生自主探索实验、讨论交流,学生得出结论:至少要剩下相交于一个顶点的三条棱。学生认为,因为长方体相对的四条棱长度相等,共有三组,通过余下这一组的三条棱就可以还原每组其余的三条棱。教师并没有停下而是继续去掉高,只剩下长和宽,学生发现,此时只能确定一个面,无法知道这个长方体有多高。教师再去掉长、宽,学生得出,只知道长方体的高,无法确定长方体的面。最后,教师提出核心问题:长、宽、高的意义是什么?从这个探索活动中,学生悟出:长、宽、高决定一个长方体的大小,它们对于长方体有着至关重要的意义。
3.围绕概念的关联设计核心问题
数学知识之间有其内在的联系,知识点分散到每节课的问题中时虽然不一样,但是其本质相同,因此其核心问题往往是一样的。由于这些问题之间属于平行关系,所以我们应该整合相关联的内容,提炼出核心问题,使学生达到对知识的整体理解。如“商中间、末尾有零的除法”一课中有3个例题:309÷3=103、420÷3=140、832÷4=208。很多教师往往分散进行教学,先让学生感受被除数有零、商有零,再感受被除数没有零、商有零的情况。这3个例题有其不同点,但本质是一样的,都是因为“被除数某位除以除数不够商1”。所以,写零与被除数是否有零没有直接的关系。因此,教师可提炼出其核心问题:商中为什么写零?教师可以把这3个例题整合在一节课中进行教学,让学生感受“零的产生并不是因为被除数中有零”的原因,从而让学生对算理的理解更加深刻、到位。
(二)根据学情设计核心问题
教师设计的问题要接近学生的“最近发展区”才有利于解决,所以,教师要关注学情,因为学生的错误点和困惑点就是解决问题的关键。以此来设计核心问题,往往能起到事半功倍的作用。
1.在错误资源中生成核心问题
没有无缘无故的错误,学生的每一次错误都应引起教师的反思。尤其是出错率较高的地方,往往正是学生最难理解之处,解决了这个错误,就能加深学生对新知的理解。如教学“乘法分配律”一课,学生在运用规律进行简便计算时出错率相当高,常犯的错误是相同因数只乘了一次,即(120+30)×6=120×6+30。教师反复强调,可是强调多了学生又与乘法结合律混淆,出现如(120×30)×6=120×6×30×6这样的错误。为什么会产生这样的错误呢?我发现,问题都指向学生对乘法分配律中算式两边“6”的意义没有理解好,所以学生对规律的运用生搬硬套。当学生提出“为什么左边的算式只有一个6,右边的算式却要写两个6呢”这个核心问题时,根据规律形成的特点,我拟定了“数、事、形、理”的“问题串”。“数”是根据例题引导学生发现(120+30)×6与120×6+30×6的区别,教师提出问题:“观察这两个算式有什么规律?”通过观察,学生初步建立起乘法分配律的模型。“事”是把规律还原到生活中,教师提出问题:“生活中还能举出这样的例子吗?”用生活的例子来解释数学模型,能帮助学生深刻地理解抽象模型的内涵。“形”是学生根据自己举出的例子抽象出模型,教师提出问题:“这些例子能用算式来表示吗?”通过大量的算式,学生加深了对乘法分配律算式模型建立的印象。“理”就是理解乘法分配律的算理,也就是学生提出的核心问题:“为什么左边的算式只有1个6,右边的算式却要写2个6呢?”经过大量生活实例的铺垫,学生很快就找到了答案:“这3个‘6’的意义不同,左边算式表示6套衣服,分配到右边变成是6件上衣加6条裤子,如果右边少了1个6,那就只有6件上衣和1条裤子,只能凑成1套,凑不成6套衣服了。”看似复杂的概念,学生借助“6条、6件、6套”这3个数量轻轻松松就“搞定”,而且学生还进一步认识了乘法分配律的内在含义。这样,就比单纯从算式意义上来理解或通过公式的记忆顺畅多了,使看似复杂的问题变得简单易懂了。
2.在学生困惑处生成核心问题
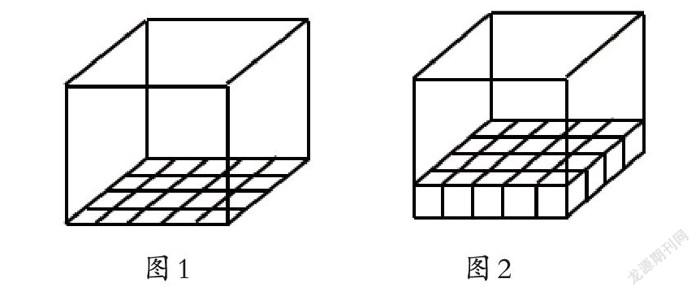
从一定意义上来说,教学的过程也是一个解惑的过程,学生的疑问之处正是教学中最值得探究的地方。教师要分析学生形成困惑的原因,追根溯源,找出核心问题。如在教学“长方体的体积”一课中,当学生得出长方体的体积=长×宽×高时,再通过底面积=长×宽,又可引导出长方体的体积=底面积×高。我们通常都认为这个推导合情合理,可是学生却有疑问:“底面积×高为什么会得到体积呢?体积怎么会跟底面积有关系呢?”这些疑问提醒我们要找准核心问题的实质:体积公式的意义,即长×宽、宽×高、长×高分别得到什么?是面积吗?这里的关键是引导学生分步观察,长×宽得到底面积为20 m2(如图1),通过底面积我们可以想像出第一层的体积是20 m3(如图2)。
高是几就有这样的几层,所以长×宽既可以表示底面积,也可以表示第一层的体积,于是用底面积×高可以得到长方体体积。有的学生还能从正面看,用正面的面积×宽也能求出体积;还可以从侧面看,横截面的面积×长也可以求出体积。对长方体体积公式深入理解之后,在教学“圆柱体的体积”时,学生的思考方式就会更加便捷,他们不用经历把圆柱转化成长方体的全过程,而是想到算出底面积是多少,就可以知道第一层的体积是多少,高是几就有这样的几层,直接用底面积×高,完美地实现了体积计算的迁移。
(三)把握数学思想设计核心问题
数学学科核心素养的培育离不开数学思想方法的渗透。学生只有掌握了解决问题的一般性思维策略,才能有效地解决具体问题。教师要善于挖掘教材中所蕴涵的数学思想和方法并渗透在教学中,引导学生去感悟和體验。
如教学“数字编码”时,很多教师设计的教学重点是让学生了解编码中每个数字所蕴涵的意义,而这不是编码学习的数学价值。教师要把重点放在让学生感受编码的神奇上,使学生体会编码的唯一性。所以,本节课应根据唯一性这个数学思想方法来设计核心问题:全国14亿人口的身份证号码会重复吗?刚开始,很多学生认为一定会重复。接着,教师通过一个具体的身份证号码,结合政区图让学生展开探索活动:35代表福建省,福建省有3689万人口,说明只有3689万人的身份证前两位是一样的。01代表福州市,福州市有589万人,说明只有589万人的身份证前四位是一样的。81代表福清市,福清市有139万人口,说明只有139万人的身份证前6位是一样的。根据出生年月日,福清市同年同月同日出生的人大约有437人,说明只有437个人的身份证前14位可能重复。通过三位的顺序号可以把437个人的身份证号依次排列。所以,身份证号码不会重复。通过这个过程,学生感到很神奇:14亿人口居然能做到身份证不重复!这充分体现了数字编码的唯一性。理解编码的数学思想方法之后,学生在编学号的时候就会考虑如何提供有效信息让学号不重复。
基于学生深度学习来设计核心问题,实现了数学学习从知识记忆转变为问题解决,促进了深度学习的发生和发展。
(责任编辑:杨强)

