树的k-距离染色
2022-06-28 03:13:42陈海钰
兰州职业技术学院学报 2022年3期
陈海钰
(兰州职业技术学院 经济管理系, 甘肃 兰州 730000)
1.引言

约定:本文主要研究的树T是除了悬挂点之外每一个点的度都达到最大度Δ(≥3)(因为最大度为Δ的树都是该树的子树),且d(T)≥k(d(T)表示T的直径,如果d(T) 对图G(V,E),令: 定理1设T是最大度为Δ的树,且满足上述约定,则 (其中l=0,1,2,…). 证明: 当k=2l时,存在v∈V(T)使得|Bl[v]|=p,所以χk(T)≥p.为证明χk(T)≤p,下面用贪婪算法给出T的用了p种颜色的k-距离染色c: 当k=2l+1时,存在u0,u1∈V(T)使得|Bl[u0]∪Bl[u1]|=q,显然,∀u,v∈Bl[u0]∪Bl[u1],有d(u,v)≤2l+1.所以χk(T)≥q.为证明χk(T)≤q,下面用贪婪算法给出T的用了q种颜色的k-距离染色c: 图中的v0 与 综上,此染色方案可以使树T有q种色的k-距离染色. 推论1[6]T是树,则χ(T)=2. 证明:定理1中取k=1即得结论. 推论2[7]若T是最大度为Δ的树,则χ2(T)=Δ+1. 证明:定理1中取k=2即得结论.2. 主要结果

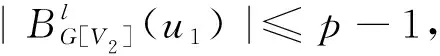
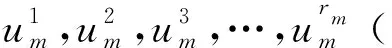


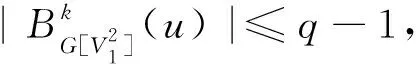


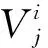
猜你喜欢
黄河之声(2021年8期)2021-07-23 03:34:32
成都中医药大学学报(教育科学版)(2021年1期)2021-07-22 07:29:52
中国石油石化(2021年10期)2021-07-16 07:31:28
当代音乐(2020年10期)2020-10-26 18:34:52
学生天地(2020年19期)2020-06-01 02:11:36
孩子(2019年10期)2019-11-22 08:06:01
销售与市场·渠道版(2019年2期)2019-03-28 03:51:40
漯河职业技术学院学报(2017年4期)2017-08-07 08:45:53
科技视界(2014年10期)2014-02-24 08:31:20
娃娃画报(2009年11期)2009-12-07 03:38:20

