直线光栅伺服系统自抗扰控制仿真分析与实验研究
黄小津,胡超迪,魏 巍,李加胜
(1.机械制造工艺研究所中国工程物理研究院,四川 绵阳 621900)(2.上海交通大学机械与动力工程学院,上海 200240)
1 引言
在工程实际中,往往可以通过消除误差来实现系统的控制,而其中的一个关键问题是采用何种方式抑制各种不确定的外部扰动对系统控制的影响。PID控制的核心思想是基于误差的反馈控制,控制算法将输出信号采集,并与输入信号作差,然后将该误差作比例、积分、微分后进行线性相加组合,得到被控对象的控制信号。
文献[1]提出了基于PID进行改进和创新的自抗扰控制技术,它继承了PID控制的主要思想,即状态误差反馈,又克服了其系统快速响应与容易产生超调之间的矛盾,并拥有线性误差反馈所不具有的特点,更具有其独有的扰动估计补偿的核心思想。自抗扰控制方法提出后,已经有众多的学者、工程师展开了大量的理论研究与工程应用。
文献[2]根据Lyapunov 函数思想研究了扩张状态观测器(ESO)的误差,并列出提高其估量精度的参数所应满足的条件,研究了存在干扰条件下系统稳态误差的范围以及在无干扰条件下稳定的充分条件。
文献[3-4]深入研究了不同非线性因素下自抗扰控制系统的收敛性,分别基于单输入单输出和多输入多输出非线性系统进一步证明了在闭环条件下的收敛程度。文献[5-6]详细分析了描述函数法对包含非线性自抗扰控制系统的极限环。文献[7-9]分析研究了Lyapunov稳定性、绝对稳定性以及描述函数法的极限环对自抗扰控制系统稳定性的影响。目前,自抗扰控制技术已经在控制领域,特别是针对一些拥有非线性,大扰动,模型不确定等特性的控制系统,有了大量的研究与应用。文献[10]研究了自抗扰控制技术在冷轧生产过程中的应用。文献[11]研究了自抗扰控制技术在微机电换能器上的应用。文献[12]研究了自抗扰控制策略的球磨机制粉系统,通过理论与实验证明了自抗扰控制算法具有较好的抗干扰性以及鲁棒性。文献[13]研究了自抗扰控制技术在AUV航向控制中的应用。这类应用的特点是系统未知、为非线性、会受外扰等多种因素影响。
为直线伺服平台设计了自抗扰控制算法,通过数值仿真研究了该算法中一些参数对直线伺服平台控制性能的影响,比较了在系统中自抗扰控制算法与传统PID控制算法对阶跃响应以及常值干扰的控制效果。基于matlab仿真与实验,对比分析了自抗扰控制算法与PID控制算法抗干扰性能和优缺点。在自抗扰控制实验中,对直线伺服系统实现了模型辨识与自抗扰控制,观察自抗扰控制下的阶跃响应并在加入模拟常值干扰后观察系统响应,对自抗扰控制算法能迅速抑制干扰进行了研究。
2 自抗扰控制
对外部扰动进行估计并据此进行补偿是自抗扰控制原理的精髓所在。一般的自抗扰控制器的结构,如图1所示。自抗扰控制通常由四个部分组成:根据输入信号安排合适中间过程的过渡过程安排部分、可以估计系统状态并估计扰动的系统扩张状态观测部分、线性或者非线性的状态误差反馈部分和根据估计的扰动进行补偿的扰动估计补偿部分。
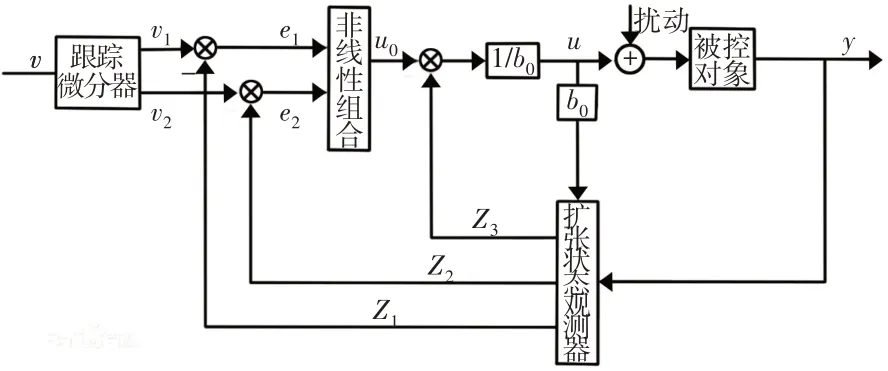
图1 自抗扰控制框图Fig.1 Block Diagram of ADRC
2.1 状态误差反馈
反馈机制是受控系统特征。反馈机制能在一定范围内使系统性能按人的意愿得到改善,负反馈机制还具有一定的抑制微小扰动的作用。由前文可知自抗扰控制器的状态误差反馈接收的误差是设定值的误差以及其微分的误差,相当于实现PD 控制。传统的线性PD控制的误差反馈律如下所示:

式中:u0—输出的控制量;e1、e2—控制量误差以及其微分误差;β1、β2—参数。
除了线性的状态误差反馈形式之外,还有很多非线性的形式可以采用,参考文献[1]对不同的非线性形式做了大量分析,证明适当的非线性反馈比线性反馈效率高很多。文献[6]提出了如下一些非线性形式的状态误差反馈:
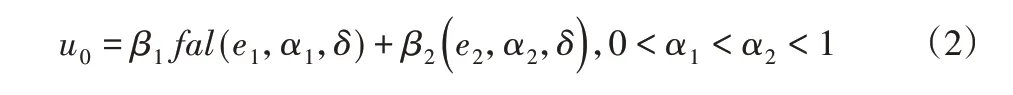

式中:α1、α2、β1、β2、δ、r、h1、c—参数;函数fal(e,α,δ)可表示成:
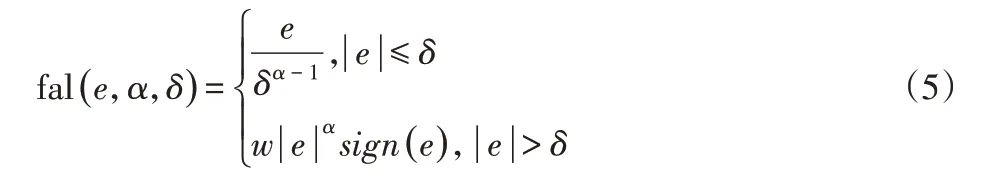
采用使用非线性反馈式(4)作为反馈控制律。
2.2 扩张状态观测器
在反馈控制系统中,负反馈对外界扰动有一定的抑制作用。而在自抗扰控制,就是利用扩张观测器通过系统的输入输出来对扰动进行精确的估计,根据扰动的估计值进行前馈补偿从而消除扰动影响的控制方法。
扩张状态观测器借用了状态观测器的思想,把能影响被控输出的扰动当作新的状态变量来观测,根据控制系统的输入与输出信息,估计出系统状态变量与这个新的状态变量。扩张状态观测器的结构图,如图2所示。
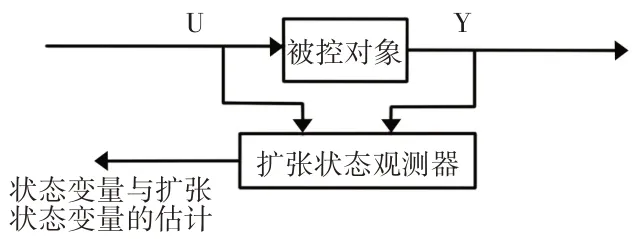
图2 扩张状态观测器框图Fig.2 Block Diagram of Expansion State Observer
对于如式(6)所示二阶系统,系统原有状态变量x1,x2,现将f(x1,x2)扩张为状变量x3,若设f(x1,x2)的导数为w(t),则扩张后的系统变成式(7)。

式中:x1,x2—系统状态变量;b—系统固有参数。

对于式(7)所示的状态方程,可建立如下离散形式的状态观测器,只要选择好参数,该观测器z1、z2、z3能很好地分别估计状态变量x1、x2、x3。
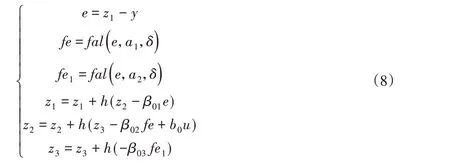
式中:δ、β01、β02、β03、a1、a2—参数。
关于这些参数的整定,参考文献[1]给出了说明,z3估计f(x1,x2)的误差,z2估计x2的误差,z1估计x1的误差的大小分别约为为f(x1,x2)的大小,可估计其最大值计算。那么只要取得β03足够小于w0,β02、β01取得足够小,理论上就能获得一个小的稳态估计误差。
3 自抗扰控制仿真分析
为说明自抗扰控制的优势,将模拟控制一个一维直线运动平台,对同一个二阶系统分别采取自抗扰控制和传统PID控制进行仿真。仿真中调整自抗扰控制中各项参数如下:
1.r0=1e6;h0=5e-4;%安排过渡过程参数;
2.r1=0.5/h^2;h1=5*h;c=0.05;%非线性组合参数;
3.β01=1/h;β02=3.3e-1/h^2;β03=1e-3/h^3;δ=h;a1=1;a2=1;
%扩张状态观测器参数;
4.b0=1e7;%扰动补偿参数;
5.k=1e7;b=100;a=50;%二阶系统参数。
仿真中调整PID控制中各项参数如下:
1.P=5e-5;2.I=2.5e-9;3.D=1e-5。
3.1 阶跃响应分析比较
两种控制方法有相似的位移曲线,如图3所示。在当前参数下,两者都没有超调,且两者过渡时间相近。可以发现,PID控制的响应在该参数下较快,但随着稳态误差的减小,纠正速度逐渐降低,最终达到接近稳定的状态反而没有自抗扰控制快。自抗扰控制的相应曲线上看,该曲线几乎以直线靠近阶跃输入设定值,快速的同时没有超调。事实上,可以比较两种控制的速度变化曲线来更细致地分析。两种控制方法的速度曲线,如图4所示。
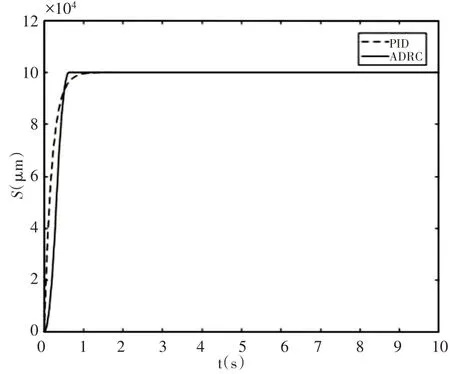
图3 PID与ADRC的阶跃响应Fig.3 Step Response of PID and ADRC
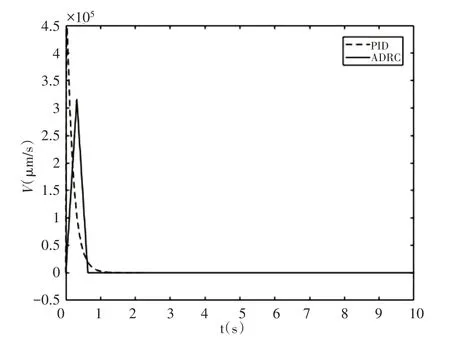
图4 ADRC和PID阶跃响应的速度Fig.4 Velocity of the Step Response of ADRC and PID
可以看出,PID方法的速度一开始产生了较大的跳变,这种跳变是不合理的,可能会对运动系统造成影响或者较大的速度超出系统能达到的范围。而图4中自抗扰控制方法的速度曲线在初始时基本上呈现等边三角的形状,这是受到安排过渡过程的作用形成的设定速度曲线,相比PID控制可以看出其最大速度更小。因而可以认为自抗扰控制的响应轨线比传统PID控制更合理。
3.2 抗干扰能力分析比较
自抗扰控制的核心内容和优势所在是控制方法的中的干扰估计和补偿,对自抗扰控制和PID控制抗干扰能力的分析比较可以说明其抗干扰能力的强大。
仿真将在第5s时两种控制方法下所控制的二阶系统的输入值中增加幅值不同的常值干扰和低频正弦干扰,观察两种控制方法下的最终输出响应来比较其抗干扰能力。
在第5s时加入常值干扰后两种控制方法下系统的输出,如图5所示。加入的干扰值为1V、0.5V、0.1V,图中可以看出,PID控制对常值干扰是有一定的抑制作用,但是抑制作用很差,恢复时间已经基本超出了图中5s的范围。而在干扰小于1V的范围内,自抗扰控制的输出基本不受干扰的影响,在图中已经无法看出。在加大干扰后,自抗扰控制的输出,如图6所示。
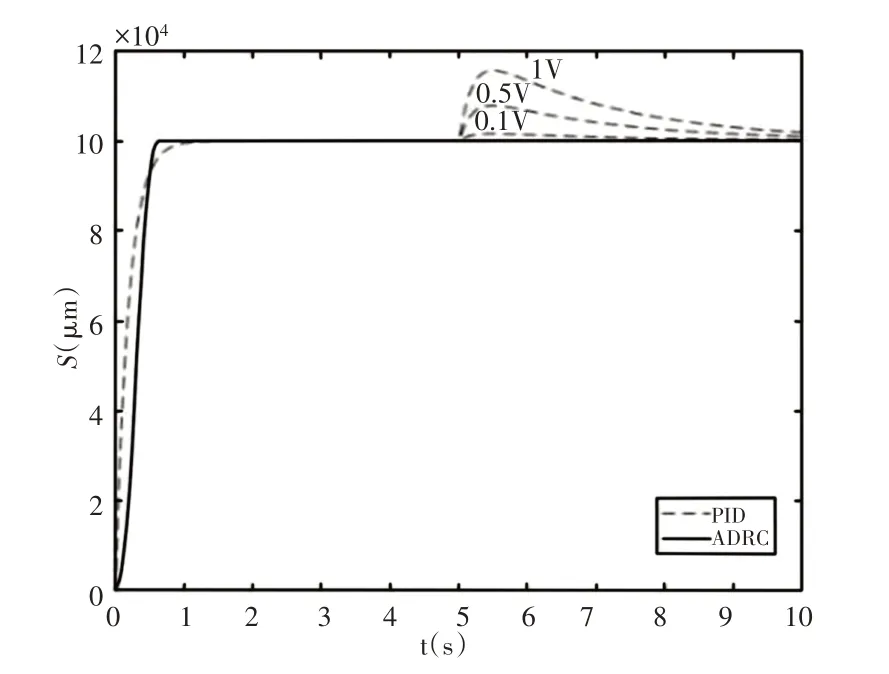
图5 ADRC与PID常值扰动下的响应Fig.5 Response of ADRC and PID with Constant Disturbance
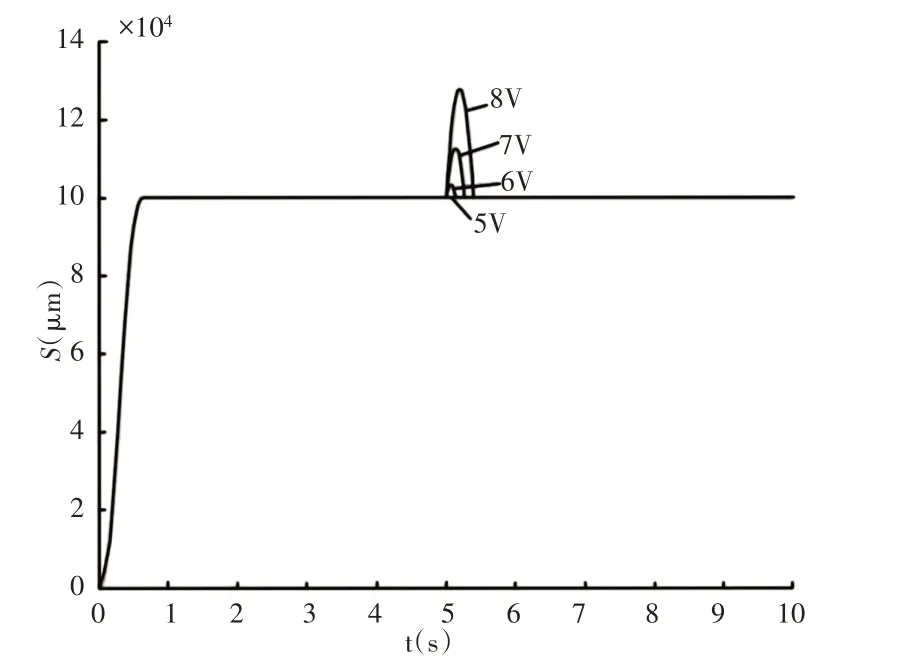
图6 ADRC更大常值扰动下的响应Fig.6 Response of ADRC with Lager Constant Disturbance
系统的输出在5V干扰下仍未产生明显的影响,在干扰继续增大后才产生比较明显的影响,但在干扰量为8V的作用下时,系统恢复设定值的时间约为0.5s左右,比图4中PID控制的恢复时间短很多。因此,从可控干扰的大小和恢复跟踪设定值的时间上来看,自抗扰控制比PID控制都有较大优势。
自抗扰的参数较多,过大或过小的参数选择会引起系统不稳定、产生超调或者响应、抗干扰能力减弱等情况。但很多参数的选择范围都比较大,整定较为容易,可以根据文献[1]建议的参数做适当调整来确定参数。
4 自抗扰控制实验
选用的直线运动平台设计,如图7所示。主要包含:直线电机、大理石底座、气浮轴承及平台导轨、光栅等。整个运动平台将被置于一气浮隔振台上,以减小环境振动的影响。

图7 直线运动平台实物图Fig.7 Picture of Linear Motion Platform
4.1 伺服系统辨识
伺服系统的辨识能了解系统特性,以更好地控制系统,在之后自抗扰控制中也可以根据辨识所得的系统选择合适的参数。为辨识该二阶系统,实验输入3 V的常值控制信号,通过NI Compact测量系统记录系统输入与同步的系统开环输出,即系统的阶跃响应。系统输出,如图8所示。
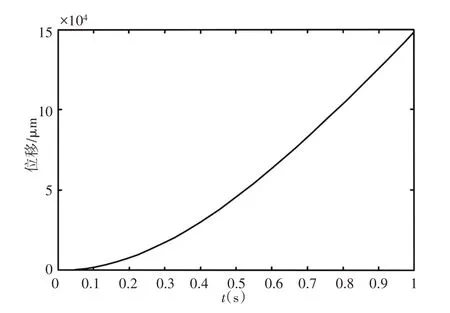
图8 系统阶跃响应Fig.8 Step Response of the System
利用matlab系统辨识工具箱对改输出与3 V常值输入进行传递函数辨识,模型为2极点0零点,得传递函数如下式(9)所示,拟合度达到了99.85%,可以认为建模与辨识是准确的。
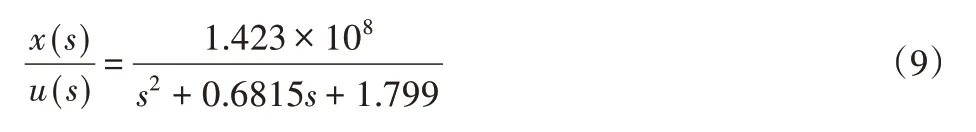
3.2 实验结果
自抗扰算法参数选择文献[1],针对二阶系统提出的参数做了微调,其中b0为1.423×108,状态非线性反馈参数中,为了减小位置误差,参数C减小2个量级。在实验参数的自抗扰控制下,伺服系统的105μm阶跃响应,如图9所示。系统响应与仿真结果基本符合,在该参数下略有超调。基本稳定后存在噪声和震荡,稳定后的截取一秒内的误差,如图10所示,均方根值较大,达到了0.5μm。
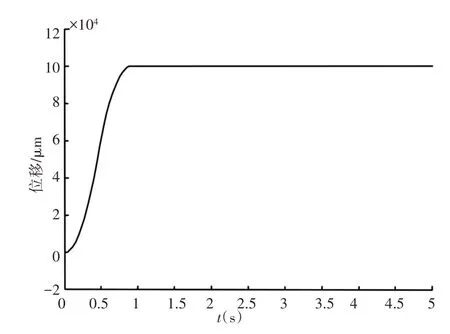
图9 伺服系统阶跃响应Fig.9 Step Response of the Servo System
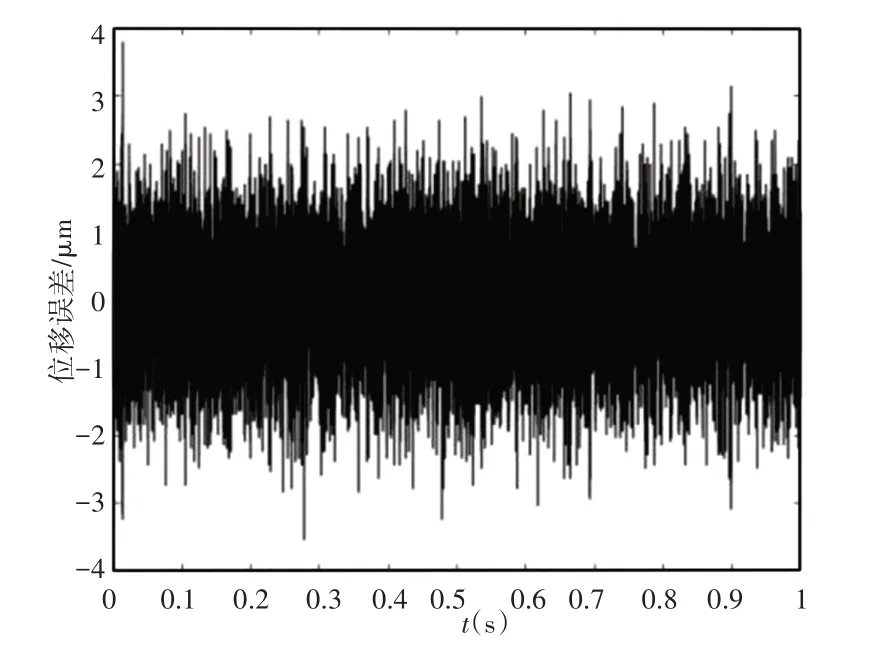
图10 稳定后的误差Fig.10 Error After Being Stable
实验中,使用模拟添加常值干扰的方式,干扰常值分别是0.1 V、2 V,结果如图11、图12所示。
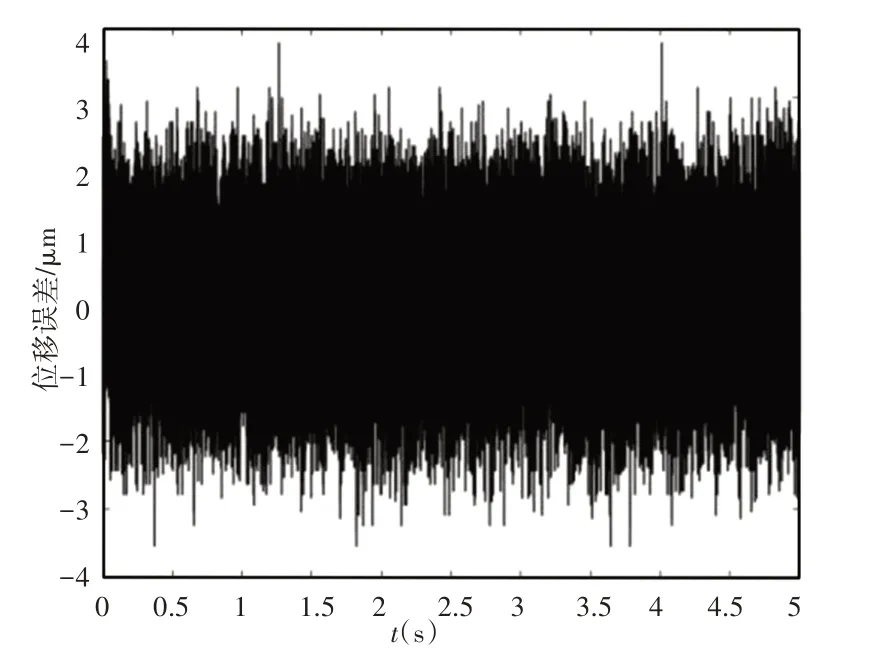
图11 0.1V常值扰动下响应Fig.11 Response of 0.1V Constant Disturbance
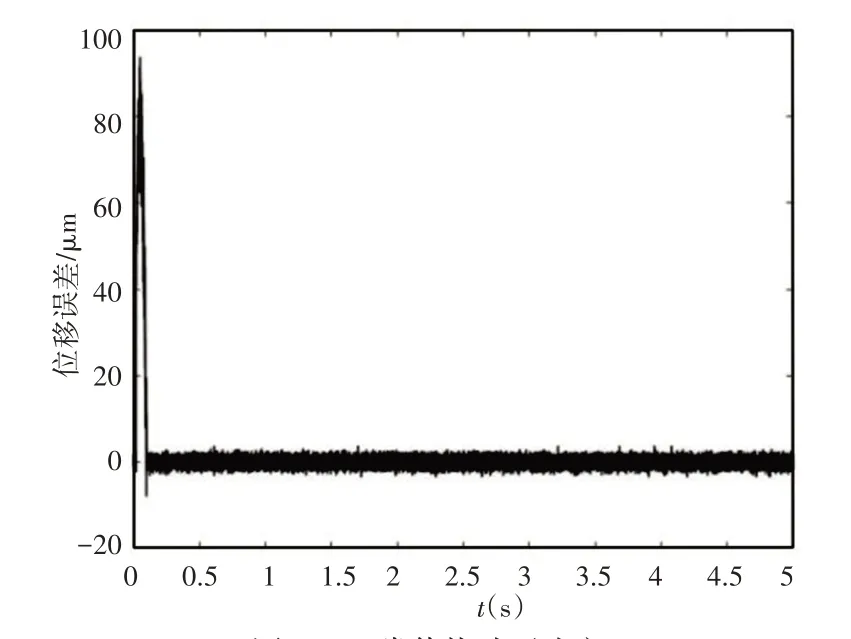
图12 2V常值扰动下响应Fig.12 Response of 2V Constant Disturbance
图中0时刻为扰动加入时刻。图中可以看出,在0.1V时几乎看不出影响,一方面也是因为噪声过大。在2V时,可以看出出现一个尖峰,随后回到稳定状态,所用时间分别为0.1s左右,产生的最大偏差为20μm、95μm左右。可以看出,自抗扰控制具有对常值扰动的抑制作用,扰动越大,误差变动越大与恢复时间越久。
5 结论
针对直线伺服平台二阶系统设计了自抗扰控制算法,基于基本的自抗扰控制算法,采用了最速控制综合函数形式的非线性状态误差反馈;扩张状态观测器的系统输入为控制器直接输出,即最后将系统转化为积分串联型。根据Matlab仿真结果,通过与PID控制算法比较来验证自抗扰算法的可行性和优势,比较包含了阶跃响应和常值干扰影响下系统的性能,自抗扰控制对比PID控制有如下优势:对阶跃响应能平衡快速响应与无超调,对常值扰动的抑制能力明显更强。在自抗扰控制实验中,对直线伺服系统实现了模型辨识与自抗扰控制,观察了自抗扰控制下的阶跃响应并在加入模拟常值干扰后观察了系统响应,结果显示。自抗扰控制能迅速抑制干扰作用。

