人体不对称运动在多因素干扰下稳定性研究

郭占腾，樊 军

（新疆大学机械工程学院，新疆 乌鲁木齐 830047）

1 引言

人体在多因素影响下的运动稳定性问题一直是人机工程、医疗器具、体育运动以及穿戴式机器人等领域的重点研究内容[1]。尤其是目前下肢外骨骼、智能假肢等高智能机器人正逐步被大规模的应用到军事、工业、医疗、虚拟现实等领域，这些穿戴品必然会对人体运动产生多方面的影响[2]。人体在多因素干扰下不对称运动稳定性变化的研究是这些穿戴设备与人体良好交互的基础。

目前国内外在这方面的研究主要分为两方面。（一）在人体运动研究方面，文献[3]人以人体行走为例，对膝关节进行运动学与动力学分析，得到膝关节各种运动参数的变化情况，为下肢运动提供了一定的理论基础；文献[4]通过点云采样技术拟合获得人体运动信息，实现了人体不对称运动信息有效提取，提高了人体运动识别的真确率；文献[5]通过传感器来获取肢体的实时姿态信息，设计了一种人体可穿戴式的人体运动捕捉系统；文献[6]通过建立一种能够实时反应人体运动特征的简化人体模型来研究人体运动。（二）在多因素干扰下人体运动稳定性方面，文献[7]进行了考虑外界干扰的拟人机器人模型的稳定性分析，给出了支撑多边形的计算机表达方法和失稳时旋转边界自动确定方法；文献[8]通过CGA（clinical gait analysis）以及动力学分析得到各关节驱动力矩并以此判断蹲起运动的稳定性。

以上各位学者分别对不对称的人体运动以及受到干扰外力时的人体运动稳定性采用多种方法进行研究，但是在实际情况下人体不对称运动的稳定性会受多种因素影响，不能只考虑单一因素。目前尚未见到将人体不对称运动与多因素影响结合到一起分析研究的案例。

因此针对不对称运动在多因素干扰下的稳定性研究，选取了人体蹲起这一极具代表性的运动做为研究案例进行研究。这种人体不对称运动是人们在日常生活中最常见的一种运动方式，在运动过程中速度、稳定性等时刻在变化，尤其是在搬运物体时，人体稳定性会受到负重、上身晃动以及外力干扰的影响，若运动的稳定性过低则会给人体带来不良后果。所以结合蹲起运动的运动学特点，通过提出三种性能因子来为人体蹲起运动稳定性的实时变化提供评价标准。

首先建立人体简化模型，对人体简化模型进行运动学、动力学分析，根据蹲起过程中受力及运动情况，分别设定了负重载荷因子、干扰外力因子以及上身姿态因子来综合判断单膝蹲起过程中的稳定性。最后通过实例计算及仿真验证该理论的正确性，该方法可以准确判断蹲起运动中稳定性的变化，为人体运动、拟人机器人或者助力外骨骼运动稳定性的研究提供理论依据。

2 构造人体简化模型

人体在蹲起过程中主要依靠髋关节、膝关节与踝关节的运动实现，所以为了方便计算，可以忽略头部、手部及脚部的运动，故将人体简化为5连杆刚体模型以便计算[9]。

3 蹲起过程稳定性分析

蹲起时，膝关节为主要运动及驱动关节，当人体负重过大时，人体在起身过程中膝关节提供的力就必须要随之增大，此时会导致蹲起运动过程的不稳定。

当人体在蹲起过程中受到外力干扰时，当外力较小时不会破坏该过程的稳定性，但是当外力过大时就会影响该过程。所以要保证蹲起过程的稳定性就要将外力控制在一个合理的范围内。人体在起身过程中若上半身发生X、Y方向的晃动时，特别是身体左右晃动时，会严重影响蹲起过程的平衡性从而导致失稳。

3.1 上身负重载荷性能因子

人体在进行单膝蹲起运动时，其下肢可分为支撑侧与摆动侧。向前跨步的腿为支撑侧，主要起支持身体与助人起立的作用；后者为摆动侧，主要起协调人体平衡的作用。

支撑侧膝关节水平加速度αx与垂直加速度αz

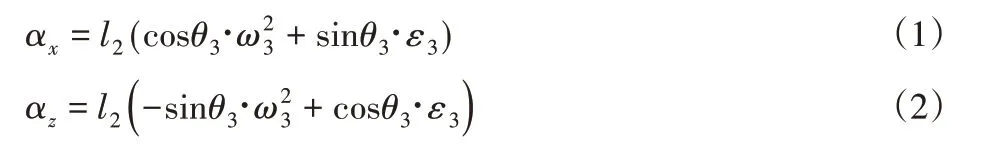
在摆动侧中由于膝关节是在绕该侧髋关节运动，在该侧中有相对运动，但是由于支撑侧膝关节提供主要力矩带动摆动侧完成运动，所以在摆动侧中，膝关节与支撑侧膝关节有牵连运动。根据刚体平面运动基点法将相对运动与牵连运动合成得到摆动侧膝关节运动。基点速度合成可表示为：

式中：ve—基于动坐标系的牵连运动；vr—B的相对运动。两者都可以分解到X轴与Z轴上。

牵连运动速度水平速度与垂直速度：

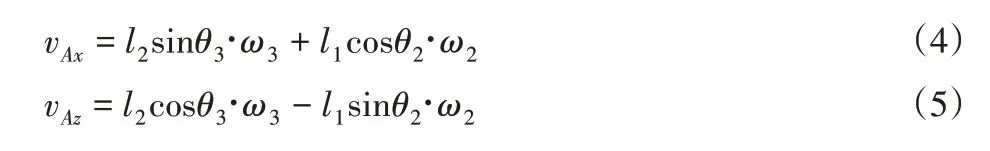
摆动侧膝关节相对运动水平速度与垂直速度：

则合成后膝关节B点加速度的水平分量aBx与垂直分量aBz可表示为：

根据刚体平面运动微分方程：

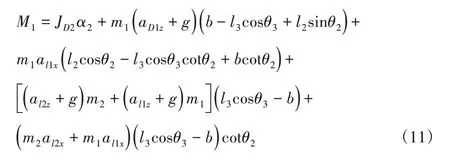
式中：al1与al2—上身l1与支撑侧大腿l2的质心加速度。

同理摆动侧膝关节驱动力矩M2亦可求出。

当人体在进行蹲起运动时，可能会受到不同的干扰外力，以及上身姿态可能会发生变化，因此膝关节力在这些影响因素下在相同时刻会存在不同值。在实际控制时需要实时计算出确定的膝关节力。因此，利用最小方差确定唯一驱动力矩。

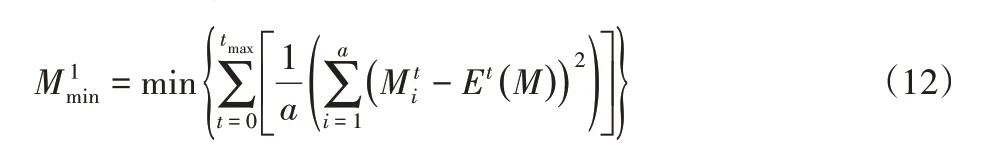
式中：a—t时刻膝关节力解的个数；Mit—t时刻第i个膝关节驱动力矩Et(M)为t时刻驱动力矩的算术平均值。

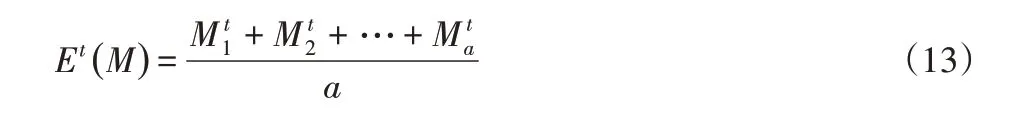
定义1M1与M2分别是蹲起时支撑侧膝关节与摆动侧膝关节的力矩，如果在蹲起的过程中M1与M2越接近于Mmin，则可认为M1与M2变化越平稳，蹲起过程就更稳定，因此这里提出上身负重载荷性能因子与来评价稳定性。

基于经济的全面建设，高速公路桥梁在高速公路建设中的重要性也逐渐突显出来。所以，高速公路桥梁施工质量也将直接影响高速公路稳定性，要强调桥梁基础的关键性。钻孔灌注桩施工技术的成本不高且操作方便，具有一定的适应性，所以被广泛应用在桥梁基础建设中。由此可见，深入研究并分析高速公路桥梁钻孔灌注桩的应用与施工工艺具有一定的现实意义。

3.2 干扰外力因子

在蹲起过程中，要确保人体在蹲起过程中保持稳定，就不能忽略外部环境的影响。我们要确保人体在蹲起过程中受到外力干扰时的稳定性就必须对失稳危险的范围进行量化。

当人体在蹲起过程中受到一些期望或非期望的外界干扰力Qi(i=1…m)时，其实际ZMP位置矢量投影：

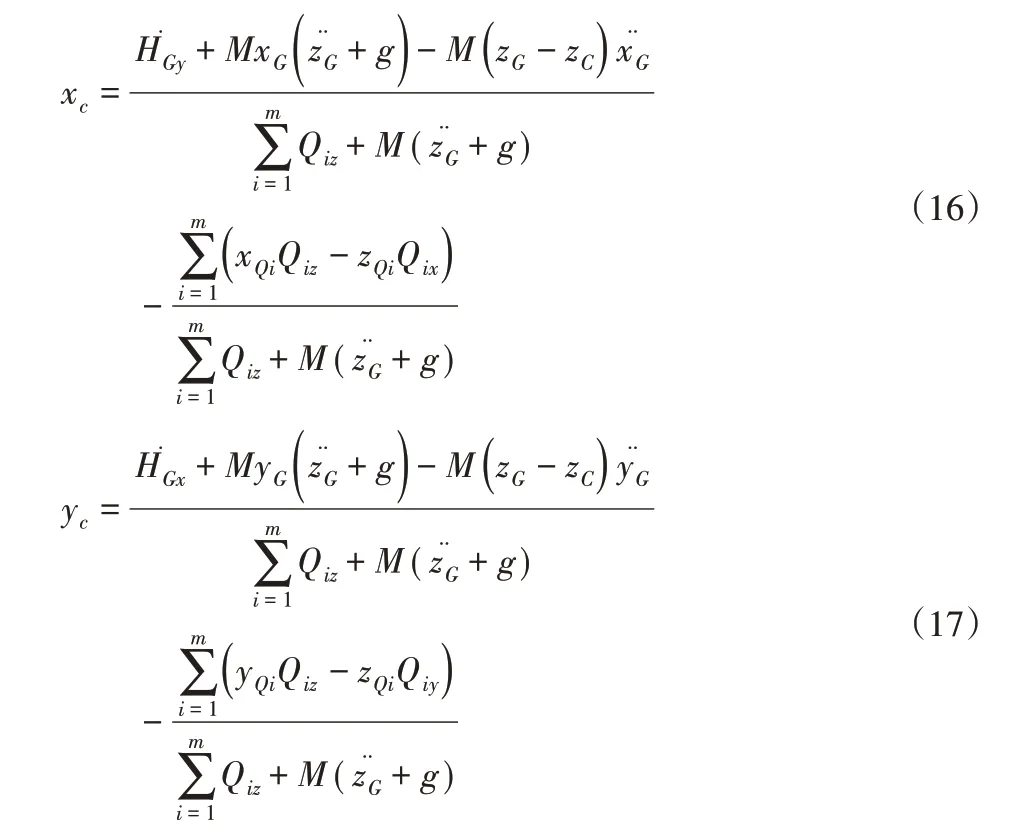
当人体不受外界干扰稳定的期望ZMP：

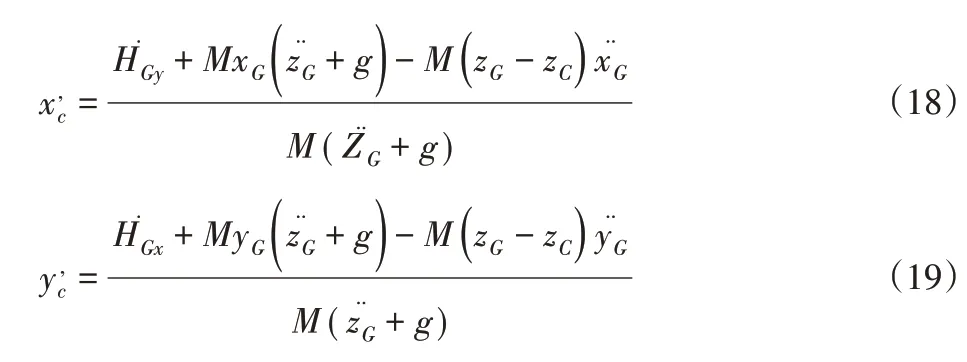
式中：HG—整个身体质心的瞬时转动力矩；M—总质量。

式中：HGi—第i个连杆的瞬时转动力矩。

定义2 人体在蹲起过程中受到外力干扰时，要确保其稳定性就要保证实际ZMP尽可能的接近期望ZMP。因此提出外力性能因子ξF1与ξF2来评价蹲起过程中实际ZMP与期望ZMP之间的距离。

当实际ZMP的横坐标与纵坐标与期望ZMP的横纵坐标接近时，ξF1、ξF2的值接近1，表示蹲起过程越稳定。

3.3 人体姿态性能因子

人体在起身过程中，若上半身只绕Z轴旋转并不会对其稳定性造成影响。若上半身发生X、Y轴方向的倾斜则会对稳定性产生影响，特别是身体左右倾斜时，倾斜角过大时甚至会出现跌倒状况。所以应避免此现象的发生。故设定姿态性能因子ξα1与ξα2。

定义3设定姿态性能因子ξα1与ξα2来衡量身体倾斜程度是否过大，表示如下：

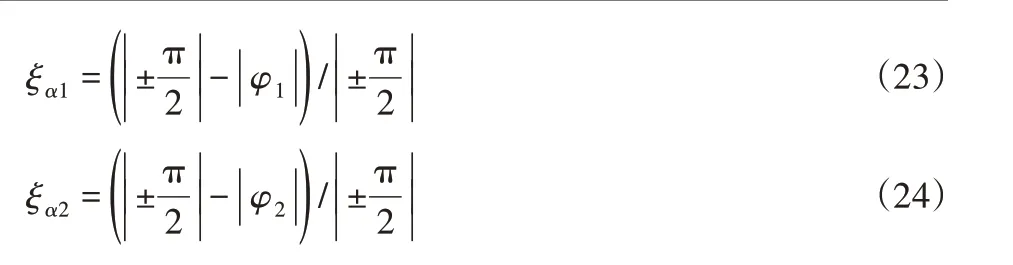
当ξ1与ξ2越小时，上半身的姿态角φ1、φ2越接近±，则其稳定性越低；反之，ξα1与ξα2越大时，上半身的姿态角φ1、φ2越接近00，蹲起过程稳定性越高。

4 蹲起运动过程稳定性评价

由于蹲起运动是通过膝关节驱动来实现的，因此在蹲起运动过程中受到外界干扰时，其运动状态可能会发生变化，稳定性会受到影响。故评该蹲起过程的稳定性是指，蹲起过程受到外界干扰时，身体在能够完成蹲起运动时抵御干扰的能力。对蹲起运动过程造成影响的三个因素：上身负重、在蹲起过程中受到的外力干扰以及上半身的晃动。

在整个蹲起运动过程中，当人体受到外界干扰力作用与上半身姿态一定时，负重不同时，该过程的稳定性也不同；当负重与上半身的姿态一定时，若身体受到预期之内或预期之外的干扰力作用时，整个运动过程的稳定性也会受到一定的影响；当负重与外力干扰一定，那么上半身若发生大幅度的晃动，显然也会对该运动过程的稳定性造成很大的影响。因此，在稳定性研究中综合考虑人体上身负重、身体受到的外力干扰以及上身姿态三个因素，通过加权的方式得到人体蹲起运动状态下的稳定性评价指标Ld，整个蹲起运动过程可以用稳定性评价指标Ld来评价整个过程的稳定性，而且加权之后Ld的数值大小可以评价蹲起运动过程的稳定裕度，直观的展现出蹲起过程中某个时刻的稳定程度。Ld表达式如下：

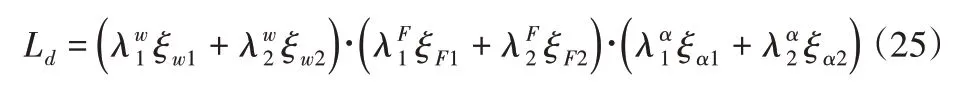
加权系数选取原则：一般情况下，各组加权系数选取与之相对应的优化目标相关，对于相同的优化目标，选取不同的加权参数与即使是相同的运动状态，其稳定裕度也会不同。在人体蹲起运动稳定裕度求解过程中，加权系数反应了蹲起过程中的上身负重载荷因子、干扰外力因子与上身姿态因子在整个运动过程中对其稳定性的重要程度。

不管哪种情况对该运动过程都是极为不利的，所以取ξw1=表示外力干扰因子ξF1与ξF2对整个运动过程稳定裕度的影响与贡献程度，由于蹲起过程中FZMP在X、Y平面上的矢量投影需要接近稳定状态下ZMP才能保证蹲起运动的稳定性，所以不管是X方向还是Y方向，对其稳定裕度的影响都是相同的，所以取表示上身姿态性能因子对蹲起过程稳定裕度的贡献程度，上半身身体的晃动会使身体的质心发生改变，同时由于是蹲起运动，上半身略微的前倾或后仰并不会对整个运动过程的稳定性产生较大的影响，但是若上半身在蹲起过程中发生左右倾斜就会对整个运动的稳定性造成巨大的影响，因此对整个运动过程的稳定裕度的贡献大且影响程度高。综上可取较为客观的评价上半身姿态性能因子对蹲起运动过程稳定程度的影响。

人体蹲起运动稳定性评价指标Ld的取值范围Ld∈(0，1 ]，Ld越接近0说明在蹲起过程中人体姿态极不稳定随时或即将发生跌倒其稳定裕度逼近于0；Ld=1表示当前运动状态极为稳定，没有受到外界丝毫干扰，是一种极为理想的运动状态，其稳定裕度为1；其他运动状态的稳定裕度在0与1之间。

5 实验与分析

5.1 人体模拟实验

本次实验由8个压力传感器、4个角速度传感器以及一个惯性传感器构成数据获取系统，传感器种类及布局，如表1 所示。选取十名身高175.0cm左右，体重65kg左右，身体健康的男性实验者分别进行双膝对称蹲起运动与单膝不对称蹲起运动，每名实验者分别在无任何干扰以及施加干扰的情况下做3组蹲起运动，每组10次，如表2所示。

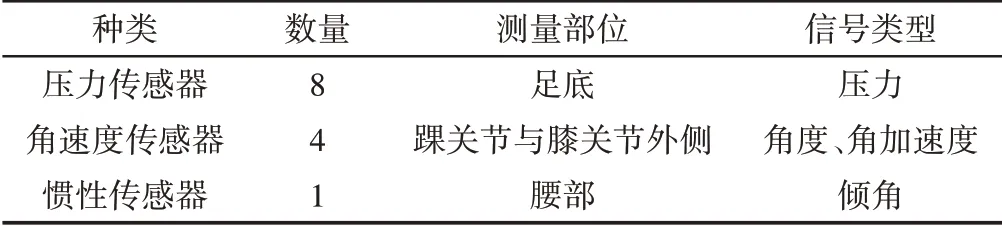
表1 传感器种类及布局Tab.1 Sensor Type and Layout

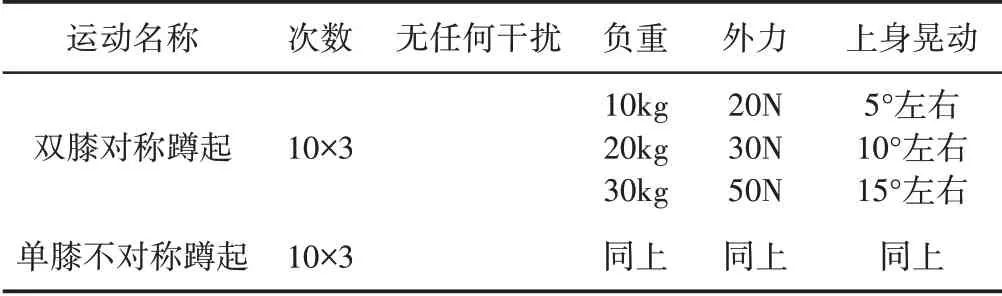
表2 实验详情Tab.2 Experimental Details

为减少噪声信号对蹲起运动数据采集的影响，利用中值滤波算法对原始数据进行预处理，这样既保留了各个传感器原始数据的数据特征，还很好的过滤掉了噪声对原始数据的影响[10]。将与处理过的数据导入到MATLAB 中，根据上文动力学方程编程计算求解，得到双膝蹲起过程与单膝蹲起过程稳定性变化情况。实验设备与实验流程，如图2所示。人体运动模式，如图3所示。

图2 实验设备与实验流程Fig.2 Experimental Equipment and Process

图3 人体运动模式Fig.3 Human Movement Mode

5.2 仿真验证

除了进行人体蹲起实验验证，还运用仿真软件对蹲起过程稳定性进行研究。首先利用Solidworks软件建立人体简化模型，再把模型导入到ADAMS 中。为保证仿真与人体实验结果对比的可靠性，因此在ADAMS仿真中模型的规格参数、运动状态、受到的外界干扰以及蹲起运动次数都要与人体实验相同。其中单膝蹲起运动，如图4所示。同样的将ADAMS仿真得到的数据导入到MATLAB中，利用之前编程好的程序进行求解，最后用plot得到结果图。

图4 单膝蹲起模拟图Fig.4 Simulations of Crouching on One Knee

5.3 结果分析

无干扰下双膝对称蹲起与单膝不对称蹲起对比图，如图5所示。从图5中可知，经过人体实际数据采集与软件模拟可以看出，当人体不受外界干扰时，单膝不对称蹲起运动与双膝对称蹲起运动稳定性大致相同，但是单膝蹲起运动稳定裕度的最低值要大于双膝蹲起运动的最低值，单膝蹲起运动要更加稳定。同时还发现不管是单膝蹲起运动还是双膝对称蹲起运动，其稳定性变化都呈现出先降低后增大的趋势。

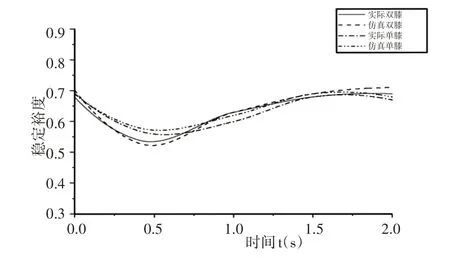
图5 无干扰下双膝对称蹲起与单膝不对称蹲起对比图Fig.5 Comparisons Between Symmetrical Squatting of Knees and Asymmetrical Squatting of One Knee without Interference

负重20kg下蹲起对比图，如图6所示。从图6可以了解到当人体受到20kg 的负重时，稳定性相对于图5 来说有了明显的变化，且可以明显的区分出单膝对称蹲起与双膝不对称蹲起时的稳定性大小差异当人体负重达到30kg 时，该变化程度更加明显。单膝蹲起运动稳定性在运动全程都大于双膝蹲起运动，说明人体的负重是影响蹲起运动的重要因素，且在有负重的情况下单膝蹲起运动的稳定性要高于双膝蹲起运动的稳定性。

图6 负重20kg下蹲起对比图Fig.6 Comparisons of Squatting and Lifting with 20kg Load

从图7可知，当人体受到20N的干扰外力时，稳定性在蹲起前期变化幅度很大，随着人体逐渐站立起来稳定性也随之增大。上身晃动角度在10°左右人体进行蹲起运动时的稳定性变化情况，如图8所示。从图8中可知，双膝蹲起运动稳定性的最低值要大于单膝蹲起运动稳定性的最低值，当受到的干扰外力接着增大时或者上身晃动的角度也接着变大时，该现象更加明显。这说明，单膝蹲起运动的稳定性要比双膝蹲起运动稳定性高，更不易出现跌倒的情况。

图7 20N干扰外力时蹲起对比图Fig.7 Contrast of Squatting When 20N Interferes with External Force

图8 上身晃动10°左右蹲起稳定性对比图Fig.8 Stability Comparison of Squatting with Upper Body Shaking Around 10 Degrees

身体负重20kg的情况下，稳定裕度分别保持在0.3、0.45、0.6时，干扰外力、上身晃动与时间的对应关系，如图9～图11 所示。从图中可以看出，在蹲起前期（0～0.4）s时，干扰外力与上身的晃动角度范围很大，但是在（0.4～1.0）s时稳定裕度要想继续保持在0.45时就要减少干扰外力或上身的晃动角度，在1.4s以后由于人体基本达到站立姿态，因此身体可以承受较高的外界干扰。

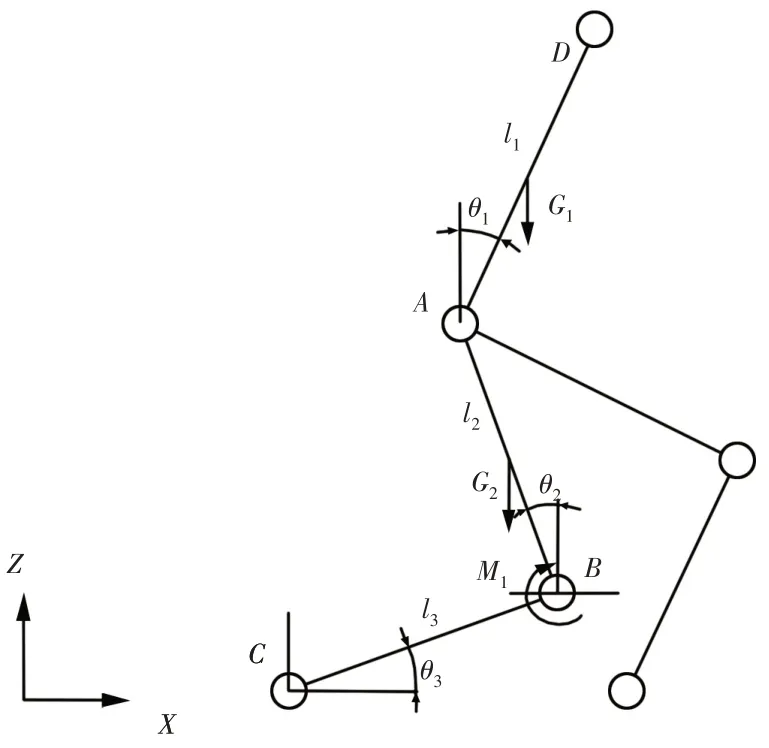
图1 人体简化刚体模型Fig.1 Simplified Rigid Model of Human Body

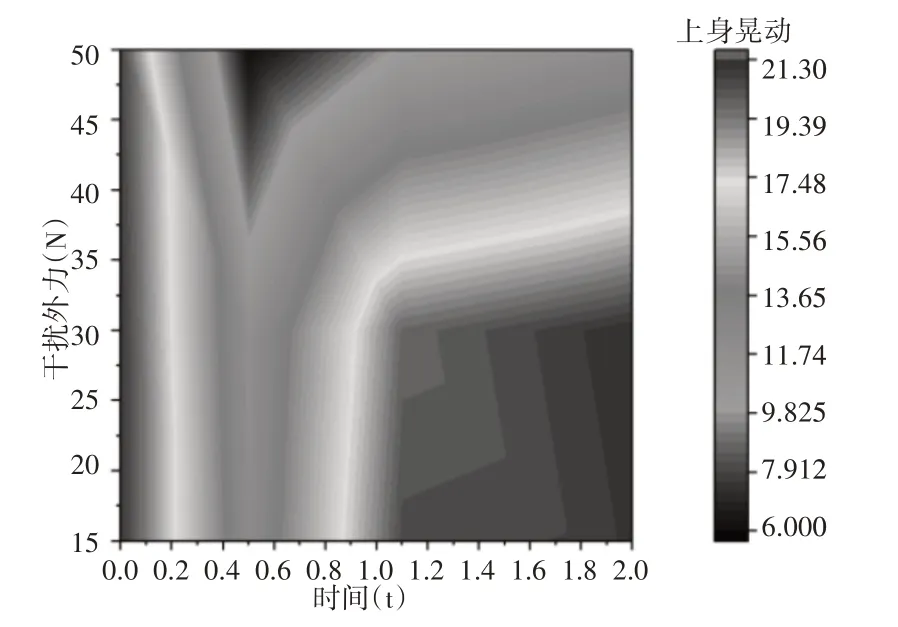
图9 身体负重20kg的情况下，稳定裕度保持在0.3时，干扰外力、上身晃动与时间的对应关系Fig.9 Weight-Bearing 20kg，Stability Margin0.3，Corresponding Relations Between Disturbing External Force，Upper Body Posture and Time

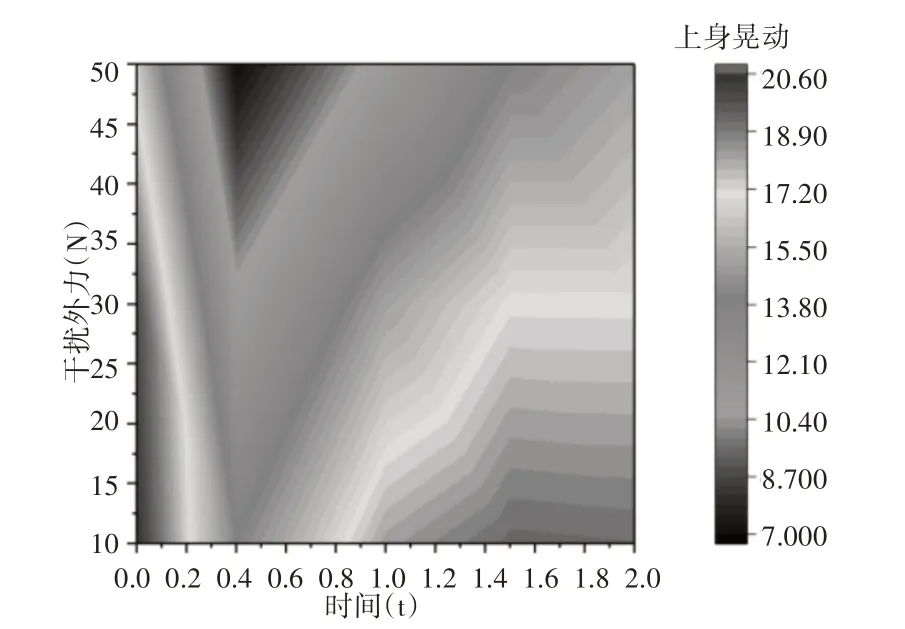
图10 身体负重20kg的情况下，稳定裕度保持在0.45时，干扰外力、上身晃动与时间的对应关系Fig.10 Weight-Bearing 20kg，Stability Margin0.45，Corresponding Relations Between Disturbing External Force，Upper Body Posture and Time

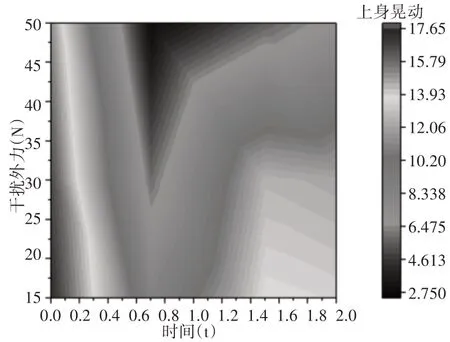
图11 身体负重20kg的情况下，稳定裕度保持在0.6时，干扰外力、上身晃动与时间的对应关系Fig.11 Weight-Bearing 20kg，Stability Margin0.6，Corresponding Relations Between Disturbing External Force，Upper Body Posture and Time

综上所述，人体在蹲起运动过程中前期的稳定性较差并且身体负重、外力的干扰以及人体晃动这三种因素相互关联都对的蹲起运动有着较大的影响，在分析人体运动时特别是不对称运动时要着重研究这三种因素。

6 结论

（1）人体在进行对称运动与不对称运动时，人体的稳定性由多个因素相互影响的，有外界的干扰因素与自身的干扰因素，不能简单地只考虑一种影响因素。

（2）在人体运动中，特别是蹲起运动中，影响蹲起运动的稳定性因素主要有自身的负重、干扰外力以及上身晃动，这三种因素对人蹲起运动的稳定性影响程度最大。在以后更深层次地研究蹲起运动稳定性时，要着重考虑这三种因素的影响。

（3）通过人体运动实验与ADAMS软件仿真，验证了推导公式及理论的正确性。利用此理论可以得到人体在稳定运动情况下的自身运动与外界干扰的边界值，为今后深入研究人体运动稳定性打下了一定的理论基础，不止于此，该理论同样可以应用到的拟人机器人或下肢外骨骼的稳定性研究中。