逆响应面法用于磨机传动系统的模型修正

陶 征，张 鹏，郭勤涛

（1.郑州大学机械与动力工程学院，河南 郑州 450001；2.南京航空航天大学机电学院，江苏 南京 210016）

1 引言

磨机是选矿工艺中一个十分重要的设备。然而，恶劣的工作环境及高作业率，极大地增加了磨机，尤其是磨机传动系统故障的概率。而这样的关键设备一旦发生故障，往往给企业带来巨大的经济损失。基于试验检测结构的动态特性的变化，从而达到预测结构健康状况是当前解决这一问题的主要方法。然而，测点多、测点不全面以及无法实现实时在线检测是这一方法的主要问题。随着计算机技术以及有限元理论的发展，基于准确的有限元模型实现对结构的动态特性仿真代替现场试验进而实现对结构健康监测的方法，越来越受到业内人士的关注[1]。然而，准确的结构模型和模型的分析精度，是结构动力学仿真分析的关键，通过试验数据进行有限元模型的确认及其修正，尤其重要。

基于响应面的有限元模型修正方法是近年来有限元模型修正技术研究的热点[2-6]。其以显式的响应面模型接近拟合特征参数与设计参数间较为复杂的隐式函数关系，可以很好地解决机械结构中存在的不确定参数这一问题[7]。然而，基于响应面法的有限元模型修正在求解不同特征量对应的设计参数修正量时，则必须通过迭代寻优算法来求解，在实际工程应用中仍不太方便。针对这一问题，文献[8]在逆系统应用方法的基础上提出了逆响应面方法。该方法可以直接得到设计参数与特征参数之间的显式表达式。在获得逆响应面模型后，无需迭代寻优计算，即可直接计算出不同特征量对应的设计参数值。目前，该方法的有效性已在桥梁设计中获得检验[8-10]，而机械工程领域中的应用实例尚未在相关文献中提及。

为了探讨和分析这一方法在机械结构动力学特性分析中的有效性，以磨机传动系统为对象，以其试验模态频率数据为目标值，基于逆响应面法实现磨机传动系统的有限元模型修正，验证了逆响应面法在机械结构动力学特性分析中的有效性。

2 逆响应面法修正的理论基础

2.1 基本思想

逆响应面法的基本思想是把输出变量作为自变量，输入变量作为因变量，通过更改响应面函数中输入变量与输出变量的关系，最后通过回归分析拟合出因变量和自变量之间的显式表达式。

利用逆响应面法进行有限元模型修正可以直接得到待修正参数（如密度、弹性模量等）与特征参数（如固有频率等）之间的显式表达式，在逆响应面的系数确定以后，不需要再进行迭代修正，即可根据特征参数的目标值直接得到待修正参数的修正值[8]。

2.2 试验设计

试验设计常用的方法有中心复合设计（central composite design，简称CCD）、均匀设计、D-最优化设计等[9]。中心复合设计常用于逆响应面试验设计，可以回归拟合一阶、二阶模型或更高阶模型，逆响应面模型通常为二阶模型，所以这里采用中心复合设计（CCD），对于2k析因设计，总设计点N由三部分组成：（1）中心点，即试验原点，共n（c试验中nc一般取1）个试验点；（2）坐标轴点，共2k个坐标轴点；（3）析因设计点，共2k个试验点，总试验点数N=1+2k+2k，对于逆响应面函数的回归系数个数M一般由式（1）计算[9]，其中，m—输入参数的个数。

2.3 逆响应面的拟合

在有限元模型修正中，通常采用二次多项式函数作为逆响应面函数，其表达的曲面即为逆响应面模型，函数形式即：

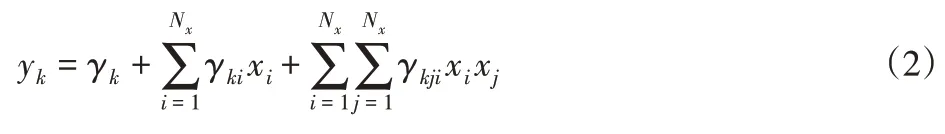
式中γk、γki、γkji—逆响应面函数回归系数；x（ii=1，2，……，Nx）—输入变量（特征参数）；y（ii=1，2，……，Ny）—输出变量（设计参数）；Nx—输入变量的数量；Ny—输出变量的数量［9］。得到样本数据以后，可以利用最小二乘法拟合得到式（2）的回归系数，即得到系统的逆响应面方程。

2.4 逆响应面精度检验

为得到逆响应面拟合的精度，利用平均相对误差来检验拟合结果的准确性，式（3）可以检验求解的误差大小。

式中：Nx—输入变量的数量—输入变量的目标值；—由有限元修正得到的特征参数的实际值[9]。在文中的实际工程应用中，通过模态试验获取特征参数的目标值，故可通过计算修正值的误差来分析逆响应面拟合的效果。如果误差太大，则可以通过增加逆响应面的阶次或者增加试验点来减小误差。

3 算例分析

某齿轮轴结构，如图1所示。轴总长507.7mm，材料属性：齿轮轴和盘的泊松比μ=0.3，弹性模量为210 GPa，密度为7850 kg/m3，前四阶试验模态数值分别为：421.23Hz、521.95Hz、1101.53Hz 和1891.57Hz。经有限元分析可知，泊松比对模态振型影响较小，其不作为设计参数。现以齿轮轴和盘的弹性模量与密度为待修正参数，以前四阶模态频率为特征参数进行模型修正，并与响应面法的修正结果进行对比分析。

图1 齿轮轴Fig.1 Gear Shaft

本次试验设计的特征参数是4个，设计参数是4个，试验点数N=25，回归系数M=15，N＞M，无需增加试验点数即可求解出逆响应面函数。利用CCD建立试验点并进行有限元分析得到的试验数据，如表1所示。其中，E1、E2表示齿轮轴弹性模量和圆盘弹性模量，ρ1、ρ2表示齿轮轴密度和圆盘密度，f1、f2、f3、f4分别表示前四阶模态频率。由表1中的试验数据经最小二乘法拟合得到的逆响应面函数如式（4）～式（7）所示。

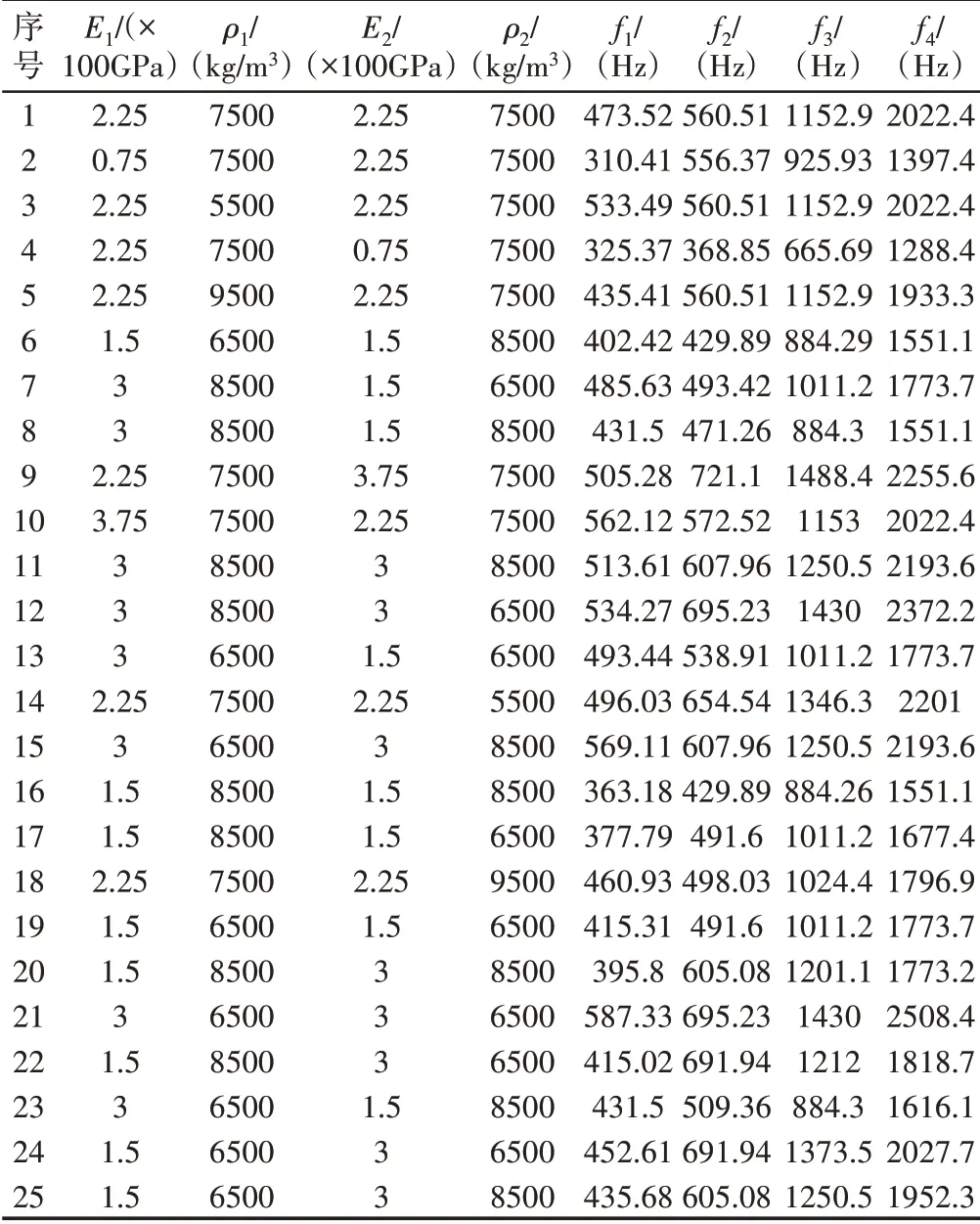
表1 试验数据Tab.1 Experimental Data

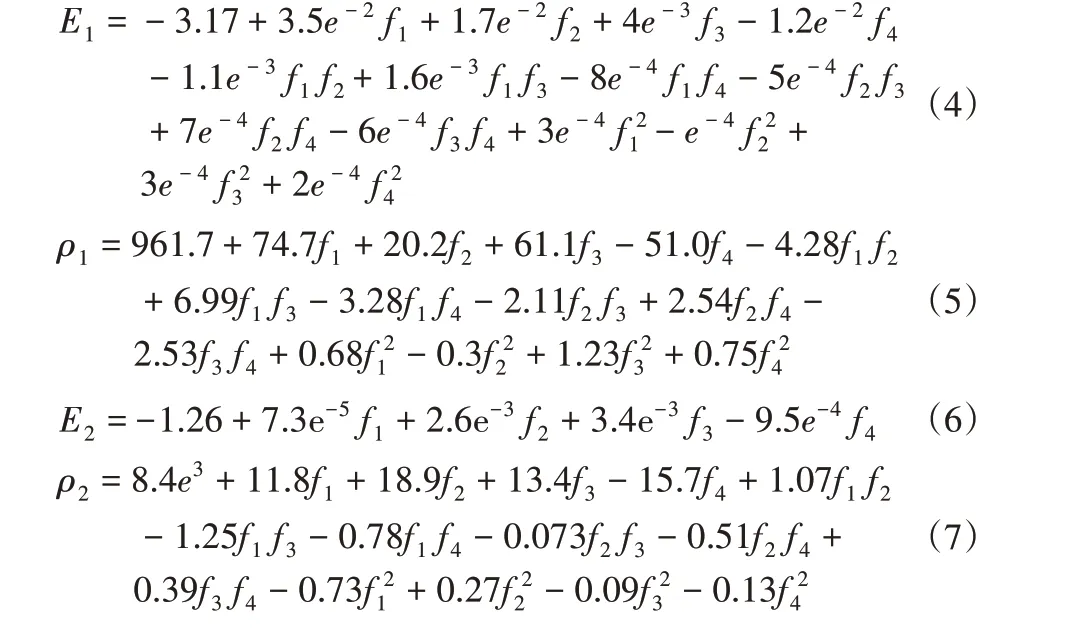
将实际的模态数值带入公式得到设计参数值，分别为163GPa，7250.8kg/m3，175GPa，6500.4kg/m3。将设计参数值带入有限元模型中分析得到修正后的模态频率，并与响应面法（采用相同的试验数据）修正结果对比结果，如表2所示。

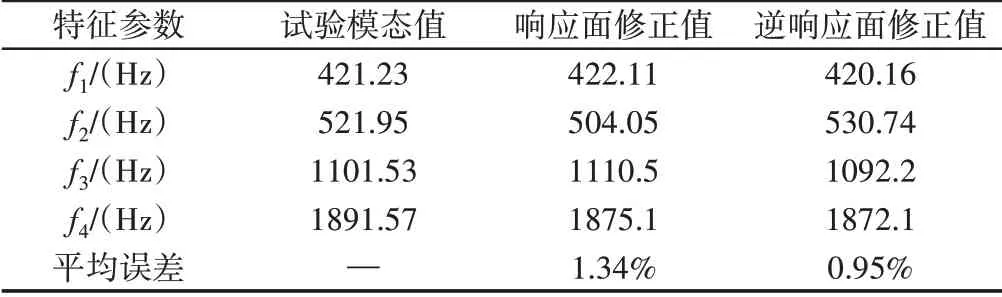
表2 结果对比Tab.2 Results Comparison

分析结果表明，在输入参数和输出参数数量相等的情况下，逆响应面法模型修正较响应面法模型修正效果更好，逆响应面法可以应用到机械结构的模型修正中。

4 工程实例

某7.9m 大型磨机传动系统，如图2 所示。图中：1—电机；2—联轴器；3—高速小齿轮；4—高速大齿轮；5—联轴器；6—小齿轮；7—磨机（包含筒体、齿轮和负载）。

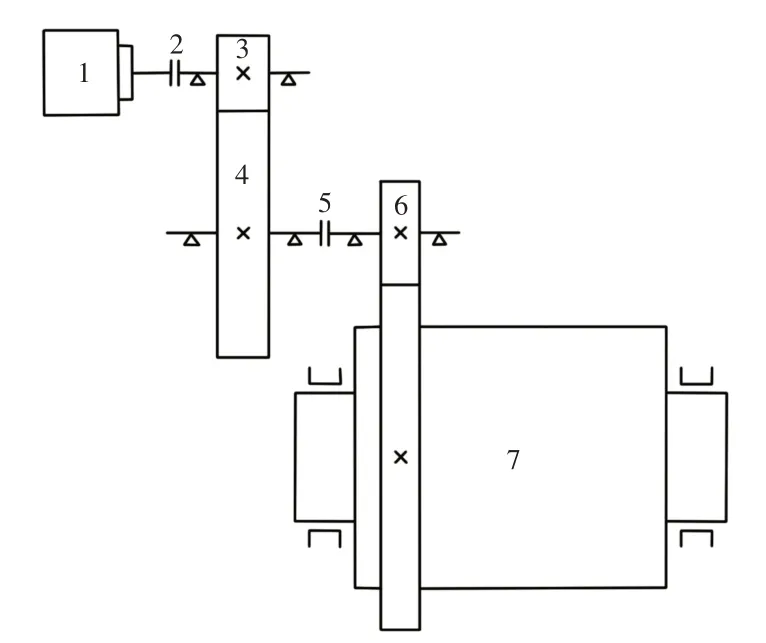
图2 某7.9m磨机传动系统简图Fig.2 Sketch of a 7.9m Mill Transmission System

大型磨机传动系统规格较大，在获取传动系统模态数据过程中不太方便，因此，以大型磨机传动系统为原生系统，基于齿轮传动系统的相似设计理论对原生系统组成元素识别，采用相同功能和作用的组成元素，设计并搭建了一级齿轮传动系统装置，如图3所示。依据各零部件在结构上的连接关系将传动系统拆分为输入轴子结构和输出轴子结构，子结构中包含传动轴及轴上零部件。这里以输入轴子结构为研究对象，基于逆响应面法对其进行模型修正。

图3 传动系统试验台Fig.3 Transmission System Test-Bed

模态试验坐标系和试验测点设计，如图4所示。图中的点为试验测点位置，测点共25个。由于测点数量较多，为得到整体振型，采用移动传感器的测量方式解决传感器数量较少的不足，分别测量各个测点的X、Y和Z三个方向的加速度信号，获得各个测点的数据信息。

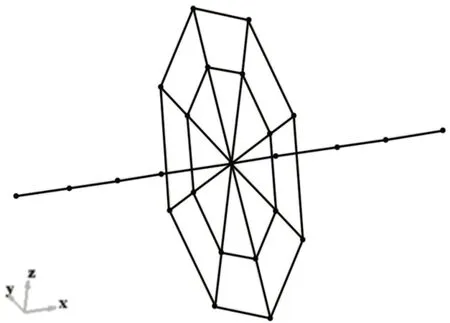
图4 模态实验建模Fig.4 Modal Experimental Modeling

利用N-modal模态识别软件对采集数据进行分析处理，识别各阶模态，模态试验结果，如表3所示。

表3 模态试验结果Tab.3 Modal Test Results

输入轴子结构的有限元模型，如图5所示。传动轴和齿轮之间以及传动轴和圆盘之间用bonded接触连接；轴承采用弹簧单元模拟。在模型建立过程中对子结构部分连接结构进行简化，导致模型中存在一定的误差，对未安装轴承状态下的输入轴子结构进行模型修正，识别传动轴、齿轮以及圆盘的材料参数，经过模型修正结果分析，小齿轮的材料参数不是显著参数，故将小齿轮和输入轴当作一种材料进行分析，识别材料参数，如表4所示。

图5 有限元模型Fig.5 Finite Element Model

表4 材料参数Tab.4 Material Parameters

这里的设计参数为轴承1 和轴承2 等效弹簧单元的刚度。轴承1和轴承2的初始刚度值分别为4.5e7N/m 和6.0e7N/m。以轴承等效弹簧单元的刚度为试验因素，以有限元模型模态分析结果的前两阶模态为响应值，采用CCD方法建立试验点设计试验，并在有限元模型中分析计算得到样本数据，如表5所示。基于表5的样本数据拟合逆响应面函数，如式（8）、式（9）所示。

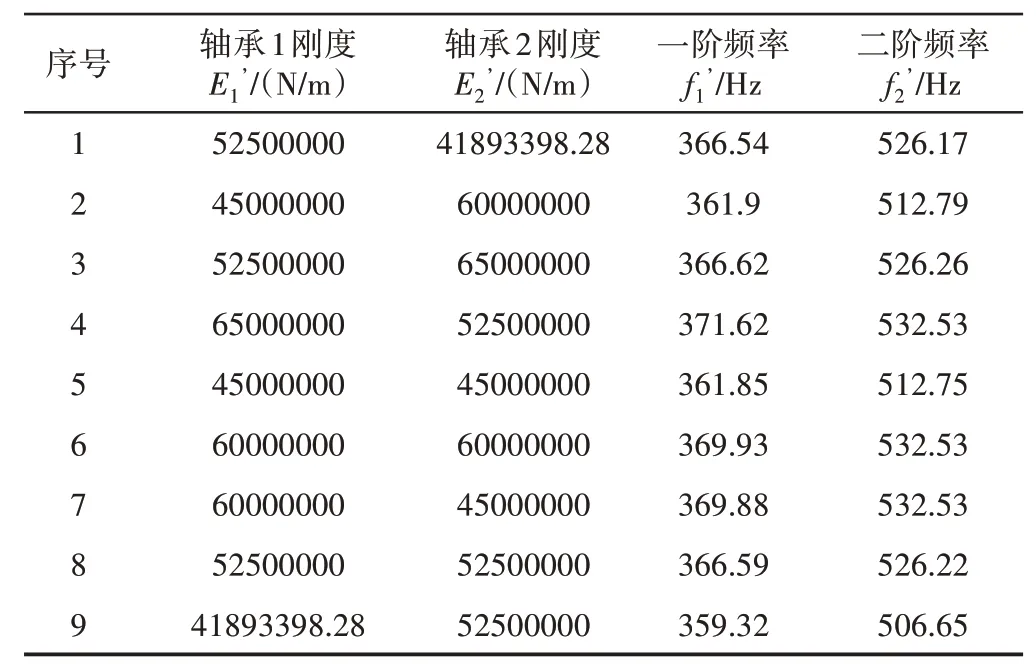
表5 试验数据Tab.5 Experimental Data

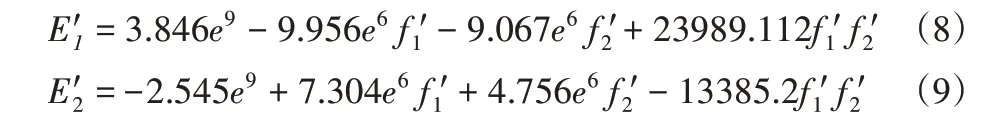
将表3的试验模态频率值带入逆响应面函数中即可得到修正后的刚度值，修正结果为：轴承1 刚度6.5e7N/m，轴承2 刚度5.27e7N/m。将刚度值带入有限元模型进行分析得到修正后的模态频率，并计算修正前后的模态频率误差，如表6所示。结果显示：有限元模型精度得到明显改善。因此，逆响应面法能有效地应用到机械结构动力学特性分析中。

表6 模态频率误差Tab.6 Modal Frequency Error

5 结论

通过采用逆响应面法对磨机传动系统进行模型修正修正，并分析验证该方法在机械结构动力学分析中的有效性。算例显示逆响应面法可用于机械结构的有限元模型修正中，且修正效果较优于响应面法，工程实例显示出逆响应面法在机械结构动力学特性分析中的有效性。

逆响应面法可直接得到设计参数关于特征参数的显式表达式，根据特征参数的目标值直接得到设计参数值，相比响应面法减少了迭代优化的过程，这不仅节省了很大的计算工作量，也为机械结构动力学特性分析提供了一种有效的方法，更为后续传动系统可靠性分析提供了准确模型。