样本熵和Vmd结合的轴承早期故障预测方法

雷春丽，曹鹏瑶，崔 攀，张晨曦

（1.兰州理工大学机电工程学院，甘肃 兰州 730050；2.兰州理工大学数字制造技术与应用省部共建教育部重点实验室，甘肃 兰州 730050）

1 引言

滚动轴承是主轴系统中的重要零部件，但也是最容易损坏的部件，当轴承出现局部损伤时，相互接触的元件，在带载运转的过程中相互碰撞产生周期冲击特征，而这种碰撞会导致旋转轴出现抖动，影响设备的正常运行[1]。当轴承出现早期故障时，如果能及时发现并进行诊断维修，就可减少因轴承故障所造成损失。所以，对滚动轴承早期故障预测方法的研究具有重要意义。

针对轴承的故障特征提取与故障预测问题，国内外学者做了很多的研究。文献[2]提出一种基于振动谱分析的轴承状态监测方法，利用该方法对轴承在使用寿命期内的振动特性进行了研究；文献[3]提出基于灰色支持向量机模型的滚动轴承故障诊断与预测方法；文献[4]将GS-ASTFA 算法应用于滚动轴承趋势分析中；文献[5]提出一种基于VMD的方法，利用该方法对轴承不同位置的故障特征进行了分析；文献[6]提出一种基于SVD和熵优化频带熵的滚动轴承故障诊断的研究方法；文献[7]提出基于VMD的滚动轴承早期故障诊断方法；文献[8]提出一种基于参数优化VMD和样本熵的滚动轴承故障诊断方法。综上所述，研究人员提出了不同的算法进行轴承故障诊断与预测，但关于轴承潜在的、早期的故障预测还缺乏有效的识别和预示手段。此外，很多故障预测的算法都需计算出故障的频率特征，需要知道轴承的运行参数以及结构，以上方法虽然有效，但过程较为复杂。

提出了将样本熵和变分模态分解结合的轴承早期微弱故障预测模型，该模型以样本熵特征作为描述轴承性能的健康指标，根据健康指标的非平稳特征，进行变分模态分解，挖掘了数据样本的深层次隐含信息，提取了时间序列的趋势项，预测出轴承早期微弱故障信息，并结合具体实验，验证了该方法的有效性。

2 样本熵

2.1 算法描述

样本熵是文献[9]于2000 年提出的熵算法。假设存在数据为N个，组成的时间序列X=[x(n)，n=1，2，…N]，样本熵表达式为：

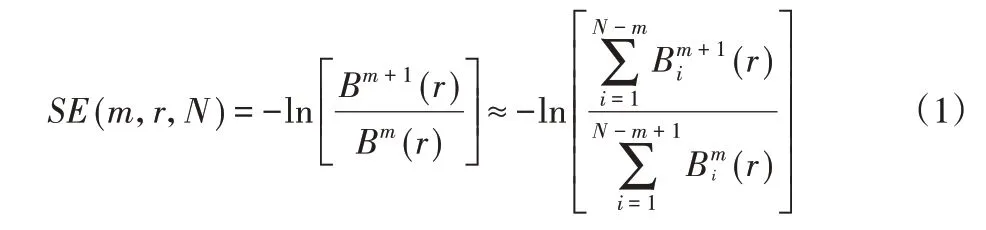
式中：m—嵌入维数；r—相似容限；Bm(r)—两个序列在相似容限下匹配m个点的概率；Bm+1(r)—两个序列匹配m+1 个点的概率。

2.2 参数选择

从前文算法描述中可知，选择合适的嵌入维数m、相似容限r、数据点数N，对于计算结果甚为重要，参数选取指标如下[10]。

（1）嵌入维数m：一般情况下，m=1或2。

（2）相似容限r：r多数选取(0.1～0.2)δx，其中δx指得是数据标准差。

（3）数据点数：一般取值为（100～5000）点。

取m=2，r=0.2δx，N=4096。

样本熵是描述时间序列复杂度的指标，在利用样本熵算法进行试验数据处理时，因数据量较大且对样本熵值精度要求不高，为计算方便舍弃了一些数据。而样本熵对数据丢失不敏感，即使丢失了一部分数据，对其整体数值大小以及变化趋势影响不大。

3 变分模态分解

VMD 方法在分解信号时，通过迭代搜寻变分模型最优解来确定各分量的频率中心及带宽，进而自适应地实现信号的频域剖分及各分量的有效分离，VMD算法分解精度更高且有良好的抗模态混叠和噪声鲁棒性[11]。VMD分解时，把高频、中高频、中低频、低频部分分解开。因此，选取VMD分解方法。

VMD 算法需要确定的主要参数如下[8]：凸函数优化相关系数tau、中心频率初始化设置init、中心频率更新时的相关参数DC、判别精度、惩罚因子和分解层数K，其中前四个参数对分解效果影响较小，设置为经验值，即tau=0，init=0，DC=1，判别精度ε=1e-6。而惩罚因子和分解层数K对VMD分解结果影响较大这两个参数的选择将在第五章中详细阐述。4样本熵-VMD轴承早期故障预测模型。

样本熵值可以反映时间序列复杂度，且轴承样本熵值可反映轴承不同的运行状态，因此，可以把轴承的样本熵值作为轴承健康状态时间序列。但在分析振动信号中，样本熵值的大小并不总是和时间序列的复杂度有关。根据数据的样本熵值，得出轴承健康状态时间序列，并不能够完全预测轴承早期故障。

为更精确地进行轴承早期故障预测，需找到能反应轴承运行状态的趋势项，趋势项是指振动信号中的周期比记录长度大的部分。而VMD可以将不同的频段分解，故VMD分解的低频部分可以反映轴承运行状态的趋势。因此，采用样本熵-VMD模型进行轴承早期故障预测，该模型综合利用了两种单项算法的优点。

轴承早期故障预测建模过程如下：

（1）对轴承振动信号进行处理，求解振动信号的样本熵值，构建轴承健康状态时间序列。

（2）采用VMD 算法对轴承健康状态时间序列进行分解，得到健康状态时间序列的各模态分量IMF。

（3）根据经典的相关系数、峭度、方差原则，选取最能代表原始数据的趋势项，将其趋势项单独作图。

轴承早期故障预测模型流程，如图1所示。

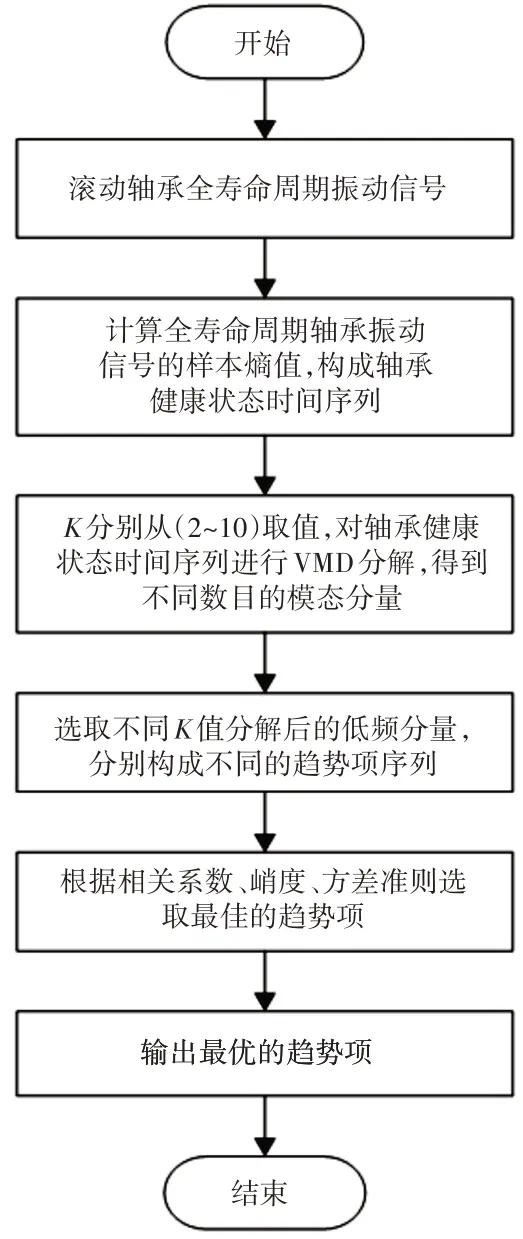
图1 样本熵-VMD模型轴承早期故障预测流程图Fig.1 Early Failure Prediction of Bearing Based on Sample Entropy-Vmd Model the Flow Chart

4 实验分析

为了更好地验证样本熵-VMD方法对故障预测的有效性，实验数据采用国外某大学用智能维护系统采集的全寿命周期滚动轴承数据[12]。滚动轴承型号为ZA2115，参数，如表1所示。电机转速为2000r/min，采样频率为20kHz。试验台，如图2所示。

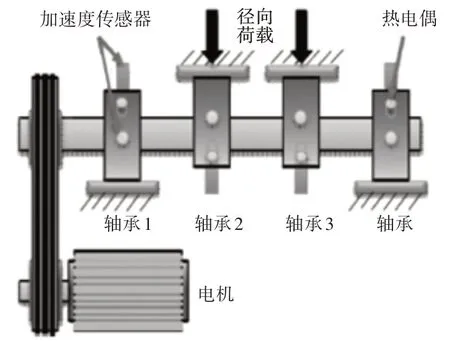
图2 轴承与传感器安装位置Fig.2 Mounting Position of Bearing and Sensor

表1 滚动轴承结构参数Tab.1 Structural Parameters of Rolling Bearing

该组实验采集的每个样本20480 个点，共采集984 个样本，试验持续时间为164h。实验轴承的振动数据，如图3所示。

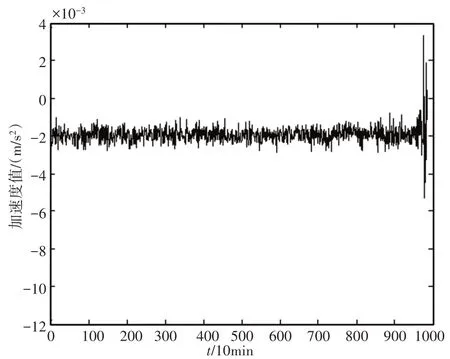
图3 全寿命周期轴承加速度图Fig.3 Full Life Cycle Bearing Acceleration Diagram

对原始振动数据进行处理，得到其样本熵数据图，构成轴承健康状态时间序列，如图4所示。

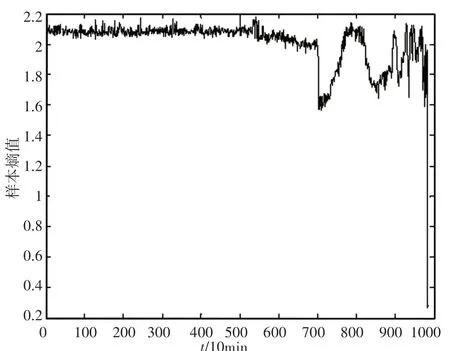
图4 轴承健康状态时间序列Fig.4 Time Series of Bearing Health Status

由图4可看出，随着轴承的不断运行，轴承健康状态时间序列呈下降趋势。从熵的机理分析，轴承正常状态下时间序列的复杂度要低于故障状态下的复杂度，曲线应呈上升趋势；然而在滚动轴承故障研究方面，样本熵并不总是与时间序列复杂度有关，样本熵值也受序列周期性的影响，样本熵对周期序列表现出较低的熵值。轴承运行过程中，会产生故障，而随着故障的发展，周期冲击特征会越来越明显，即样本熵值会呈现下降趋势。

进行VMD分解时，惩罚因子α和分解层数K对VMD分解结果影响较大。文献[13]指出VMD在分析振动信号时，惩罚因子α取较小值；在分析趋势项信号时，惩罚因子α取较大值。α通常取值100，1000，10000。为了更清楚的表示不同α值对低频分量的影响，以K值等于2为例，对轴承健康状态时间序列进行VMD分解，分别作出α为100、1000、10000时的低频分量图，如图5所示。从图5可看出，α值越大，曲线变得更为平滑。因此，当惩罚因子α取较大的值时，适用于提取较低的频率成分。用于轴承故障趋势预测，α取较大值，即取α=10000。

图5 不同α值下的低频分量Fig.5 Low-Frequency Components at Different α Values

主要讨论分解层数K对趋势项的影响，通过尝试不同的K值，根据相关性、峭度、方差准则，找出最优的趋势项时K的取值。对轴承健康状态时间序列进行VMD分解，由于VMD分解时K值不同，得到的模态分量IMF数目不同，其低频分量也不同，其反应的轴承运行状态的趋势也有所差异。因此，将K分别从（2～10）取值，得到不同数目的模态分量，分别计算不同K值下低频分量与轴承健康状态时间序列的相关系数以及轴承健康状态时间序列的峭度，如表2所示。

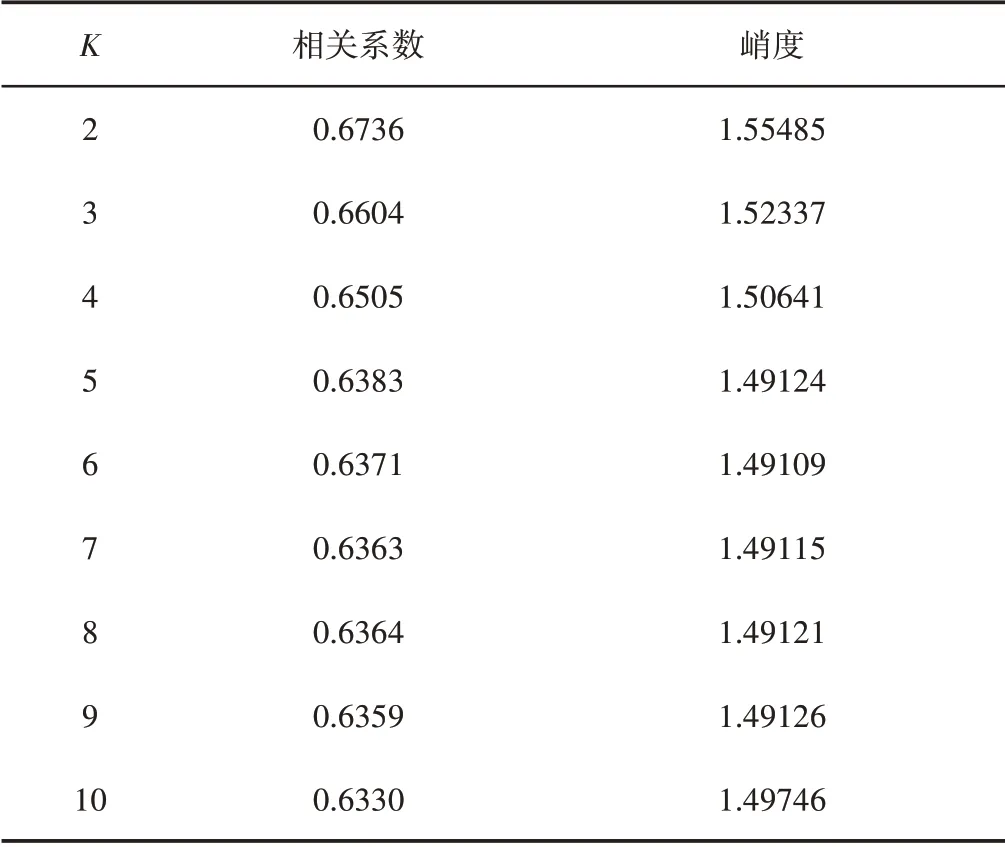
表2 低频分量与轴承健康状态时间序列的相关系数及峭度值Tab.2 Time Series of Low-Frequency Components and Bearing Health Status Correlation Coefficient and Kurtosis

由表2可看出，相关系数随K值增大而呈现变小的趋势。随K值增大，峭度在K值为（2～6）时呈下降趋势，在K值为（6～10）时呈上升趋势，为了找到峭度最大时K的取值，需要计算K=11时的峭度。经计算，K=11时，其峭度为1.49157，小于K值为10和2时的峭度值。由表2可得K=2时相关系数及峭度值都是最大的，最能反映其原始数据的趋势。分别将不同K值下的低频分量与轴承健康状态时间序列拟合，由于篇幅限制，仅列举K=2、3、4时的拟合图，如图6所示。

图6 不同K值的拟合Fig.6 Fitting of Different K Values

从图6中可看出，随着K值的增大，两条曲线的拟合程度越来越差，但图中表示不明显，因此，进一步计算低频分量与轴承健康状态时间序列差值曲线的平均值和标准方差，如表3所示。

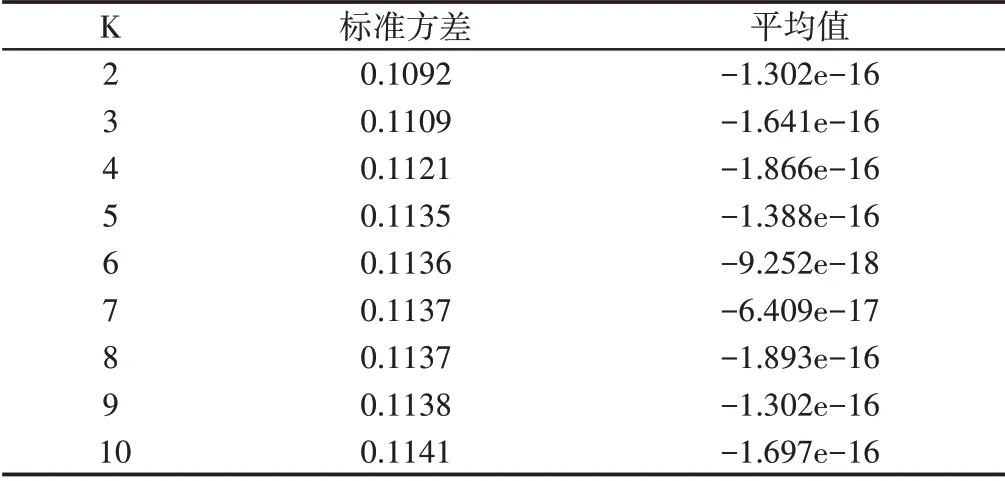
表3 不同K值下低频分量与健康状态时间序列差值的参数Tab.3 Parameters of the Difference Between Low-Frequency Components and Health Time Series Under Different K Values

由表3可看出，随着K值的增大，差值曲线的标准差随之增大，说明差值曲线越来越不稳定。综上所述，选取K=2时VMD分解得到趋势项是最佳的趋势项。采用样本熵和VMD模型对轴承故障预测结果，如图7所示。从其趋势项可以看出在5000min时轴承就已经出现明显的故障。

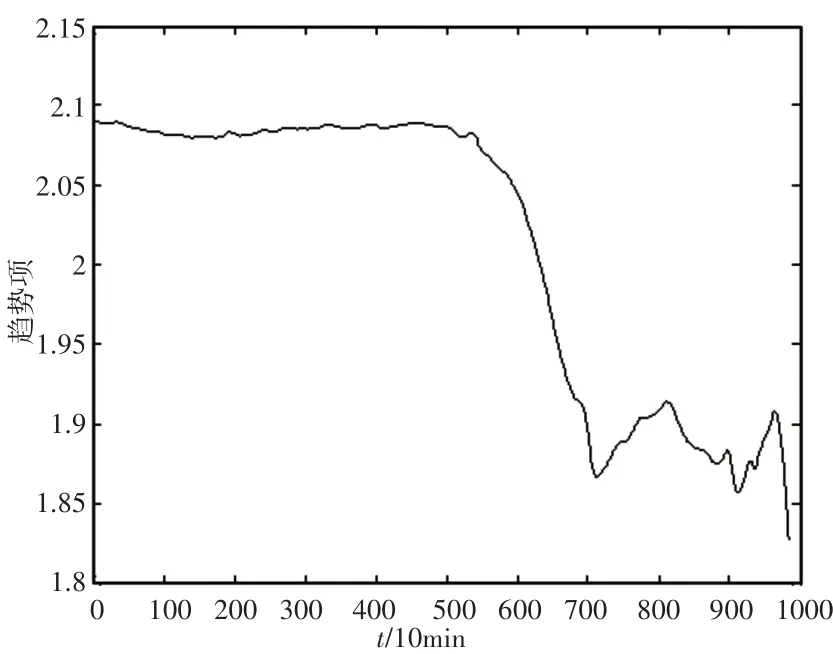
图7 轴承运行状态的预测趋势Fig.7 Prediction Trend of Bearing Running State

为了说明本预测模型的有效性，现采用绝对平均值和峭度两个指标分别预测轴承故障，这两个指标的变化可以反映滚动轴承全寿命周期运行状态，该轴承振动信号的绝对平均值和峭度的变化，如图8、图9所示。在7000min左右时，观测出绝对平均值和峭度值均有所变化，说明此时轴承已经出现早期故障。

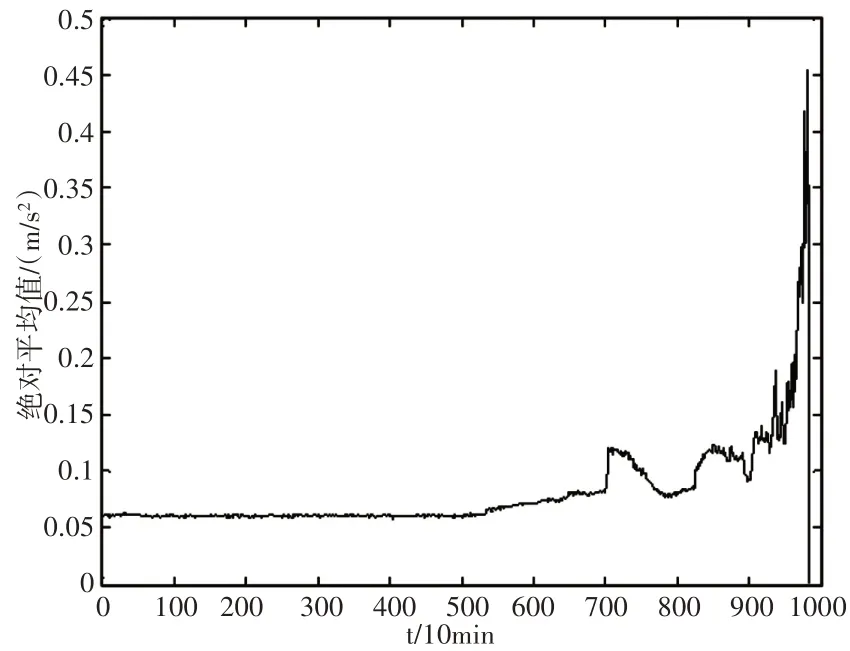
图8 绝对平均值Fig.8 Absolute Mean

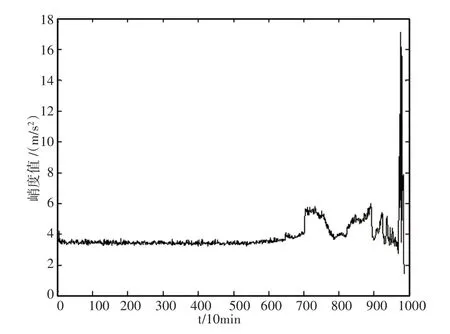
图9 峭度Fig.9 Kurtosis

通过图7～图9的计算结果可以看出，提出算法与其他时域指标相比，故障预测提前了2000min左右。证明了样本熵-VMD算法可以更好地预测轴承早期微弱故障。

5 结束语

（1）结合样本熵和VMD分解的特点，提出将样本熵-VMD算法应用于滚动轴承早期故障的预测，对全寿命轴承振动数据进行分析。研究结果表明，该方法计算过程简单，且比传统的轴承故障预测指标能更早地预测轴承的运行状态，可以避免重大故障的发生。（2）VMD分解时有两个对分解结果影响较大的参数：α和K。通过对比分析，得出结论：在分析趋势项时选用较大的α值。利用相关系数、峭度、方差准则，使得趋势项与原数据的相关性、趋势项的准确性以及稳定性都更高，根据这三者的规律性，选用K值为2进行VMD分解。（3）基于VMD算法早期故障预测的方法研究较少，许多方面亟待完善，比如K和α等参数在不同分析要求下的确定方法需要更加完善的理论支撑。