基于量纲分析法的爆破振动速度预测模型研究*

李修贤，程贵海，谭成驰，梁陆佳

(广西大学 资源环境与材料学院，广西 南宁 530004)

0 引言

爆破技术是一把双刃剑，将其应用于工程建设取得经济效益的同时，也不得不面对其带来的负面影响，其中爆破振动效应是产生危害的主要因素。随着爆破技术的不断发展，对爆破振动效应所带来的安全隐患的重视程度也在不断提高[1]，国内外学者就如何将其影响程度控制在可接受范围内开展了大量研究[2-3]。只有掌握爆破振动传播规律，才能对其影响程度作出准确预测，从而达到有效控制爆破振动的目的。

爆破振动效应具有复杂性、模糊性及不确定性，近年来，学者们对其进行了大量研究并取得了一系列有益成果。焦永斌[4]将频率影响系数与折算振动速度公式相结合，作为爆破地震的安全评定标准。徐光兴等[5]通过振动台模型试验研究，总结出了在地震效应作用下1∶10边坡模型的力学特性和动力响应的一般规律。张义平[6]结合理论研究与实际监测成果，利用Matlab进行数据处理，首次提出爆破振动可用HHT变换理论进行研究的思路。黄光球等[7]运用遗传规划法，以实际数据为基础，阐述了真实经验公式的原理。

本文根据物理量之间的数量关系，利用量纲分析法，从理论上推导爆破振动速度预测模型，再通过回归分析的方法在实际工程中加以验证，最后对比不同经验公式的相对误差，以判别其拟合精度的高低，以期为类似工程及研究提供借鉴。

1 量纲分析法

量纲是物理量的基本构成成分，利用这一基本成分的内在关系，并考虑一切物理量所必须具有的基本形式，就可以将物理量之间存在的数量关系正确地分析出来。在爆破振动问题中，选择3个物理量作为基本量纲，在此基础上，其他的物理量均可用这3个基本量纲表示，组成新的量纲组合形式。这3个基本量纲分别是表示质量的基本量纲[M]、表示时间的基本量纲[T]、表示距离的基本量纲[L]。

分析结果表明，影响爆破振动质点振速的因素有：同段最大装药量Q、爆心距R、爆心与测振点之间的高差H、爆轰时间t、爆炸产生的地震波的传播速度c、岩体密度ρ。共有6个自变量、1个因变量(见表1)。地表岩体质点的振动速度可以表示为

V=f(Q,R,H,t,c,ρ) 。

(1)

表1 爆破振动所含重要物理量

影响爆破振动速度的自变量有6个，取Q、R、c为独立量纲，由布金汉定理可知，n=6,m=3,故有3个无量纲量。π代表无量纲物理量，则有

(2)

(3)

(4)

(5)

式中，α、β、γ为待定系数。以式(1)为例，与π对应的分式上下量纲相等，则有

V=LT-1=(M)α(L)β(LT-1)γ。

(6)

由α=0，β=0，γ=1，可得π=V/c。

同理可以推出：

(7)

将式(2)-式(7)代入式(1)可以得出爆破振动质点振速与上述3个无量纲量存在的函数关系式：

(8)

(9)

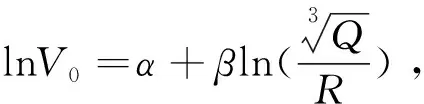
(10)

令eα=K，则式(10)变为

(11)

可以看出式(11)正是传统的萨道夫斯基公式，故将式(11)代入式(9)得

(12)

同理，将式(12)两边取以e为底的指数，并令K=K1，eα′=K2，β=β1，β′=β2，可得

(13)

式中：K1为场地系数，与岩体性质、爆破工艺等因素有关；K2为地形影响系数，与地形地貌有关；β1为衰减系数；β2为高程影响系数[10]；其他参数同前。

2 经典预测模型

目前应用最为广泛的是由萨道夫斯基提出的爆破振动衰减规律经验公式[11]：

(14)

日本学者给出了场地系数的经验公式：

(15)

我国长江科学院提出了考虑以高差作为影响因素的爆破振动速度预测公式[12]：

(16)

式中，L为爆破中心至测振点的水平距离，其他参数同前。

3 工程实例

3.1 工程概况

某隧道工程位于广西某地区，属低-中山地貌，山体地形起伏较明显，多呈“V”形，冲沟坡降较大。隧道出口端的冲沟距沟底约25 m，沟底宽约20 m，两侧分布3～5 m陡坎，沟壁土坎近于直立，其上为陡坡地形，自然坡度20°～30°，多覆盖第四系残坡积层，路面横坡坡度约为2%。其中Ⅲ类围岩占比约为51%，Ⅳ类围岩占比约为34%，Ⅴ类围岩占比约为15%；隧道围岩主要以强-中风化泥岩、砂岩为主。

3.2 爆破参数

因隧道施工工艺所需，要对出口附近某路基进行爆破。爆破区域与测振点之间的高差约为30 m，开挖方式采用深孔台阶爆破法。主要爆破参数为：台阶高度为10 m左右，炮孔深度为10 m(超挖深度h=0.5 m)，炮孔直径D为0.09 m，炮孔间距为3 m，炮孔排距为2.5 m，堵塞长度为3.5 m，最小抵抗线为3 m；第一次同段最大药量为48 kg，第二次为42 kg；采用梅花形布孔，70 mm乳化炸药，数码电子雷管起爆。

3.3 施工方法

(1)路基爆破深孔凿岩设备采用KL511潜孔钻机，钻头直径90 mm。

(2)测量放线后，由技术人员划定开挖边界，再根据现场岩石出露情况，测量并划定炮孔位置，根据开挖高度标定每个炮孔的钻孔深度[13]。

(3)钻凿炮孔过程中，技术人员须对每个炮孔进行核查，发现炮孔偏斜、堵孔等现象时，应立即进行补孔、清孔。

(4)爆破前先清孔，确保孔深达到设计要求。

(5)装药作业

a.炮孔布置完成后开始装药作业，装药作业必须由持证人员操作，施工时除爆破员和爆破工程技术人员外，其他人员禁止进入施工区域。

b.采用人工装药，起爆体、起爆药包应由爆破员携带、搬送。

c.炮孔装药应使用木质或竹制炮棍。

d.不应往孔内投掷起爆药包和敏感度高的炸药，起爆药包装入后应采取有效措施，防止后续药卷直接冲击起爆药包。

e.装药发生卡塞时，若在雷管和起爆药包放入之前，可用非金属长杆处理；装入雷管或起爆药包后，不应用任何工具冲击、挤压。

f.在装药过程中，不得拔出或硬拉起爆药包中的雷管引脚线。

(6)装药结束后，由爆破工程技术人员进行网络连接。将网络按设计逐孔连接，再逐段检查，发现漏接、错接情况时应立即重新连接，确保网络连接正确、完整[14]。

(7)网络连接完成后，必要时在炮孔口压沙袋进行防护。

(8)待所有人员撤离施工场地后开始警戒，警戒时间30 min，爆破警戒范围在爆破区域200 m内。

(9)确认安全后，由现场负责人倒计时，发出起爆信号，由爆破员负责起爆。

(10)爆破完成5 min后，工程技术人员方可进入现场检查，确认安全后才能解除警戒，如发现盲炮等现象，经处理后方可解除警戒。

(11)爆破完成后采用机械工具对松动岩石进行破碎、清理。

3.4 监测方案与监测结果

本次爆破振动监测是实时监测，为确保监测结果准确可靠，应对爆破点附近的监测对象进行详细调查，在爆破前对监测系统进行检查、检测和标定，最后根据监测对象与爆破点相对位置关系确定测点位置及布置方法。

在本次实验中，采用成都中科测控生产的TC-4850智能爆破测振仪。根据现场实际情况，第一次起爆选取4个测振点，分别位于爆区南69 m、西南71 m、西北71 m、东北103 m；第二次起爆选取4个监测点，分别在爆区东108 m、东北121 m、东北135 m、北70 m。监测点处均采用专用的石膏耦合剂使传感器与地基稳固黏结，监测点的仪器安置情况如图1所示，监测结果和各监测点所对应的主要爆破参数见表2。

图1 测振仪器布置情况

表2 爆破振动监测结果

4 回归分析

为解决工程实际问题，常根据变量之间的相互关系，通过分析实测数据，拟合得出能够满足数据关系的数学模型，其中最简单的模型是线性回归分析法对应的线性模型。在大多数情况下，影响爆破振动的各因素与爆破振动峰值速度之间并不符合单一的线性关系，而必须用某种复杂的非线性关系才能将其表征。在处理此类问题时，可采用最小二乘法，结合Newton迭代，遵循非线性残差平方和最小的原则，便可求解出其中的未知参数。

设多元函数V=f(x1,x2,…,xn)的一组测量数据为(x1i,x2i,…,xni,Vi)(i=1,2,3,…,m)，所对应的一组权重系数wi>0，满足函数式(10)，则有

(17)

(18)

在实际操作中采用1stOpt软件计算，以提高计算效率。通过确定自变量、待定参数，建立相应的数学模型，将自变量对应的实测值一一列出等步骤后采用软件求出待定参数值。根据非线性回归分析结果可得出迭代次数、残差平方和、相关系数、决定性系数以及参数k、α的最佳估算值。其中：式(13)中的K1=171.97，K2=0.003 4，β1=-0.782 6，β2=1.607 2；式(14)中的K=150，α=1.519；式(15)中的K=480.44；式(16)中的K1=1.75，β1=0.916，β2=-1.197。将以上参数值代入式(13)-式(16)即可得到以上4种预测模型在该工程背景下对应的具体预测表达式：

(19)

(20)

(21)

(22)

对式(19)-式(22)进行回归分析得到的爆破振动峰值速度预测值以及实际监测值见表3。

由表3可知，式(19)的相对误差平均值为3.24%，式(20)的相对误差平均值为23.84%，式(21)的相对误差平均值为27.68%，式(22)的相对误差平均值为4.82%。由此可知，式(19)即基于量纲分析法推导出的爆破振动速度预测公式的精度最优。

5 结论

a.通过工程应用对比发现，传统的萨道夫斯基爆破振动速度预测经验公式和日本学者给出α系数的经验公式所建立的爆破振动峰值速度预测模型均存在较大误差，不能较好地反映爆破振动波的传播及衰减规律，其相对误差平均值均超过了20%；而基于量纲分析法所推导出的爆破振动速度预测公式，相对误差平均值仅为3.24%，较其他几种经典公式而言拟合精度最优。

b.对于周期性爆破作业环境而言，由于岩体受到多次扰动、损伤，使得爆破振动峰值速度预测模型的参数取值发生变化，从而影响其预测精度，考虑这些因素的预测模型还有待进一步研究。