一类非局部问题非平凡解的存在性

赵 福，宋玥蔷

(长春师范大学数学学院，吉林 长春 130032)

0 引言

本文主要研究一类非局部问题：

(I)

其中，Bε(x)表示RN中以x为圆点、ε为半径的开球，ε>0.

YIN和LIU[1]通过山路引理方法研究了非局部问题(1)的非平凡解的存在性和多解性：

(1)

随后，在问题(1)基础上，LEI等[2]利用变分方法研究非局部问题(2)的具有变号势两个非平凡的正解：

(2)

其中，Ω是R3中的光滑有界区域，N≥1，a,b>0，10，

f±=±max{±f,0}≠0.

QIAN等[3]考虑了下面非局部问题(3)的基态解存在性和集中性：

(3)

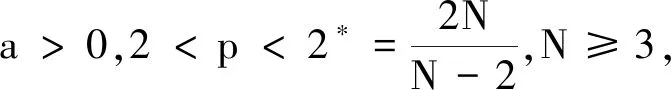
研究此类非局部问题的难点在于非局部项的存在使紧性条件的证明变得困难，分数阶Laplace算子更是加深了变分的难度，我们需要选择更灵活的变分技巧,证明泛函在水平值的控制下满足紧性条件，通过山路定理证得主要结论.

1 预备知识

定义一个Sobelev空间X=Hs(Ω)，s∈(0,1)，其范数为

因此，存在γr>0，使得

(4)

如果有

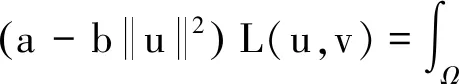
成立，其中，

则u∈X称为问题(I)的弱解.

定义泛函

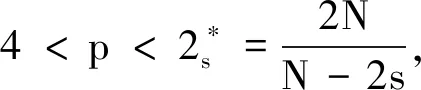
当且仅当u在X上是泛函I(u)的临界点时，称u为问题(I)的弱解.

欲证明定理1，首先要证明(PS)c条件.

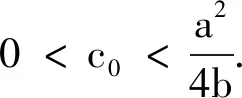
证明 由不等式(1)，有

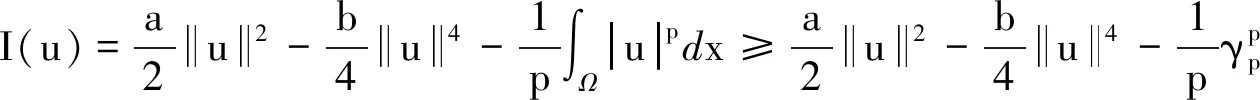
证明 令序列{un}⊂X,满足I(un)→c，I′(un)→0，

因为

I(un)→c，I′(un)→0，所以序列{un}在X上有界.

假定存在u∈X，使得

un→u, 在X中,

un→u, 在Lr(Ω)中,

un(x)→u(x), a.e.x∈Ω.

注意到

因为

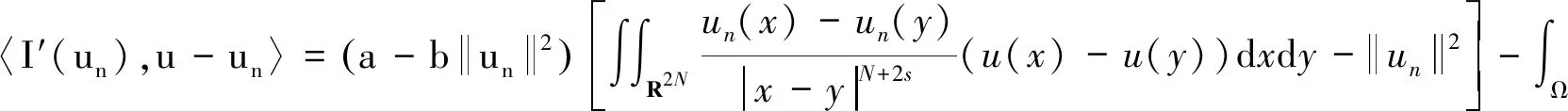
由之前的条件可知〈I′(un),u-un〉→0.

所以有

(5)

定义泛函

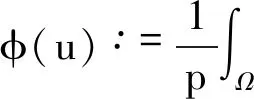
有

由Holder不等式，有

因此，

则有φ′(un)→φ′(u).

而且

所以，φ′(un)→0,n→∞，即

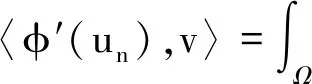
从而，u=0.所以，

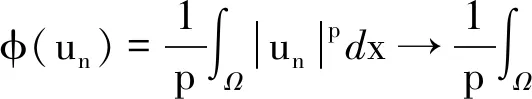
2 主要结论及证明

利用山路定理，给出定理1的证明.

定理1 问题(I)至少有一个非平凡的弱解.

证明 由引理1，存在序列{un}⊂X，满足I(un)→c0>0，I′(un)→0,n→∞.由引理1和引理2得到的序列{un}具有一个收敛子列(仍然定义为{un})，并且收敛于u.所以，由I和I′可知，I(u)=c0>0，I′(u)=0.但是I(u)=0，因而u≠0，u是问题(I)的一个非平凡解.