图的覆盖数与分子的凯库勒结构
胡启明,许 欢,袁晓彤
(合肥幼儿师范高等专科学校公共教学部,安徽 合肥 230013)
0 引言



图1 G1


图2 G2
求图的最小顶点覆盖被称为顶点覆盖问题(vertex cover problem,VCP),VCP是理论计算机科学和离散数学中一个经典NP完全问题,可追溯到20世纪30年代Konig的经典结果[1].1972年KARP[2]证明了VCP对于一般图是NP完全的.求图的最小边覆盖被称为边覆盖问题,该问题是由RABIN[3]首先提出的.边覆盖在交通相位问题中起着重要的作用,可应用于网络分析.到目前为止,只有Mangoldt图得到了最小边覆盖[4].
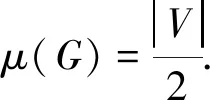
不失一般性,将化学分子结构看成一个图,其顶点对应于化合物的原子,边对应于隐藏于化合物中的化学键,称之为化学图.多数情况下,化学图的顶点度都小于或等于4.化学图论是数学化学的一个分支,化学图论模型已被广泛应用于预测化合物的性质[5].在过去几十年里,学者们对化合物凯库勒结构的研究积累了许多成果[6-7].
有凯库勒结构的化学分子,相当于含有完美匹配的化学图[8].若一个图含有完美匹配,则称它为凯库勒图.从图论观点看,凯库勒图是一个有趣问题,如果不分析覆盖数,这个问题将是未知的.部分学者对凯库勒结构进行了大量的研究[7-8],但尚没有将覆盖数与凯库勒结构联系在一起的研究.在化学图中,使覆盖问题有意义的,是它与凯库勒结构的紧密联系.因此,本文将讨论图的覆盖问题,并用覆盖数刻画感兴趣的化学图,通过计算一些特殊图的点覆盖数和边覆盖数,来刻画覆盖数和凯库勒结构的相关性.
1 凯库勒图的充要条件
定理1.1 设G=(V,E)是二部图,则图G是一个凯库勒图⟺β(G)=β′(G).
证明 “⟹”假设图G是一个凯库勒图.


“⟸”假设β(G)=β′(G).

2 因子临界图
近似完美匹配,是指图中存在只剩下一个顶点未被包含的最大匹配.若对于图中每个顶点都有一个近似完美匹配,则称该图为因子临界图.也就是说,如果去掉因子临界图中的任何一个顶点,它就变成了凯库勒图.
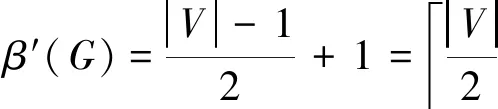


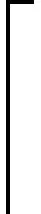





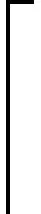







3 顶部梯状图
如图3所示,把顶部梯状图记为TLn,n≥0,它们有顶端a和基对b1,b2,与顶端a相邻的两条边称为图的顶部,连接基对的边称为图的底部,由底部向下添加梯级(2个顶点、3条边)构成梯形图.
例如,TL0(即完全图K3)可指定其任一个顶点为顶端,其余两个顶点为基对;又如,TL1(类似于房屋图)是一个含有5个顶点和6条边的简单图.一般地,任一顶部梯状图TLn,n≥0,都有2n+3个顶点和3(n+1)条边.这类图包含近似完美匹配,即顶部梯状图都是因子临界图.

(a)TL0 (b)TL1 (c)TLn图3 顶部梯状图
定理3.1 若G是一个顶部梯状图TLn,则β(G)=n+2,n≥0.
证明 用数学归纳法,
当n=0时,G为TL0是K3,此时,β(G)=β(TL0)=2=0+2;
当n=1时,G为TL1是房屋图,此时,β(G)=β(TL1)=3=1+2;
假设当n=k时,结论成立,即有β(TLk)=k+2,下面证明n=k+1的情况.
由顶部梯状图的构造易知,TLk+1是在TLk基础上增加了2个新顶点和3条新边.显然,只要在TLk的覆盖里添加1个新顶点即可得TLk+1的一个覆盖.则有β(TLk+1)=β(TLk)+1.从而β(TLk+1)=k+3=(k+1)+2.
因此,对于所有的n≥0,都有β(G)=B(TLn)=n+2.
定理3.2 若G是一个顶部梯状图TLn,则对于所有的n≥0,都有β′(G)=β(G).
证明 设G(V,E)是一个顶部梯状图TLn.
4 广义梯形图
设TLn1和TLn2是两个顶部梯状图(两边的梯级数即梯形图的尺寸分别为n1和n2),连接TLn1和TLn2的两个顶端点构成边(称之为桥),产生的新图记为L(n1,n2). 此类图含有完美匹配,即为凯库勒图.
以L(n1,n2)的桥的两个顶端点为基对再构造n3个梯级,记为L(n1,n2,n3).易知,这一类图含有完善匹配.分别连接L(n1,n2)中的TLn1和TLn2两组基对点构成边(称之为悬挂边),这样产生的新图记为L(n1,n2,M).
不失一般性,在顶部梯状图的顶端和基部分别构造桥和悬挂边,产生的图(图4)记为L(n1,n2,n3,M),称为广义梯形图.

图4 L(n1,n2,n3,M)
定理4.1 设G=L(n1,n2,n3,M),则对于任意的n1≥0,n2≥0和n3≥0,都有β(G)=n1+n2+n3+4.
证明 分情况讨论,
(1)若n1=n2=n3=0(图5),图G中含有2个三角形、2个悬挂边和1个桥,则需要从每个三角形中各选择2个顶点来覆盖图中的9条边.此时,β(G)=2+2=4.

图5 L(0,0,0,M)
(2)若n1=n2=0,n3≠0(图6),则需要n3个顶点覆盖尺寸为n3的梯形图,需要4个顶点覆盖2个三角形、2个悬挂边和1个桥.此时,β(G)=n3+4.

图6 L(0,0,n3,M)
(3)若n1=n2≠0,n3≠0,则分别需要n1,n2和n3个顶点覆盖图G中3个梯级.同时,图G中含有2个三角形、2个悬挂边和1个桥,需要4个顶点来覆盖.此时,β(G)=n1+n2+n3+4.
(4)若n1≠n2≠0,n3≠0,当n1
定理4.2 设G=L(n1,n2,n3,M),则对于任意的n1≥0,n2≥0和n3≥0,都有β′(G)=n1+n2+n3+3.

因为G=L(n1,n2,n3,M)含有完美匹配,所以,

