改进的并查集迷宫地图生成算法研究与设计

史宝明，贺元香，马少斌

(兰州文理学院数字媒体学院，甘肃 兰州 730010)

0 引言

迷宫存在的历史已经有5 000多年，最早可以追溯到古希腊的神话传说。迷宫不仅在现实生活中比较常见，而且在计算机游戏中也有很广泛的应用[1-3]，游戏中的迷宫可以通过手工绘制或建模的方式生成，也可以通过设计迷宫生成算法自动生成，游戏中的迷宫地图可以极大地增强游戏的趣味性，提升游戏的吸引力。一般而言，迷宫有单迷宫和复迷宫之分，单迷宫是指只有一种走法的迷宫，可沿着某一面墙壁走，用左(右)手始终摸着左(右)面的墙壁，就一定可以走出迷宫。复迷宫是指有多种走法的迷宫。在复迷宫中如果存在一些路径可以不回头地走回原点，则以这条闭合的回路为界，复迷宫可以被划分为多个部分，因此复迷宫可看作由多个单迷宫组合而成。

迷宫地图在计算机游戏中有着广泛的应用，可以通过特定的算法来随机生成迷宫地图，当游戏角色在迷宫场景中随机游走时[4]，可以极大地增强游戏的趣味性和吸引力。迷宫的生成算法多种多样，典型的生成算法主要有深度优先搜索算法[5]、随机Prim算法[6]、递归分割算法[7]、并查集算法[8-11]等。并查集(Union-Find Sets)是一种树型的数据结构，主要用来处理不相交集合的合并及查询问题，在任务规划求解[8]、聚类分析[9]、机器视觉检测[10-12]等领域有着广泛的应用，以下着重研究使用并查集算法生成迷宫地图。

1 并查集

1.1 并查集算法

并查集是一种应用广泛的集合，由若干不相交的子集合组成，并查集算法主要包含并(Union)操作和查(Find)操作。

Find(a)：判断元素a属于哪一个子集，即在一个集合树中不断向上查找到它的根结点并返回。这个操作可以判断两个元素是否属于同一个子集，即判断根结点是否相同。

Union(a,b)：将元素a所在的集合和元素b所在的集合并为一个集合。

除了这两个操作，还有建立单元素集合的操作(MakeSet)，通过这些操作可以解决实际中经常碰到的规划问题、聚类问题、迷宫生成问题等。并查集通常采用树形结构来存储数据，每个元素中都存储其父元素的地址信息，下面通过图1和图2演示并查集的操作过程。

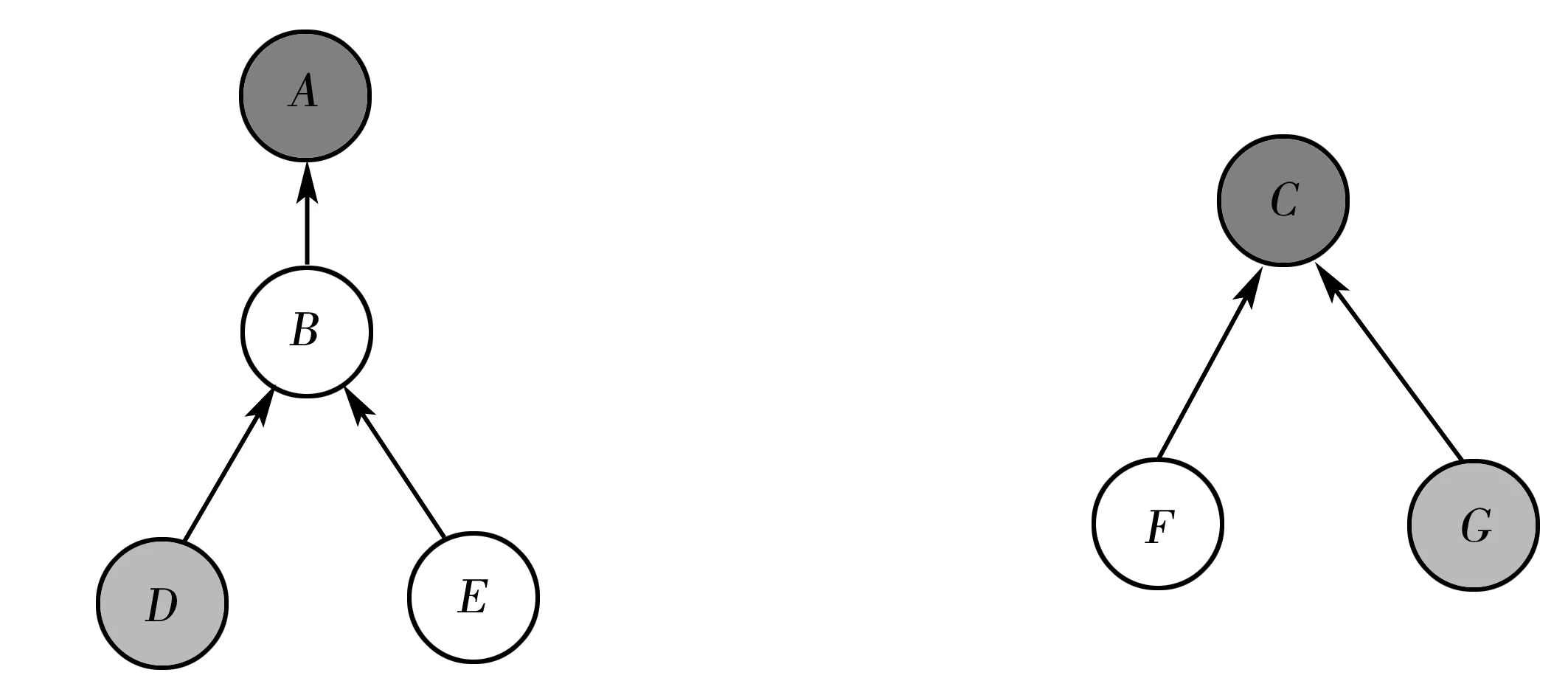
(a)子集一 (b)子集二图1 两个并查集子集

(a)C接A (b)A接C图2 执行并操作

在图1中，对于D和G两个元素，判断它们是否连通，即是否属于同一个集合，可按如下方法进行：对于元素D和G执行查操作Find(x)，返回对应元素的根结点，即有Find(D)的值为A，Find(G)的值为C，发现两个根元素不相同，可知D和G属于两个不同的子集，此时表明这两个子集是不连通的。若希望D和G连通时，就需要执行并操作，即将G的根C接到D的根A上，如图2(a)所示，此时树的深度为3，或将D的根A接到G的根C上，如图2(b)所示，此时树的深度为4。子集连接的选择，对整个算法的性能有很大的影响，可采取如下策略对并查集算法进行优化。

1.2 优化方法

在执行并操作时，如果不注意连接方式，就有可能导致连接后的树出现不平衡的现象，如图2(b)所示，进而导致查找过程变慢。解决的办法有两钟：一种方法是按秩合并；另一种方法是采用路径压缩来优化集合树。

1.2.1 按秩合并

这里的秩指的就是树的深度，按秩合并即记录每个子集树的深度，当执行两个子集树的并操作时，选择始终将深度小的树的树根接到深度大的树的树根上，如图2(a)所示，即将深度小的树C接到深度大的树A上，树的深度不变；若两个树的深度大小一样，则可任意合并，合并后的树的深度加1。按秩合并可以让集合树尽可能地保持相对平衡，进而可以提升查找效率。

1.2.2 路径压缩

路径压缩是一种在执行“查”操作时扁平化树结构的方法，即在递归的查找树的过程中，将每一个结点的父结点直接设置为根结点(图3)，这样可让查找效率大大提升。路径压缩的思想着重关注每个结点的父结点，而无需关注树的结构，这个方法不仅极大地优化了“查”操作，同时也优化了“并”操作，可使并查集算法的效率大大提高。

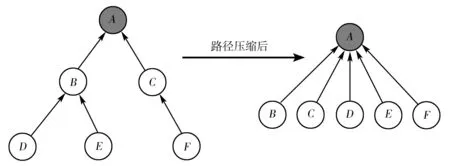
图3 路径压缩

2 改进的并查集迷宫生成算法

2.1 迷宫初始化

当设定好一个m行n列的迷宫时，考虑墙体在内则需要一个2m+1行2n+1列的矩阵Maze[2m+1,2n+1]来进行迷宫的初始化。假设行列的序号都从0开始，则一个迷宫空间可被偶数行和偶数列墙体划分为一个一个的小单元。一个2m+1行2n+1列迷宫矩阵的初始化过程如下：

for (i = 0; i < 2*m+1; i++)

for (j = 0; j < 2*n+1; j++)

{

if (i == 0 || i ==2*m || j == 0 || j ==2*n)

maze[i,j] = 1; //迷宫外墙设置

else if (i % 2 == 0 || j % 2 == 0)

maze[i,j] = 1; //迷宫中间墙设置

else

maze[i,j] = 0; //迷宫单元格设置

}

Maze[i,j]的值为1表示墙体单元格，为0表示迷宫单元格。一个3×3迷宫的初始化状态如图4(a)所示，其中，黑色单元格为永久性墙体，网格状单元格和斜线单元格为可拆除墙体，白色单元格为迷宫单元格。如果墙体单元格用1表示，迷宫单元格用0表示，则可得到图4(b)所示的一个二维01矩阵。将墙体简化为线条后的迷宫如图4(c)所示。

(a)初始化 (b)数据化 (c)墙体简化为线条

2.2 迷宫生成

迷宫生成的基本思路是在已初始化的迷宫矩阵中先设定起点和终点，并将可拆除的墙(即图4(a)中的网格墙和斜线墙)放入一个列表，然后循环从列表中不断随机选择一面墙，判断被墙分隔的两个迷宫单元是否连通，若不连通就拆掉该墙，并将该墙从列表中移除，重复此过程直到起点和终点连通为止。在迷宫生成的过程中，执行并查集算法中的并操作时，采用按秩合并的策略进行，在执行查操作之前，先对集合树进行路径压缩处理。整个迷宫生成的算法设计如下：

Step1 在迷宫中选定起点a和终点b；

Step2 将网格墙和斜线墙单元格结点信息放入列表list中；

Step3 随机从list中取出一面墙，对该墙两侧的单元格结点分别执行“查”操作，查找其根结点；

Step4 判断两个结点的根结点是否相同，若不相同，执行“并”操作，打通墙，并将此墙移出对应列表；

Step5 对起点a和终点b分别执行“查”操作，判断其是否连通，若不连通，跳转到Step3继续，否则算法终止。

在每次执行“并”操作时，使用按秩合并的方法进行集合树的合并，在执行“查”操作时，先采用路径压缩的方式对集合树进行扁平化处理，再进行查找，可以极大地提高查找效率。上述算法结束的条件是起点和终点连通，此时迷宫中有些单元格可能还未访问到，这会导致有些迷宫单元格永远都到达不了的情形出现，若希望能够到达迷宫的任意单元格，则只需将算法结束的条件更改为列表list为空即可。

3 算法仿真及结果分析

3.1 实验环境

实验仿真的计算机型号为Lenovo启天M6600，操作系统为Window10(64位)，处理器为Intel®CoreTMi5-6500 CPU@3.20 GHz，测试软件为Visual Studio 2017，算法用C#编程实现。

3.2 迷宫地图生成仿真

迷宫生成程序使用C#语言实现，使用并查集算法思想先生成迷宫矩阵，再根据迷宫矩阵来绘制迷宫地图。

设定迷宫格为15×15，则对应的迷宫矩阵为31×31，迷宫单元格之间的墙体采用线条来进行绘制，设定迷宫的起点为最左上的单元格，终点为最右下的单元格，则当起点连通终点时，运行3次程序生成的迷宫，如图5所示。

(a)第1次 (b)第2次 (c)第3次图5 起点连通终点时生成的迷宫

由图5可以看出，每一次运行生成的迷宫均不相同，在3次生成的迷宫地图中，均存在一些封闭的迷宫单元格,四面都有墙体，在这样的迷宫中行走时，这些封闭的迷宫单元格是无法访问到的。将迷宫生成的终止条件变更为遍历到每一个迷宫单元格，再运行程序，运行3次后得到的结果如图6所示。

(a)第1次 (b)第2次 (c)第3次图6 遍历所有单元格后生成的迷宫

由图6可以看出，3次运行结果中均不存在不可访问的迷宫单元格，此时从迷宫中任意一点出发，都可以遍历所有的迷宫单元格，这也是在实际中应用较为广泛的一种迷宫。

3.3 算法结果分析

以上使用并查集思想设计的迷宫生成算法在生成迷宫时，只需要控制一个二维矩阵中矩阵元素的01变化即可，在迷宫初始化时，通过双重循环来设置矩阵元素，时间复杂度为O(n2)，使用并查集算法生成迷宫时，时间主要消耗在“查”操作上，如果对查找的树采用了路径压缩，则可将“查”操作的时间复杂度由O(n)提升为O(1)。在遍历迷宫单元格时，只需一个while循环作为遍历结束的终止条件，其时间复杂度为O(n)，并且可通过控制结束条件来生成不同类型的迷宫。总地来看，使用改进的并查集算法生成迷宫地图时效率较高，生成的迷宫地图结构布局合理，适合在各种迷宫探索游戏中进行部署和应用。

4 结语

本文设计并实现了基于并查集思想的迷宫地图自动生成算法，通过按秩合并、路径压缩等方式对迷宫生成算法进行了优化，算法设计高效，可以应用在各类游戏开发中。除了文中探讨的并查集迷宫自动生成算法外，研究如何将深度优先搜索算法、Prim算法、递归切割算法应用在迷宫地图的生成中并加以改进，如何在生成好的迷宫地图中进行高效的智能寻路，是今后课题研究的重点方向。