立足数学思想 发展核心素养
——2021 年新高考Ⅰ卷第19 题的探究与反思
江西省萍乡市萍乡中学 黄贤锋 (邮编:337055)
解三角形是高考的重点热点问题,主要考查学生的基础知识及基本技能. 这类问题通常蕴含着丰富的数学思想,着力考查学生数学抽象、逻辑推理、数学建模等核心素养. 2021 年新高考Ⅰ卷第19 题就是具备以上特点的一道好题.
1 真题呈现
记△ABC的内角A、B、C的对边分别为a、b、c.已 知b2=ac,点D在 边AC上,BDsin ∠ABC=asinC.
(1)证明:BD=b;
(2)若AD=2DC,求cos ∠ABC.
2 考情分析
6 月9 日晚,笔者组织2022 届两个理科零班共102 人对本套试卷进行了测评,发现试卷的19题(以下简称真题)第(2)问的答题情况很不理想. 该题的平均分为7.14 分,满分人数仅为26.通过阅卷及后期座谈收集到学生在处理第(2)问时主要存在以下几种类型的问题:
类型1对题型感觉陌生,题中没有给出任何边长与角度的信息,感觉无从下手;
类型2得到两个关于a、b、c及角度的方程,利用b2=ac,消元后仍有三个未知量,但是只有两个方程,无法解出自变量;
类型3由∠ABC=∠ABD+∠CBD,想通过两角和的余弦公式进行求解,陷入困境.
针对以上考情,从真题溯源,解法剖析,变式拓展等几个方面对真题进行探究,并对解三角形专题的复习备考进行反思. 以期提升学生的数学能力,发展学生的数学核心素养.
教材与历年高考试题凝结了专家的智慧,是高考命题的重要素材,更为广大师生备战高考指明了方向. 很多高考题都能在教材中找到原型.
3 真题溯源
母题1[1]△ABC的三边之比为3∶5∶7,求这个三角形的最大角.
母题2 (2015 年全国Ⅱ卷 理17 题)ΔABC中,D是BC上的点,AD平分∠BAC,ΔABD面积是ΔADC面积的2 倍.
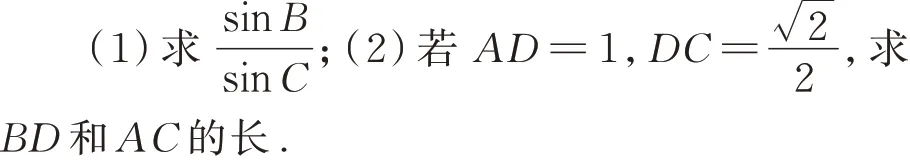
评注母题1 揭示了通过三边的比例关系可求三角形任意角的余弦值的事实. 结合b2=ac,故只需寻找两边边长的比例关系即可,为解决真题提供了方向. 真题是母题2 的升级,其中ΔABD面积是ΔADC面积的2 倍,等价于AD=2DC. 区别在于母题的第(2)问是已知边长求边长,而真题的第(2)问是已知边长关系b2=ac,BD=b,AD=2DC,求角的余弦值.
4 解法剖析
方向1利用互补两角的余弦值和为0
解法1 由余弦定理得AB2=BD2+AD2-2BD·AD·cos ∠ADB,
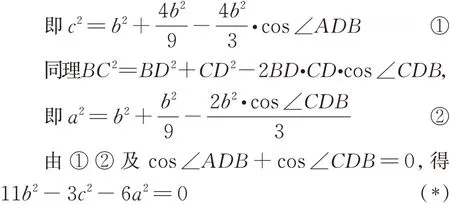

解法2易知∠ADB、∠CDB均不为直角,由三角形面积公式及余弦定理得

解法3如图1,过点D作AB的平行线交BC于点E,易知
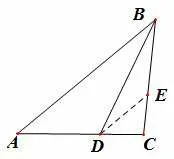
图1
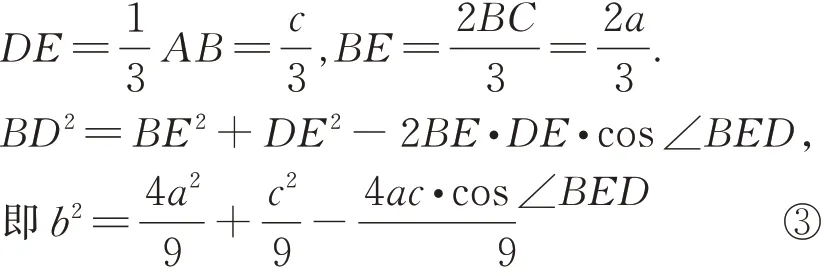
又由余弦定理知
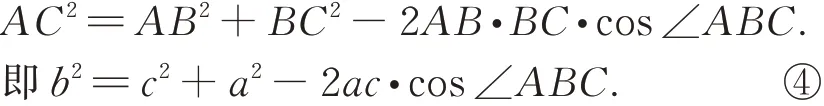
由③④及∠ABC+∠BED=π,得(*)式,下同解法1.
方向2利用同一个角“算两次”

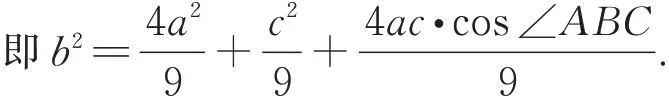
结合④式可得(*)式,下同解法1.
解法5在ΔABD、ΔABC中使用余弦定理得
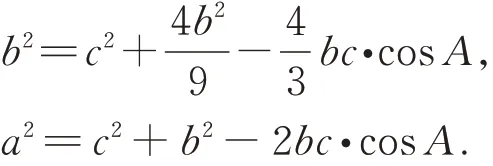
由以上两式消去cosA,得(*)式,下同解法1.
解法6在ΔCBD、ΔABC中使用余弦定理得
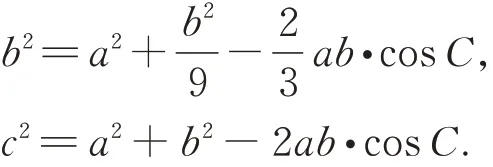
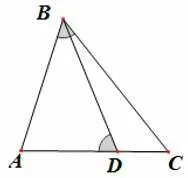
图2
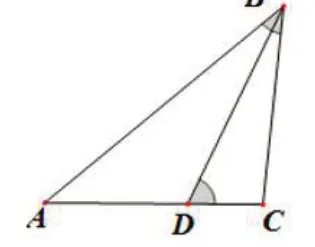
图3
由以上两式消去cosC得(*)式,下同解法1.
方向3利用平面几何性质
解法7

解法8由斯特瓦尔特定理知,AB2·CD+BC2·AD-BD2·AC=AD·CD·AC. 整理得(*)式,下同解法1.
解法9如图4,延长BD交ΔABC外接圆于点E,连接AE、CE,由托勒密定理(圆内接四边形对边乘积之和等于两对角线乘积)知,
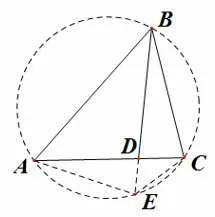
图4
AB·CE+BC·AE=AC·BE.
整理得(*)式,下同解法1.
评注解法1,2,3 关注两角互补,分别使用余弦定理,利用互补的两角的余弦值和为0 进行消元,得到关于a、b、c的方程. 有了以上的认识,自然会想到选择同一个角利用“算两次”思想(也称Fubini 原理)进行消元,于是就有解法4,5,6,其中解法4 使用了向量方法,这是处理这类AD=λ·DC型问题的常见手法. 可以发现在本题的情境下,解法5,6 更为简洁. 解法7,8,9 充分利用了平面几何性质,其中解法7 利用三角形相似. 解法8 用到的斯特瓦尔特定理是对解法1 的一般化. 又注意到斯特瓦尔特定理与托勒密定理是等价的,故有解法9.
可以发现,真题蕴含着丰富的数学思想,如转化与化归思想、整体思想、数形结合思想、方程思想、分类讨论思想、“算两次”思想等,很好地考查了学生的数学抽象、逻辑推理、数学建模等核心素养.
5 变式拓展

评注变式1 基于“算两次”的思想,考查互补两角余弦值和为0 的基础知识;变式2 与变式3基于几何模型AD=λ·DC,可以很好地丰富此类问题的解法.
结合对真题的探究,对解三角形专题的复课备考有如下反思与建议:
6 反思与建议
6.1 回归教材 研究真题
高考试题的命制有“源于教材,高于教材”的特点,很多高考题都有教材例题或习题的影子,如母题1. 只是在呈现方式、问题情境上加以整合、创新. 因此,用好教材对高考的复习备考显得尤为重要. 一方面,学生要对教材上的数学知识做到全面覆盖. 另一方面,教师应积极引导学生对教材中一些有价值的问题进行自主探究,领悟问题的本质. 高考是教学的指挥棒,其命题趋势通常引领着教学方向. 因此,研究真题,洞悉高考试题的命题规律与特点,进行针对性地选题和训练可以提高高考备考的有效性.
6.2 注重落实“双基” 积累思维经验
解三角形主要考查学生利用基础知识和基本技能解决实际问题的能力,其中正、余弦定理是考查的重点. 要求学生能准确地记忆三角公式,熟悉公式的来龙去脉及推导过程,熟练把握公式的各种变形以及适用范围. 在解三角形问题中,要求学生掌握常见的基本技能,如对结构进行等价代数变形、应用消元法解方程组、应用基本不等式求最值等. 教学中要尊重学生的主体地位,重视思维经验的积累. 尽可能地组织、引导学生自主做题、讲题、研题、谈困难、谈想法、谈体会. 使学生积累遇复杂题不慌张,遇简单题不大意的思维经验,真正做到以不变应万变.
6.3 立足数学思想 发展核心素养
数学思想是分析、处理和解决数学问题的根本想法,是对数学规律的理性认识. 也是数学知识到数学素养的桥梁. 如果说数学知识是血肉,数学思想就是灵魂. 史宁中教授认为数学思想本质上有三个:抽象,推理,模型.[2]六大核心素养(数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析)的前三个就是数学基本思想.[3]因此,数学思想是数学核心素养的重要组成部分. 在教学中,教师应引导学生利用数学思想将单个知识点串成线,织成网,形成数学思想的升华. 充分发挥数学思想的统帅与引领作用,发展学生的数学核心素养.

