任凭题目多变化 一个法则贯始终—— 以“三角形中线问题”解题教学为例

福建省福清第一中学 郭海萍 （邮编：350300）

福建省福清市教师进修学校 林新建 （邮编：350300）

数学题目变化多端，但都有既定法则可寻，“万变不离其宗”，教师应引导学生从解题中提炼规律，识破其“宗”“以不变应万变”，以有效应对层出不穷的题目．

下面以一道教材习题为例，就解题教学中如何把握知识本质和学生认知，以有效解决问题作一探析，以飨读者．

试题呈现（普通高中教科书数学必修第二册（人教A 版）习题6.4 第15 题）

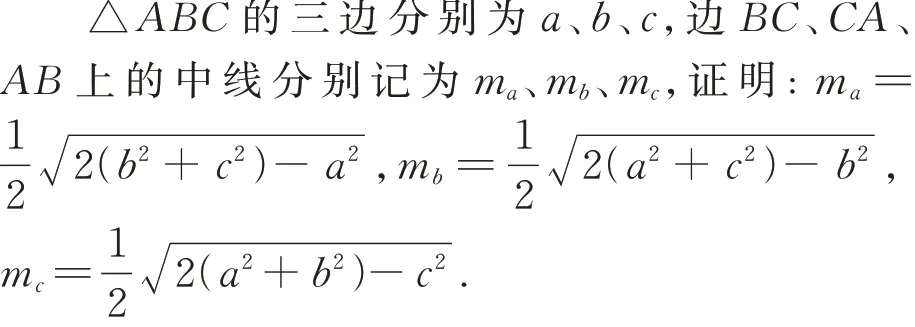
1 解法探析

解三角形中经常会涉及中线问题，这类问题除了需要掌握中线的相关知识外，其本质上是解多个三角形的问题，需要思索怎样将题目中的元素进行整体考虑，将中线长与三角形的边角建立联系，进而将问题得以求解．

解法一运用余弦定理，同角算两次

设AD=x，在△ABC中，

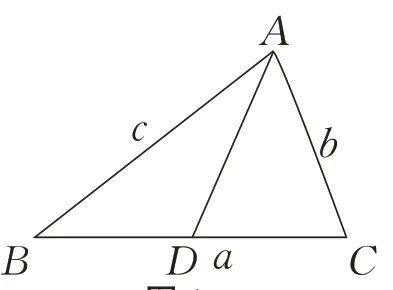
图1

在△ABD中，

由cos ∠ABC=cos ∠ABD，得

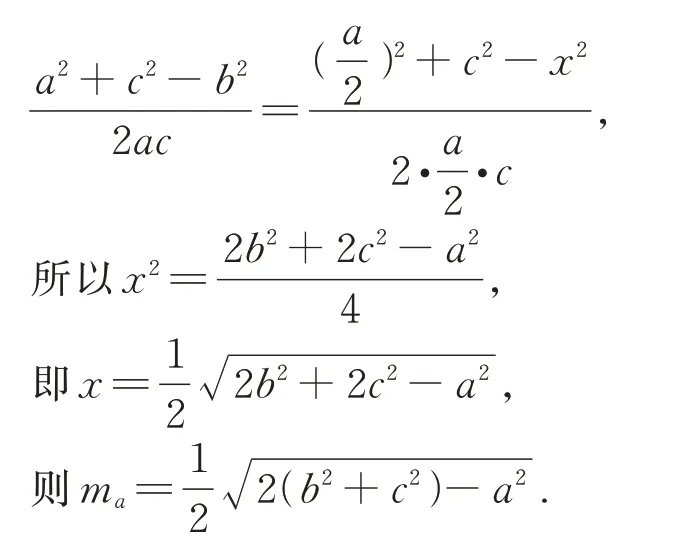
评析解三角形问题的基本方法是“知三求三”，即需要三个量以求出另三个量．把同一个角B放在两个不同的三角形中，利用余弦定理，先 在△ABC中 求 出cos ∠ABC值，再 在△ABD中求出cos ∠ABD值，构建方程求出AD．

解法二运用余弦定理，邻角互补求解

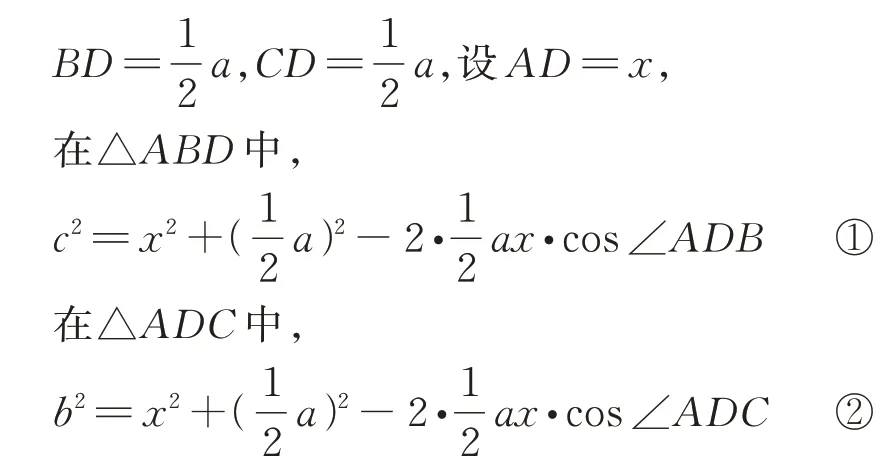
由∠ADB+∠ADC=π，得cos ∠ADB+cos ∠ADC=0，

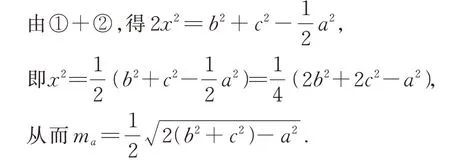
评析根据余弦定理，利用邻角互补，构建方程，算出AD的表达式．

解法三运用基底法则，将向量分解，数量积求模

2 方法剖析

以上三种方法既归纳了求解三角形中线问题的一般方法，又在求解过程中巩固了“余弦定理及其推论”“向量运算”等知识. 数学解题思路和方法灵活多变，不能仅仅满足于解答结果，还要重视对解法的反思，找出解题规律，以理解问题本质，从而提高解题效率．

方法一和方法二立足于解三角形的通法“知三求三”，让学生聚焦三角形，用好正、余弦定理解决问题，难点在于通过“算两次”构造方程，学生往往由于缺乏方程思想引领，不易想到如此方法．方法三立足于向量的应用，通过平面向量基本定理和基底法则将问题得到有效解决．

上述哪个方法比较好呢？显然，从向量的视角运用“基底法则”更具普遍意义，三角形中线问题就是涉及边角关系，而向量运算尤其是“基底法则”就能直接建立起长度、夹角和待求量之间的关系．

3 应用赏析

许多三角形中线或任意分线问题在形式上尽管不同，但却可将其归到同一类型上，我们应将形异质同的问题进行归类，探求问题的本质，探索解题规律，力求以例及类、以点带面．运用向量“基底法则”，可有效解决与之相关的一类问题．

试题结构如：设△ABC的角A、B、C所对的边分别为a、b、c，问题的条件或结论常涉及的量有：(1)点D在边BC上，且的长度；(3)角∠BAC；(4)△ABC的面积或周长等．

题1如图2，设△ABC的角A、B、C所对的边分别为a、b、c，点D在边BC上，且若b=求cos ∠BAC．

题2（2021 年高考数学全国Ⅰ卷第19 题）

记△ABC是内角A、B、C的 对边分别为a、b、c，已知b2=ac，点D在边AC上，BDsin ∠ABC=asinC．

(1)证明：BD=b；

(2)若AD=2DC，求cos ∠ABC.

解析(1)略；

(2)题设条件已知“三边关系式及分线长”，结论求“夹角”，仍可选取恰当基底，建立条件与结论之间的联系，进而求解．

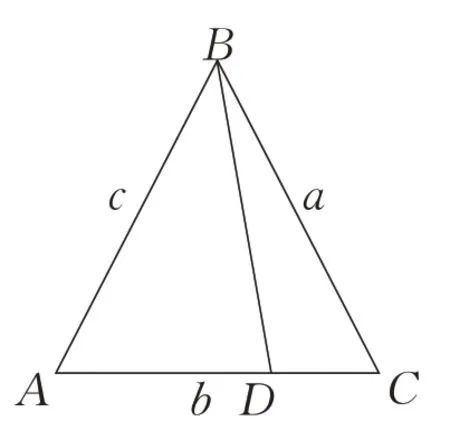
图3

题3（福建省厦门市2022 届高三毕业班3月第二次质量检测数学试题17）△ABC的内角A、B、C的对边分别为a、b、

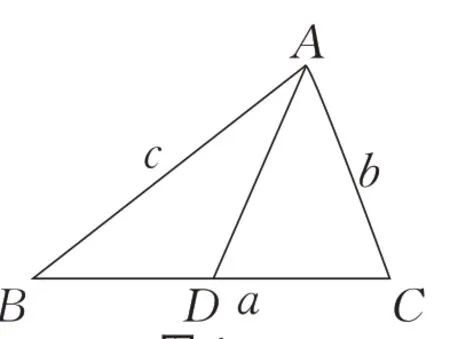
图4

(1)求A；

(2)若a=2，D为BC的中点，AD2=AB·AC，求△ABC的面积．

解析(1)易得

(2)已知“一边及其对角、中线与两边关系式”，结论求“面积”，仍可选取基底，建立条件与结论之间的联系，进而求解．

题4（2015 年高考数学全国Ⅱ卷理科第17

题）△ABC中，D为BC上的点，AD平分∠BAC，△ABD面积是△ADC面积的2 倍．

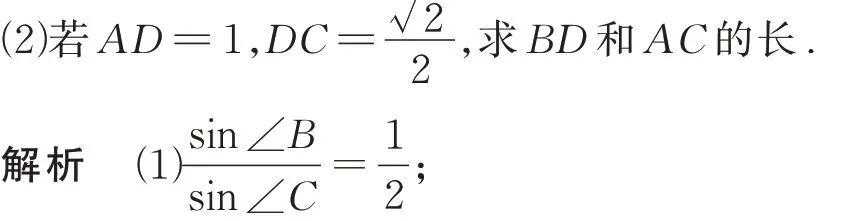
4 素养综析

在上述解题教学活动中，学生经历问题的感知、辨析、提炼等认知活动，使得学生对题设的条件和结论的结构特征进行充分思考，理解问题的本质，将问题转化并解决．在这当中，学生“从数量与数量关系中抽象出一般规律和结构”，进而“借助图形直观分析问题，从特殊到一般地归纳，从一般到特殊地推理”，较好培养和发展学生的数学抽象、直观想象和逻辑推理等核心素养．

因此，解题教学中教师应帮助学生理解知识本质，进行模型建构，获得策略性方法，并引导学生对解题进行深入反思，使学生对数学问题的本质理解更加透彻，同时也能对问题中所蕴含的数学思想体会更加深刻．