基于框架分析法的波形钢腹板箱梁横向内力研究

王永江，曲天岩

（兰州交通大学 土木工程学院，甘肃兰州 730000）

0 引言

波形钢腹板组合箱梁是一种较为新型的组合箱梁结构,在构造上是将传统混凝土箱梁中的混凝土腹板替换成波形钢板。 与传统的混凝土箱梁相比，波形钢腹板具有缩短工期、降低成本等优点，引起世界各国学者的广泛关注。目前国内外学者对波形钢腹板组合箱梁的抗弯、抗剪、抗扭、动力等力学性能的研究比较成熟,但对波形钢腹板组合箱梁横向受力方向的研究相对欠缺[1-5]。 袁亚卓等[6]基于弹性薄板理论，结合波形钢腹板组合箱梁结构受力特性，将组合箱梁的框架展成四跨连续薄板与一边简支、三边固定的薄板后，推导了波形钢腹板箱梁横向内力计算公式。戴慧娟等[7]推导了波形钢腹板组合箱梁桥的横向内力计算公式。赵品等[8-9]基于框架分析法研究了波形钢腹板桥面板横向内力，认为线刚度比是影响箱梁横向内力的重要因素。 郭金琼等[10-11]对带伸臂的普通混凝土组合箱梁桥横向内力进行了研究。 本文利用框架分析法，通过推导虚设侧向水平支撑与无侧向水平支撑时波形钢腹板的横向内力计算公式，研究侧向水平支撑对最终横向弯矩的影响。

本文在分析波形钢腹板组合箱梁横向内力前，为方便计算与分析，对受力模型作出以下假设：（1）组合箱梁截面周边不可压缩；（2）组合箱梁横截面自身平面内服从“拟平截面假定”；（3）翘曲正应力与剪应力沿壁厚均匀分布，即忽略板厚对翘曲的影响。

1 施加虚设支撑的框架分析

波形钢腹板一个波长范围内的形状如图1 所示，其中θ 为波形钢腹板波折角，hc为波高，Lb为倾斜段的水平投影长度，q 为波长，Lc为平直段长度。 波形钢腹板横向抗弯惯性矩为Ic。 组合箱梁横截面如图2 所示。

图1 波形钢腹板形状

图2 组合箱梁横截面简图

利用框架分析法原理，沿组合箱梁桥纵桥向施加虚设支撑和竖向偏心荷载，截取单元长度闭合框架计算支反力，用结构力学方法计算横向弯矩。 再释放施加的刚性支撑，将支反力反向施加在组合箱梁角点处，计算由畸变产生的横向弯矩，由此产生的横向弯矩与施加刚性支撑产生的横向弯矩叠加即为箱梁最终横向弯矩。

利用框架分析法分析单箱室组合箱梁横向内力时，图3 只在底板施加刚性支撑，图4 除在底板施加刚性支撑外，还在角点B 处施加侧向水平支撑，此时组合箱梁在荷载作用下无侧移。 本文将对两种荷载施加形式下的横向内力进行对比研究。

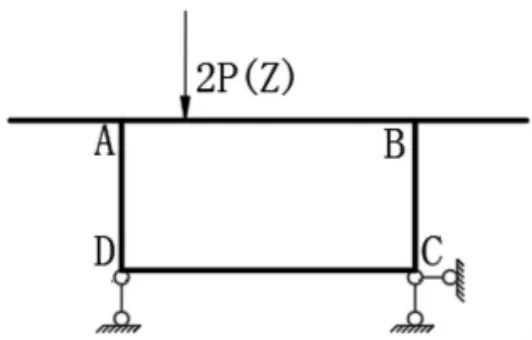
图3 虚设竖向支撑

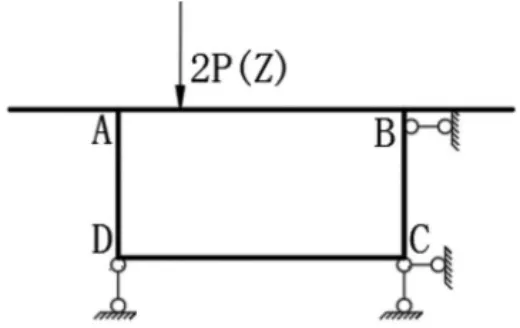
图4 虚设水平和竖向支撑

2 释放虚设支撑的框架分析

本文重点研究释放支撑后的框架分析。 当框架撤出支撑后，在角点处加上与支反力大小相等、 方向相反的力，将该力分解成正对称荷载和反对称荷载，qh为反对称荷载分解的竖向力，qs为反对称荷载分解的水平力。 当采用图3 所示计算模型时无水平力qs，且竖向力的大小qh与图4 计算的值不同。 反对称荷载作用于组合箱梁会产生扭转与畸变，并产生畸变横向弯矩，通过框架畸变剪力差与内剪力的关系可得到横向内力（图5）。

2.1 畸变与扭转剪力差

如图5 所示，ts、tf、th分别为顶板、底板、腹板由于组合箱梁刚性扭转而产生的扭转剪力差。Ts、Tf、Th为顶板、底板、腹板由于组合箱梁畸变产生的畸变剪力差。 对于截取的跨中单元框架而言，剪力差为外荷载，因此框架会产生横向弯矩。 根据角点剪力流相等的原则得到：

图5 剪力差与反对称荷载

组合箱梁在偏心荷载作用时产生畸变，并产生畸变正应力。引入翘曲应力比β（β=σD/σA）,设α0=b0/b，Mu，Mb，Mc分别为顶板、底板、腹板在各自平面内的畸变内力矩，可得到下式：

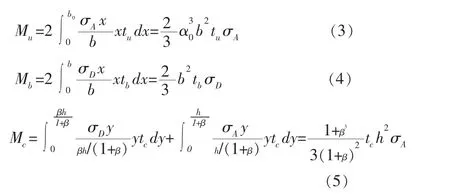
Mc对于y 轴的内力矩Mcy为：

畸变翘曲内力矩应满足自平衡关系Mu-Mb-Mcy=0，可得到关于畸变翘曲系数β 的表达式：

根据翘曲内力矩与畸变剪力差的关系得到下式与图6：

图6 各板件力矩图

2.2 框架内力及位移

由箱梁畸变理论，箱梁的畸变引起箱梁横向内力，其位移与内力的关系在畸变理论中用畸变角表示。 由于选取的单元框架来自于箱梁，因此按框架计算得到的位移与箱梁的畸变位移相协调。

由各角点弯矩平衡得到各内剪力的关系为：

式中：ηm=[3+2n＇bIc/hIu]/[3+2n＇bIc/hIb]，惯性矩Ii(i=u,b)=ti3/12(1-μ2)，钢材弹性模量与混凝土弹性模量之比n＇=Ex/Ec。 框架内剪力分析图如图7 所示。

图7 框架内剪力

在顶板作用单位水平荷载时的弯矩图与内剪力作用下的弯矩图图乘即可得到用框架内剪力表达的框架相对水平位移Δ：

图8 为框架的变形简图，在小变形情况下，框架转角γ1顶板的相对水平位移以Δ 来表示，因此γ1=Δ/h。

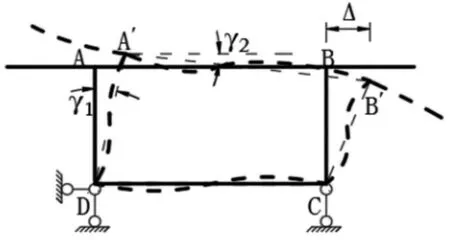
图8 框架变形简图

波形钢腹板组合箱梁横截面自身平面内服从 “拟平截面假定”，各板元内的横向挠曲满足初等梁理论，由关系式M=-EIΔ″得到各板元内畸变剪 力与位移：Δu=αTs/EcJu，Δb=αTf/EcJb, Δh=αTh/n＇EcJh。 式中系数α 与箱梁的荷载作用形式、支撑条件及计算截面的位置有关。 Ju，Jc，Jb分别为顶板、腹板、底板的纵向抗弯惯性距。

箱梁变形后（图9），箱梁顶板畸变角γ1＇，底板畸变角γ2＇,腹板畸变角γh可由各板件的相对位移表示：其中框架结构的畸变角与箱梁结构的畸变角相协调得：γ1＇+ γ2＇+2γh=2γ1。 将式（3）～（12）代入得到箱梁畸变剪力差与框架内剪力的关系：

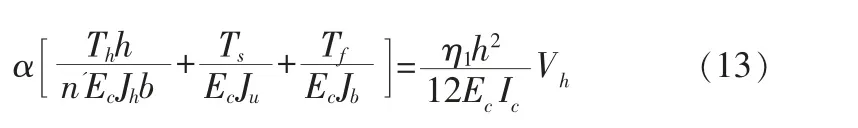
图9 箱梁畸变变形简图

2.3 有侧向水平支撑的框架内力关系

根据图4 可知，框架在顶板角点处有侧向水平约束。 根据图5、图7 作用于框架的内外力平衡，分别列出水平、竖向和下部框架绕D 点的平衡方程。

框架水平方向力平衡关系：

框架上半部水平平衡关系：

框架竖向平衡关系：

框架下半部分对D 点取矩：

通过联立式（14）～（17）得到内剪力Vs、Vf、Vh，即可得到有侧向水平支撑时组合箱梁由畸变产生的畸变弯矩。

2.4 无侧向水平支撑的框架内力关系

通过图3 可知，框架在顶板角点处没有侧向水平位移，根据内外力平衡关系得到：

波形钢腹板组合箱梁的最终横向弯矩为加支撑计算模型的横向弯矩与释放支撑时反对称荷载作用下畸变横向弯矩的叠加。

3 数值算例

以某简支波形钢腹板组合箱梁为例，计算跨径为L0=35m，b0=4.15m，b=2.075m。 顶板上距离顶板中心1m 作用偏心均布线荷载10kN/m，顶底板混凝土采用C50 等级, 混凝土的弹性模量为Ec=3.45×104MPa，泊松比为ν=0.2，混凝土顶板厚度tu=0.24m，底板厚度tb=0.22m。 波形钢腹板选择Q235，波纹型号为H1600，厚度为0.02m，弹性模量为Es=2.06×105MPa，泊松比为ν=0.3。

3.1 水平侧向支撑对组合箱梁横向内力的影响

根据公式算得有无侧向水平支撑的框架内剪力, 由求得的框架内剪力与力矩平衡关系，得到畸变效应产生的框架横向弯矩，如表1、表2 所示。

表1 释放刚性支撑后框架内剪力（单位：kN/m）

表2 释放刚性支撑后产生的横向弯矩（单位：kN·m/m）

根据弯矩分配法计算得到了图3、 图4 所示框架虚设刚性支撑时的横向弯矩。 将虚设刚性支撑得到的框架横向弯矩与释放刚性支撑后畸变产生的横向弯矩叠加，即为框架考虑畸变效应后的最终横向弯矩（表3）。

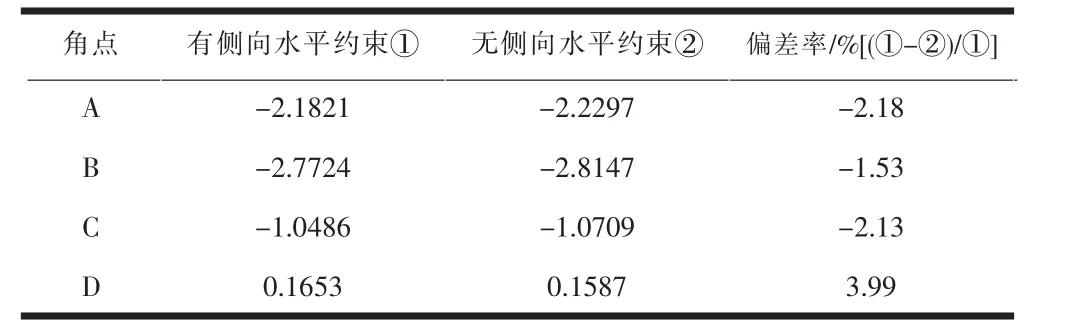
表3 箱梁最终横向弯矩（单位：kN·m/m）

从表3 可以看出，两种模型计算组合箱梁横向弯矩时的结果偏差均不超过4%，因此释放虚设侧向水平支撑对结果影响不明显，为计算组合箱梁横向内力更加简便准确，可以使用无侧向水平支撑的框架分析法计算组合箱梁考虑畸变效应影响的横向内力。

3.2 最终横向弯矩计算值与有限元对比

为验证以上理论计算方法的可靠性与准确性，利用ANSYS中SHEEL63 单元模拟混凝土顶底板和波形钢腹板。 采用四边形网格划分，共28862 个单元。 通过提取横向应力换算横向弯矩，对图3 中计算模型的横向弯矩值与有限元解进行对比，将结果列于表4 中,箱梁整体弯矩云图如图10 所示。

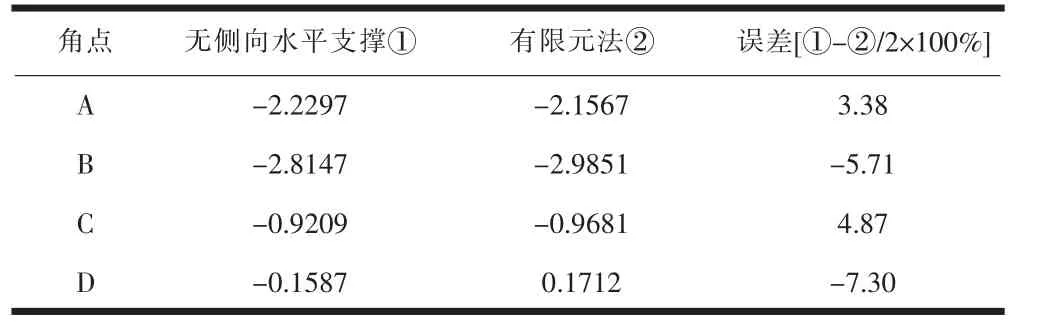
表4 箱梁横向弯矩与有限元对比（单位：kN·m/m）

图10 箱梁整体弯矩云图（N·m/m）

图3 模型考虑畸变影响的框架分析法计算波形钢腹板组合箱梁跨中截面角点的弯矩值与有限元计算结果间的偏差不大，相对误差不超过7.30%，此时可以利用无侧向水平约束的框架分析法计算组合箱梁横向内力。

4 参数分析

在图3、图4 两种计算模型下，考虑波形钢腹板组合箱梁加载点位、高宽比、顶板厚度、腹板厚度、波折角变化对顶板角点和加载点横向弯矩的影响。

4.1 加载点位变化的影响

利用控制变量法，在其他条件不变的情况下改变外荷载作用于顶板的位置，从而分析跨中截面荷载作用点位变化对组合箱梁横向内力的影响。 将左侧顶板均分为10 等份，标记顶板中点为0 点位，依次向左（图11）。

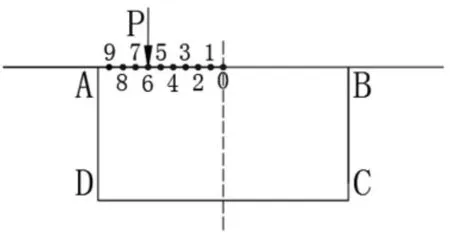
图11 加载点位

各角点和荷载作用点E 处的弯矩值均为释放虚设支撑后考虑畸变效应影响的最终横向弯矩值。 MAY为无侧向水平支撑时顶板角点A 处的横向弯矩，MAY为有侧向水平支撑时顶板角点A 处的横向弯矩值，其他点亦如此。 如图12 所示，有侧向水平支撑与无侧向水平支撑的组合箱梁各角点横向弯矩值变化趋势相同。当外荷载作用于顶板附近时，有侧向水平支撑与无侧向水平支撑计算的横向弯矩值最为接近，即偏差率最小，表明侧向水平支撑对横向弯矩影响最小。 当荷载靠近腹板作用时，有侧向水平支撑与无侧向水平支撑计算的横向弯矩值偏差变大，表明侧向水平支撑对横向弯矩影响变大，且各角点弯矩均随荷载左移而减小。

图12 加载点位变化对横向弯矩影响

4.2 高宽比变化的影响

在其他参数不变的情况下，研究高宽比变化对跨中截面顶板横向弯矩的影响，组合箱梁箱高度h 从0.415m 增加到4.15m，对应的箱室高宽比从0.1 增加到1.0（图13）。

从图13 中可以看出，当箱室高宽比增大时，顶板角点处的横向弯矩值逐渐减小，而荷载作用点E 处的弯矩值逐渐增加。 随着高宽比的增加，有侧向水平支撑与无侧向水平支撑计算的横向弯矩值偏差变大，表明侧向水平支撑对横向弯矩的影响随着高宽比的增加而变大。

图13 高宽比变化对横向弯矩影响

4.3 顶板厚度变化的影响

在其他条件不变的情况下，顶板厚度从0.1m 增加到0.35m。如图14 所示，当顶板厚度增加时，顶板角点A、B 的弯矩呈下降趋势，而荷载作用点E 处弯矩逐渐增加。 有侧向支撑模型与无侧向水平支撑的横向弯矩偏差随顶板厚度增加而减小。

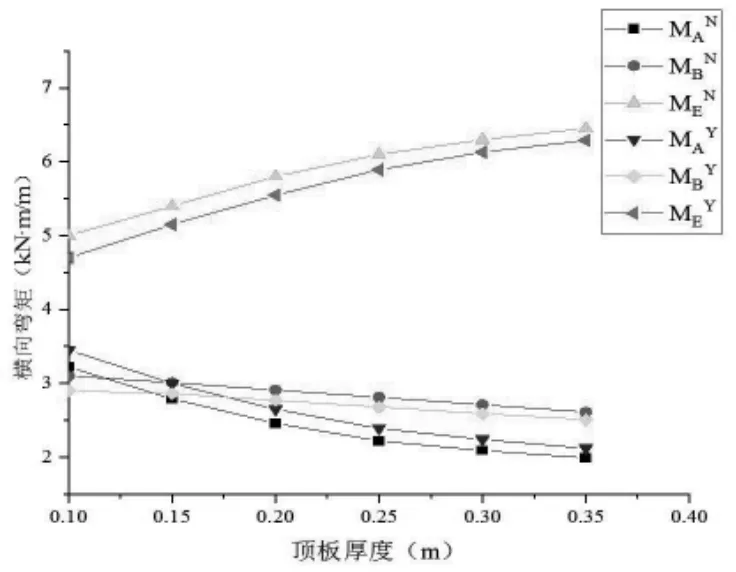
图14 顶板厚度变化对横向弯矩的影响

4.4 腹板厚度变化的影响

通过改变波形钢腹板组合箱梁腹板厚度进行分析。 波形钢腹板厚度从0.1m增加到0.35m，增量为0.05m。如图15 所示，随着波形钢腹板厚度的增加，顶板角 点A、B 处 的横向弯矩值逐渐增加，荷载作用点E 处的弯矩值逐渐减小。 有无侧向水平支撑对最终弯矩值影响较小。

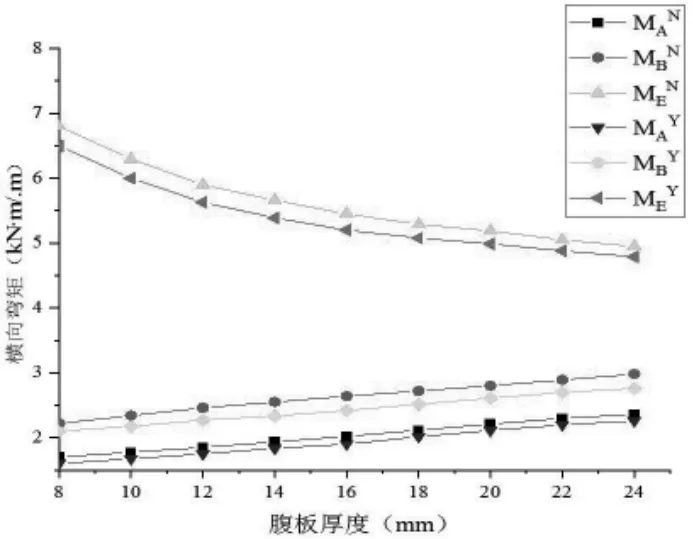
图15 腹板厚度变化对横向弯矩影响

4.5 波折角变化的影响

算例中波形钢腹板平直段长为0.37m，波折角为30.7°，在其他参数不变的情况下，波折角从30.7° 增 加 到39.7°。 如 图16所示，随着钢腹板波折角的增加，顶板角点A、B 处横向弯矩值逐渐增加，荷载作用点E 处的弯矩值逐渐减小。 有侧向支撑模型与无侧向支撑模型计算的最终弯矩值偏差较小。

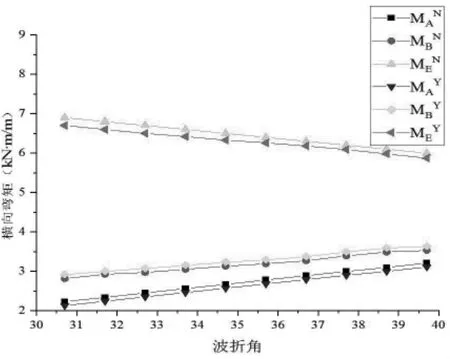
图16 腹板波折角变化对横向弯矩影响

5 结论

本文通过对波形钢腹板组合箱梁横向内力进行研究，得到以下结论;

（1） 基于框架分析法原理，给出了波形钢腹板组合箱梁无侧向水平支撑时的横向内力计算公式，并经过有限元验证，证明理论解与有限元解较为吻合；

（2） 波形钢腹板组合箱梁参数变化会影响组合箱梁顶板角点和荷载作用点的横向弯矩值。 其中，荷载点位变化、高宽比变化、顶板厚度变化时，有侧向水平支撑计算模型与无侧向水平支撑计算模型的最终弯矩值偏差较大；

（3） 腹板厚度变化和波折角变化时，有侧向水平支撑计算模型与无侧向水平支撑计算模型的最终弯矩值偏差很小，结构是否虚设水平侧向支撑对横向弯矩结果影响较小。