确定土的最大干密度和最优含水率的Cauchy 分布拟合法

许小健，涂芬芬

（1 芜湖市勘察测绘设计研究院有限责任公司，安徽芜湖 241000；2 建设综合勘察研究设计院有限公司，广东深圳 518026）

0 引言

土的最大干密度和最优含水率是工程中基槽回填、 地基处理等所涉及填土压实问题质量控制和评定的重要依据和关键参数[1]。 因此，如何通过室内土工击实试验数据快捷、方便、有效、可靠地获得最大干密度和最优含水率，是具有重要工程意义的问题。

目前，《土工试验方法标准》（GB/T 50123—2019） 和 《公路土工试验规程》（JTG 3430—2020）中均采用图解法确定最大干密度和最优含水率，即以土工击实试验数据组中的干密度和其对应的含水率分别为纵、横坐标，绘制关系曲线，再以曲线上峰值点的纵、横坐标为最大干密度ρdmax和最佳含水率ωop。众所周知，图解法的优点是可视化，可以直接观察试验数据的分布情况，因为简单易用而被工程技术人员所广泛接受，但其缺点是作图过程和利用关系曲线图读取最大干密度和最优含水率的结果会因人为因素而具有较大的任意性[2]。

当前，除图解法外，利用击实试验数据求解最大干密度和最优含水率的方法主要为数值插值法和多项式拟合法两类[3-4]。 其中数值插值法[4-8]是利用不同插值函数如Lagrange、Newton、样条曲线、分段Hermite 插值等数值分析方法处理试验成果，这类方法需要工程技术人员具备一定的数值分析理论基础；而多项式拟合法[8-14]一般以2～4 次多项式为基函数，先对试验数据进行拟合确定多项式模型的待定系数，再采用优化方法如Newton 迭代法求解高次方程极值，从而获得土的最大干密度和最优含水率。 显然，对多项式模型进行待定系数及其峰值点确定，需要进行二次求解过程，稍显繁琐，而且求解精度受计算方法影响较大。 以上方法在数据插值和拟合的实现手段上，主要采用了Matlab[11]、Spss[12]、Origin[13]、Excel[14]等商业软件等进行。

为避免人工图解法确定最大干密度和最优含水率任意性大和常规多项式拟合法二次求解繁琐的劣势，本文提出基于Cauchy 分布模型推求土的最大干密度和最优含水率的解决方案，可取得客观准确、高效便捷的效果。

1 基于Cauchy 分布的拟合模型

1.1 描述干密度与含水率关系的模型

众所周知，土的干密度随着含水量的增加而增加，当达到某一峰值后，反而会减小。这一土工击实试验数据的分布特征若用关系曲线图展现，一般呈现为上突的光滑曲线。 而拟合法作为求解土的最大干密度和最优含水率的最为常用的方法之一，Cauchy 分布密度函数性状恰好符合这一上突光滑曲线特征，因此，本文选用Cauchy 分布密度函数来进行干密度和含水率关系特征的拟合描述。

Cauchy 分布是数理统计学与概率论中常用的分布之一，在很多领域都有较为广泛的应用，其密度函数为，其中γ，μ 为参数。 当γ=1，μ=0 时，为标准Cauchy 分布。

为使Cauchy 分布能够更好地拟合土的干密度与含水率关系曲线，本文在文献[15]和文献[16]非标准双截尾Cauchy 分布密度函数的基础上引入参数ρd0，构建能更为灵活地描述含水率ω 和干密度ρd关系的数学模型，如下：

式中，ρd0，c，γ，ωop为参数。 容易发现，最优含水率ωop为参数之一，当ω=ωop时，式（1）可获得极大值，也即最大干密度ρdmax=ρd0+c/γ。

1.2 模型的求解

为确定上述数学模型，需要对其待定系数ρd0，c，γ，ωop进行求解，原理如式（2）。 对于每组试验的n（一般n=5～7）个土样的含水率和干密度击实试验数据 （ωi，ρi）（i=1,2, …,n），根据最小二乘原理，即当残差平方和达到最小值时，ρd0，c，γ，ωop即为所求待定系数值。 由于最优含水率ωop为待定系数之一，因此，最优含水率ωop在模型求解的过程中即可获得，而最大干密度ρdmax可直接由=ρd0+c/γ 确定。 由此可见，相比于多项式模型，Cauchy 分布模型无需进行二次求解就能确定最大干密度和最优含水率。

显而易见，式(2)为高次复杂非线性方程，常用的求解方法有高斯牛顿法、共轭梯度法、阻尼最小二乘法、遗传算法等。 但对于工程技术人员而言，将上述方法应用到实际问题中需要一定的数学理论知识和编程基础，具有一定的门槛，而Excel“规划求解”工具的出现极大地改变了这种情况。 Excel “规划求解”工具采用由Leon Lasdon 和Alan Waren 开发并封装后提供的“Generalized Reduced Gradient （GRG2）”代码，使得工程技术人员无需关心具体的代码，只需要简单地设定目标函数式（2）和条件，通过与Excel 界面对话交互的方式，直接调用该代码即可实现复杂问题的求解。 因使用较为简单，这里不再赘述，可通过查阅Excel 帮助文档或访问网站[17]获得相关信息。

2 应用算例

现以表1 中s1、s2 试验数据组为例来说明本文Cauchy 分布拟合法的有效性。 其中s1、s2 试验数据组分别取自《公路土工试验规程》（JTG 3430—2020）[18]和文献[8]。通过计算，Cauchy 分布拟合模型的待定系数、 拟合残差平方和SSE 的结果如表2 所示，所求可决系数R2、最大干密度和最优含水率情况见表3 和表4。 由表3、表4 可知，本文Cauchy 分布模型所得到的最大干密度和最优含水率与图解法结果较为接近；Cauchy 分布模型的可决系数R2均在0.98 以上，均优于2 次和3 次多项式拟合模型，说明Cauchy 分布模型拟合度较好。 因此，Cauchy 分布模型用于击实试验数据拟合是有效的。

表1 各数据组原始试验数据

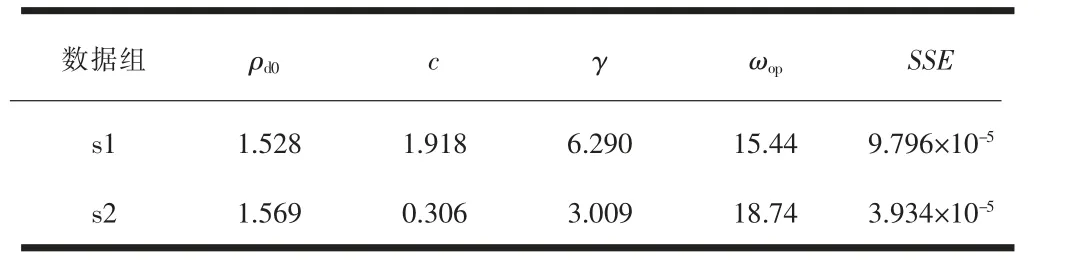
表2 各数据组的计算结果

表3 不同方法所得结果的比较（s1数据组）

表4 不同方法所得结果的比较（s2数据组）

为便于进一步观察各模型拟合击实试验数据情况，将各模型拟合s1、s2 试验数据组的结果进行可视化展示，分别如图1a)和图1b)所示。 容易发现，对于2 次和3 次多项式，其拟合结果均不如本文Cauchy 分布模型；虽然4 次多项式拟合所得可决系数R2较高，但其所拟合的曲线在两侧尾部均出现了“摆动”的情况，不符合数据发展规律，而本文Cauchy 分布模型为单峰函数，不会出现多项式“摆动”现象。可见，Cauchy 分布模型是具有一定优势的。此外，在求得最大干密度和最优含水率的效率和便捷度方面，采用多项式拟合模型，首先需要先进行多项式模型待定系数的确定，之后还需利用优化方法对已确定的多项式模型进行最优含水率极值求解，二次求解过程显得较为繁琐。 而本文Cauchy 分布模型在确定模型待定系数的过程中已将最优含水率作为参数之一进行了直接确定，使得求解过程更加高效、便捷。

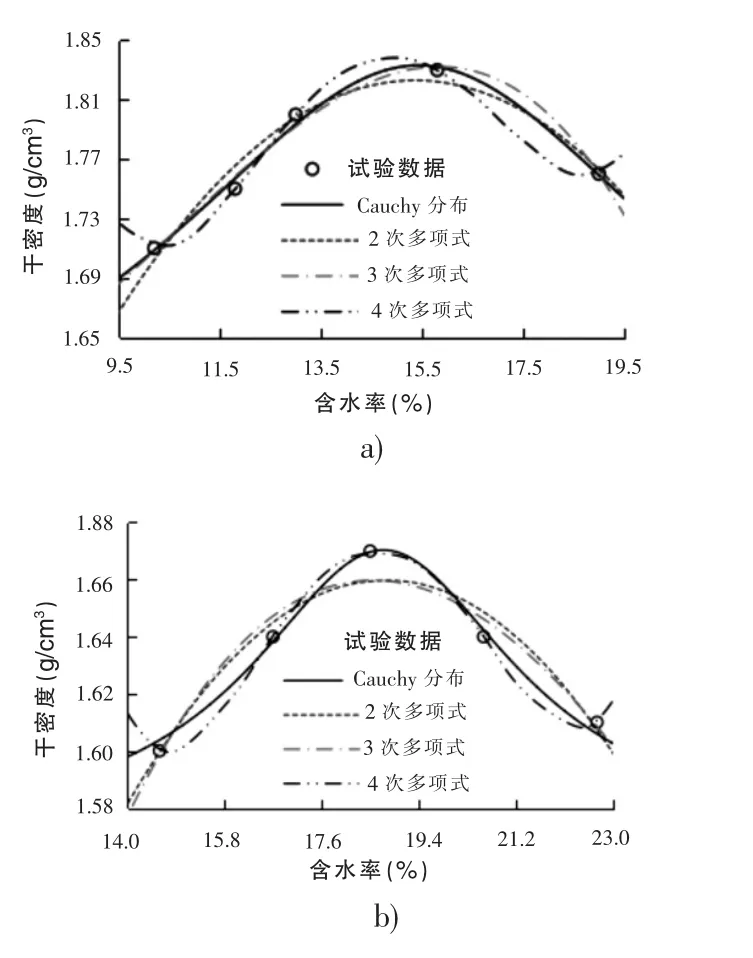
图1 各模型拟合结果的比较

3 结论

本文提出了基于Cauchy 分布拟合土的最大干密度和最优含水率的方法，对试验数据进行的应用探讨验证了Cauchy 分布拟合模型的可行性。 Cauchy 分布拟合模型避免了图解法的繁琐和具有主观性的缺陷，使得结果更为客观可靠。同时，相较于常用的多项式拟合模型，Cauchy 分布拟合模型可一次性获得最大干密度和最优含水率，使得求解过程更为高效、便捷。