翼板横向位移对箱梁剪力滞效应的影响
张玉元 张元海 张 慧
(兰州交通大学土木工程学院, 兰州 730070)
薄壁箱梁广泛应用于现代桥梁工程建设中.国内外学者就箱梁空间力学行为已开展了比较深入的研究,剪力滞效应就是其中之一.箱梁剪力滞效应是由于翼板面内剪切变形使远离腹板处的纵向位移滞后于靠近腹板处纵向位移的一种力学现象[1-5].
近年来,学者们对箱梁剪力滞效应已开展了大量的研究工作.Reissner[3]首次运用能量法建立了箱梁剪力滞效应的变分解.吴幼明等[6]运用能量法建立了3个不同广义位移的箱梁剪力滞效应解析解;与截面选取单个广义位移相比,该方法显著提高了剪力滞效应的求解精度.张元海等[7-10]运用能量变分法建立了以附加挠度为广义位移的箱梁剪力滞效应解析解;该广义位移较最大剪切转角差有明确物理意义,且便于工程人员理解和应用.舒小娟等[11]将腹板剪切变形纳入箱梁纵向位移中,建立了统筹考虑剪切和剪力滞效应的箱梁变分解,从而简化了该问题的求解过程.此外,李夏元等[12]运用能量法建立了基于修正翘曲位移模式的箱梁剪力滞效应解析解;时元绪等[13]从理论上给出了翘曲位移函数的合理组合形式;肖军等[14]分析了各种翘曲位移函数对箱梁剪力滞效应的影响;甘亚南等[15]利用变分解探讨了腹板褶皱效应对工字形梁翼板正应力的影响;周茂定等[16]建立了考虑翼板剪切效应的箱梁挠度简便计算方法.
综上所述,既有文献在建立箱梁剪力滞效应变分解时,忽略了翼板横向位移的影响(认为该项位移很小),但该位移的变化率未必很小,其对翘曲剪切应变能的准确表达具有重要影响.为了揭示翼板横向位移对箱梁剪力滞效应的影响,本文提出了一种考虑翼板横向位移影响的箱梁剪力滞效应解析方法,并分析其对剪力滞效应的影响规律.
1 翘曲纵向位移与正应力
图1为任意竖向对称荷载q(z)作用下箱梁发生挠曲变形的截面简图,将其变形状态分解为初等梁弯曲变形状态和剪力滞翘曲变形状态[7-10].
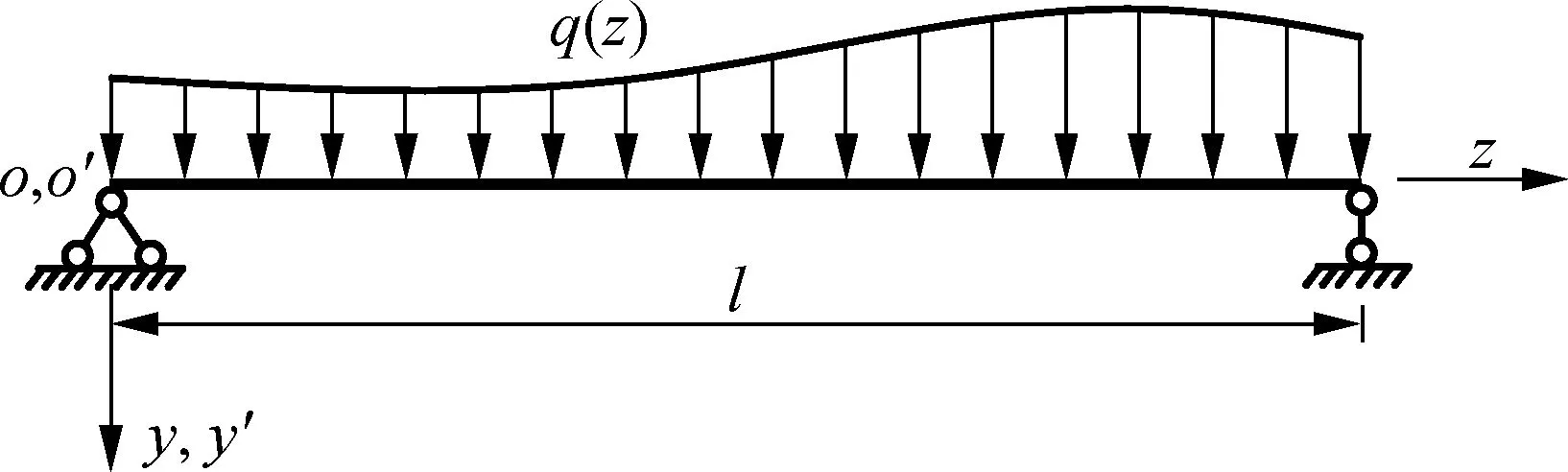
(a)坐标系及荷载

将剪力滞翘曲变形状态作为一种独立的受力状态进行分析,选取剪力滞效应引起的附加挠度为广义位移,其翘曲纵向位移uω(x,y,z)表达为
(1)

由胡克定律及几何方程可知,箱梁横截面任一点的翘曲正应力σω(x,y,z)表达为
(2)
式中,E为弹性模量.
(3)
(4)

与翘曲正应力σω(x,y,z)对应的广义力矩Mω定义为
(5)

根据翘曲正应力表达式,可导出箱梁截面任一点的剪力滞系数λ的表达式,即
(6)

2 翘曲横向位移与剪应力
图2为任意闭口薄壁杆件弯曲变形时的横截面简图,nsz为杆件中面的流动坐标系,n、s和z构成右手坐标系;uω(s,z)和vω(s,z)为翘曲纵向位移和切向位移,ψ为位移夹角.当薄壁杆件发生剪力滞附加挠曲位移f时,其切向位移vω表达为

图2 闭口薄壁杆件弯曲变形时的横截面简图
(7)
(8)
式中,γω为剪力滞翘曲剪应变.
将式(8)积分1圈可得剪应变与附加挠曲转角的关系式为
∮γωds=f′∮dy
(9)
显然∮dy=0,则∮γωds=0.沿用翘曲纵向位移模式定义方法,其翘曲切向位移定义为vω(s,z)=φ(s)ζ(z),其中φ(s)和ζ(z)分别为描述翘曲切向位移模式的分布函数和广义位移.将翘曲纵向位移uω和切向位移vω代入∮γωds=0得
(10)
ζ(z)=C1f+C2
(11)

将式(11)代入翘曲切向位移模式,可得直角坐标系下截面任一点的切向位移vω(x,y,z)表达式为
vω(x,y,z)=φ(x,y)f(z)
(12)
式中,φ(x,y)为翼板横向位移分布函数.
结合胡克定律及几何方程可得箱梁横截面任一点的翘曲剪应力τω(x,y,z)为
(13)
式中,G为剪切弹性模量.
运用有限元软件计算绘制翼板横向位移分布图(见图3),绘制时引入以下2个基本假设:箱梁顶、底板中点处的横向位移为0;变形前后翼板与腹板的夹角不发生改变.位移方向规定为:与坐标轴正方向一致为正,相反为负[18].

图3 箱梁翼板横向位移分布图
根据图3,可给出横向位移分布函数φ(x,y)的表达式为
(14)
式中,α1、α2、α3为翼板横向位移修正系数.
(15)
式中,μ为材料泊松比.
将顶板翘曲分布函数代入式(15),令x=b1,即可求得顶板横向位移修正系数α1的表达式为
(16)
同理可得,箱梁底板、悬臂板的横向位移修正系数α2、α3的表达式为
(17)
(18)
从式(16)~(18)可以看出,横向位移修正系数与泊松比、翼板宽度和跨度有关.
3 控制微分方程的建立
结合弹性理论,箱梁剪力滞翘曲变形的体系总势能Π可表达为
(19)

由最小势能驻值原理可知,对式(19)求一阶变分,并令δΠ=0,可得关于附加挠度的控制微分方程为
(20)
式中,k为考虑翼板横向位移的Reissner参数,即
分析总势能一阶变分的边界项,可以得到关于广义剪力Qω的表达式为
Qω=-EIωf‴+GAωf′=-EIω(f‴-k2f′)
(21)
常系数非齐次线性微分方程式(20)的通解为
f=C1+C2z+C3sinh(kz)+C4cosh(kz)+f*(22)
式中,C1~C4为待定系数,由具体边界条件确定;f*为仅与q(z)分布荷载有关的特解.
确定上述4个常数所需的边界条件为
固定端
f=0,f′=0
简支端
f=0,f″=0
自由端
f″=0,f‴-k2f′=0
4 箱梁剪力滞效应计算
4.1 简支箱梁
如图4所示,简支箱梁受集中荷载P作用,a、b为集中荷载作用点至左、右支点的距离.作用点左、右梁段内的剪力滞附加挠度、剪力滞系数用下标1、2表示.

图4 简支箱梁受集中荷载作用简图
根据式(22),再结合4个梁端边界条件和4个连续性条件[18],即可得到集中荷载作用下简支箱梁的剪力滞附加挠度计算公式为
(23)
将初等梁和翘曲正应力表达式代入式(6),可得截面上任一点的剪力滞系数λ(x,y,z)表达式为
(24)
4.2 连续箱梁
图5为两跨连续箱梁受均布荷载作用的示意图.为便于分析,可取其中一跨建立剪力滞效应解析解,取左跨为研究对象.

(a)两跨连续梁
根据式(22),再结合4个梁端边界约束条件[18],即可求得两跨连续梁单跨梁的剪力滞附加挠度计算公式为
(25)
将初等梁和翘曲正应力表达式代入式(6),可得两跨连续箱梁单跨梁截面上任一点的剪力滞系数λ(x,y,z)表达式为

(26)
5 算例分析
5.1 简支箱梁
以文献[18]中介绍的有机玻璃简支箱梁模型为例,如图6所示,跨度为0.8 m,跨中截面作用集中荷载P=272.2 N,材料弹性模量E=3 GPa,μ=0.385.

图6 箱梁横截面尺寸及计算点位置(单位:mm)
运用本文方法计算跨中截面各计算点的纵向应力,与文献[18]中的有限元解一并列于表1中.计算绘制跨中截面上翼板剪力滞系数横向分布图、关键点(截面)的剪力滞系数及附加挠度纵向分布图,如图7~图9所示.
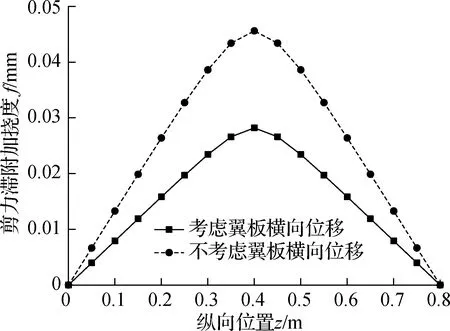
图9 简支箱梁剪力滞附加挠度纵向分布图
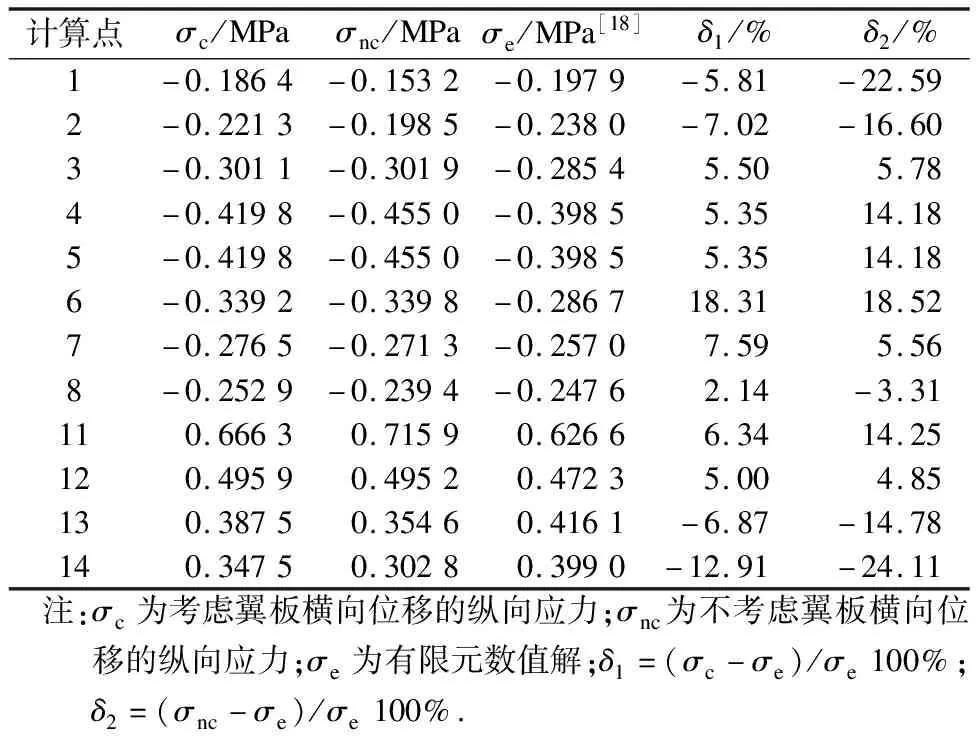
表1 简支箱梁跨中截面纵向应力对比
由表1可知:考虑翼板横向位移的计算结果与有限元数值解吻合更好,进而验证了本文方法的正确性;以有限元数值解为参照,与不考虑横向位移的计算结果相比,考虑后跨中截面顶(底)板肋处的纵向应力计算精度提高了8.83%和7.92%,悬臂板端部纵向应力计算精度提高了16.78%.
由图7可知:翼板横向位移对简支箱梁剪力滞系数横向分布的影响较小;与不考虑横向位移的计算结果相比,考虑后简支箱梁跨中截面顶板肋处剪力滞系数减小了7.88%,顶板中点处的剪力滞系数增大了4.66%,悬臂板端部的剪力滞系数增大了14.93%.

图7 简支箱梁跨中截面上翼板剪力滞系数横向分布图
由图8可知:考虑翼板横向位移时简支箱梁顶板肋处的剪力滞系数小于不考虑时的计算结果,考虑后剪力滞系数纵向分布曲线更贴近于λ=1的水平线;考虑和不考虑横向位移的剪力滞系数的差值由两侧支点向跨中截面递增.

图8 简支箱梁截面顶板肋处剪力滞系数纵向分布图
由图9可知:翼板横向位移对简支箱梁剪力滞附加挠度的影响较大;考虑翼板横向位移的附加挠度小于不考虑时的计算结果;考虑和不考虑横向位移的附加挠度差值比,由两侧支点向跨中截面递增;与不考虑横向位移的计算结果相比,考虑后简支箱梁跨中截面附加挠度减小了61.81%.
5.2 连续箱梁
以文献[18]中介绍的两跨等截面有机玻璃连续箱梁为例,其荷载示意图如图5所示,横截面尺寸如图10所示,均布荷载q=0.2 kN/m,单跨长l=0.8 m,材料参数为E=2.8 GPa,μ=0.37.

图10 连续箱梁横截面尺寸(单位:mm)
建立单跨梁ANSYS有限元模型(共划分为5 010个节点,4 992个单元),并计算跨中截面上翼板的剪力滞系数.按照本文方法计算绘制连续箱梁单跨梁跨中截面上翼板剪力滞系数横向分布图、关键点(截面)的剪力滞系数及附加挠度纵向分布图,如图11~图13所示.

图11 连续梁单跨梁跨中截面上翼板剪力滞系数横向分布图

图12 连续梁单跨梁截面顶板肋处剪力滞系数纵向分布图

图13 连续梁单跨梁剪力滞附加挠度纵向分布图
由图11可知:考虑翼板横向位移时两跨连续箱梁单跨梁跨中截面剪力滞系数与有限元数值解吻合更好,再次验证了本文方法的正确性;翼板横向位移对两跨连续梁剪力滞系数的影响较小,与不考虑翼板横向位移的计算结果相比,考虑时单跨梁跨中截面顶板肋处的剪力滞系数减小了6.81%,顶板中点处的剪力滞系数增大了2.92%,悬臂板端部剪力滞系数增大了7.42%.
由图12和图13可知:翼板横向位移对连续梁剪力滞系数纵向分布的影响较小,对附加挠度的影响较大;翼板横向位移对连续梁反弯点及中支点附近梁段的剪力滞系数影响较显著,其余梁段影响较小;翼板横向位移对剪力滞附加挠度的影响较大,与不考虑横向位移的结果相比,考虑横向位移时单跨梁跨中截面的附加挠度减小了71.08%,且二者差值比由两侧支点向跨中递增.
6 结论
1)针对箱梁剪力滞翘曲变形状态,定义了箱梁的翼板横向位移模式,解决了既有文献忽略翼板横向位移对剪力滞产生的放大效应.
2)翼板横向位移对箱梁剪力滞系数有一定的削弱作用;与不考虑翼板横向位移的计算结果相比,考虑横向位移时简支和连续箱梁跨中截面顶板肋处的剪力滞系数减小了7.88%和6.81%;考虑和不考虑横向位移的剪力滞系数差值比由支点向跨中递增,且考虑后的剪力滞系数纵向分布更贴近于λ=1的水平线.
3)翼板横向位移对箱梁剪力滞附加挠度有显著的影响;与不考虑翼板横向位移的计算结果相比,考虑后简支和连续箱梁跨中截面附加挠度减小了61.81%和71.08%;考虑和不考虑横向位移的附加挠度差值比由支点向跨中递增.

