百万扩招背景下高职数学之教学实践

王咏芳

(江苏省太仓市苏州健雄职业技术学院 215411)

李克强总理在2019年的《政府工作报告》中要求的百万扩招政策，使职业院校生源结构更加多元化，必须全面构建开放式、个性化的学习体系.数学课程在其中扮演了重要角色.数学学习的过程不仅是知识积累过程，更是恰当学习方法的探索与掌握的过程.

1 调查摸底，背景分析

经过调查问卷、座谈会和聊天交流等摸底后，发现扩招生源的结构十分复杂，可以用“大”来概括：一是年龄相差大，出现了父子同学；二是基础相差大，有简单四则运算不熟练的，也有刚学过一些微积分的；三是学习目的相差大，有刚出校门暂不准备工作的，也有在社会上“闯荡”多年急需“充电”的；四是可支配时间相差大，有可脱产的，有工作脱不开身的.

基于生源的实际情况，在数学课堂上必须破解规模化和个性化、共性需求和个性需求包容的平衡结构瓶颈，形成更加恰当的“因才施教”范例.基本思路为：首先，学习的基本路径必须是“平缓”的，必须是“深入浅出”的.其次，以“以直代曲”为切入点，引导学生去思考，去分析问题、分解问题、解决问题，在实现问题分解的同时也实现了难点和主要矛盾的转移.第三，留有“端口”，许多“支节”问题、特殊问题，不作为课堂内容，或者在课堂上提示一下，作为课后作业布置.目的是培养学生自主学习能力，寻找最佳的个性化学习方法，实现教与学的分层分类.

2 扬长避短，以人为本

2.1 拾遗补缺

目的是解决部分基础差的同学存在的“短板”，以小组、结对为主，互帮互学，老师适当补充讲解、督促、检查，已经会的同学通过互帮互学时的讲解能提高掌握程度，提高表达能力，没学过的同学能找到自己的“不足”之处.

2.2 清障梳理

以基本初等函数为载体和目标，从数的运算，到用字母代替数，再到方程、函数，最后是平面直角坐标系中的图象、性质，引领同学们发现“短板”障碍，并解决问题.初步建立数形结合的思想方法：由图象记忆性质，由性质记忆图象.

2.3 以直代曲

作为微积分学中三大计算的切入(引入)点，通过“承认误差、减小误差、消灭误差”三步骤，将问题进行边分析、边分解、边解决，形成数学中朴素的、易懂易用的思想方法：“以直代曲”.

2.3.1 数列极限的概念是以圆内接正多边形面积代替圆面积来引入，具体做法如下.

(1)在以圆内接正三角形面积S3、内接正六边形面积S6、内接正十二边形面积S12、…来代替圆面积S，用PPT动画表现出来，可以与同学们逐步达成共识：①用直线段代替了圆弧线；②内接正多边形面积是可以计算的；③形成了一个无穷数列；④每一项都与圆面积有误差；⑤项数越往后，误差越小；⑥有必要观察这个数列的变化趋势，但这是一个无法逐一去完成的任务！

(2)引入针对上述数列的描述性定义：

纯文字：当项数不断向后推进时，内接正多边形的面积越来越接近于圆面积；

半文字：当n→∞时，Sn→S；

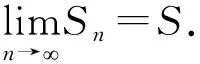
共识：数学是简洁的！内涵是丰富的！

(3)正式讲述数列极限的描述性定义，并通过几个简单的、典型的数列说明：收敛与发散，单调收敛与跳跃收敛，定向发散与不定向发散，并强调记忆.

共识：极限是变化趋势；有极限计算这类需求；极限计算是问题的核心、重点、也是难点，暂时搁置，以后专门解决.

(4)拓展端口.以问问题的形式，或自问自答，或请同学回答，也可先小组讨论选代表回答，还可以留作课后复习、作业，留作下次课前回答，可以书中找、网上搜等等.本知识点有以下问题可以提出.

①不是正多边形可以吗？

②用相同的方法求周长可以吗？

③是否可以用外切正多边形来解决问题？

④内接正边形的面积构成的数列的增减性如何？外切的呢？(注：此问题为定理“单调有界数列必收敛”作准备，也为两边夹定理作例子)

⑤比较：内接正三角形面积S3，内接正六边形面积S6，内接正十二边形面积S12，…，以及，内接正三角形面积S3，内接正四边形面积S4，内接正五边形面积S5，…，构成的两个数列的区别与联系.(子数列问题，包括增减有限项问题)

⑥对“趋向(于)”是怎样理解的？

⑦试算一下内接正n边形的面积.(为第一个重要极限作准备)

⑧数列是函数吗？有什么特殊性？

(5)本知识点的课堂用时为一个学时，用圆内接正多边形面积代替圆面积，以达到三个目的：一是“以直代曲”思想，即：“承认误差、减少误差、消灭误差”这一数学思想方法；二是无穷数列的变化趋势是有这方面的需求的；三是复杂的计算和观察变化趋势“暂时搁置”—有需求但另议，实现问题分解和矛盾转移.

2.3.2 导数的概念以自由落体运动为例引入

(1)物理学中知道：自由落体运动中，路程S是时间t的函数，并且有

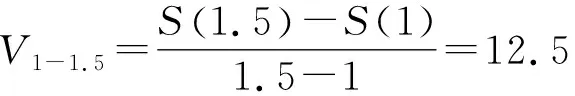
问题：1秒时的瞬时速度V(1)=？

(2)显然，我们可以用上面三个平均速度任何一个来代替—承认误差，根据生活经验与分析，时间间隔小的误差也小，于是有1秒到1+Δt秒时的平均速度：(减小误差)

Δt越小时，误差越小，所以取极限：(消灭误差)

所以有：自由落体运动中，1秒时的瞬时速度是10m/s.

共识：计算瞬时速度时需要计算路程改变量与时间改变量比值的极限，简称“差商极限”.

(3)拓展设问:①能否用0.5秒到1秒的平均速度代替1秒时的瞬时速度？试算一下;②能否用2秒到3秒的平均速度来代替?③将自由落体运动改为变速直线运动时，计算有什么区别？改成变速圆周运动呢？

(4)还可以通过切线斜率的计算，归纳出：差商极限的计算是有需求的，但具体计算是相当不容易的.导数计算就是解决主要矛盾，发扬“迎着困难上”的精神.

2.3.3 定积分的引入可以用均分求面积来引入

以标准抛物线在[0，1]区间上所围面积计算为例，等分计算长条面积并求和：近似面积(承认误差)，份数越多误差越小(减小误差)，取极限(消灭误差)；又一次展现“以直代曲”的解决方法.

2.4 问题解决.极限、导数、积分三个定义中都将矛盾进行了的转移，转移成微积分学中的三大类计算.

2.4.1 极限计算只需掌握若干个基本的未定型，包括两个重要极限，即从最简的几个极限出发，配以极限的四则运算法则，来完成极限计算.以最佳求解方法为范例，不作一题多解.

2.4.2 导数计算时，是围绕着“凑”公式进行，从直接凑公式到掰开了凑，只是利用四则运算法则时不能想“当然”：乘与除的法则是掰开了“组合”地凑！复合函数求导时，是“借用公式的凑”，将含自变量当成自变量凑用公式，后乘含自变量式的导数.

2.4.3 定积分计算最为简单，只需正确书写微积分基本公式.强调计算时细心即可.

3 融会贯通，厚积薄发

微积分学作为高职数学的一门基础课程，其作用是多方面的.

一方面是知识的积累，明确已有成果，不走“重复路”：不必去做“割圆术”，也不必去一一证明导数公式；而是要“多多益善”地知道数学已解决的、可解决的问题.

另一方面是数学的思想方法，“以直代曲”就是简单实用的一种数学的思想方法，是复杂问题分解成多个简单问题的一种处理手段.

第三方面是数学式的表达，从数学的角度来看，理解或掌握的知识点并不一定能恰当地表达出来，“恰当地表示”就是用最为简洁的、易懂的、严密的(不引起岐意的)表达出来，换言之就是，数学中的定理都是简洁而内涵丰富.例如，初等函数在其定义区间内都是连续的.不足二十字的定理，其中的内涵可以推敲多时.

由此可见，数学课程的学习，在整个学习过程中的作用是重要的，是其它课程无法替代的，更是为学生可持续发展打造出一个基础平台，一个具有相当的数学知识和数学能力的平台.为更好地建设这个平台，结合扩招生源的实际情况，设计了上述的课堂实施线路图.让学生始终明确“要做什么，怎么做”，学会分析、分解问题、解决问题的总体线路，潜移默化地让学生克服对数学的恐惧心理，养成良好的学习方法、习惯.同时，留下相当的拓展端口，鼓励学生进行查阅各种教材及上网搜索，为个性化学习提供方向.