在高中数学解题中应用转化思想的几点思考

程新益

(江苏省江阴市要塞中学 214431)

高中数学的教学重点不仅仅只是让学生掌握数学的基本知识和理论，其实践性和难度都比初中数学高得多，因此，在高中数学的教学过程中，不应只让学生通过“刷题”来提升自己的解题能力，教师应将数学思维、数学思想融入教学过程中，让学生能够捕捉到解题的方法、重点、思维，快速高效的进行解题.转化思想是数学解题思想的重要思想，其可将复杂的问题简单化，陌生问题熟悉化，有助于学生思维严谨性的提升，良好的解题习惯也会随之逐渐形成，进而能撬动学生的思维，在启智明理中促进学生自主学习，从而提高教学质效.

1 转化思想在高中数学解题中的意义

高中数学题目(尤其是理科数学)的难度和抽象性皆明显高于初中数学，学生在解题过程中，教师可以将转化思想运用于解题过程中，进而达到快速解题的目的.转化思想要求学生通过侧面或反面整理解题思路，寻找突破口，把复杂、抽象、困难的问题转变为成一个或若干个自己熟知的或能解决的问题.在学习数学的过程中，大部分学生会将一个较难的问题通过分解、变形、代换、平移、旋转、伸缩等多种方式，将之转化为一个或几个自己熟悉的基本的问题，从而求出答案.在解答一元二次方程时，学生可以将一元二次方程通过因式分解转化为一元一次方程.

2 在数学解题过程中利用转化思想的策略

2.1 将复杂问题简单化

复杂问题简单化，可以是一个数学公式，一个数学概念，一个数学定义，也可以是有关数学公式的记忆，数学定义的证明等等.下面我就如何简单数学问题说我的几点看法: 一、用自己熟悉的、精简的语言阐述数学概念和定义.这样有利于加强概念、定义的理解和记忆.比如，在我讲抛物线方程的时候，抛物线方程与焦点位置有密切关系，抛物线方程一次项即是焦点所在位置.而切抛物线的焦点与抛物线方程的系数的四分之一倍数有关.这里我用自己的语言向同学们总结.抛物线的方程要么是x2等于好多y,要么是y2等于好多x，这主要就看焦点位置了，如焦点在x轴，一次项就是x，所以方程就是y2等于好多x.以次类推.当面临一道结构复杂直接解答会难以上手的问题时，可将该问题划分为一个或多个简单的问题，逐个解答.例如以下题目：

2.2 将常量转变为自变量

变量转化多用于含有X未知数的不等式问题，在做该类题目时，需根据题目的条件求出参变量的取值范围，虽然该类题目的做题方法多，即：对其分类讨论、数形结合、分离参数、利用函数性质，但次过程较为复杂，出错了较高，若能使用变量转化则可事半功倍.例如以下例题：

例1设a,b是两个实数,A={(x,y) ∣x=n,y=na+b,n∈z},B={(x,y)∣x=m,y=3m2+15,m∈z,}C={(x,y) ∣x2+y2≤144}是否存在a,b使得(1)A∩B≠____;(2)(a,b) ∈C同时成立.

方法一假设存在(x,y)∈A∩B,则相应的直线y=ax+b与抛物线y=3x2+15有公共点.

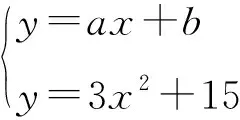
△=a2-12(5-b) ≥0，即-a2≤12b-180，

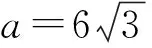
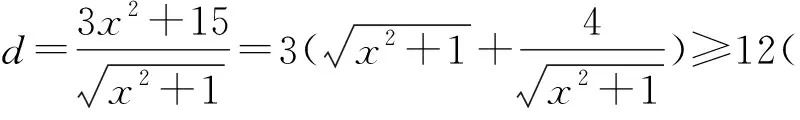
所以a,b不存在.

分析以该题为例，解法一采用X为变量，带入过程较为复杂，计算量大，学生在解题的过程中，容易出现作物；而解法二是将a、b等转变为变量，将X作为常量，转化思维，解题过程简单易懂，由此看出解决此题选a,b为变量,x为常量同样是可以找到一种优质的解法.如何设定主元，对学生的思维能力的要求较高，主元选定之后，有助于用方程或函数思想来解决问题.

2.3 将抽象问题形象化

学生在解答抽象问题时，往往会出现找不到解题思路的情况，尤其是函数问题，此时便可采取抽象问题形象化的解题方法解决，将抽象问题形象化主要有换元法、凑合法、待定系数法、利用函数性质法等.

2.3.1 换元法

即用中间变量表示原自变量x的代数式，从而求出f(x)，这也是证某些公式或等式常用的方法，此法解培养学生的灵活性及变形能力.

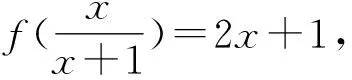
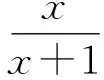
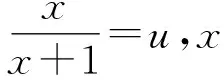
2.3.2 凑合法

该方法是在已知f(g(x))=h(x)的条件下，把h(x)并凑成以g(u)表示的代数式，再利用代换即可求f(x).此解法简洁，还能进一步复习代换法.

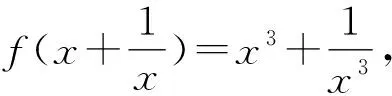
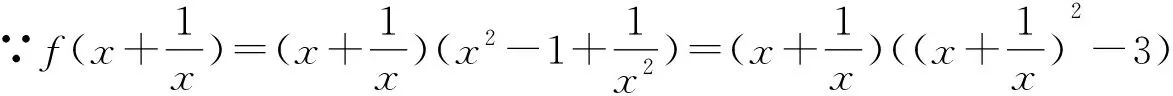
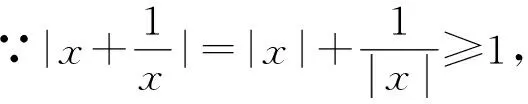
∴f(x)=x(x2-3)=x3-3x，(|x|≥1)

2.3.3 待定系数法

先确定函数类型，设定函数关系式，再由已知条件，定出关系式中的未知系数.

例4已知f(x)二次实函数，且f(x+1)+f(x-1)=x2+2x+4,求f(x).

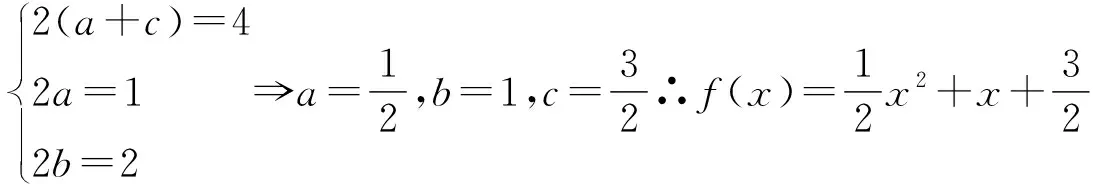
2.3.4 利用函数性质法

主要利用函数的奇偶性,求分段函数的解析式.

例题已知y=f(x)为奇函数,当x>0时,f(x)=lg(x+1),求f(x).

解析∵f(x)为奇函数，

∴f(x)的定义域关于原点对称，故先求x<0时的表达式.

∵-x>0,

∴f(-x)=lg(-x+1)=lg(1-x),

∵f(x)为奇函数，∴lg(1-x)=f(-x)=-f(x)

∴当x<0时f(x)=-lg(1-x)

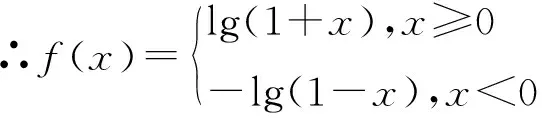
2.4 静态问题动态化

部分数学问题在以静态的思路进行解题可得出结果，但过程复杂，学生在做题过程中容易出错，因此，在做该类题目时，可将静态问题动态化，即：通过研究变动情况对题目可能出现的特殊情况进行分析，进而简化解题过程，防止错误的发生.

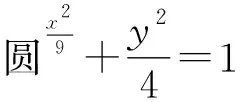
解题过程解 ①若∠PF2F1=90°.

则|PF1|2=|PF2|2+|F1F2|2，

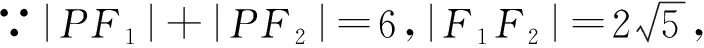
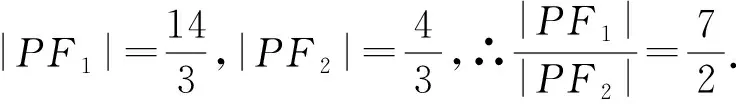
②若∠F1PF2=90°，则|F1F2|2=|PF1|2+|PF2|2，

∴|PF1|2+(6-|PF1|)2=20，

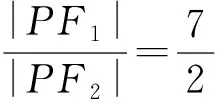
分析改题目的直角位置为得到确定，因此，在解题过程中，我们需要先确定直角可以确定的位置，在以分类的方式对直角的位置进行确定，最后对所有可能出现的可能进行汇总，进而得出范围.解答问题则可要让，F1和F2动起来，对其进行分类讨论，以提高解题的效率.

转化思想是数学解题思想中的重要部分，其可将复杂的问题转化为简单问题，抽象问题转化为具象问题等，可帮助学生提升解题效率，降低错误率的发生，对于学生提高成绩具有重要意义.其次，转化思想可有效锻炼学生的思维逻辑能力，提升其做题的严谨性，进而使其做事的思维能力、严谨性得以有效提升，为其未来的发展奠定坚实基础.因此，高中数学教师在教学过程中，应将该思想广泛运用，帮助学生领悟解题方法，掌握解题能力，为其高考提供坚实保障.