高中数学核心素养的培养之数学运算能力

李海龙

(甘肃省庆阳市华池县第一中学 745600)

无论是从应试还是发展数学能力的角度来看，培养学生的运算能力都有着重要的意义.教师应当对现有教学模式作出调整，将数学运算训练纳入日常教学当中，让学生有更多解决数学问题、锻炼运算能力的机会.在教学安排得到优化的情况下，学生也会逐步形成良好的学习习惯，更加主动地开展运算练习，从而在运算中积累经验，深化对数学知识理论的了解，快速提升数学运算能力.

1 高中学生数学运算水平低的主要原因

数学运算能力作为数学六大核心素养之一，其培养工作已经受到教学工作者们的广泛关注.结合教学实际可以认识到，当前有不少高中学生在解决数学题目时呈现出低水平的运算能力，而这也使得学生数学成绩不理想，对数学学习逐渐丧失信心.究其原因，可以认识到这种状况的产生主要可以归咎于以下几点，高中数学教师有必要对这些因素进行了解，然后再提出相应的训练措施.

1.1 审题不清

高中阶段的数学运算题中有不少需要事先审题，学生们在运算以前需要对图形、文字作出分析，然后才能用已知的信息进行运算.但恰恰有很多学生在这项过程中就会出现问题，一些学生为了节约做题时间，一拿到题目就对已经知道的信息进行运算，全然不顾数字间的关系，这样不仅不能节约时间，还会导致运算方向错误.还有，正确运算的前提是正确使用数据和公式，但是一些学生的解题过程中容易急躁，或者是在解题思路上产生偏差，这就使得学生会将错误的数字和公式应用于解题环节.如此一来，解题的结果也就可想而知.

1.2 数字计算错误多

数字计算错误多是运算能力提升道路上的一块绊脚石，数学是一门严谨的学科，在计算方面尤为如此，任何细微的误差都会导致最终的错误.学生解题正确性不高有很大程度是因为计算过程不严谨，错误多，这种状况的出现与学生的学习习惯有很大的关联，如马虎、不认真的学习态度，运算时比较随意，没有做到有序书写；运算结束以后不加验算，这些问题都会影响数学运算的正确率.我们都知道，保障解题的正确性主要从思路分析和实际计算两点入手.但是在实际解题时，有些学生花费精力理清了数学思路，但是在计算时却没有考虑好合理性、简洁性，想到什么就直接写到草稿纸上，所以草稿纸上的计算过程杂乱无章，提取有效计算结果的时候也很容易受到干扰，即使得出了正确的计算结果也会在整理中消耗精力和时间，进而在复杂的计算中受到干扰，这样也会在一定程度上妨碍正确答案的获取.

1.3 解题过程混乱

解题方向正确是有序解题的前提条件，很多数学题目解答以前都要求学生分析题目，然后再确定解题方向.若是学生在运算一开始就找错了方向，那么解题失误也就无可避免，数学成绩的提升更是无从谈起；在解题过程中，部分学生会出现思维意识欠缺的问题，具体表现为逻辑思维能力差，题型变化以后就显得一头雾水；最后就是对解题的过程没有反思，“学而不思则罔”这句话在数学中同样有效，而且数学知识体系严密，如果学生不能经常对自己的解题思路进行反思，就无法稳固数学基础知识，这样就会导致运算能力的发展事倍功半.

1.4 课堂学习效率低下

数学运算本身是对各项数学知识、公式的应用，所以提升数学运算能力的前提就是牢固掌握知识.结合教学实际来看，数学运算能力不佳的学生普遍存在知识掌握不牢、理解不到位的状况.具体分析以后，可以将问题的症结归咎于课堂学习效率低下，高中阶段的教学任务紧张、节奏快，教师在课堂教学中往往会抛出大量的知识点，对于具体的运算和解题思路则是一笔带过.除此以外，数学教师和学生的交互也相对较少，教师虽然会对练习中的错题进行讲解，但却无法了解到学生出现运算错误的原因，所以学生运算能力的提升比较缓慢.

2 高中核心素养理念下学生运算能力培养方式

2.1 帮助学生养成良好的运算习惯

保持良好的运算习惯有利于提审审题正确性，帮助学生稳定持续地提升运算能力.上文中已经提到审题不清是学生运算水平低的重要原因，教师在运算教学中应当规范学生的审题行为.部分学生为了提升解题效率，在做题时比较心急，经常只凭经验判断解题思路，然后再将关键数值纳入公式中进行运算.这种行为虽然有时可以为学生带来便利，但是审题不清带来的失误风险也同样不可忽视.为此，教师在运算训练中要教会学生审题，在仔细斟酌文字后将题目中出现的数字关系列出，然后再思考题目的最优解.在解题时应当尽量保证书写规范、计算流程整洁，这样才能为后续的验算提供便利.除此以外，教师要培养学生养成自主训练学习的好习惯，毕竟教师的时间、精力有限，想要兼顾到每个学生的运算训练几乎不可能实现.不过这并不意味着教师作用的缺失，教师要结合学生的信息反馈做出适当引导.例如在自主训练刚开始时，教师可以专门用一堂课开展运算活动，让学生明白教师对运算的重视，并对学生进行自主训练方法教导.

2.2 引导学生持续学习

数学运算能力的提升并非一蹴而就的过程，高中数学教师在培养学生运算能力时不能操之过急，而是要做好长期教学的准备，尽可能的引导学生走上学习的正途.因此，教师要从以下几点入手，首先是强化课堂教学效果，高中数学知识囊括概念、公式等多种形式，学生们在运算时经常要用到多重公式，如三角函数、双曲线定义等，为了让学生在解题时从容进行运算，就必须给出针对性、目的性的练习，帮助学生掌握和巩固各类知识；其次，数学运算能力的提升需要持之以恒的努力，不少学生学不好数学就是因为害怕犯错，逐渐失去对数学的信心.

2.3 注重基础训练

数学运算的过程中，学生需要对运算对象、运算方向、运算法则和计算结果等环节合理兼顾.为了让学生的数学运算能力有序的发展，教师还是要从基础训练的角度入手，让学生对基础运算法则形成基本认识以后再做题积累经验.所以说，教师在培养学生数学运算能力时，应当有意识地增加知识训练内容，引导学生将题目对应的公式、概念应用到运算中，促使学生将所学知识应用于解题当中.

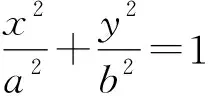
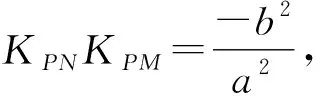
3 结合学生需求展开运算训练

核心素养的培养以学生为出发点和落脚点，在实施教学时必然要将学生当作主体，即使是运算训练中也要如此.教师在训练活动中要时刻关注学生的反馈意见，根据学生的发展需求和建议调整训练活动.尤其需要注意的是，不同的学生在做题时选择的方式各不相同，教师可以以此为契机培养学生的一题多解思维.实际上，一题多解可以在很大程度上体现出学生的运算能力，在课堂上可以适当留出时间让学生参与不同解题的研讨，经过思考和讨论以后，学生对数学知识的认知会变得更加深刻.

例2求经过两条直线x+2y-1=0 和2x-y-7=0 的交点，且垂直于直线x+3y-5=0的直线方程.

4 优化运算策略，明确运算方向

运算策略是学生经过长时间练习的经验总结，从某种角度来说就是“解题套路”.学生使用方法总结快速解题是运算能力发展的必然结果，当然教师要指导学生有选择地使用套路解题，而不是在固定思维的桎梏下限制自身核心素养的长期发展.在高中数学分类讨论问题中，学生经常会因为运算方向不清晰花费大量时间解题，有时甚至付出了时间和精力也不能得到正确的答案.为了在考试中取得优势，学生要缩短思考时间，尽量避开不必要的思考，以免思维混乱、运算方向被干扰.

例3不等式x2-4x+p+x-3≤5，当x最大值为3时，p的值为多少？

解析解决此类题型时，学生看到题目的第一个念头就是将绝对值代入不等式，然后再对p值的存在情况作讨论.但是从题目可以看出来绝对值的存在造成了不小的干扰，若是坚持使用代入讨论的方法，学生就会花费很多的时间，在考试时间有限的情况下，这种方法明显不合适.转而应当从最大值是函数的端点值出发，再借助不等式的性质将参数具体化，将端点代入后，得出8和-2两个值，又p=-2时不满足题意，所以p=8.

在高中数学中培养学生运算能力的重要性不言而喻，教师必须在充分认识到运算能力对提升学生数学成绩、培养学生数学核心素养积极作用，用合理的教学手段在日常教学活动中强化运算能力培养，有效提高学生运算正确率，让学生在取得良好成绩的同时重拾学习数学的信心.