一个基于群作用的有趣例子
霍丽君, 程卫东
(1.重庆理工大学理学院,重庆400054; 2. 重庆邮电大学理学院,重庆400065)
1 引 言
群作用[1-3]是抽象代数或者群论课程中的重要概念,群论的很多结论或应用都是从这里起步,比如,在证明Sylow定理和Burnside定理的过程中,群作用的思想就起了关键性的作用.实际上,对各种群作用进行考察是现代数学研究的重要手段;同时,群作用还广泛应用于诸如物理、化学、力学等不同的科学领域.
群作用的概念对初学者往往较为抽象,教师在讲授过程中采用一些较为具体的实例进行讲解是非常有必要的[4],最好能选取学生较为熟悉且具有几何直观的例子.矩阵的合同关系是学生在线性代数课程中学习过的基本概念,本文运用群作用的思想重新考察二阶实对称矩阵的合同关系[5-6],通过分析群作用的轨道在三维欧氏空间3中的图像,可以发现这些图像由某些二次曲面[7-8]张成.同时,根据群作用的轨道划分理论[1]还可说明这些二次曲面恰好可以将三维欧氏空间填满.本文给出了一个具有强烈几何直观的群作用的例子,这个例子对激发学生学习抽象代数的兴趣以及理解群作用思想的实质均会产生积极影响.
回顾群在集合上作用的定义[1]:
设G是一个群,e是G的单位元,X是一个非空集合.如果给了一个映射f∶G×X→X, 且对所有的g1,g2∈G,x∈X, 满足:
(i)f(e,x)=x;
(ii)f(g1g2,x)=f(g1,f(g2,x)),
就称f决定了群G在集合X上的一个作用.
2 一个例子:一般线性群在二阶实对称矩阵集合上的作用
考虑由所有二阶实对称矩阵构成的集合X,根据线性代数理论,对任何A,B∈X,如果存在非奇异实矩阵P,使得PAPT=B,那么就称B与A合同(或相合).由实对称矩阵的惯性定理[5],任取二阶实对称矩阵必与且仅与下面6个矩阵中的一个合同:
设GL2()是实数域上的一般线性群,即全体二阶非奇异实矩阵构成的乘法群.GL2()中任一元素P都可以定义集合X到其自身的一个映射:
σP∶X→X,APAPT, ∀A∈X.
(1)
容易验证该映射给出了群GL2()在集合X上的一个作用.实际上,只需在前述群作用的定义中取映射f:GL2()×X→X, (P,A)PAPT即可.进而在集合X上定义一等价关系“~”:称矩阵A和B等价,如果存在映射σP使得σP(A)=B,即A与B合同.在这一等价关系下,集合X被划分成6个等价类,每个等价类称为由(1)式定义的群作用的一个轨道.于是X被划分成了如下6个轨道
Oi={PFiPT|P∈GL2()},i=1,2,…,6
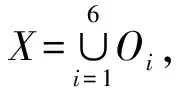
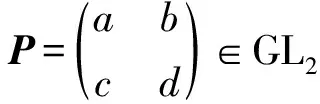
其中O6是由2阶零矩阵单独构成的一个轨道.
进一步地,在全体二阶实对称矩阵集合X与三维欧氏空间3之间建立映射:

(2)
不难验证τ是X与3之间的一一对应.在该映射之下,群GL2()作用在X上生成的6个轨道在3中的像分别为
经过计算可发现O′1和O′2中的点满足方程
xy-z2=(ad-bc)2=t2,
(3)
其中t=ad-bc≠0.
O′3中的点满足方程
z2-xy=(ad-bc)2=t2,
(4)
其中t=ad-bc≠0.
O′4和O′5中的点满足方程
xy-z2=0.
(5)
显然O′6中的点亦满足方程(5).
这就说明,全体二阶实对称矩阵在上述群作用下的6个轨道在三维欧氏空间中图像(通过一一对应τ)总落在由方程(3)-(5)所定义的二次曲面上.实际上,因为映射τ是一一对应,对任意一点P∈3,总存在实数t,使得P满足方程(3)-(5)中的某一个.
为了更加直观地看出方程(3)-(5)所表示的几何图形,做可逆变量替换[7-8]

代入将(3)-(5)分别化为
u2-v2-w2=t2,t≠0,
(6)
-u2+v2+u2=t2,t≠0,
(7)
u2-v2-w2=0.
(8)
从(6)-(8)立即看出,O′1和O′2由三维欧氏空间3中的一族共轴共中心的双叶双曲面构成,这些双叶双曲面的方程由(3)(在(u,v,w)坐标系下由(6))给出,其中O′1对应于u>0的一叶,而O′2对应于u<0的一叶.O′3由3中的一族共轴共中心的单叶双曲面构成,这些单叶双曲面的方程由(4)(在(u,v,w)坐标系下由(7))给出.O′4和O′5由3中的一个圆锥面去掉原点后构成,其方程由(5)(在(u,v,w)坐标系下由(8))给出,其中O′4对应于u>0的一支,而O′5对应于u<0的一支.最后,单点集O′6对应于3的坐标原点.
实际上,当非奇异矩阵P在群GL2()中变动时,方程(3)和(4)(或者(6)和(7))中的参数t取遍全体非零实数,这是因为对任意非零实数r,总存在二阶可逆方阵()满足其行列式等于r.当这个参数t趋于0时,它们对应的二次曲面分别趋于(5)(或者(8))所表示的圆锥面;而当参数t趋于无穷时,它们对应的二次曲面分别逐渐远离(5)(或者(8))表示的圆锥面.实际上,(5)(或者(8))表示的圆锥面分别是(3)和(4)(或者(6)和(7))表示的双曲面的渐近锥面.
特别地,在(u,v,w)坐标系下,取定某个t后,(6)-(8)表示的三类二次曲面之间的空间位置关系如图1所示(注:图1由Wolfram Mathematica®9软件绘制).

图1 双叶双曲面、圆锥面和 单叶双曲面关系示意图
3 结 论
本文考察了一般线性群GL2()在全体二阶实对称矩阵所构成的集合X上的作用,给出该作用下的轨道在三维欧氏空间3中的几何图像(通过映射τ),说明这些轨道分别由双叶双曲面、单叶双曲面以及圆锥面这三类二次曲面张成.同时,结合二次曲面方程的连续演化以及群作用的轨道划分理论[1],说明这三类二次曲面填满整个3.
本文将有助于对群作用这一基本概念产生直观感性认识,同时也能使学生加深对矩阵合同、二次曲面等知识点的理解,本文对线性代数和抽象代数等课程的教与学具有一定的启发意义.
致谢作者非常感谢文献[3]对本文的启发以及审稿专家提出的宝贵意见.

