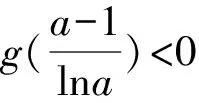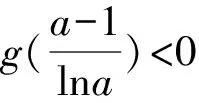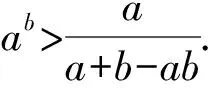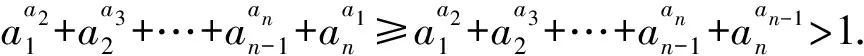一个精彩不等式的探究和推广

邓启龙

(广东省中山纪念中学 528454)

有一个非常精彩的不等式：a,b∈(0,1),ab+ba>1，该不等式结构巧妙，形式优美．本文首先给出该不等式的两种证明方法，然后将该不等式推广到多元形式．

为了行文方便，将变量b改为变量x，构造函数f(x)=xa+ax，通过求导来探究函数f(x)的单调性，从而证明x∈(0,1),f(x)>1，于是得到证法1．

证法1令f(x)=xa+ax,且x∈(0,1),a∈(0,1)，则

f′(x)=axa-1+axlna

g′(x)=(a-1)xa-2a1-x-xa-1a1-xlna

=xa-2a1-x(a-1-xlna).

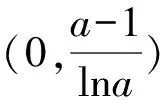
由0

g(1)=1+lna.

∀x∈(0,1),g(x)≥0,f′(x)=axg(x)≥0.

于是f(x)在(0,1)单调递增.

所以∀x∈(0,1),f(x)>f(0)=1.

x∈(0,x0),g(x)>0,x∈(x0,1),g(x)<0.

于是f(x)在(0,x0)上单调递增，在(x0,1)上单调递减．

又f(0)=1,f(1)=1+a>1,

所以∀x∈(0,1),f(x)>1.

g(x1)=g(x2)=0，

且x∈(0,x1)∪(x2,1),g(x)>0,

x∈(x1,x2),g(x)<0.

于是f(x)在(0,x1)上单调递增，在(x1,x2)上单调递减，在(x2,1)上单调递增．

由g(x2)=0,得

>1.

又f(0)=1，

所以∀x∈(0,1),f(x)>1.

证法1通过对g(x)分类讨论来探究f(x)的单调性，利用极值并结合端点处的函数值来证明结论．不等式a,b∈(0,1),ab+ba>1中含有两个变量a,b，证法1本质上是以其中一个变量为主元，通过函数方法来证明结论．

在给出证法2之前，先证明一个引理．

引理(伯努利不等式)当0-1时,(1+x)r≤1+rx.

证明令f(x)=(1+x)r-1-rx，则

f′(x)=r(1+x)r-1-r

=r[(1+x)r-1-1].

由0

于是x∈(-1,0),f′(x)>0,

x∈(0,+∞),f′(x)<0.

故f(x)在(-1,0)上单调递增，在(0,+∞)上单调递减．

所以∀x>-1,f(x)≤f(0)=0.

所以(1+x)r≤1+rx．

由引理，得

同理可得

证法2通过变形后利用伯努利不等式来证明结论，思路非常巧妙．

当a→0+,b→1-时，ab+ba→1，所以1是f(a,b)=ab+ba,a,b∈(0,1)的下确界．

若增加变量c，则f(a,b,c)=ab+bc+ca,a,b,c∈(0,1)的下确界是多少？ab+bc+ca>1是否成立？本文经过探究，得到以下结论：

结论1 当a,b,c∈(0,1)时,ab+bc+ca>1．

证明由轮换对称性不妨设a=min{a,b,c}，

则a≤b.

由0

ca≥cb.

所以ab+bc+ca≥ab+bc+cb>ab+1>1.

则a,b,c∈(0,1)，且

当n→+∞时，ab+bc+ca→1，

所以1是f(a,b,c)=ab+bc+ca,a,b,c∈(0,1)的下确界．

实际上，变量个数为n(n≥4)时，结论也成立．于是得到一般性结论：

证明由轮换对称性不妨设

a1=min{a1,a2,…,an}，

则a1≤an-1.

由0

a2=f(a1),

a3=f(a2),

…

an-1=f(an-2),

则当k→+∞时，a1→0,

a2=f(a1)→0,

a3=f(a2)→0,

…

an-1=f(an-2)→0,

an→1.

所以当k足够大时，a1,a2,…,an∈(0,1)．

当k→+∞时，

……

于是当k→+∞时，