改进Q学习的薄壁结构3D打印路径规划

王 祎，葛静怡，薛昕惟，王胜法，李凤岐

1.大连理工大学 国际信息与软件学院，辽宁 大连 116620

2.大连理工大学 软件学院，辽宁 大连 116620

3D打印技术也称增材制造技术（additive manufacturing，AM），是指融合了计算机辅助设计（computer aided design，CAD）、计算机辅助制造（computer aided manufacturing，CAM）、计算机数字控制（computer numerical control，CNC）和材料科学等一系列技术，通过将塑料、金属、粉末等材料层层堆叠形成目标实体[1]。经过几十年的快速发展，3D打印技术已广泛应用于医疗、航空航天、教育等领域[2-3]。当前，最常用的3D打印方式是熔融沉积（fused deposition modeling，FDM）打印，通过对目标模型进行切片，逐层打印并从下至上累积最终获得目标实体。在打印单层切片的过程中，打印喷头的运动路径规划是核心环节。良好的路径规划可以显著提高打印的性能，如何提高成型效率，保证成型精度是其中的重点研究方向[4]。

薄壁结构使用微少的轻量材料即可承受较大的载荷。18世纪中叶，薄壁结构被广泛用于建造箱形金属桥、船舶和车辆。1930年起，薄壁结构成为飞行器主要采用的结构形式，其在平滑流线的塑造，抗变形和承载能力方面具有很大优势。此外，薄壁轴承可实现极薄的轴承截面，确保了轻量和布线空间。近年来，薄壁结构的理论分析和实验研究不断增加，使其在工程中得到广泛应用。

用于3D打印路径规划的传统方法在打印薄壁结构时存在着一些问题。比如，ZigZag算法由于打印方向平行因而容易集中应力[5]，这种应力会影响材料散热，使模型容易发生变形甚至断裂；同时，喷头频繁的转弯行为会对成型质量造成一定的影响。轮廓偏置算法[6]是通过模型轮廓偏移生成扫描矢量，然后在内外方向上扫描成型。由于扫描线方向的不断变化，零件的内部应力方向发散并符合传热规律，从而避免了应力集中和阶梯效应，但可能因扫描间距差异而导致轮廓环相交，此外喷头较多的启停次数也会降低成型质量。王腾飞[7]提出基于等距偏移算法的路径规划方法，提高了成形件的精度和强度。分区扫描是把待扫描区域按照一定的规则分成若干个小区域，在一个小分区加工完成后快速移动到下一个分区进行扫描，这种扫描方式减少了空行程的数量，提高了成型效率[4]。程艳阶[8]对SLS成型进行了研究，提出了改进的分区算法，减少了分区的数量。连续的费马螺旋线能够形成较长且曲率低的路径[9]，其特殊几何特性能够提高分层打印的成型质量和效率。打印过程中喷头启停时的空程会导致制造效率和成型质量下降，为减少空程，Lensgraf等[10]提出了一种基于局部搜索的算法，并利用线性规划优化了路径方案。Panchagnula等[11]提出了一种用于打印复杂薄壁金属结构的方法，通过增加沉积头的自由度并利用高阶运动学，使悬垂特征与沉积方向成直线对齐来实现。Jin等[12]提出了一种薄壁零件路径规划方法，采用波浪形状填充细长截面，具有良好的沉积效果和较高打印效率。欧拉路径是图中的一种路径，该路径恰好访问图的每个边一次，Fleury算法[13]是欧拉路径的一种遍历方法，该算法始终在遍历期间选择非桥，以便返回到顶点并继续遍历其余边，适用于解决复杂薄壁结构的路径规划问题。

强化学习被广泛用于机器人控制、游戏和智能交通等领域[14-15]。其中，Q-learning指智能体在未知环境中进行无监督学习的过程，通过给予智能体奖励指导其行动，使其不断学习来做出最佳决策[16-17]。Q-learning可以适用于薄壁模型的打印。首先，智能代理可以通过感知周围的环境决定下一步行动来自适应地改变打印方向并提高打印效率。此外，Q-learning可以设置关于3D打印性能方面的约束条件，使智能体获得奖励以指导操作，以优化打印性能。

提出一种基于强化学习的复杂薄壁结构3D打印路径规划方法。这是目前关于3D打印的路径规划问题的已知研究中首次应用强化学习方法。首先，将强化学习中常规的路径规划问题转化为路径的全遍历问题，然后根据3D打印的特性设计Q-learning的约束条件来控制打印头启停和转弯次数，通过路径规划训练实验寻找最佳规划方案。实验结果表明，与用于3D打印路径规划的传统方法相比，该方法可以显著减少打印头的启停和转弯次数，从而提高成型质量，同时还可提升打印效率。

1 基于Q-learning的路径规划算法

1.1 算法概述

3D打印的过程整体上分为四部分：（1）利用建模软件建立3D模型；（2）利用切片软件对3D模型进行切片；（3）对3D模型的单层切片进行2D路径规划；（4）路径填充后的切片经过逐层堆叠形成模型实体。提出的方法用于处理（3）中的路径规划部分，具体流程设计见图1。

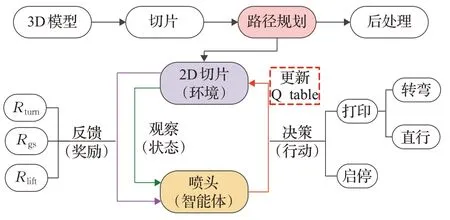
图1 基于Q-learning的路径规划方法流程图Fig.1 Procedure of Q-learning-based path planning method

提出一种基于Q-learning的智能路径规划算法（Qpath）。根据FDM打印系统的特点，将打印喷头作为智能体，2D切片作为环境，喷头通过观察切片环境获取当前状态和下一步动作等信息，并根据设计的针对转弯和启停次数的约束条件做出决策。每次做出的决策会更新Q表，该表用于评估状态-行为对，并通过决策获得的奖励指导喷头的后续动作。喷头通过这种方式多次学习，寻找拥有最大总奖励的最佳路径规划方案。

1.2 仿真环境

将薄壁模型的STL文件切片为Ci(i=1,2,…,k)，将Ci中优化后的离散二维空间Ii作为路径规划的仿真环境。切片软件提取平面与网格模型上小三角面片的交线，为了减少计算量，将这些交线简化，只保留其中的拐点、交叉点及端点，称为打印控制点。图2（a）表示一个目标模型中某层切片Ci的打印仿真环境Ii及打印控制点（蓝色点表示）。

1.3 Q-path算法

首先建立Q-learning和3D打印要素之间的关系。将打印喷头作为Q-learning中的智能体，仿真环境Ii作为环境，打印头的当前位置即是智能体的状态，下一个要打印的点则是智能体的动作。路径规划的主要任务是在一系列约束条件下，连接具有相邻关系的打印控制点来完成对Ii遍历。

在Q-learning中设计了两个约束条件以优化打印性能。首先，打印过程中的转弯行为会造成材料堆积，影响切片层厚从而影响成形质量。因此设计约束条件为当智能体进行转弯时根据转弯角度获得一定的负奖励，以控制转弯的影响。定义奖励函数Rt(spre,s,a)用于计算上一步的位置是spre的情况下，从当前位置s执行动作a获得的奖励，元素间位置关系见图2（b），函数见式（1）：

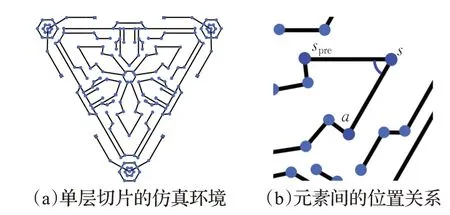
图2 仿真环境Fig.2 Simulation environment

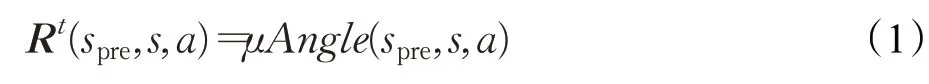
式中，Angle(spre,s,a)为向量spres和sa的夹角，μ是一个负常数。可以看出，执行动作a获得的负奖励随着与当前方向spres的偏差的增加而增加，方向不改变则不会获得负奖励。另一方面，打印头的启停次数也是影响打印效率和成型质量的因素之一，喷头的空程不仅耗费时间，还会造成材料拉丝和堆积，因此喷头启停行为的成本比转弯行为的成本更高。设计约束条件为当智能体进行启停时根据空程距离获得一定的负奖励。当处于状态s，没有可选的动作a时，智能体会选择并直接转移到距离最近的状态s͂，定义奖励函数Rl(s,s͂)用于计算启停行为获得的奖励，见式（2）：

其中，πμ是式（1）中Rt的最大值，即最大角度的转弯惩罚。由于启停行为会造成两处材料堆积，且堆积程度相对转弯行为高，因此2πμ代表启停行为关于材料堆积方面的惩罚。ν是一个负常数，Dist(s,s͂)是启停点s和s͂之间的欧式距离，因此这部分代表空程导致的效率降低及拉丝的方面惩罚。

建立行动-效用矩阵Q(spre,s,a)，假设在某个策略下某个状态的后续行动是已知的，则该矩阵存储的元素在上一个状态是spre的情况下，在状态s执行动作a所获得的累积奖励。初始化Q中元素为0。优化目标为最大化单层切片的总奖励。为寻找全局优化方案，采用ε-Greedy方法：以ε的概率探索，以1-ε的概率利用，状态转换公式见式（3）、（4）。若在ε的概率下选择了动作a，则有：

关于终止条件，Q-learning中是智能体在Q矩阵中不断进行状态转移，直到到达约定的最终状态，过程中不限制某个状态被选择的次数。然而3D打印中路径规划的基本目标是打印所有路径，因此将终止条件设为所有状态都被无重复地遍历。设定一个列表L来存储所有状态，每当执行一次动作时，从L中删除该状态，不断执行动作直到L为空，以防止后续动作再次选择已遍历状态，从而避免在打印过程中重复遍历。关于起终点的设置，由于获得最佳起点需要将环境中的所有状态分别设置为起点，比较每条路径的总成本来选择最佳起点，但这种方式会导致过高的时间成本，因此随机选择起点。由于Q-path寻找最佳路径方案的过程是完全智能的，因此在遍历问题中终点无法被预先设置。

2 实验结果与分析

采用Zigzag算法（Zigzag-path）、Fleury算法（Fleurypath）作为对比算法，从转弯次数、启停次数以及打印时长三个方面测试Q-path算法的性能。所有实验均在Python 2.7环境下实现，运行环境为3.40 GHz CPU和8 GB RAM的Intel®Core（i）i7。式（1）～（4）中参数取值：ε=0.3，γ=0.9，μ=1/π，ν=0.2。

2.1 薄壁结构

在多个不同薄壁结构的环境下评估Q-path、Zigzagpath和Fleury-path的性能。首先以图2中的模型1为实验目标。图3描述了Q-path训练出的路径打印过程，红色圆点表示起点，红色箭头表示打印过程中喷头的实时位置，实验结果的统计数据如图4所示。可以观察到，传统的Z-path的表现和另外两种算法的表现差距较大。由于Zigzag-path的自适应性较弱，不能将启停次数控制在较低的水平，从而付出了较多的启停次数来代偿转弯次数，因此转弯次数最少，启停次数最多。然而按总成本计算，Zigzag-path的成本最高，因为单次启停行为的成本至少是转弯行为的成本的2倍，因此其较弱的自适应性导致了总体性能下降。从打印总路程（包括空程）长度来看，Q-path和Fleury-path在时间效率方面的表现明显好于Zigzag-path。由于Q-path具有全局性，其总体表现比Fleury-path稍好，总成本最低。

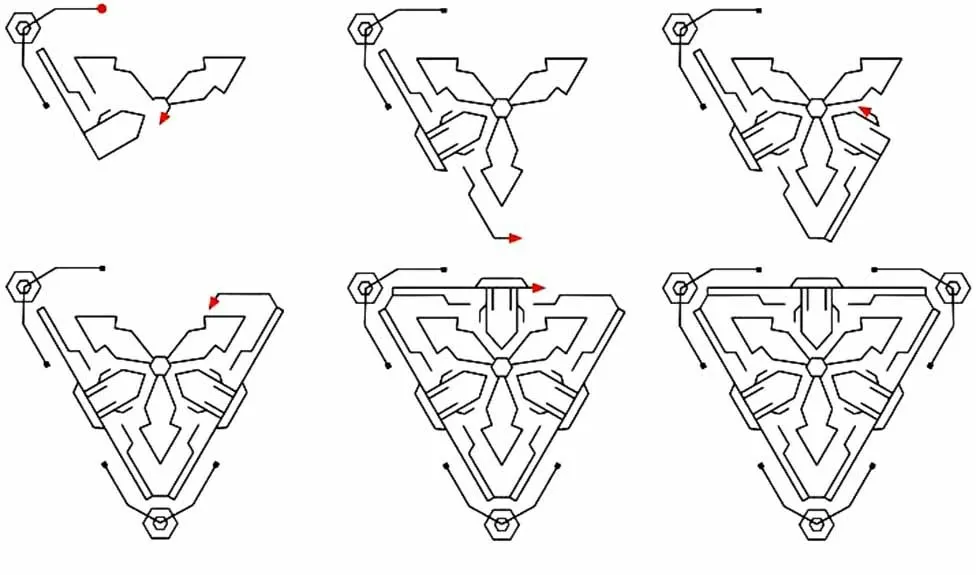
图3 Q-path对模型1的路径规划过程Fig.3 Path planning process of Q-path for model 1

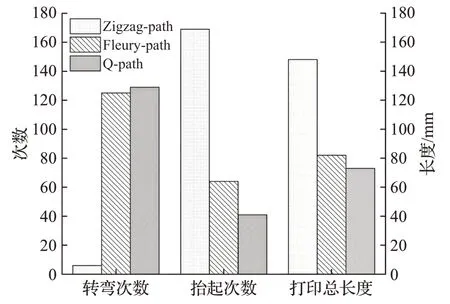
图4 三种算法对模型1的路径规划结果Fig.4 Path planning results of three algorithms for model 1

选取一个通路数量更多的薄壁结构模型2，图5显示了Q-path的训练结果的路径规划过程。Q-path及对比算法的性能数据统计如图6所示。综合上一个实验分析得出，Fleury-path和Q-path由于相对灵活而稳定性较高，传统的Zigzag-path算法依然不能较好地适应复杂薄壁结构。对于Fleury-path和Q-path的性能差距，分析Fleury-path路径规划的过程得出，当Fleury-path建立欧拉回路时可能会多次经过某个位置，打印头首次经过的行为是打印该点，但二次经过该位置时，需执行启停动作以跳过该位置继续打印，从而打印过程后期会造成较多的启停次数。而Q-path的智能性更强，考虑到全局优化，通过设置成本开销最高的启停行为获得最高的惩罚，从而将总启停次数控制在低水平，同时提高了打印效率。因此Q-path在此实验模型上表现依然最佳。

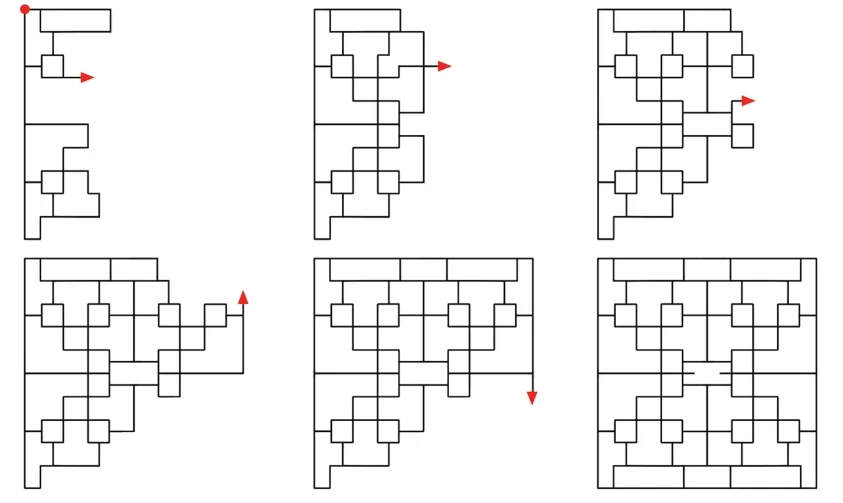
图5 Q-path对模型2的路径规划过程Fig.5 Path planning process of Q-path for model 2

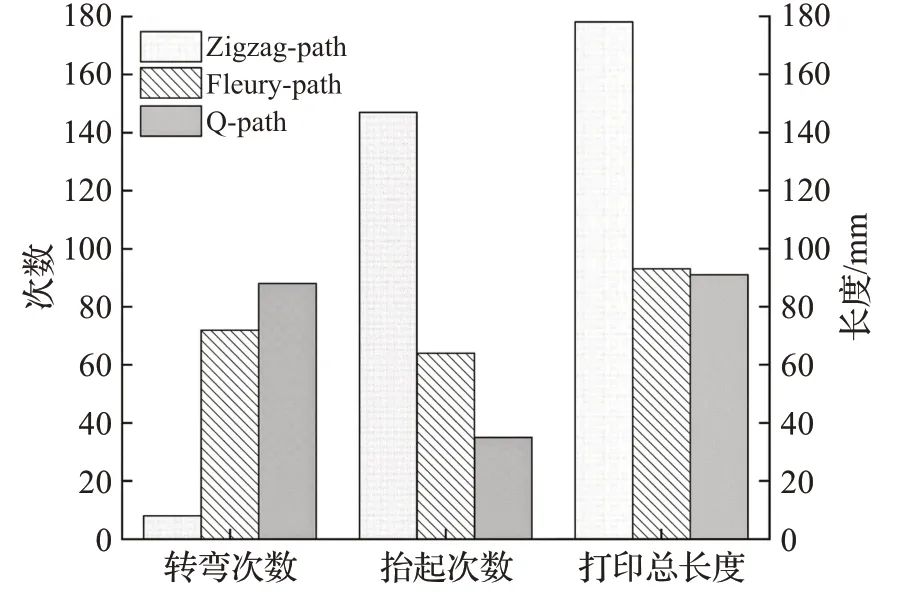
图6 三种算法对模型2的路径规划结果Fig.6 Path planning results of three algorithms for model 2

2.2 结构复杂程度

比较算法的性能随着薄壁结构复杂程度增加的表现情况，选取具有不同复杂程度n（n为模型包含正方形的数量）的模型，如图7所示。图8显示了三种算法的性能数据统计结果。可以看出，Zigzag-path算法的总成本仍然是最高的。Fleury-path与Q-path的性能数据相似，但计算得出的总成本比Q-path略高。数据显示当模型复杂程度为n=5时，Fleury-path的转弯次数要低于Q-path，这是由于2.1节中所述的Fleury-path容易多次访问同一位置的特点，启停次数则会代偿转弯次数，因此有时转弯次数可能较少，但总成本仍比Q-path高。随着模型复杂度的增加，Q-path总成本的提升率最低，证明了Q-path在处理复杂模型时具有较好的稳定性。

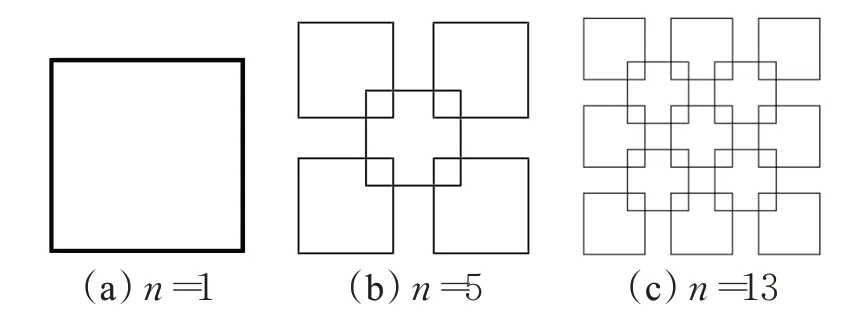
图7 具有不同复杂程度的薄壁模型Fig.7 Thin-walled models with different complexity

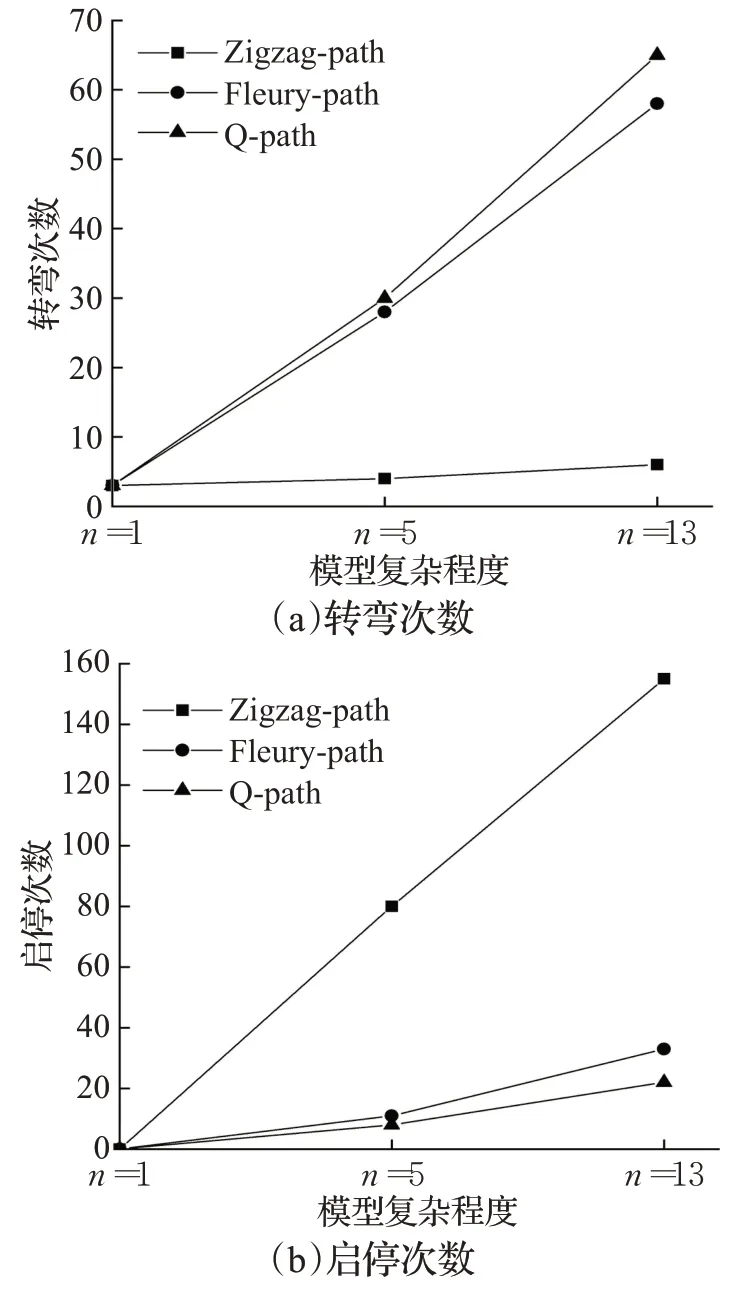
图8 三种算法在模型复杂程度增加过程中的性能变化Fig.8 Performances of three algorithms change as complexity of model increases

2.3 整体打印效率

实验角度从单层切片收缩到模型整体。由于Q-path采用了强化学习方法，在得到打印结果前需要预先进行训练，因此比较算法的路径规划时间成本需要考虑训练时间。假设模型每层切片的结构都是相同的，采用图2中的模型进行实验。结果如图9所示。其中Q-path的时间成本包括训练时间和打印时间。可以看出，随着模型层数的增加，Fleury-path和Q-path的时间成本增长速率明显比Zigzag-path慢。当模型只有一层时，Q-path的时间成本要比Fleury-path高，是因为Q矩阵的训练时间，而训练时间取决于该切片所包含的数据量。但当模型具有较多层时，Q-path花费的时间最少，该算法的优势得以体现。在实际工程应用中，模型通常层数较多，因此Q-path是一种比较节约时间成本的解决方案。

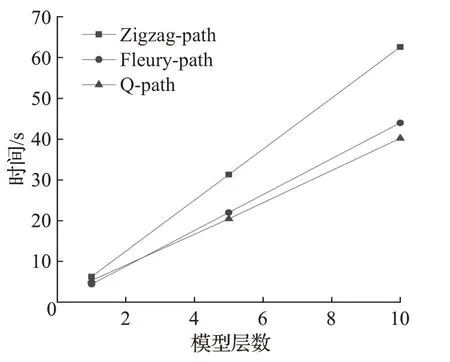
图9 三种算法对模型2的路径规划结果Fig.9 Path planning results of three algorithms for model 2

3 结束语

由于用于3D打印路径规划的传统方法对薄壁复杂模型的适应性较弱，因此将强化学习应用于3D打印领域，提出了一种新颖的适用于薄壁复杂结构模型的路径规划方法。设计多个打印约束条件以优化打印性能，采用Q-learning算法寻找约束下的最佳路径方案。实验结果表明，与用于3D打印路径规划的传统方法相比，该方法有效提高了3D打印的效率和性能，并且算法的性能随着模型复杂程度的增加能够保持稳定。作为需要预先训练的强化学习方法，Q-path比较适用于每层结构相同的复杂薄壁模型。未来的工作将主要集中在针对具有不同层结构的模型的智能打印算法的研究，并结合传统的打印方法，分区方法以及模型的物理性能优化方法来扩展智能打印算法的应用范围。