面向旋转机械故障诊断的深度流形迁移学习

邱颖豫，张 柯，杨欣毅

许昌学院 信息工程学院，河南 许昌 461000

航空发动机、汽轮发电机组、离心式压缩机等旋转机械设备是交通、电力和机械制造等重要行业的关键设备。开展旋转机械状态监测和故障诊断不但有利于降低维修成本，保障设备安全可靠工作，更能有效预防重大事故。因此，旋转机械故障诊断技术研究具有重要的实际意义和研究价值。

近年来，基于人工智能的方法逐渐成为旋转机械故障诊断领域的重要研究方向[1]。其中深度学习方法取得了比反向传播神经网络（back propagation neural network，BPNN）、支持向量机（support vector machine，SVM）和极限学习机（extreme learning machine，ELM）等浅层模型更好的结果[2]。多种深层网络模型，如深度置信网络（deep belief network，DBN）[3-4]，堆叠自编码器（stacked auto encoders，SAE）[5-8]，深度卷积网络（deep convolutional neural network，DCNN）[9]被广泛应用于故障诊断。

然而这些方法的训练和测试数据均在相同工况下采样，服从相同分布。而实际旋转机械的工况，尤其是转速和负载变化将导致数据概率分布的变化[10]，此时，统计机器学习的独立同分布假设被破坏。若将在源域训练好的分类器直接应用于目标域，将导致诊断精度严重下降。例如在文献[7]中，当测试数据对应的负载与训练数据差别较大时，滚动轴承的诊断精度从99.57%下降到88.27%。

迁移学习为解决诊断模型缺乏领域适应能力的问题提供新的途径。迁移学习[11]的目标是将某个领域学习到的知识或模式应用到相关但不同的领域[12]。一些研究将迁移学习和浅层模型相结合，如文献[13]利用TrAdaBoost算法，提高了变转速、负载条件下电机故障诊断精度；文献[14]提出一种基于辅助数据迁移学习的增强型最小二乘支持向量机，提高了变工况轴承故障诊断精度；文献[15]提出一种领域适应的极限学习机来解决传感器漂移引起的诊断性能下降。然而这些研究均采用浅层模型，表征能力有限；并需要一定数量的目标域带标签样本来辅助诊断知识迁移。但对于实际的旋转机械故障，故障模式是未知、无法提供目标域标签信息。

为解决目标域无标签情况下领域间概率分布失配问题，文献[16]引入最大均值差异（maximum mean discrepancy，MMD）来度量不同领域数据的分布差异，并将其加入浅层神经网络的优化目标函数，提出领域适应神经网络（domain adaptive neural network，DANN）。由于计算MMD无需目标域标签，该方法具有更好的适用性，在多个跨领域图像分类任务中取得最高精度。文献[17]则提出利用多核最大均值差异（multi-kernel MMD，MK-MMD）来度量概率分布差异，并将MK-MMD和深度学习相结合，在分类器预训练和微调阶段的优化目标均加入MK-MMD作为正则项，在多个迁移分类任务中取得最好的结果。文献[18]针对滚动轴承故障诊断，提出一种深度适配模型：以一维卷积网络为框架，采用MMD和度量学习来消减领域间特征分布分布差异。文献[19]则以深度稀疏降噪自编码器为模型框架，提出一种MMD正则的精调的优化目标，并设计相应的优化算法。该方法在旋转机械故障诊断应用中取得最高精度。

然而，基于MMD的领域适配的本质是对齐不同领域均值的中心，上述方法均未考虑到特征分布的流形结构，面对不同工况下复杂的机械故障信号，其适配性能不足。以图1所示情况为例，如仅适配领域的均值中心，则源域的分类界无法准确的对目标域数据进行分类。而如果同时适配均值中心和流形结构，则可利用源域分类界面准确的对目标域数据进行分类。

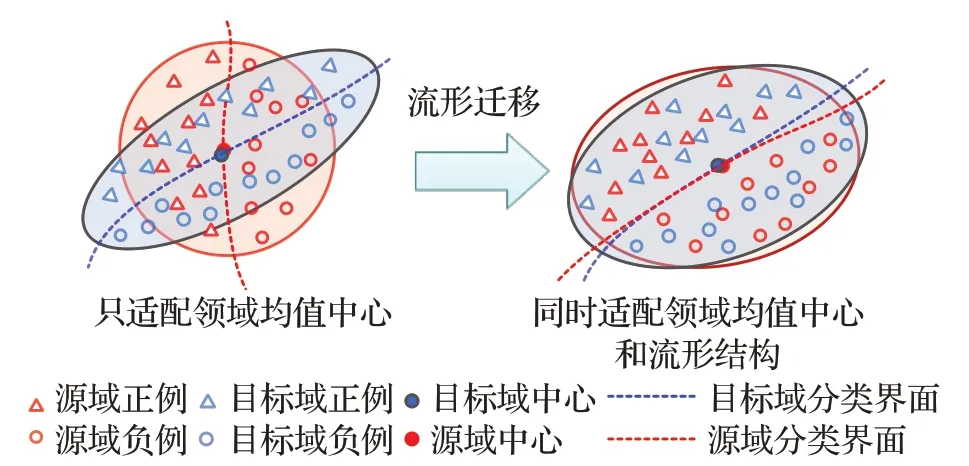
图1 流形迁移示意图Fig.1 Structure of AE

基于上述思想，为解决现有迁移学习方法的不足，本文提出一种同时适配领域间数据概率分布及流形结构的新方法—深度流形迁移学习（deep transfer learning，DMT），基于SAE结构，首先在无监督预训练阶段同时挖掘源域和目标域样本的数据特征；在微调阶段，则通过新的目标函数，同时适配领域间分布差异和特征分布的流形结构。对轴承及齿轮故障数据的诊断结果表明：新方法对工况变化具有良好的泛化性能，其性能优于现有的迁移学习方法，能显著提高变工况下的故障诊断精度。此外新方法训练过程无需目标域数据标签及工况信息，具有良好的适用性。

1 深度流形迁移学习模型

本文以堆叠自编码器为基本框架，提出一种新的深度流形迁移学习诊断模型。以下分别对堆叠自编码器和深度迁移学习模型进行说明。

1.1 堆叠自编码器

自编码器（auto encoder，AE）[20]可视为三层无监督学习神经网络，由输入层、隐含层和输出层组成，如图2所示。AE通过在输出层重构输入来学习数据的本质特征，可用于数据降维。AE分为编码和解码两个部分，编码是从输入x∈Rm到隐含层h(x)∈Rn的映射：

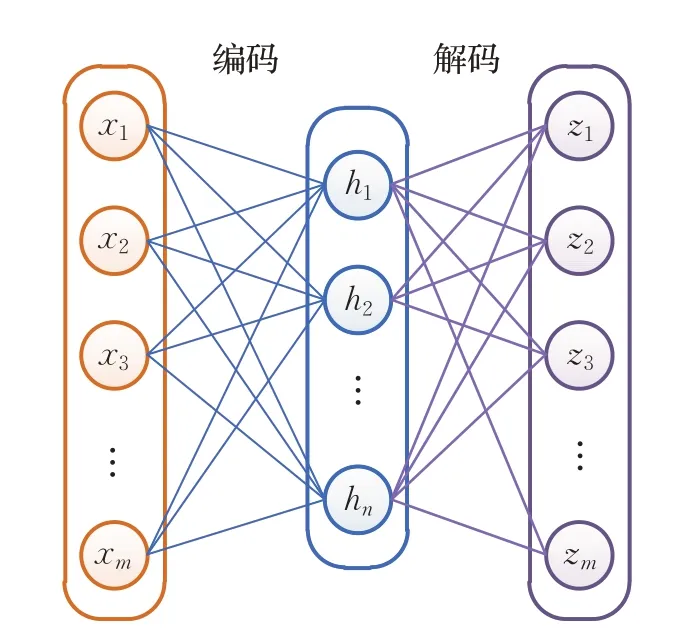
图2 自编码器结构Fig.2 Structure of autoencoder

其中，θ={W,b,W＇,b＇}为自编码器的参数。

将多个AE叠加在一起便可构造SAE。其中每个AE经过编码后的隐层输出作为下一个AE的输入，即构造过程只用到编码部分。最顶层的隐含层输出则作为深度特征输入分类器。SAE的训练包括两个阶段：第一阶段是对每个AE的无监督预训练；第二阶段是对SAE整体的有监督微调，通常采用小批随机梯度下降（minibatched stochastic gradient descent）等基于梯度的训练算法。

1.2 深度流形迁移学习模型

1.2.1 模型构建

现有的深度适配模型大都基于自编码器或者卷积神经网络等深度模型框架，通过在模型的目标函数中引入MMD或多核MMD正则项，在全部或部分隐含层最小化正则目标函数，实现源域和目标域特征的分布适配。

然而从MMD的经验计算公式（4）中可以看出。MMD仅仅对齐源域Xs和目标域Xt核特征映射的均值中心，没有考虑特征分布的具体结构。对于具有较为复杂流形结构的振动信号数据来说，仅适配领域均值中心是不够的。

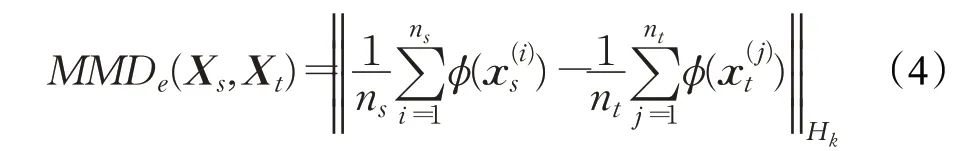
式中，φ()为将变量映射到再生核希尔伯特空间的核函数。为更准确地拟合领域间的分布，本文提出一种新的深度流形迁移模型：在适配领域间均值中心的同时，还要保持域内特征的分布结构不变，充分挖掘源域和目标域数据分布所隐藏的结构信息，以进一步提高诊断精度。

根据流形理论，数据通常位于高维空间中的某一潜在低维流形结构之上[21]，若样本xi、xj在边缘分布Ps(xi)和Pt(xj)的流形上相似，由于条件分布在流形的测地线上是光滑变化的，因此它们的条件分布Qs(y|xi)、Qt(y|xj)也应该相似[22]，相应的，模型也具有类似的输出。基于上述假设，利用源域和目标域数据共同构造流形正则项：

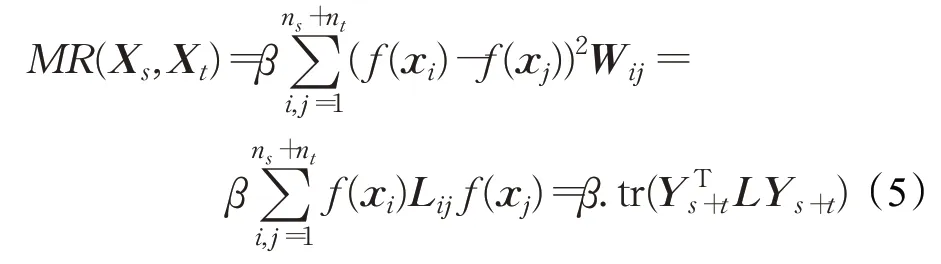
式中，f(xi)表示样本xi经过深度模型的输出，其中W是图邻接矩阵：

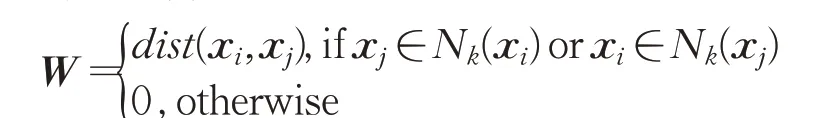
Nk(xi)为样例xi的k-近邻集合，L是由源域和目标域样本共同计算的拉普拉斯矩阵L=D-W，D为对角矩阵，其对角元Dii=∑jWw,ij,β是经验系数，β=1/(ns+nt)2,Ys+t是两个域样本构成的输出矩阵。

将MMD适配和流形结构适配同时作为正则目标加入模型的优化函数，得到深度流形迁移学习的优化目标如式（6），其结构如图3所示。

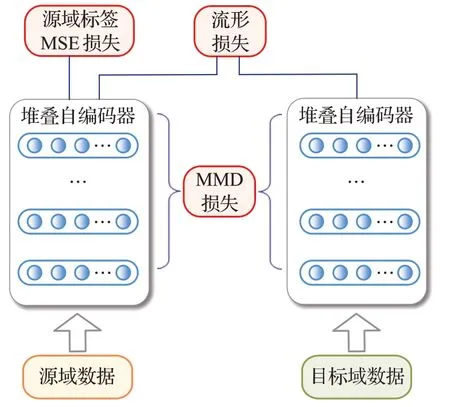
图3 深度流形迁移模型结构Fig.3 Structure of deep manifold transfer model

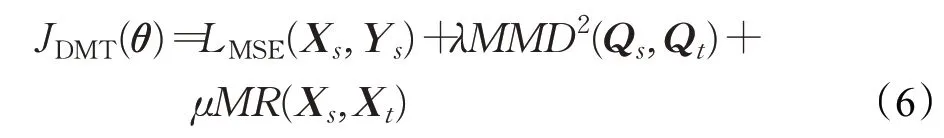
式中，LMSE(Xs,Ys)为定义在源域有标签数据上的均方误差损失函数。MMD2(Qs,Qt)为最大均值差异MMD的正则。需要指出的是，本文采用的是基于隐含层的带权输入Qs和Qt，而不是输出来计算MMD。因为带权输入在经过非线性映射后会在一定程度上改变概率分布形状[23]，因此采用Qs和Qt来比较领域间分布差异更为准确。λ和μ用于调节MMD正则和流形正则的重要程度。

1.2.2 模型的学习

（1）融合目标域的无监督预训练

DMT模型是由多个自编码器逐层叠加构成的。为充分挖掘各领域测试数据，对于每一个自编码器的预训练，采用平方误差函数。在训练数据方面，本文提出同时利用源域和目标域混合样本进行训练。即，利用小批随机梯度下降训练时，每个样本必须包含同样数量的源域和目标域样本。这样在无监督预训练的阶段，可以利用模型同时挖掘不同领域的数据特征。

（2）流形迁移微调

将经过预训练的自编码器的编码部分逐层叠加，并在顶层设置softmax分类器，就构成DMT模型。对模型的微调，同样采用小批随机梯度下降训练，对于模型参数θ梯度更新可表示为：

式中G..下标“.”可以是源域或目标域，s为高斯核函数k(⋅,⋅)的带宽参数。

整个模型的训练过程可总结为算法1，在预训练阶段同时利用源域和目标域样本对网络参数进行初步学习，挖掘振动信号本质特征；在微调阶段则利用源域带标签样本及目标域样本进行流形迁移学习，以更好的适配领域间特征分布结构。在整个训练过程中都无需目标域样本标签或其他任何信息，满足实际故障诊断需求。

算法1深度流形迁移学习算法Xs,Ys

输入：源域数据样本及标签Xs,Ys，目标域样本Xt，深度网络深度L及各层节点数，MMD适配正则参数λ，流形适配正则参数μ，批训练样本尺寸Nm，预训练及微调阶段学习率、迭代次数

1.2.3 诊断流程

采用深度流形迁移学习模型进行故障诊断的流程包括：

步骤1在不同工况下开展各故障模式实验，将采集到的振动时域信号分割为等长度样本，并转换为频域样本。

步骤2将频域样本按照预设比例分为训练、测试和验证集合。

步骤3按照算法1利用源域和目标域数据样本训练深度流形迁移模型。

步骤4利用训练好的训练深度流形迁移模型对目标域样本进行故障诊断，输出识别结果。

2 模型在旋转机械故障诊断的应用验证

为验证所模型有效性，将其应用于变工况下滚动轴承和齿轮的故障诊断，并与目前主流的深度学习算法SAE，以及迁移学习算法DANN[16]、TDN[17]进行综合比较。

2.1 滚动轴承故障诊断

轴承故障数据采用美国凯斯西储大学（CWRU）滚动轴承数据中心的数据集。故障实验对象为图4中驱动端深沟球轴承SKF6205，设置有滚动体损伤，外圈损伤与内圈损伤三种故障模式，故障尺寸0.177 8 mm，采样频率为12 kHz。

图4 CWRU滚动轴承数据采集系统Fig.4 Rolling bearing data measuring system in CWRU

CWRU提供的数据文件（.mat格式）长度有限，因此采用重叠采样以生成更多时域信号样本。由于频域信号比时域信号更能展现设备特征[24]，本文利用频域样本作为模型训练测试数据。每个频域样本由时域信号样本经FFT变换得到。样本长度决定网络输入节点个数，对精度及算法复杂度也有重要影响[7，12]。本文在精度和训练时间中寻找平衡，通过实验确定时域信号样本长度为1 000数据点，则其对应的频域样本长度为500。

对正常及三种故障这四种模式，每种模式都生成2 000个样本，总计8 000个样本，测试、验证和训练样本比例为3∶1∶1。根据不同的负载及转速，选择四种工况，工况的说明见表1。迁移诊断任务用“Cm→n”表示，如“C2→1”是指利用源域（工况C2）的带标签训练样本和目标域（工况C1）的不带标签训练样本训练诊断模型，再去诊断C1的测试样本，整个训练过程只用到目标域训练样本，无需样本标签及其他任何信息。

表1 轴承故障实验的四种工况Table 1 Working conditions of rolling bear fault tests

被比较的方法中，SAE为经典的深度学习算法；DANN是首次将领域适应和神经网络相结合的算法。TDN则是近年来在跨领域图像和文本分类中取得最成功应用的深度迁移学习算法之一。其中TDN、SAE及DMT均为深层网络模型。TDN在文献[17]中采用了边际化栈式降噪自动编码器以加速训练。本文为公平比较，对TDN采用普通自编码器实现，三种深度学习算法均采用相同的深度网络结构、学习率、迭代次数等参数。而DANN为浅层网络模型，除网络结构不同外，也采用相同学习率、迭代次数等参数，所有算法的有监督训练均采用小批随机梯度下降算法训练。

具体的参数说明见表2，其中TDN采用多核MMD来适配概率分布：其中每个单核ku(xi,xj)=exp(-‖ ‖xi-xjαγ),γ=2s2,s为高斯函数的带宽参数，本文s均取值为训练样本的标准差，参数α则依次从[2-4,2-3,2-2,2-1,20,21,22,23,24]中选取。本文模型图邻接矩阵的近邻数k在验证集上实验确定取值。此外，模型还引入两个新的超参数λ和μ，这两个参数在验证集上通过交叉验证择优选择。所有算法的误差函数均统一设置为均方误差函数。

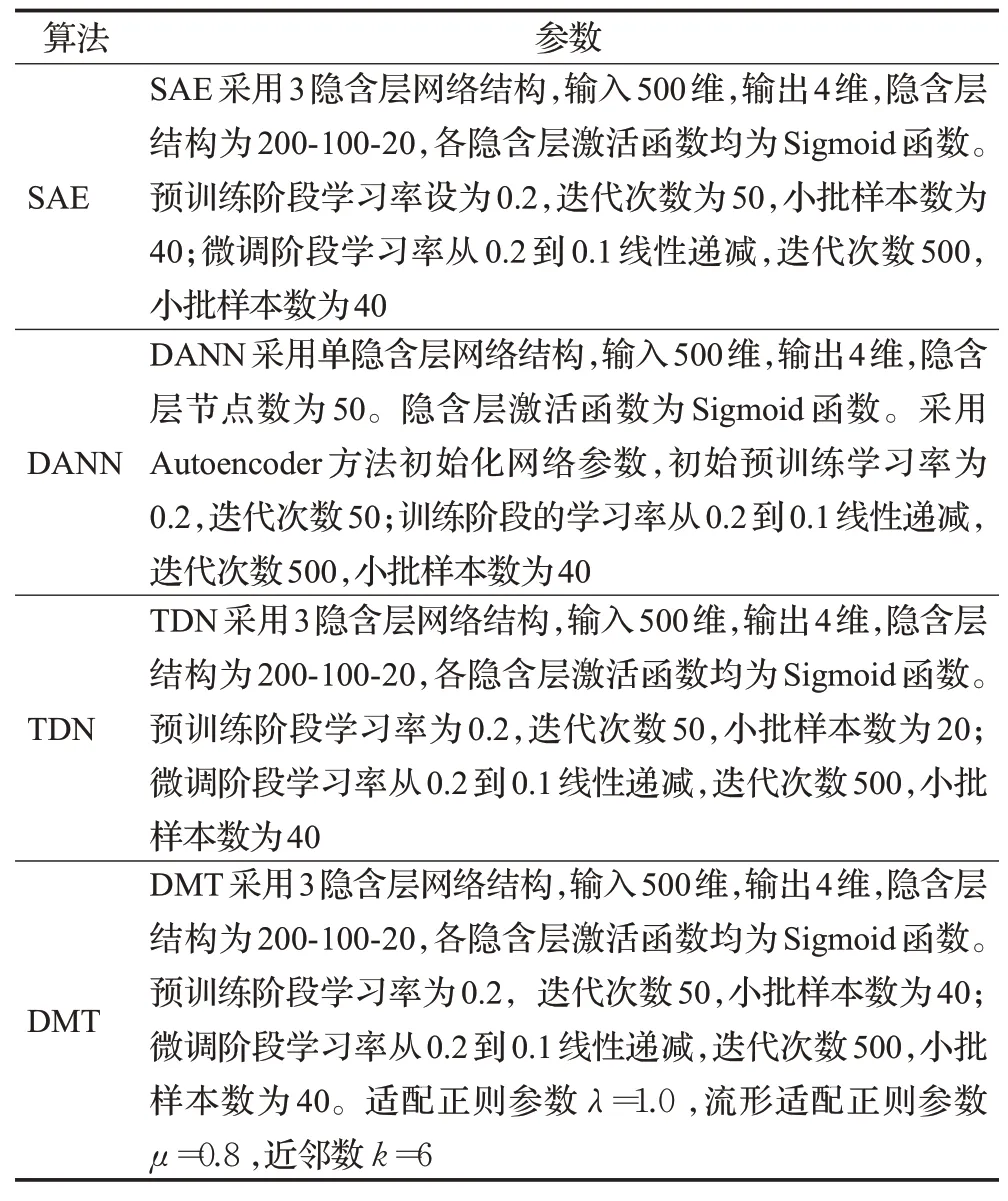
表2 各算法参数设置Table 2 Parameter setting of all algorithms

将各算法应用于CWRU轴承故障的迁移诊断任务。4个工况共计有12个迁移诊断任务，各算法独立运行10次的平均诊断精度及标准差（mean±std），如表3所示。

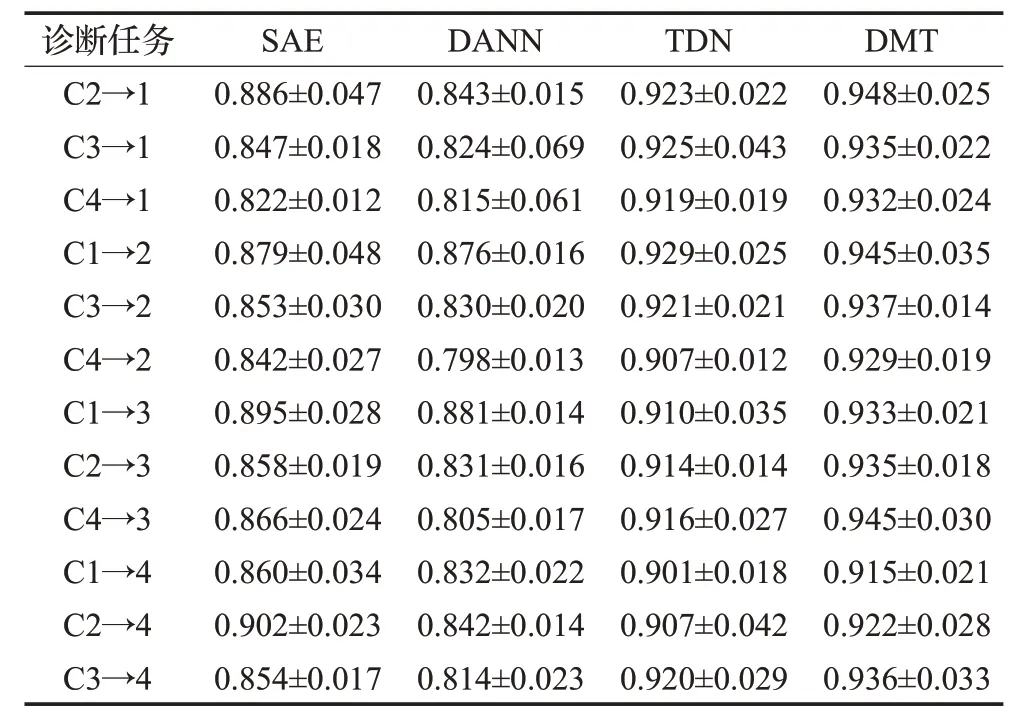
表3 各算法在CWRU数据集的迁移诊断结果Table 3 Fault diagnostic results by all algorithms on CWRU data set

从结果可见，本文方法DMT在所有变工况诊断任务上均取得最高精度，在12个变工况诊断任务上的平均精度为93.4%明显高于其他算法。TDN则取得次高平均精度，91.6%。三种深度学习方法中，DMT及TDN明显优于基本SAE。而DANN尽管进行了概率分布适配，但是其浅层结构限制了特征提取能力，所以其诊断精度仍低于SAE。

以上从平均精度的角度比较了各个算法，为更具体展现个算法性能，对C2→1诊断任务进行误差分析。图5所示为各算法对该任务的单次运行的误差结果。横坐标表示故障模式标签，纵坐标为该模式对应的未被正确分类的样本数。从图中可见，本文算法在变工况条件下对于正常、滚动体损伤，外圈损伤与内圈损伤这四种模式都能准确的分类，其误分类的样本数始终最低。而DANN的误分类数在所有故障模式均最高。此外可以发现相比故障的模式，正常模式的误分类数目普遍较低。

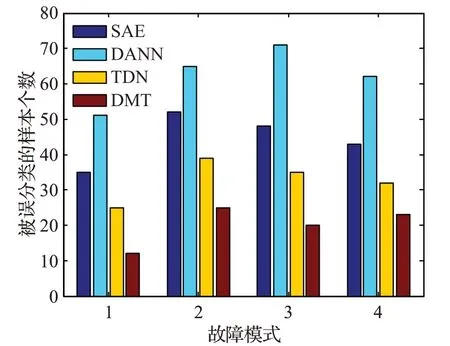
图5 各算法在C2→1诊断任务的误差Fig.5 Error analysis of all algorithms on C2→1 task

图6为微调阶段SAE及DMT对源域及目标域测试数据诊断精度随迭代次数的变化曲线。可以发现SAE尽管对源域测试数据的诊断精度提升很快，最终可以达到0.99以上的高诊断精度，但是对于目标域测试样本诊断精度不高。而DMT由于充分适配特征的流行结构，因此对源域和目标域的诊断精度都能随迭代有效增长，两者差距很小。

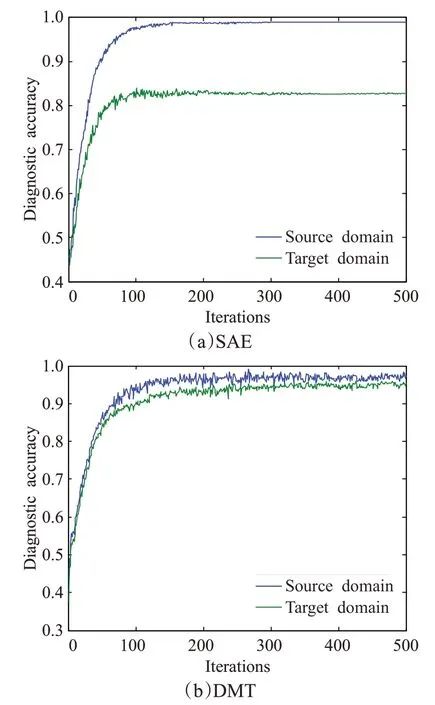
图6 两种算法微调阶段源域和目标域诊断精度变化Fig.6 Variations of target diagnostic accuracy with iterations in fine-tuning of two algorithms

2.2 齿轮故障诊断

齿轮故障的振动测试数据来源于图7所示的齿轮箱故障诊断综合实验系统。变速驱动电机为齿轮箱的转动提供动力，经过二级行星齿轮箱和二级平行齿轮箱传动，最后到达磁力制动器。驱动电机和磁力制动器由相应调节器来控制，用以变更不同转速及负载，从而模拟不同工况。实验台采用模块化设计，通过更换不同的齿轮故障件，能模拟多种齿轮故障。

图7 齿轮箱故障诊断综合实验台系统Fig.7 Synthetical fault diagnosis test bed of gearbox

图8为平行齿轮箱传动示意图，本文选择第二级平行齿轮箱中的齿轮G21为实验对象，开展故障模拟实验。模拟的四种故障分别为：断齿、缺齿、齿面磨损及齿根裂纹。

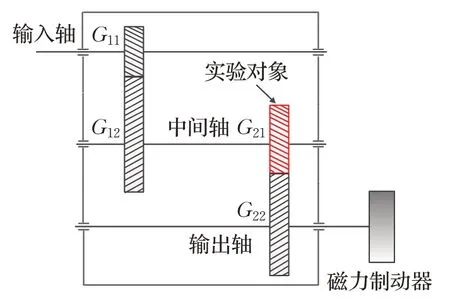
图8 二级平行齿轮箱传动示意图Fig.8 Diagram of second stage parallel gearbox

在三种工况下分别安装无故障的齿轮以及齿轮故障件开展实验，用安装于齿轮箱端盖处的PCB-355B03型加速度传感器采集齿轮故障数据和正常情况数据，采样频率为10 kHz。各工况的描述如表4所示。仍采用频域数据作为训练样本，每段样本包含500个样本点。对每个模式都生成2 000个样本，共10 000个样本，测试、验证和训练样本比例为3∶1∶1。

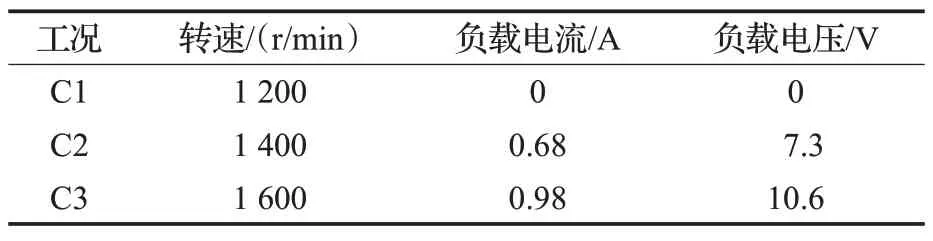
表4 齿轮故障实验的三种工况Table 4 Working conditions of rolling bear fault tests

各算法的参数设置除网络结构外，其他均与2.1节一致。三种深度学习算法的结构为500-200-100-50-5，DANN的网络结构为500-100-5。将各算法用于齿轮箱故障的迁移诊断任务。三个工况共计有6个迁移诊断任务。各算法运行10次的平均诊断精度及标准差如表5所示。从表中可以发现，对于所有诊断任务中，DMT均取得最高的诊断精度。再次验证了DMT模型的变工况故障诊断的优越性能。

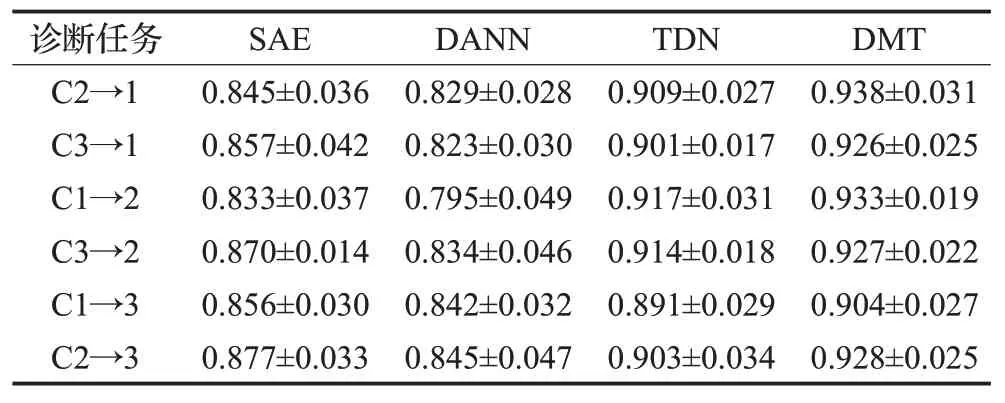
表5 各算法在齿轮故障数据集的迁移诊断结果Table 5 Fault diagnostic results by all algorithms on gear data set

而对C2→1诊断任务进行误差分析也可发现，DMT算法对于所有故障模式均具有最低的误分类样本数。进一步证明了其优越的故障诊断性能，如图9。

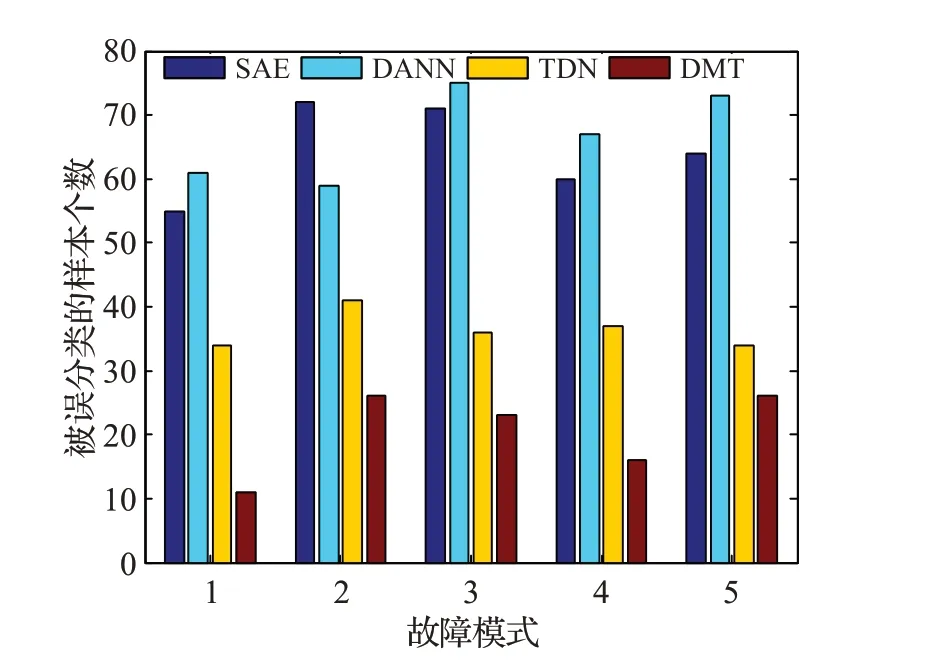
图9 各算法在C2→1诊断任务的误差Fig.9 Error analysis of all algorithms on C2→1 task

图10为对于齿轮故障SAE及DMT模型的微调阶段对源域及目标域测试数据诊断精度随迭代次数的变化曲线。如图10所示，SAE算法对于齿轮故障目标域样本的诊断精度始终和源域诊断精度保持很大差距。而DMT经过微调训练后对源域及目标域均能得到较高的诊断精度。

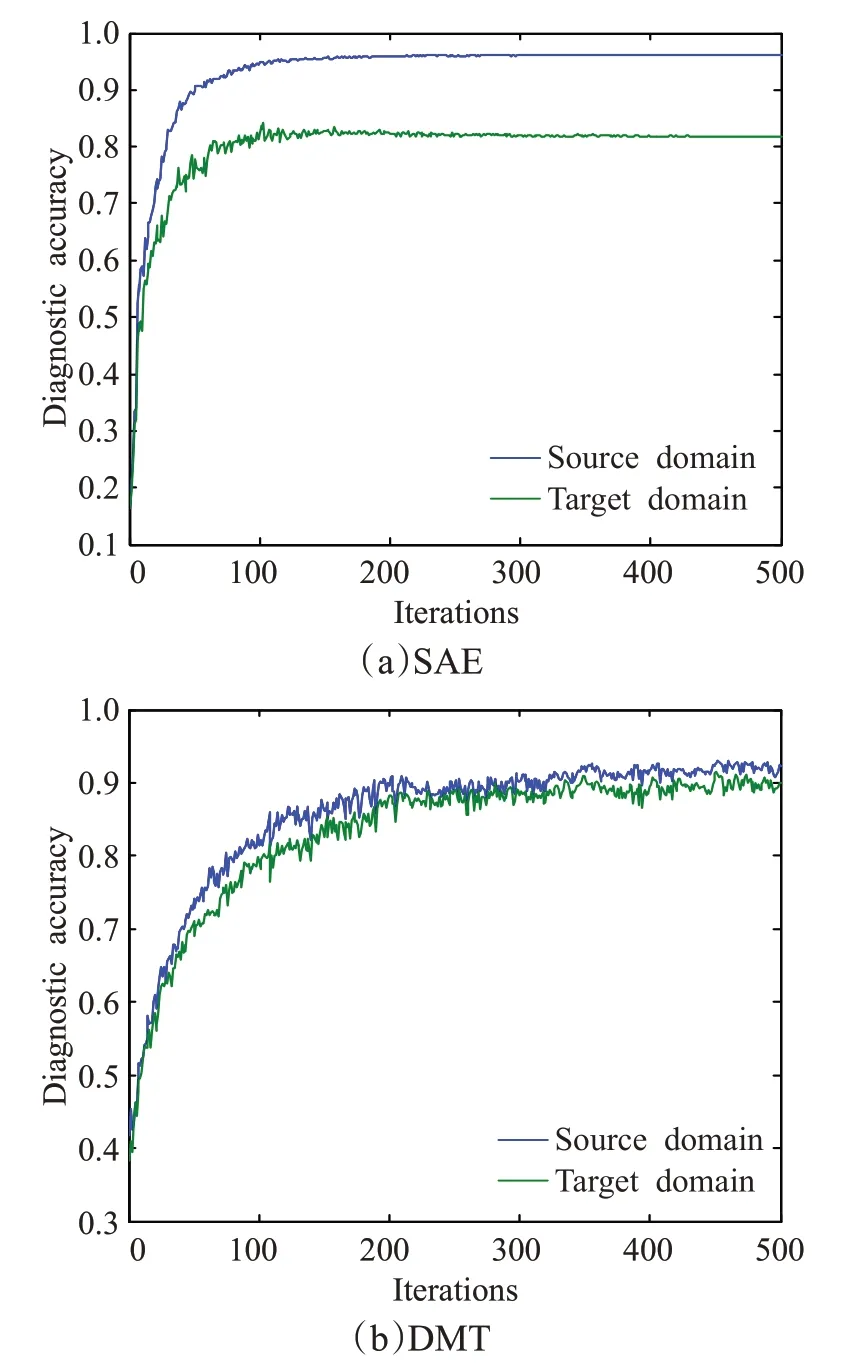
图10 两种算法微调阶段源域和目标域诊断精度的变化Fig.10 Variations of target diagnostic accuracy with iterations in fine-tuning of two algorithms

3 方法有效性分析

3.1 融合目标域无监督训练的有效性

为充分挖掘监测数据隐含信息，本文在模型的无监督预训练过程采用“源域+目标域”数据作为训练样本。为说明该策略的有效性，在模型中取消该策略，其他不变，将该简化模型记为DMT-1。将简化模型与DMT在齿轮故障数据集的结果进行比较，如图11所示。由图可见，DMT-1在所有任务上的精度都低于DMT。可见在预训练阶段引入目标域数据有助于更好地挖掘特征结构，提升变工况诊断精度。

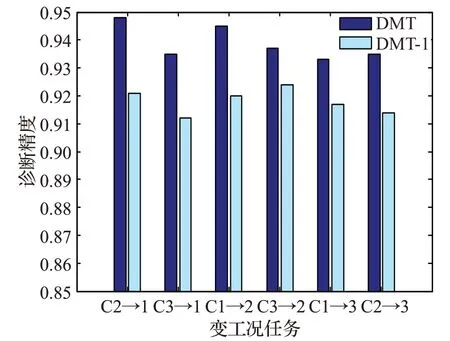
图11 采用目标域数据无监督训练对精度的提高Fig.11 Enhancement caused by using target domain data in unsupervised pre-training

3.2 流形迁移微调的有效性

不同于现有的深度迁移学习模型，本文在微调训练目标中加入流形正则，以保持特征分布结构不变。为说明其有效性，在模型中取消该策略，其他不变，将该简化模型记为DMT-2，将该模型与DMT在齿轮故障数据集的结果进行比较，如图12所示。图中DMT在所有任务上的精度都明显高于DMT-2，这个结果充分证明在领域适配的同时保持流形结构一致对针对精度的重要作用。

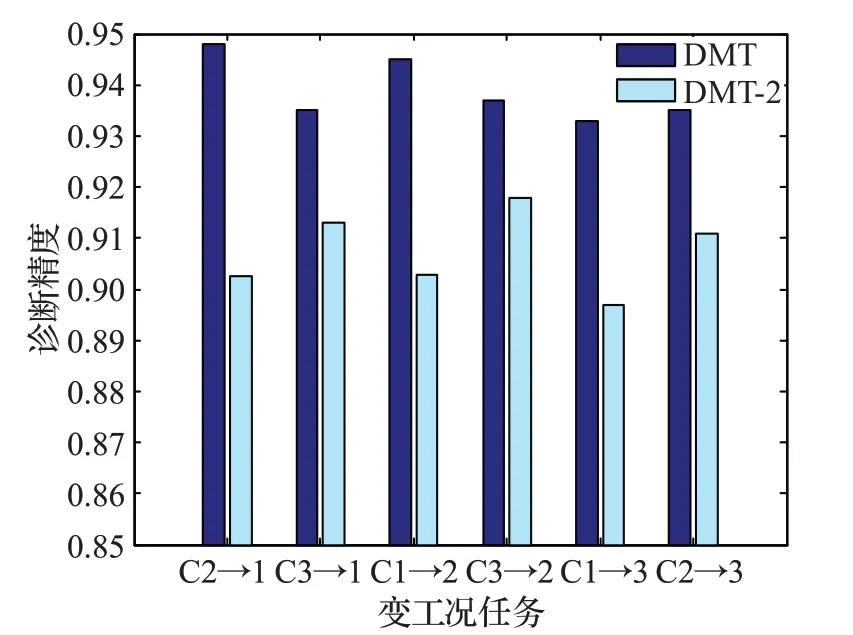
图12 流形迁移微调对精度的提高Fig.12 Enhancement caused by manifold transfer learning based fine-tuning

为进一步深入说明流形迁移对特征保持的有效性，以轴承故障数据的C2→1的诊断任务为例进行特征可视化。DMT-2及DMT模型经过完全训练后，分别将源域和目标域样本在模型最高隐含层的特征投影到二维PCA（principal component analysis）平面，其可视化结果分别如图13和图14所示。从图14中可以看，DMT模型更好地对齐了源域和目标域特征的结构，而图13中DMT-2的部分模式的源域和目标域在空间分布上存在一定的偏离。这是因为MMD只对齐领域的均值中心，无法考虑到具体的流形结构。可视化结果的对比充分证明流形迁移比传统的基于MMD正则的方法更能保持领域间特征结构的一致性。

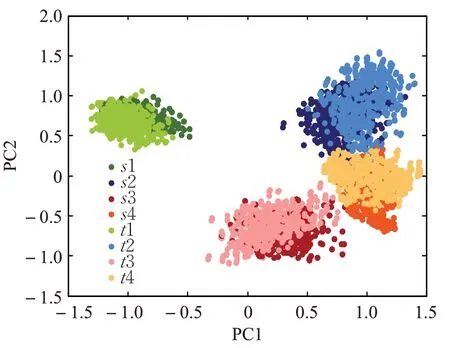
图13 DMT-2模型提取的样本高层特征二维可视化Fig.13 2D visualization of high-level features extracted by DMT-2

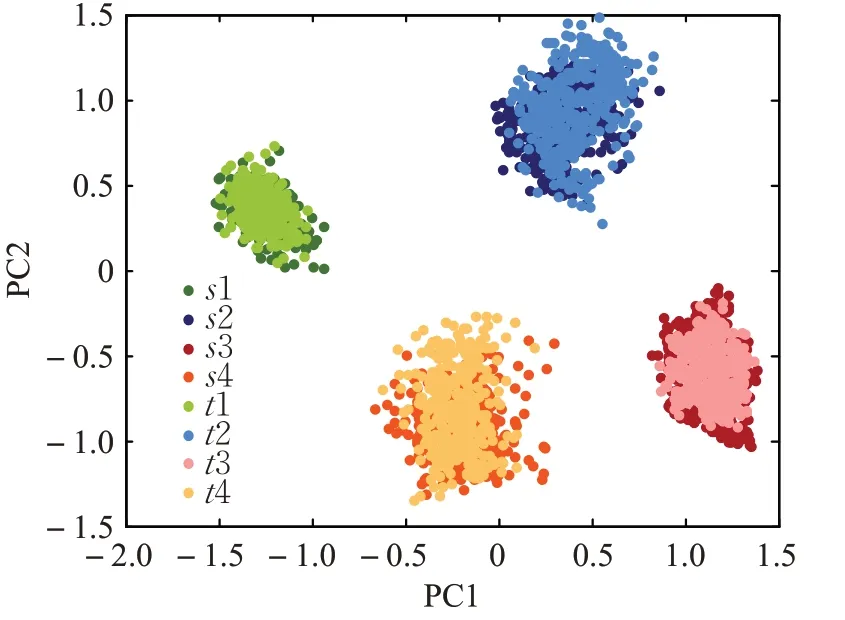
图14 DMT模型提取的样本高层特征二维可视化Fig.14 2D visualization of high-level features extracted by DMT

3.3 MMD适配的有效性

本文模型的优化目标中引入MMD正则，作为领域适配的基础。为说明其有效性，在目标中取消MMD正则，其他不变，将该简化模型记为DMT-3，将该模型与DMT的结果进行比较，如图15所示。图中DMT在各个任务的精度都高于DMT-3，该结果可证明MMD适配的重要作用。结合3.2节的分析结果，本文同时适配分布差异及领域间特征分布结构是十分有效和必要的。

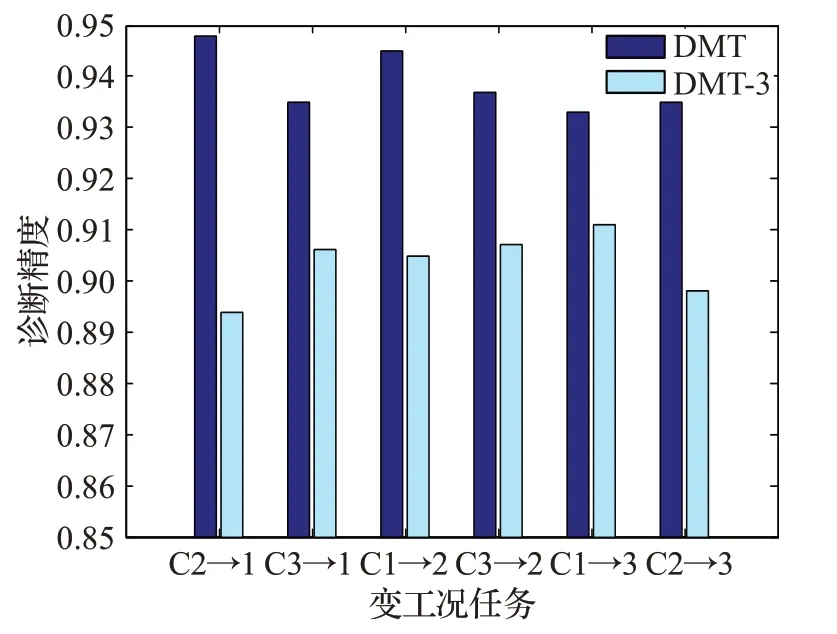
图15 MMD适配对精度的提高Fig.15 Enhancement caused by MMD regularization

4 参数敏感性分析

深度流形迁移学习模型在目标函数中同时引入λ和μ这两个参数用于调节MMD正则和流形正则的重要程度。这两个参数的取值对算法性能有较大影响。为此进行参数敏感性分析。在齿轮故障数据集的C2→1任务上，令两个参数分别在0.2至2.0范围内，以0.2等间隔取值，进行网格交叉，得到的诊断精度曲面如图16所示。从图中可以发现，当两个参数均大于0.8时，算法具有较高精度，且相对稳定。

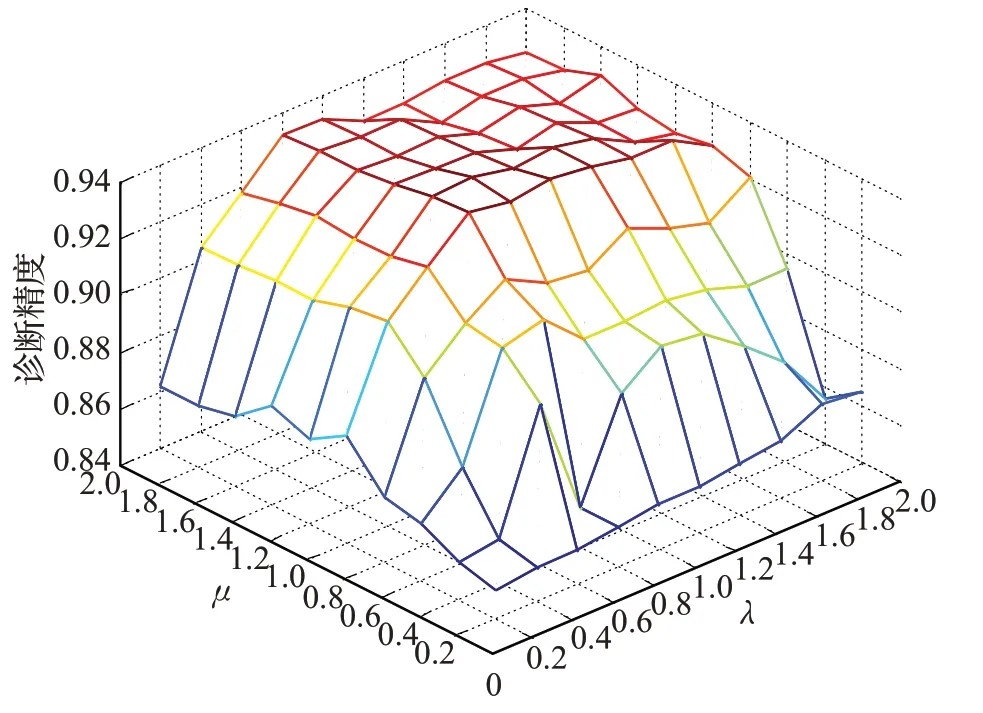
图16 参数λ和μ敏感性分析Fig.16 Parameter sensitivity analysis ofλandμ

5 结束语

本文为解决工况变化导致深度学习诊断方法性能衰退问题，提出一种深度流形迁移学习方法，更好地保持不同工况下振动数据分布的流形结构不变，从而赋予深度学习诊断方法对工况的鲁棒性并有效提高诊断精度。此外，本方法在训练过程只需故障样本，无需标签等其他任何信息，具有良好的适用性。将其应用于轴承及齿轮部件的变工况故障诊断任务，取得了比当前主流的深度学习及迁移学习方法更为优越的诊断性能。为实际旋转机械故障诊断提供了一个有效的理论工具。