考虑直觉模糊的多指标人岗双边匹配决策方法

李 松，袁安琪

1.河北大学 管理学院，河北 保定 071002

2.江西陶瓷工艺美术职业技术学院 经济管理学院，江西 景德镇 333000

双边匹配决策的目的是使匹配双方最大化找到满意的对方，是决策领域中的一个重要研究方向。近些年，针对不同背景下的双边匹配问题的研究取得了丰硕的研究成果，如人岗匹配问题[1]、供应链产销合作问题[2]、知识供需匹配问题[3]、房子交易与租赁问题[4]、风险投资匹配问题[5]、买卖交易匹配问题[6]、志愿者与应急任务匹配问题[7]、项目外包供需匹配问题[8]、考虑匹配稳定性的多属性双边匹配决策方法[9]等。目前双边匹配决策信息已不仅仅是单一的偏好排序信息，更多的是多指标评价决策信息。基于不同现实情境的多指标双边匹配决策问题的研究具有较强的现实意义，已经成为学者们关注的重点[10-11]。

现有解决各种偏好信息下的双边匹配问题给出了多种方法。但由于受现实双边匹配问题的复杂性和模糊性、双方主体认知的局限性等因素的影响，双方主体给出的可能是直觉模糊偏好信息[12]，因此学者们提出了基于直觉模糊数信息的双边匹配决策方法，将直觉模糊集矩阵转化为满意度矩阵构建多目标优化模型。目前直觉模糊集理论已应用于双边匹配决策领域[13-14]。直觉模糊偏好不仅能表达偏序关系，而且能够区分匹配主体的偏好强度[15]。近年来，直觉模糊偏好信息下的双边匹配问题引起了学者们的关注[16-21]。林杨依据最小对数二乘法构建了基于直觉模糊偏好关系的稳定双边匹配优化模型[16]；乐琦较早研究了直觉模糊偏好信息下的双边匹配问题，提出了一种直觉模糊偏好信息下的双边匹配方法[17]，在此基础上又分别提出了考虑双边主体的匹配意愿和直觉模糊偏好信息下基于得分函数的匹配满意度匹配优化模型[12，18]，基于新的排序函数提出一种考虑匹配意愿的双边匹配决策方法[19]，将文献[12，18]的方法拓展至区间直觉模糊偏好的情形[20]。张笛针对偏好序值难以区分匹配主体偏好强度的缺陷问题，依据TODIM法计算建立了一种双边公平满意匹配优化模型[21]。

在实际应用中，已有基于直觉模糊数偏好信息的双边匹配决策方法有很大的局限性，只有在双方主体的偏好信息都是以直觉模糊集的形式给出时，才能得以较好应用，如男女婚配、供应商匹配、风险投匹配以及一些人岗匹配等。在多种类型评价信息的多指标双边匹配决策问题中，由于直觉模糊数评价相对困难，因此应用直觉模糊偏好信息方法的研究成果很少。为使匹配结果更具合理性，本文考虑决策环境的复杂性和思维的模糊性，从匹配意愿的视角提出了一种基于直觉模糊的多指标人岗双边匹配决策方法。

1 预备知识与问题描述

1.1 直觉模糊数

定义1[13]设X为非空集合，则称E={x,μE(x),vE(x)|x∈X}为直觉模糊集，其中μE(x),vE(x)分别为X中元素x隶属于非空集合E的隶属度和非隶属度，且满足μE(x):X→[0,1],x∈X→μE(x)∈[0,1],vE(x):X→[0,1],x∈X→vE(x)∈[0,1],0≤μE(x),vE(x)≤1,x∈X。

此外，πE(x)=1-μE(x)-vE(x),x∈X表示集合X中元素x属于E的不确定度或犹豫度。此时，称α=(μα,vα)为直觉模糊数，其中μα∈[0,1],vα∈[0,1],μα+vα≤1。为方便，记Ⓗ为全体直觉模糊数的集，α+=(1,0)为最大直觉模糊数，α-=(0,1)为最小直觉模糊数。

定义2[22]给定任意直觉模糊数α=(μα,vα)，则得分函数s(α)=μα-vα，其中s(α)为α的得分值，且s(α)∈[-1,1]。

1.2 问题描述

设人岗双边匹配决策的主体分别为岗位和求职者，岗位A={ A1,A2,…,Am}，其中Ai是A中第i个个体，i=1,2,…,m；求职者B={B1,B2,…,Bn}，Bj是B中第j个个体，j=1,2,…,n。根据岗位的需要对求职者提出满意度评价指标为C={C1,C2,…,Ck1,Ck1+1,Ck1+2,…,Ck2,…,Ck3+1,Ck3+2,…,Ck4},Cb表示第b个评价指标，b=1,2,…,k1,k1+1,…,k4,C的评价指标权重向量为w＇=(w1＇,w2＇,…,w＇

k4)，wb＇表示指标Eb的权重，0≤wb＇≤1，为0-1特征信息型指标，Cp表示p第0-1个特征信息型指标，p=1,2,…,k1；C2={Ck1+1,Ck1+2,…,Ck2}为区间数信息型指标，Cq表示第q个区间数信息型指标，q=k1+1,k1+2,…,k2；C3={Ck2+1,Ck2+2,…,Ck3}为三角模糊数语言评价信息型指标，Cl表示第l个区间数信息型指标，l=k2+1,k2+2,…,k3；C4={Ck3+1,Ck3+2,…,Ck4}为直觉模糊数语言评价信息型指标，Ct表示第t个语言评价信息型的指标，t=k3+1,k3+2,…,k4。

定义vbij为岗位Ai在指标Cb下对求职者Bj的匹配满意度评价信息，求职者评价信息集分别对应0-1判断信息、区间数数值、三角模糊数形式和直觉模糊数形式，则vbij可表示为：

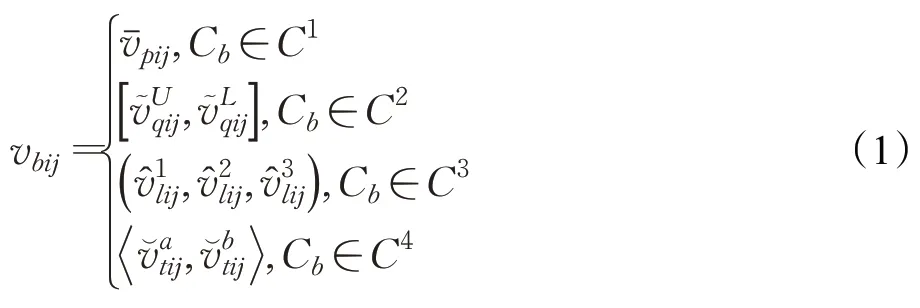
同理，求职者B对岗位A的匹配满意度评价指标集I={ I1,I2,…,If}，Ih为第h个评价指标，h=1,2,…,f，对应于Ih的指标权重向量为w″=(w1＇＇,w＇

2＇,…,w＇

f＇)，其中w＇＇h表示Ih的权重，0≤w＇＇

h≤1,。Ih可以是0-1特征指标、区间数或语言评价指标中的一种或几种。

多种形式评价信息的双边匹配决策问题，可使用三角模糊数和直觉模糊数方法对语言评价信息进行处理，通过计算理想点和实际评价水平之间的距离定义匹配满意度，进而得到了考虑多种形式评价信息的匹配主体双方的匹配满意度。

2 双边匹配方法

2.1 信息集结和满意度计算

考虑使用理想点来表示匹配主体岗位A对另一方匹配主体求职者B的最理想匹配满意度信息，设理想点为，针对指标评价值信息具有不同类型，给出规范化后的指标值实际水平与理想点之间的距离。定义vbij与v+的距离d(vbij,v+)为：

（3）若vbij为三角模糊数，则：

计算在各指标下岗位Ai对求职者Bj的评价信息与理想点之间的距离，得矩阵D=(Dij)n×m，其中Dij的计算公式为：

同理，计算在评价指标Ih下求职者Bj对岗位Ai的评价信息与正理想点之间的距离，可得求职者Bj对岗位Ai的匹配满意度βij。

2.2 决策模型构建和求解

2.2.1 模型建立

根据岗位A对求职者B的匹配满意度以及求职者B对岗位A的匹配满意度分析，引入变量xij，构建使双方匹配主体满意度都达到最大的多目标优化决策模型。即：

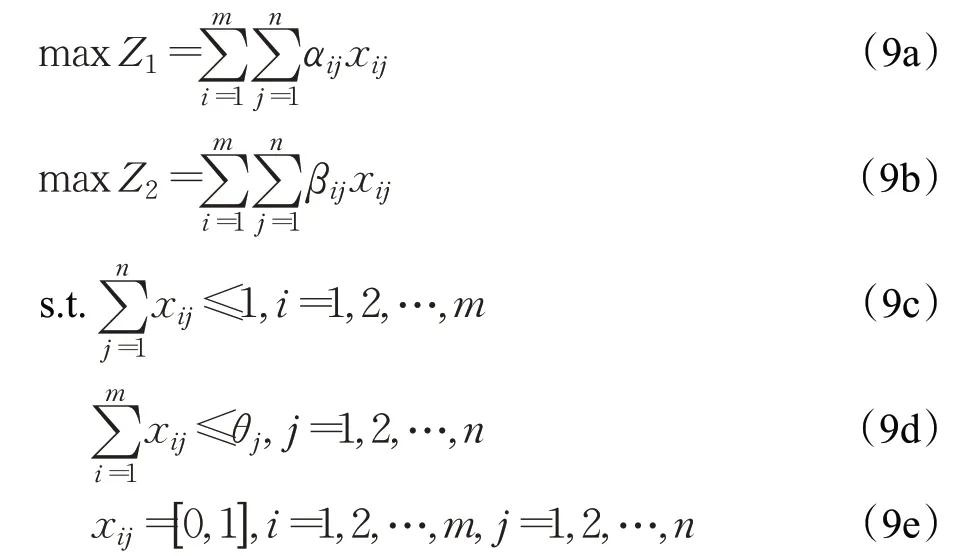
在式（9）中，式（9a）和式（9b）是目标函数，其中式（9a）的含义是使岗位A对B在所有评价指标下的满意度尽可能大；式（9b）的含义是使求职者B对A在设定的评价指标下满意度也尽可能大；式（9c）为求职者Bj至多被匹配到一个岗位的约束条件；（9d）表示θj为岗位招聘限定的最大人数的约束条件；式（9e）中xij=0表示岗位Ai对求职者Bj不能进行匹配，而xij=1表示岗位Ai对求职者Bj可以进行匹配。

2.2.2 模型求解

双边匹配优化模型一般采用线性加权和隶属函数加权等方法转化为单目标规划模型求解。线性加权法求解模型（9），即将式（9a）和式（9b）转化为式（10），然后采用LINGO等方法求解该模型。

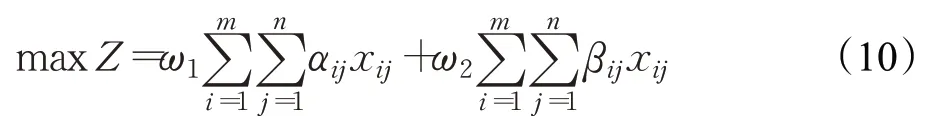
由于量纲可能不同，为求解模型（9）可采用基于隶属函数的加权方法。设Zmax1、Zmin1、Zmax2和Zmin2分别为Z1和Z2在束约条件（9c）～（9e）下的最大值和最小值，则Z1和Z2的隶属函数μZ1和μZ2可定义为：

设ω1和ω2分别表示μZ1和μZ2的权重，0≥ω1,ω2≤1,ω1+ω2=1,考虑公平性，可设ω1=ω2=0.5。通过简单加权将模型（9）转化单目标优化模型：

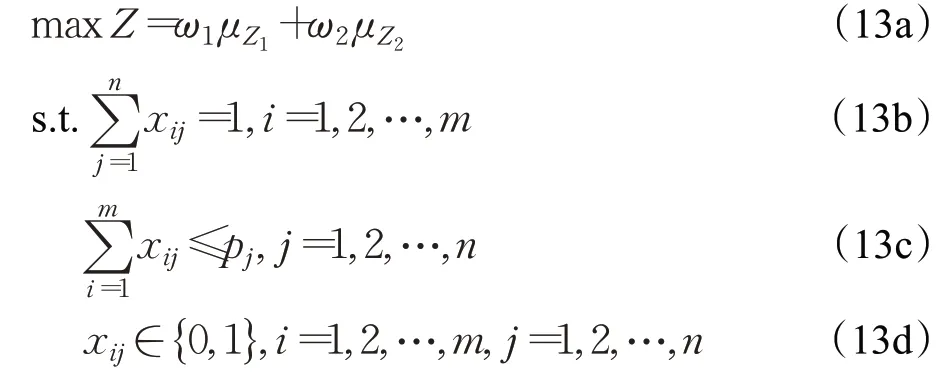
模型（13）可采用LINGO等软件进行求解获得双边匹配方案，也可采用启发式方法或智能优化算法进行求解。

3 算例分析

3.1 算例情境设定

某公司拟在4个岗位{ A1,A2,A3,A4}招聘员工，经过初筛确定6个求职者{B1,B2,…,B6}进入最终考核环节。岗位对求职者的匹配满意度测评主要考虑团队合作(C1)、沟通表达(C2)、期望薪酬(C3)、身体素质(C4)、工作经验(C5)、专业知识(C6)、英语与计算机水平(C7)和岗位适应性(C8)等指标。其中C5为0-1判断信息型指标；C3为区间数信息指标；C1、C2、C4、C6和C7为三角模糊数语言评价信息型指标，并使用T=6的语言评价集描述该类指标；C8为直觉模糊数语言评价信息型指标，该指标由专家小组根据{C1,C2,C4,C5,C6,C7} 6个指标，权重分别为：0.20、0.25、0.15、0.15、0.15、0.10，以直觉模糊数形式给出岗位对求职者综合满意度测评。并根据岗位实际，利用AHP法，给出岗位对求职者在各项指标上的权重。评价信息和权重如表1和表2所示。

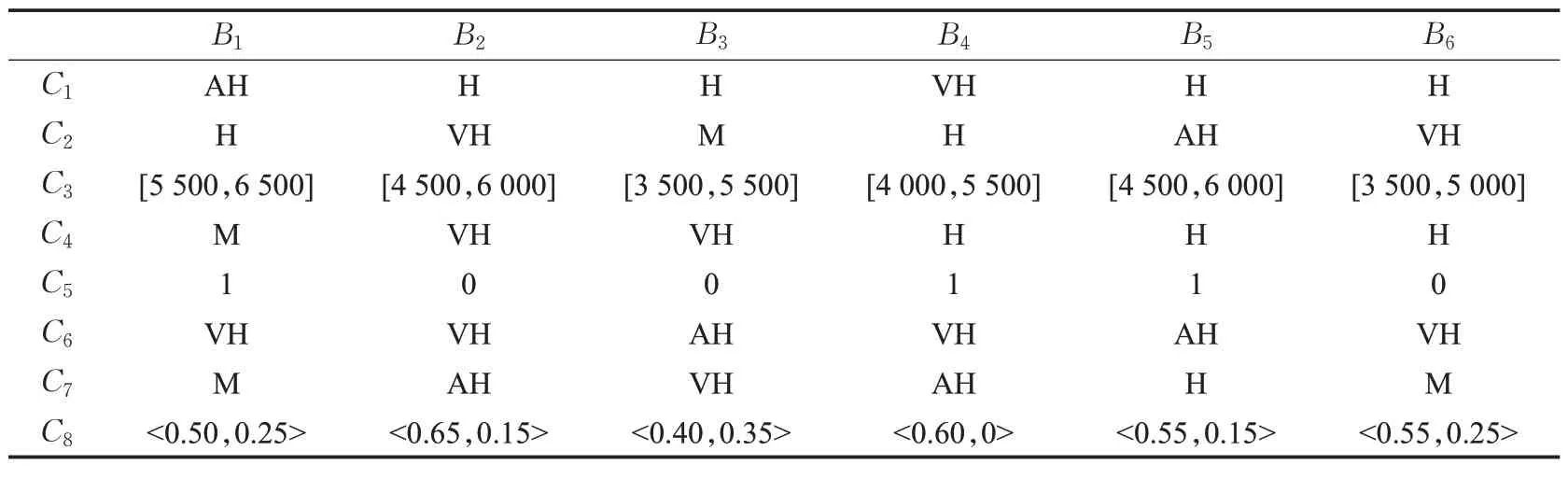
表1 岗位对求职者在各项指标上的评价信息Table 1 Assessment information given by company positions to employees on various indicators

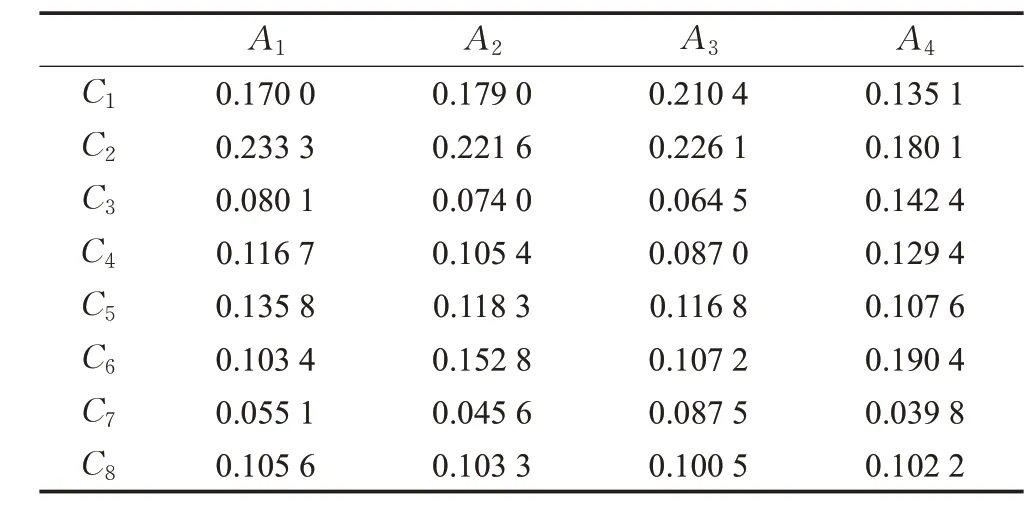
表2 岗位对各项指标给出的权重Table 2 Weight given by position to each indicator

求职者则根据自身的要求对4个岗位进行满意度评价，评价指标为：薪酬与福利(I1)、发展空间(I2)、休息休假(I3)和工作环境(I4)，专家通过访谈和问卷调查，给出求职者对各指标的权重。评价信息和权重如表3和表4所示。

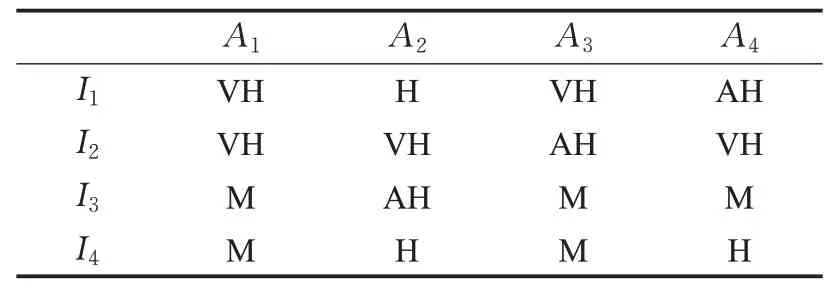
表3 各岗位在不同指标上的实际状态Table 3 Real information given by company positions on different metrics

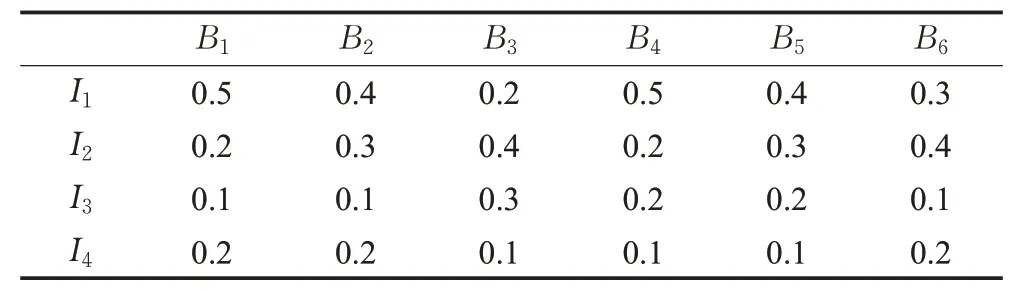
表4 各求职者对不同指标给出的权重Table 4 Weight given to different indicators by employees

3.2 计算结果及分析

利用评价指标处理方法，将语言评价信息进行数值转化，对区间型指标进行归一化处理；依据式（2）～（5）计算求职者到理想点的距离，并由式（7）和式（8）计算满意度，形成满意度矩阵[αij]4×6，如表5所示。同理可得求职者对岗位的满意度矩阵[βij]4×6，如表6所示。

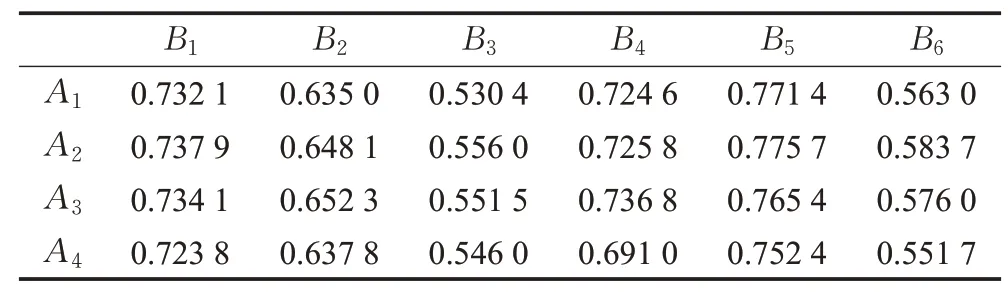
表5 岗位对求职者的满意度Table 5 Matching satisfaction degree given by company positions to employees

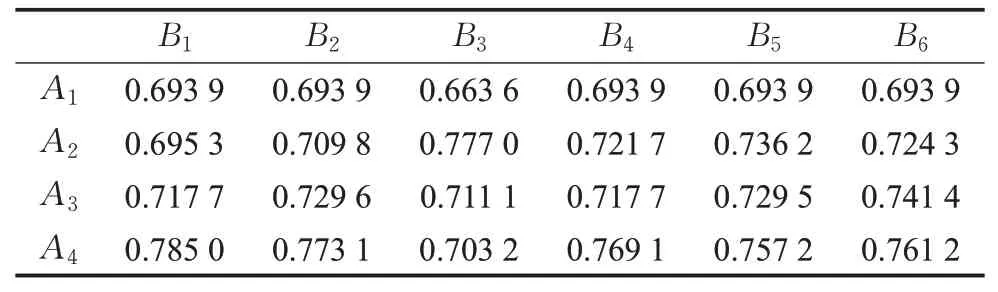
表6 求职者对岗位的满意度Table 6 Matching satisfaction degree given by employees to company positions

通过求解Z1和Z2的最值，可得Z1max=2.883 9，Z1min=2.445 5，Z2max=2.997 3，Z2min=2.810 1。设目标μZ1和μZ2的权重ω1=ω2=0.5，则将Z1max、Z1min、Z2max和Z2min代入模型（13a）中，得：

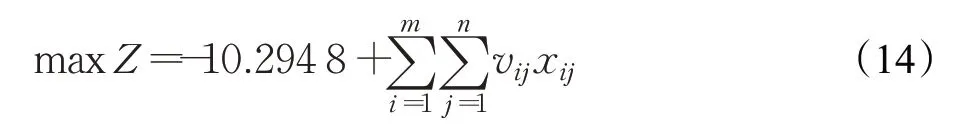
式中，V=[vij]4×6为系数矩阵，如表7所示。

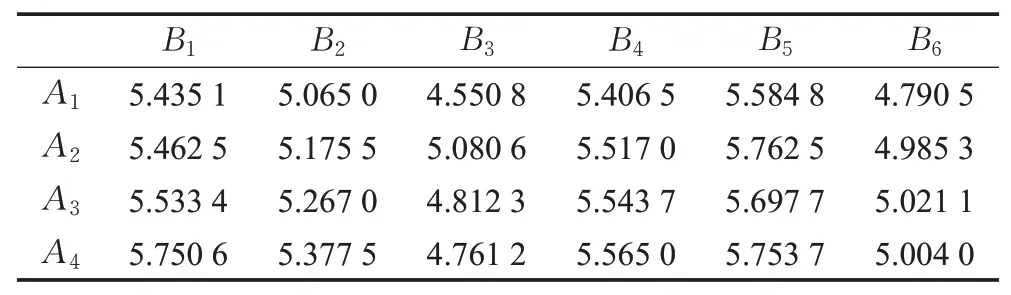
表7 系数矩阵Table 7 Coefficient matrix

采用优化软件包LINGO11.0软件求解，计算结果如下：

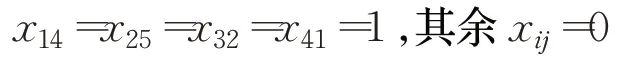
即岗位A1与求职者B4匹配，岗位A2与求职者B5匹配，岗位A3与求职者B2匹配，岗位A4与求职者B1匹配，求职者B3和B6未匹配。

为验证文中所提方法的可靠性，对模型（9）进行线性加权方法求解，从结果可以发现，隶属函数加权方法和线性加权方法的计算结果完全一致，这是因为在对各指标的评价信息进行数值转化时已经进行了数据归一化处理。说明文中所提方法的有效且可行；同时也说明在双边匹配决策过程中，如果事先对评价信息做过数据归一化处理，可不采用隶属函数加权方法求解，毕竟隶属函数加权方法求解Z1和Z2时的单目标最值比较麻烦。

4 结论

针对多指标人岗双边匹配决策环境，将直觉模糊数评价信息引入到多指标人岗双边匹配决策过程，充分考虑了决策环境的复杂性和思维的模糊性，通过专家给出求职者在岗位适应性指标上的直觉模糊评价信息，提出了基于模糊直觉多指标人岗双边匹配决策方法，采用属函数加权法求解模型，获得双边匹配方案。并通过一个人岗双边匹配问题的案例证明了该方法的的可操作性和实用性，通过算例可知，该方法具有一定的优越性，可为人岗双边匹配问题提供一种新算法。本文对多指标人岗双边匹配决策方法没有设定求职者对岗位的直觉模糊数评价指标。其原因一是为简化计算，二是实际求职者对岗位的了解程度一般都比较高，不需要设定直觉模糊评价信息指标，但这并不影响本文提出的人岗双边决策方法的应用。