基于权邻域的代表性用户抽样算法

何水苗，班志杰

内蒙古大学 计算机学院 内蒙古自治区社会计算与数据处理重点实验室，呼和浩特 010020

社交网络是指用户以及用户之间交互所组成的一个复杂网络。它在信息传播、想法分享和相互影响方面发挥着至关重要的作用。其中的一部分用户在社会网络影响中扮演着重要的角色[1-4]。例如产品推荐，一些用户的关注点可以反映出整体用户的兴趣爱好，这对于市场营销[5]是有帮助的。那么代表性用户抽样问题就是在大规模社交网络中抽取一个用户子集，使其可以统计代表整个网络中所有用户的特点。

目前，一些学者对于用户抽样问题进行相关研究，但不同任务下的用户抽样有着不同的定义。影响力最大化[6]是指利用一部分用户子集来扩大影响力的传播范围。寻找意见领袖[7]是指社交网络中一部分用户发表的观点能够影响其他人做决定。代表性用户抽样[8]是指要寻找一些用户，他们可以统计代表网络中所有用户的特点。当前对于代表性用户抽样问题的研究工作比较少。文献[9]首次提出抽取代表性子集的问题，探究如何在一个复杂网络中抽取代表性样本。文献[10]提出了一种基于扩展图的网络社区抽样方法，该方法通过定义目标函数来表征代表性子集在拓扑结构的覆盖范围。文献[11]又进一步提出在网络中抽取一些带有偏见节点的必要性。文献[12]提出了一个通用框架来抽取代表性子图，并使用随机游走算法进行代表性子图抽样。文献[13]提出一种基于K-NN图的代表性子集抽取方法。但这些研究都是基于静态网路的，文献[14]重点研究了在动态社交网络中抽取代表性子集问题，利用用户邻域收集的信息来探索社交网络的结构。然而这些抽样方法在抽取代表性子集时都只考虑了网络的拓扑结构[15]，忽视了用户属性所包含的信息。文献[16]提出的骨架学习方法是从信息传播的角度进行代表性用户抽取，它主要是通过贝叶斯推断将每个节点连接到一个代表性节点。文献[17]正式定义了代表性用户抽样问题，并且证明了该问题属于NP-hard问题。他们提出的统计分层抽样模型，虽然考虑了用户之间的关系，但没有充分研究的网络拓扑结构。

由于在网络的拓扑结构中也蕴含着用户大量有价值的信息，所以为了从拓扑结构中获取用户包含的丰富内容，采用权邻域对网络的拓扑结构进行描述，并利用拓扑结构和用户属性进行代表性用户的抽取，最后通过实验进一步检验了所提出算法的有效性。

1 基于权邻域的代表用户抽样算法

1.1 问题描述

G(V,E)表示社交网络，其中V表示用户集合，E表示用户之间边的集合， ||V=N表示图上共有N个用户，T⊆V表示抽取的代表性用户集合， ||T=K表示抽取的代表性用户个数。本文的工作就是对于给定的社会网络G(V,E)，抽取一个用户子集T(T⊆V, ||T=K)，使得提取的用户子集尽可能地统计代表整个网络中所有用户。他们并不仅仅限制于具有较强影响力的个体或者是对于观点传播具有很强领导力的用户。这里所说的代表性用户，从属性特征角度而言，他们能够很好地代表原数据集用户的属性特征。从分布特征角度而言，代表性子集应尽可能拟合原数据集的样本分布，即与原数据集具有较少的分布损耗，代表性子集能够拟合原数据集每个领域的人物分布。

为了更好地阐述代表性用户抽样这个问题，通过一个例子来说明。如图1，这是一个基于人工智能和云计算的合著网络。从图中可以看到每个学者对于不同研究领域的感兴趣程度，其中左边表示研究者对人工智能研究领域的感兴趣程度，右边表示研究者对云计算研究领域的感兴趣程度，二者之和为1，学者之间的边权重表示学者之间合著的论文数目。例如，从图中可以看出学者B相比于对人工智能研究领域的感兴趣程度（0.1），他在云计算研究领域的兴趣程度比较高（0.9），由此看出他在人工智能研究领域具有更高的代表性；而学者H相比于云计算研究领域的感兴趣程度（0.1），他在人工智能研究领域更感兴趣（0.9），说明学者H在人工智能研究领域更具有代表性。由此可见，在不同的研究领域中，抽取的代表性用户是不同的，所以研究的目标是抽取一个代表性用户子集，使得它能够统计代表整个网络中所有用户的属性特征。

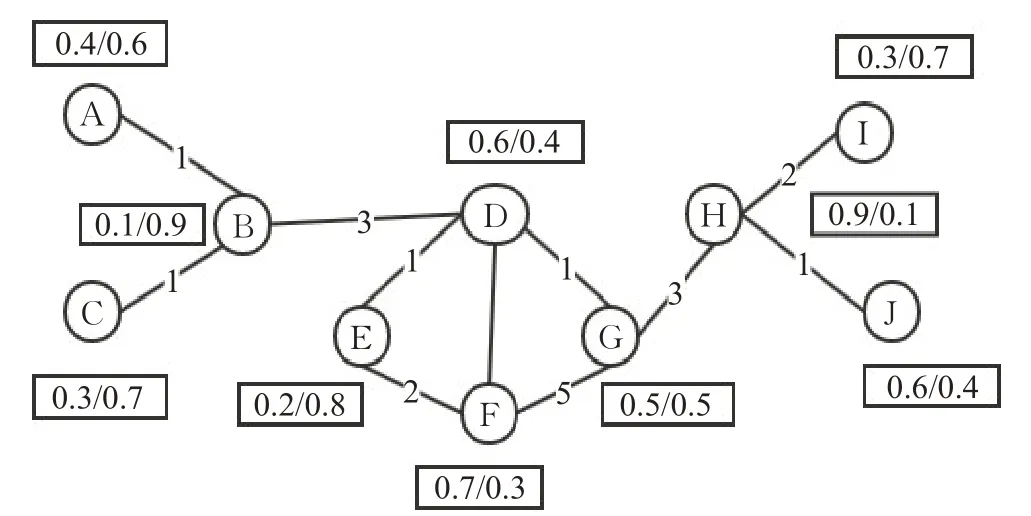
图1 多属性合著网络Fig.1 Multi-attribute coauthor network

文献[17]提出的统计分层抽样模型，首先将所有用户根据属性值分成不同的属性组；接着在每一个属性组中，通过计算用户的代表度之和得到属性组代表度；最后将用户的所有属性组代表度累加起来，利用质量函数进行数值化评估，每次选取增量值最大的用户作为代表性用户。由于该模型在计算用户代表度的过程中，对网络的拓扑结构没有进行更深入的研究，从而忽略了在拓扑结构中蕴含的用户有用信息，所以本文对统计分层抽样模型进行改进。通过利用权邻域对图的拓扑结构进行充分描述，从而获得用户包含的更多有价值信息，将权邻域和用户属性结合起来抽取代表性用户。

1.2 权邻域

在衡量一个节点重要性时，不仅考虑节点本身的度，而且联合它与邻居的权重以及邻居节点的度。假设两个节点具有相同的度，若其中一个节点的邻居节点影响力比较大，那么该节点也将具有更高的影响力。另外，在大多数的加权网络中，每条边在网络结构和功能中具有不同的意义。例如，在合著网络中，一个作者权邻域值越大，表明该作者和邻居合著的论文比较多，那么成为代表性用户的可能性越大，权邻域的计算公式如下：

其中，di表示节点i的度，wij表示节点i和节点j之间的权，dj表示节点j的度，Γ(i)表示节点i的所有邻居。

为了选取不同规模社交网络中的代表用户，需要进行归一化处理。通过将所有边两端节点度的乘积相加之和与所有边所占的比重进行归一化，用φi＇表示，如下式所示：

其中，di和dj表示节点i和节点j的度，w表示节点之间构成的边。由于数据集的大小以及数据集不同的取值等因素，所以设置一个阻尼系数η来增加算法的可靠性，它的取值范围为（0，1]。

如图2所示。如果单纯从节点连接的度数角度来识别有代表性的用户，那么有些隐藏的重要节点就无法识别。例如节点1的度数为3，而节点2和节点3的度数均为5，这样看起来好像节点1没有节点2和节点3重要，但是节点1处于图中的关键位置，它是节点2和节点3的沟通桥梁。这里的节点1就是隐藏的重要节点。那么，通过采用权邻域计算方法，可以得到每个节点的权邻域值，这里给出前三个节点的权邻域值排名，即节点1为3.68、节点2为2.5、节点3为2.21。由此可以看出节点1最重要，因为节点1所处的位置比较核心，虽然它的度数不是最大的，但是它周围的邻居节点比较重要。在现实生活中，一个比较有影响的用户，一般他周围的朋友大多数都比较重要的。例如在一个研究邻域中，比较有权威性的专家一般和影响力比较大的学者合著文章。同样，仅从度数角度识别节点的代表性，有些度数相同节点的重要性便无法识别，如图中节点2和节点3的度数一样。但是采用提出的权邻域计算方法可以发现，节点2的代表性高于节点3，因为节点2的邻居节点相比较于节点3的邻居节点更重要一些，所以节点2比节点3更具有代表性。

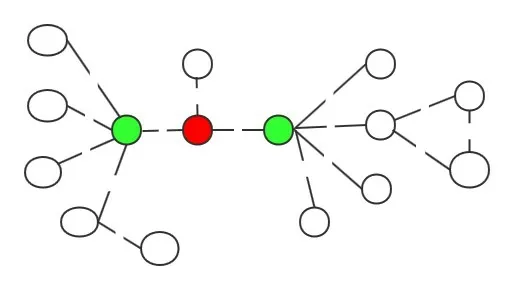
图2 权邻域举例Fig.2 Example of weighted neighborhood

1.3 相关定义

为了研究方便，给出与本文算法相关的公式定义。定义1用户代表度

用户vi在属性值ajl上对vi＇的代表度，称之为用户代表度，用B(vi,vi＇,ajl)表示。它的计算公式为用户vi在属性aj上的属性值ajl占该用户所有属性和∑asl的比重与其权邻域φi＇的乘积，公式如下：

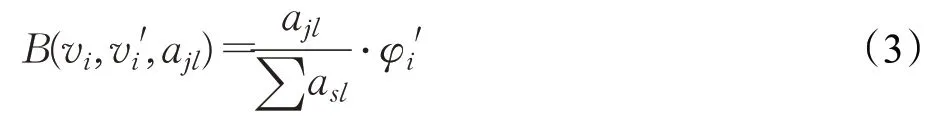
其中，对于任意一个用户vi,ajl表示用户vi在属性aj上的属性值，∑asl表示用户vi在所有属性上的属性值之和，vi＇表示用户vi的邻居，φi＇表示用户vi的权邻域值。

定义2属性组

分层抽样是将总体按照规定的比例从不同层中随机抽取个体，由于这种方法抽到的样本代表性比较好，抽样误差比较小，所以基于这个想法，将用户按照属性值划分成不同的属性组。通过定义一组个体Vl⊆V，其对应的属性值为ajl，将这样的一组个体与相应的属性作为一个属性组，用A表示所有组的集合，公式如下。其中，s表示属性组的数目。

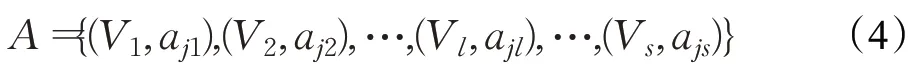
定义3属性组代表度

对于一个属性组(Vl,ajl)(1≤l≤s)，属性组代表度表示子集T在属性ajl上代表Vl中的所有人。通过计算用户vi在该属性组下用户代表度的和，得到该属性组的代表度，用P(T,l,ajl)表示，公式如下。其中，T表示对于该属性组具有代表性的用户子集。

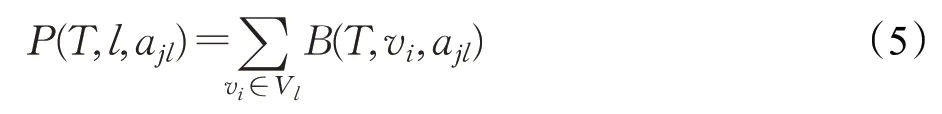
定义4质量函数

目标是找到一个代表性集合，使得它对于所有属性都具有最高的属性组代表度，所以通过将用户vi的所有属性组代表度P(T,l,ajl)加起来，利用质量函数Q(G,X,A,T)对其进行数值化评估，公式如下：

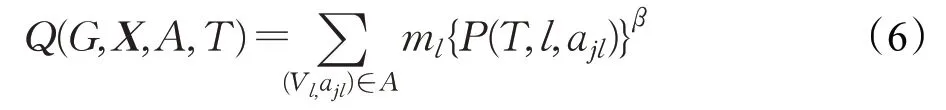
其中，质量函数Q(G,X,A,T)中的G表示输入的社交网络，X表示属性矩阵，A表示属性组，T表示抽取的代表性用户集合。参数ml表示每个属性组(Vl,ajl)∈A的重要程度，取值为Vl的平方根。若它的取值较高，则表示该属性组具有较好的代表性。参数β表示一种偏差，这种偏差是指通常会选择一些不太具有代表性的用户来增加全局代表性，它的取值范围在（0，1]。

1.4 算法描述

目标是抽取一个代表性用户子集，它能够代表整个网络中所有用户的特点。因此，为了使得抽取的用户更具有代表性，在统计分层抽样模型基础上对其进行改进。首先为了从网络的拓扑结构中获取用户更多有用的信息，利用权邻域对其进行描述；之后在计算用户代表度的时候，采用将权邻域与用户属性值相结合的方式进行用户代表度的计算；然后根据属性值将用户分成不同的属性组，计算用户的属性组代表度；接着把用户所有属性组代表度的增量累加起来，通过质量函数对其进行数值化评估；最后采用启发式贪婪算法进行代表性用户的抽取。按照上述方法以此类推，每次抽取增量值最大的用户作为代表性用户，直到选取足够数量的代表性用户为止，算法结束。代码如下所示：

输入：用户集合V，属性集合M，属性个数X，用户代表度B，抽取代表性用户集合个数K。

输出：代表性用户集合T。

接下来，对本文提出的算法进行复杂性分析。每次遍历所有的用户并找到使得质量函数Q增量值最大的用户作为代表性用户，直到选取K个代表性用户为止。在抽取代表性用户的过程中，首先判断代表性用户集合中用户个数是否小于K，如果满足条件，则为变量赋初值；接着遍历所有用户来寻找使得质量函数Q增量值最大的用户，并计算该用户的属性组代表度。其中，属性组数量最大为t。然后在每个属性组中，计算该用户的用户代表度。因此该算法整个过程所需要的时间复杂度为O(t×K× ||E)，空间复杂度为O(1)。这里的K表示抽取的代表性用户数量，t表示属性组的数量， ||E表示节点之间边的数量。

其中，代码第6～10行计算用户在任意一个属性组中的用户代表度之和；代码第5～12行计算用户的所有属性组代表度增量；代码第13行计算通过增加用户之后的质量函数的增量；代码第14～17行判断用户的增量是否大于当前最大值增量，若大于当前最大值增量，就将用户放入索引中，并更新相关参数；接着继续遍历下一个用户，直到遍历足够数量的代表用户，算法结束。

2 实验

2.1 实验环境

本文实验所使用的计算机基本配置为Intel®Celeron®CPU N2930@1.83 GHz，4.00 GB内存，操作系统为Windows7，开发工具为CodeBlocks 17.12，使用C++语言进行编程。

2.2 数据集

本文一共选择了四个数据集进行验证，分别是ICWSM数据集、WSDM数据集、Database数据集[17]和Datamining数据集[17]。各个数据集如表1所示。

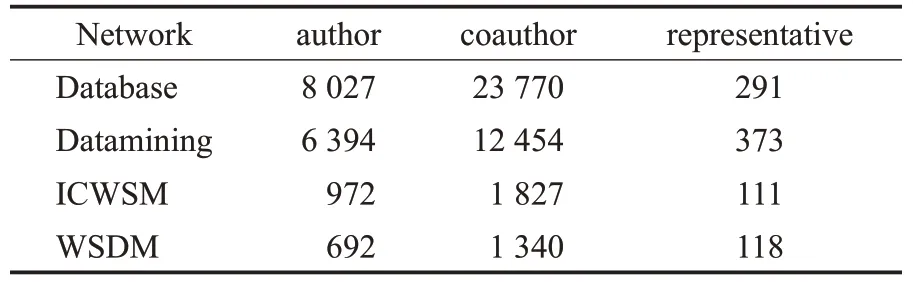
表1 各数据集统计Table 1 Statistics of each data set

ICWSM数据集和WSDM数据集分别收集了2015—2017年期间会议上发表的论文。对于作者属性的提取，一共收集了50个作者发表论文的关键字作为作者属性，同时将作者使用关键字的次数作为属性值。其中，ICWSM数据集包含972个用户和1 827个用户之间的合著关系；WSDM数据集包含了692个用户和1 340个用户之间的合著关系。另外，由于一个会议的程序委员会一般是该领域的专家，所以通过将程序委员会中没有合著关系的作者删除，最终在这两个数据集上分别选取2015—2017年间的111个和118个程序委员会成员作为标准代表性用户集合。

为了验证本文提出算法的有效性，又在两个公开的数据集上进一步验证。其中，Database数据集和Datamining数据集分别收集了2007—2009年发表在（SIGMOD、VLDB、ICDE）和（SIGKDD、ICDM、CIKM）上的论文。Database数据集包含8 027个用户和23 770个用户之间的合著关系；Datamining数据集包含了6 394个用户和12 454个用户之间的合著关系。在这两个数据集上选取了在2007—2009年间的程序委员会作为标准代表性用户集合，分别收集了291个和373个代表性用户。

2.3 对比算法

使用度排序算法、PageRank算法、HITS算法、SSD算法和S3算法作为基线算法。

度排序[18]（Degree）算法。该算法是根据节点度的大小进行排序。

PageRank[19]算法。该算法的核心思想：若一个网页被很多网页链接，那么说明该网页相对较重要，它的PageRank值也会相对较高；若一个PageRank值很高的网页链接到其他的一个网页，那么这个网页的PageRank值也会相对比较高。其中，PR表示PageRank算法。

HITS[20]算法。该算法将网页分为两种，包括Hub页面和Authority页面。其中，Hub页面是指包含了很多指向高质量Authority页面链接的网页；Authority页面是指某个领域中网页内容的质量比较高，由很多高质量的Hub页面所指。其中，HITS_a和HITS_h分别表示HITS算法中以Authority和Hub为排序指标。

SSD和S3算法。它们分别表示文献[17]中的多策略抽样模型和统计分层抽样模型。其中，SSD模型是将所选代表性用户的多样性最大化，这里的多样性是指抽取的代表性用户尽可能覆盖多的属性组。S3模型在前文已详细阐述。按照原文献中设置的参数∂=0.6对其进行实验。

2.4 评价指标

采用精确率、召回率和F1-Measure来评价每个算法的性能。

精确率主要用来评价算法的查准率，本文抽取结果列表中排名前M个用户与标准代表用户集进行对比，若其中有S个用户位于标准代表用户集中，则准确率如下式所示：

召回率主要用来评价算法的查全率，本文抽取结果列表中前K个用户与标准代表用户集进行对比，若其中有S个用户位于标准代表用户集N中，则召回率如下式所示：

由于准确率与召回率两者存在一种互补关系，需要一个综合指标涵盖这两个指标，于是引出了F-Measure。它是准确率和召回率的加权调和平均，本实验采用F1-Measure作为评价指标，如下式所示：

2.5 实验与分析

2.5.1 计算复杂性

在一般情况下，一个网络中通常拥有成千上万个节点，希望最终抽取的代表性节点是高效且合理的。接下来对7种算法的计算复杂性进行分析，如表2所示。这里n表示所有用户，K表示抽取的代表性用户，t表示属性组数量， ||E表示节点之间边的数量，t(ε)表示迭代次数，ε表示阈值。

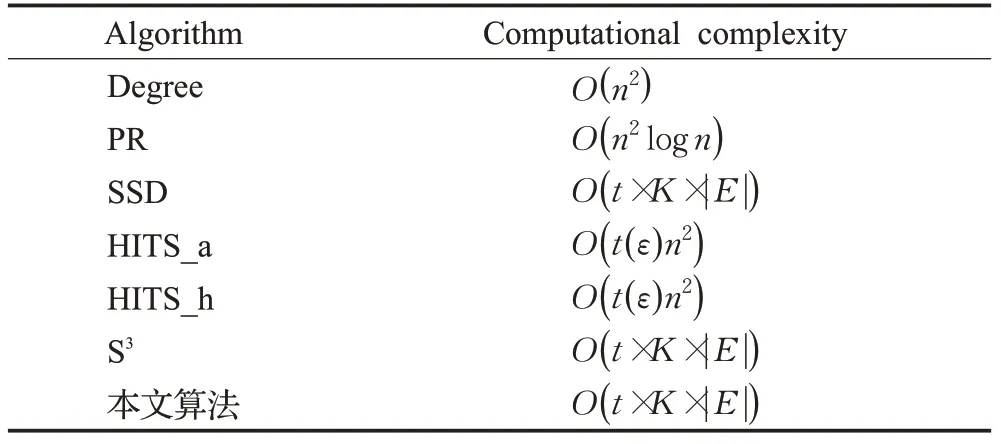
表2 不同算法的计算复杂性Table 2 Computational complexity of different algorithms

从表2中可以看到，不同的算法具有不同的计算复杂性。其中，Degree算法的计算复杂性最低。PR算法的计算复杂度为O(t(ε)n2)。这里的迭代次数t(ε)与收敛的阈值有关，对于大型网络，这个迭代次数t(ε)与边的关系是接近线性的logn，所以最终PR算法的复杂性为O(n2logn)。HITS_a算法和HITS_h算法的计算复杂性均为O(t(ε)n2)，它与迭代次数有关。本文算法与S3算法和SSD算法的计算复杂性一样，均为O(t×K× ||E)。S3算法在抽取代表性用户的过程中，需要考虑该用户与其邻居能够为属性组做多少贡献，直到抽取K个代表性用户为止。对于SSD模型，每次选择最贫穷的属性组，并选择一个用户来增加该属性组的代表程度，使得最终抽取的代表性用户尽可能覆盖多的属性组。虽然本文算法的计算复杂性不是最低的，但本文算法在与S3算法和SSD算法计算复杂性相等的情况下，抽取到的代表性用户更加准确。

2.5.2 参数影响

通过测试阻尼系数η和β的变化，分析其对本文算法的影响。其中，X轴表示参数β的取值，Y轴表示阻尼系数η的取值，Z轴是通过在Top10、Top35和Top75上抽取代表用户之后，采用平均值来衡量不同阻尼系数η和参数β下抽取代表用户的整体水平。各个数据集的参数影响如图3～图6所示。

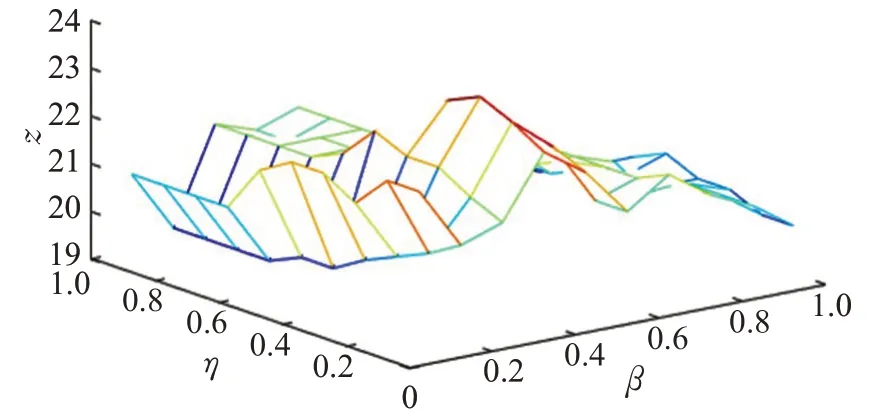
图3 Database数据集下参数的影响Fig.3 Influence of parameters on Database dataset

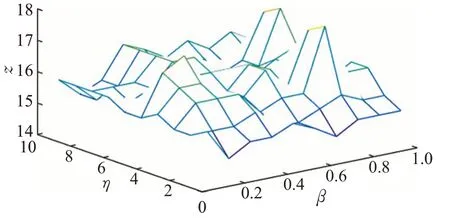
图6 WSDM数据集下参数的影响Fig.6 Influence of parameters on WSDM dataset

为了在不同采样率下都能够抽取到更具代表性的用户，通过反复实验，在不同的数据集上取得最终参数结果。从图3可以看出，在Database数据集上，参数β的取值范围为（0，1]；阻尼系数η的取值范围为（0，1]；Z轴的取值范围为（19，24）。最终通过反复实验，在Database数据集上参数β选取0.3，阻尼系数η选取0.5；从图4可以看出，在Datamining数据集上，参数β的取值范围为（0，1]；阻尼系数η的取值范围为（0，10]；Z轴取值范围为（22，27）。最终在Datamining数据集上参数β选取0.7，阻尼系数η选取3。从图5可以看出，在ICWSM数据集上，参数β的取值范围为（0，1]；阻尼系数η的取值范围为（0，1]；Z轴取值范围为（6.5，9）。最终在ICWSM数据集上参数β选取0.2，阻尼系数η选取0.5。从图6可以看出，在WSDM数据集上，参数β的取值范围为（0，1]；阻尼系数η的取值范围为（0，10]；Z轴取值范围为（14，18）。最终在WSDM数据集上参数β选取0.3，阻尼系数η选取2。接下来，通过在不同的数据集上按照上述选取的参数对本文的算法进行实验。

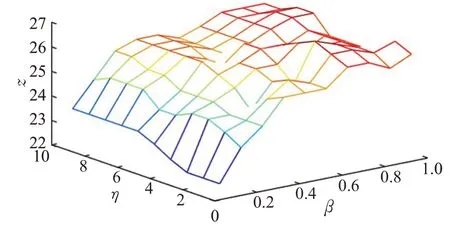
图4 Datamining数据集下参数的影响Fig.4 Influence of parameters on Datamining dataset

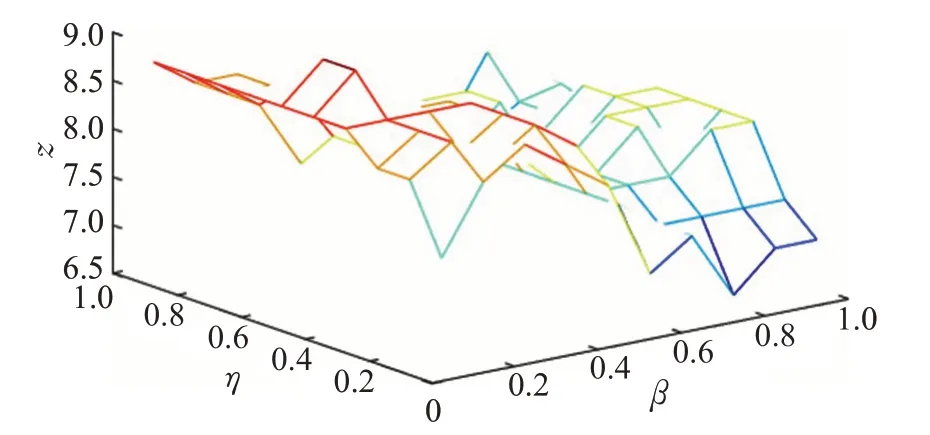
图5 ICWSM数据集下参数的影响Fig.5 Influence of parameters on ICWSM dataset

2.5.3 实验对比

本文通过在四个数据集上与Degree排序算法、PageRank算法、HITS_a算法、HITS_h算法、SSD算法和S3算法进行对比实验，本文算法在各种评价指标方面都有提升，表3～表6给出各个数据集的实验结果。

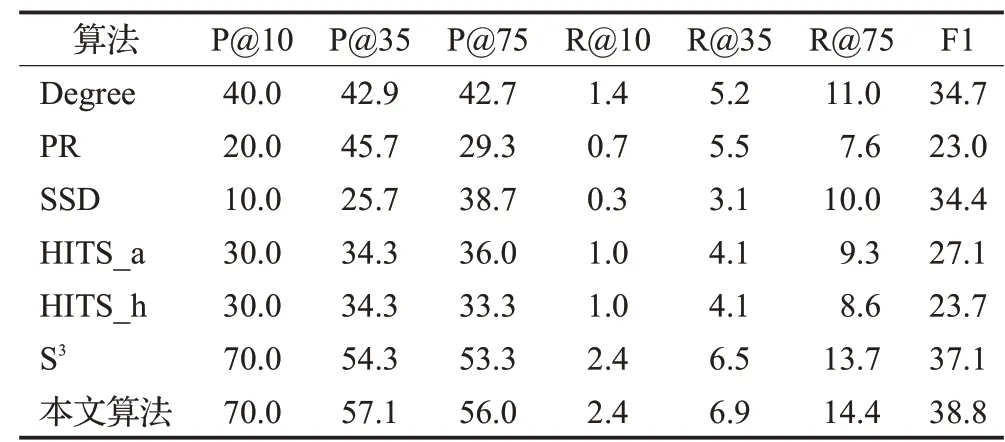
表3 在Database数据集上的实验结果Table 3 Experimental results on database dataset%

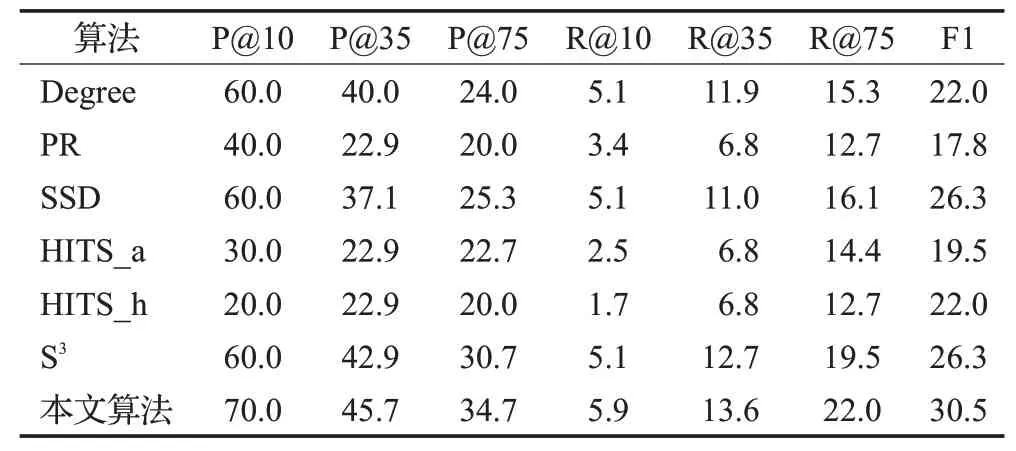
表6 在WSDM数据集上的实验结果Table 6 Experimental results on WSDM dataset %

在Database数据集上运行的实验结果如表3所示，虽然在抽取前10个用户中，本文算法与S3算法在精确率方面表现持平，但与其他算法相比有较大的提升，提升了30个百分点，提升率达到75%；在抽取前35个用户中，与所有算法相比，本文算法在精确率方面有2.8个百分点的提升，提升率达到了5.2%；在抽取前75个用户中，本文算法与所有算法相比，精确率有2.7个百分点的提升，提升率达到了5.1%。

由于在Database数据集中的标准代表用户数为291个，而抽取的代表用户仅为10～75个，故召回率相对较低。与所有算法相比，在抽取前35个用户和75个用户时，本文算法在召回率方面分别提高了0.4个百分点和0.7个百分点，提升率分别达到了6.2%和5.1%；虽然在抽取前10个用户中，本文算法与S3算法表现持平，但与其他算法相比有较大的提升，提升了1个百分点，提升率达到71.4%；与所有算法相比，本文算法在F1-Measure有1.7百分点的提升，提升率达到了4.6%。

在Datamining数据集上运行的实验结果如表4所示，当抽取前10个用户时，本文算法优于其他所有算法，在精确率方面有10个百分点的提升，提升率达到了12.5%。尤其在抽取前35个用户上，本文算法与S3算法相比有较高的提升，在精确率方面提高了8.5个百分点，提升率达到了13.5%；在抽取前75个用户上，与所有算法相比，本文算法在精确率方面提高了4个百分点，提升率达到了6.7%。

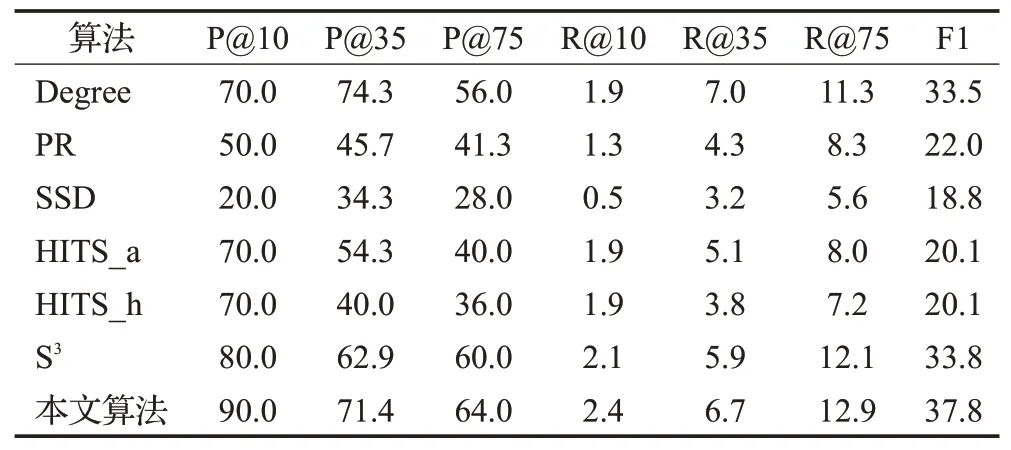
表4 在Datamining数据集上的实验结果Table 4 Experimental results on Datamining dataset%

由于在Datamining数据集有373个代表性用户，而抽取的用户仅为10～75个，所以召回率相对比较低。在抽取前10个用户中，与所有算法相比，本文算法有0.3个百分点的提升，提升率达到了14.3%；在抽取前35个用户中，与S3算法相比，本文算法提升了0.8个百分点，提升率达到了13.6%；在抽取75个用户中，本文算法与所有算法相比，提升了0.8个百分点，提升率达到了6.6%。在F1-Measure评价指标上，与所有算法相比，本文算法提升了4个百分点，提升率达到了11.8%。

在ICWSM数据集上运行的实验结果如表5所示，在抽取前10个用户中，本文算法在精确率、召回率评价指标上和S3算法持平，但优于其他算法，在精确率方面有10个百分点的提升，提升率达到了50%；与S3算法相比，本文算法在Top35上的精确率提高了2.9个百分点，提升率达到了14.5%，召回率提高了0.9个百分点，提升率达到了14.3%；尤其在Top75上，本文算法在精确率方面提高了5.3个百分点，提升率达到了33.1%，召回率提高了3.6%，提升率达到了33.3%；与所有算法相比，本文算法在F1-Measure提高了1.8个百分点，提升率达到了10%。

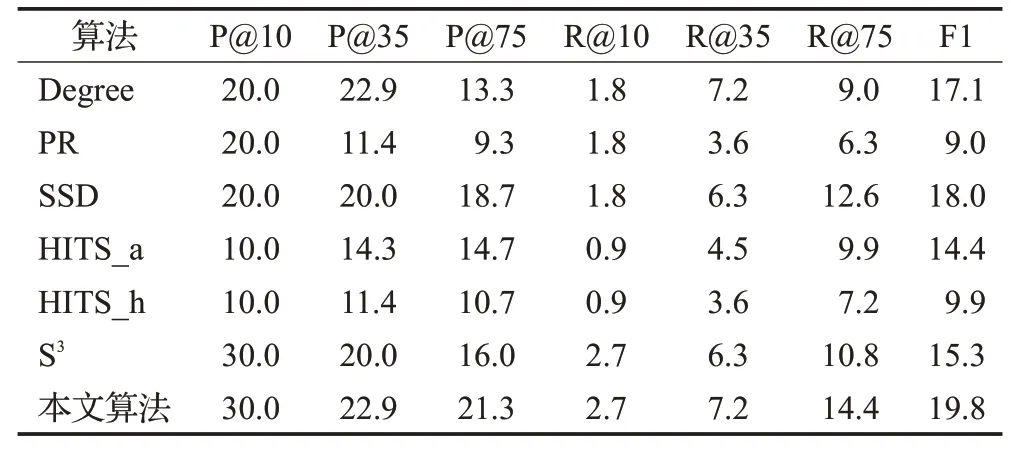
表5 在ICWSM数据集上的实验结果Table 5 Experimental results on ICWSM dataset %

在WSDM数据集上运行的实验结果如表6所示，在抽取前10个用户中，本文算法优于其他所有算法，在精确率上提高了10个百分点，提升率达到了16.7%，在召回率上提高了0.8个百分点，提升率达到了15.7%；在Top35上，与所有算法相比，本文算法在精确率方面提高了2.8个百分点，提升率达到了6.5%，召回率提高了0.9个百分点，提升率达到了7.1%；在Top75上，本文算法在精确率方面提高了4个百分点，提升率达到了13%，召回率提高了2.5个百分点，提升率达到了12.8%；与所有算法相比，本文算法在F1-Measure评价指标上提高了4.2个百分点，提升率达到了16%。

2.5.4 运行效率

本文通过计算算法的运行时间来评价算法效率，在实验中通过记录算法开始前的系统时间和算法结束后的系统时间，二者差值为算法的运行时间，算法的运行时间如表7所示。

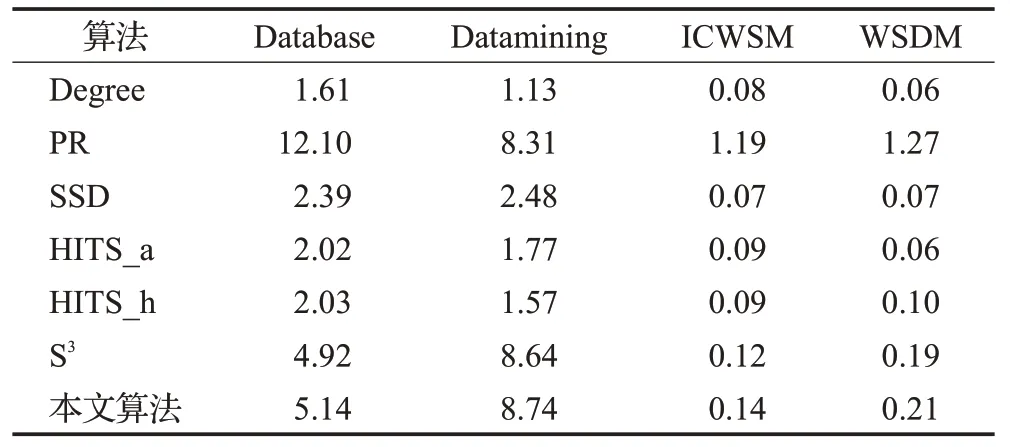
表7 不同算法的运行时间Table 7 Running time of different algorithms s

在Database数据集上，本文算法比S3算法用时长0.22 s，在Datamining数据集上本文算法比S3算法用时长0.1 s。在ICWSM数据集和WSDM数据集上本文算法比S3算法用时均长0.02 s；虽然本文算法除了比PageRank算法耗时少之外，相比于其他算法耗时都比较多，但在精确率、召回率和F1-Measure方面均有提升，从而使得抽取的代表性用户更加准确。

3 结束语

本文提出了基于权邻域的抽样算法来解决代表性用户抽样问题。为了使抽取的用户更具有代表性，本文在计算用户代表度时，不仅考虑了用户的属性，还融合了权邻域方法来提取拓扑结构中用户的丰富内容，最后采用启发式贪婪算法对代表性用户进行抽取。实验结果表明该算法的性能在不同的数据集上均有提升。下一步的工作将会在本文的基础上，对综合考虑拓扑结构的局部和全局来抽取代表性用户。