基于O-SVD与FSC的滚动轴承微弱故障特征提取研究*

张 震,刘保国,周万春,黄传金

(1.郑州工程技术学院 机电与车辆工程学院,河南 郑州 450000;2.河南工业大学 机械工程学院,河南 郑州 450001)

0 引 言

轴承在旋转机械中的应用极为广泛,但是由于其服役环境存在变载荷、大扰动、强冲击、高噪声等特点,因此极易发生故障,造成重大的经济损失,甚至是人员伤亡。

轴承早期故障的动态响应往往比较微弱,极易被噪声所淹没,因此,如何能够在低信噪比情况下,对其微弱故障特征进行提取,并保证其细节特征的完整性,成为了轴承故障诊断研究领域的一大难点。

AHMED S M等人[1]使用小波变换方法对轴承信号特征进行了提取,但是小波变换的效果与小波基的选择密切相关,个人经验将严重影响轴承信号特征提取的效果。

徐永成等人[2]使用改进的经验模态分解(empirical mode decomposition,EMD)算法,将轴承的故障信号与噪声信号进行了分离,取得了较好的效果;但使用EMD算法存在的模态混叠问题并未得到根本解决。王志武等人[3]采用局部均值分解和奇异差分谱法进行了轴承信号特征提取,该方法虽然提高了提取信号的信噪比,但是信号的细节特征方面并未受到特殊关注。刘兴教等人[4]基于峭度原则,对集合经验模态分解(ensemble empirical mode decomposition,EEMD)算法的有效本征模函数(intrinsic mode function,IMF)进行了选择,获得了较好效果;但是通过该方法提取到的信号的细节特征丢失较为严重。

奇异值分解作为一种零相位、零时间偏移的信号处理方法,在轴承故障特征提取领域得到了广泛的应用。

ZHAO M等人[5]使用一种新颖的奇异值分解方法,对轴承故障信号进行了截断降噪,取得了较好的效果,但该研究并未关注信号的细节特征。崔伟成等人[6]使用拟合误差最小化原则,对奇异值分解的截断阈值进行了选择,其重构信号的信噪比得到了大幅度提高;但其重构信号仅能提取4阶倍频。黄晨光等人[7]使用了一种新的差分奇异值比谱,并成功地提取到了轮对轴承的故障特征;但是该方法也存在细节特征提取不完全的问题。

此类通过选定奇异值截断阈值以获得较好信噪比的重构信号的算法,被统称为截断奇异值分解(truncatedsingular value decomposition,T-SVD)。

吕靖香等人[8]在相关的研究中指出,T-SVD必然带来局部特征的失真和细节信息的丢失,但是该研究并未对此进行深入探讨。

因此,现有的分解重构算法固然可以有效分离原始信号和噪声信号,但其往往会导致局部信息和细节特征的丢失。

由于旋转机械和轴承的结构特性,轴承的动态响应具有循环平稳特性。循环平稳过程是一种统计量具有周期性的特殊随机过程,这种性质为人们使用瞬态重复的方式描述故障统计特征提供了可能。

KRAVETS I[9]将谱相关(spectral correlation,SC)分析作为循环平稳分析法的一种有效方法,通过增强信号中的周期成分,以达到分离周期信号与噪声信号的目的,但其并未对此进行深入研究。CAPDESSUS C等人[10]将SC作为齿轮故障诊断的分析方法,取得了较好的效果,但是SC方法涉及的随机过程的理论复杂性以及计算冗余制约了其继续向纵深方向发展。ANTONI J等人[11]提出了循环调制谱(cyclic modulation spectrum,CMS)以代替SC的方法,提高了其运算的速度;但是CMS不是SC的无偏估计,因此其计算精度和频率分辨率难以满足实际需要。ANTONI J等人[12]提出了快速谱相关(fast spectral correlation,FSC)算法,同时改进了SC算法计算速度慢和CMS算法精度、分辨率差的问题;但是作者并未讨论其噪声影响的问题。王兴龙等人[13]使用EMD与快速谱相关算法,对滚动轴承的故障特征进行了提取,但其并未对其中的算法进行深入研究。

在实践中可以发现,FSC包络增强强度和分辨率与信号采样长度密切相关,信号的随机成分导致FSC的降噪效果下降迅速。在实际使用时,用于传输大量数据的通信信道中的可用带宽是有限的。因此,在较低采样长度下,对故障进行有效的特征提取有助于减少通信和存储中的数据量,为该算法的在线检测使用提供便利。

综上所述,现有的滤噪算法无法在较好的信噪比与完整的细节特征之间取得平衡,FSC算法的循环增强效果受随机噪声影响巨大。

因此,笔者拟通过研究奇异值分解子信号空间的关系,提出能够更好保持信号细节特征的周期优选奇异值分解(O-SVD)算法;同时将其作为FSC的前置处理单元,以提高FSC输入信号的信噪比和确定信号的比重,通过仿真、实验数据以及实验台架,在早期微弱故障、复合故障和综合故障等3种情况下,将该算法与现有算法进行对比。

1 方法原理

1.1 奇异值分解原理

奇异值分解是指:设从振动传感器采集滚动轴承故障信号x(t)离散化后为x(l)=[x1,x2,…,xl],使用Hankel矩阵算子相空间重构轨迹矩阵X:

Xi=[xi,xi+λ,…,xi+(m-1)λ]T
X=[X1,X2,…Xn]

(1)

式中:λ—延迟时间;m—嵌入维数。

对于轨迹矩阵X∈Rm×m,无论其行列是否相关,必定存在正交矩阵U和V，使下式成立：

(2)

式中:S—矩阵Y的奇异值对角阵;Ai—矩阵X的i阶子空间。

在使用T-SVD进行降噪时,式(2)可转化为:

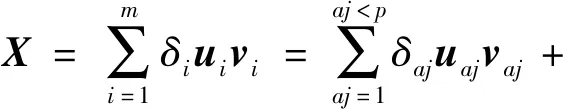
(3)

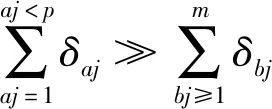
对Xa进行相空间反重构,可得到降噪后的近似信号xc(t)。

1.2 优选奇异值分解理论

已有的研究指出,x(t)进行奇异值分解后,当使用反对角重构法进行反重构时,相邻子空间重构信号具有相似关系,但该研究并未深入进行下去。

笔者通过理论和仿真研究深入证明了相关结论,现将仿真证明展示如下:

相关系数代表两个信号的相似程度,仿真证明以皮尔逊相关系数(pearson correlation coefficient,PC)为指标,探讨相邻子空间重构信号xci的关系。

基于早期伪平稳循环动态响应,可以建立如下模型:

(4)

其中:

(5)

式中:aj—第j个故障冲击的幅值;g—轴承的衰减系数;M—轴承冲击激发的个数;γ(t)—伪循环时间;T—轴承故障冲击的周期;τj—相对滑动引起的时间延迟;fe—故障特征频率。

仿真信号参数如表1所示。

表1仿真参数

早期伪平稳循环动态响应添加-8 dB噪声后,仿真信号时域波形如图1所示。

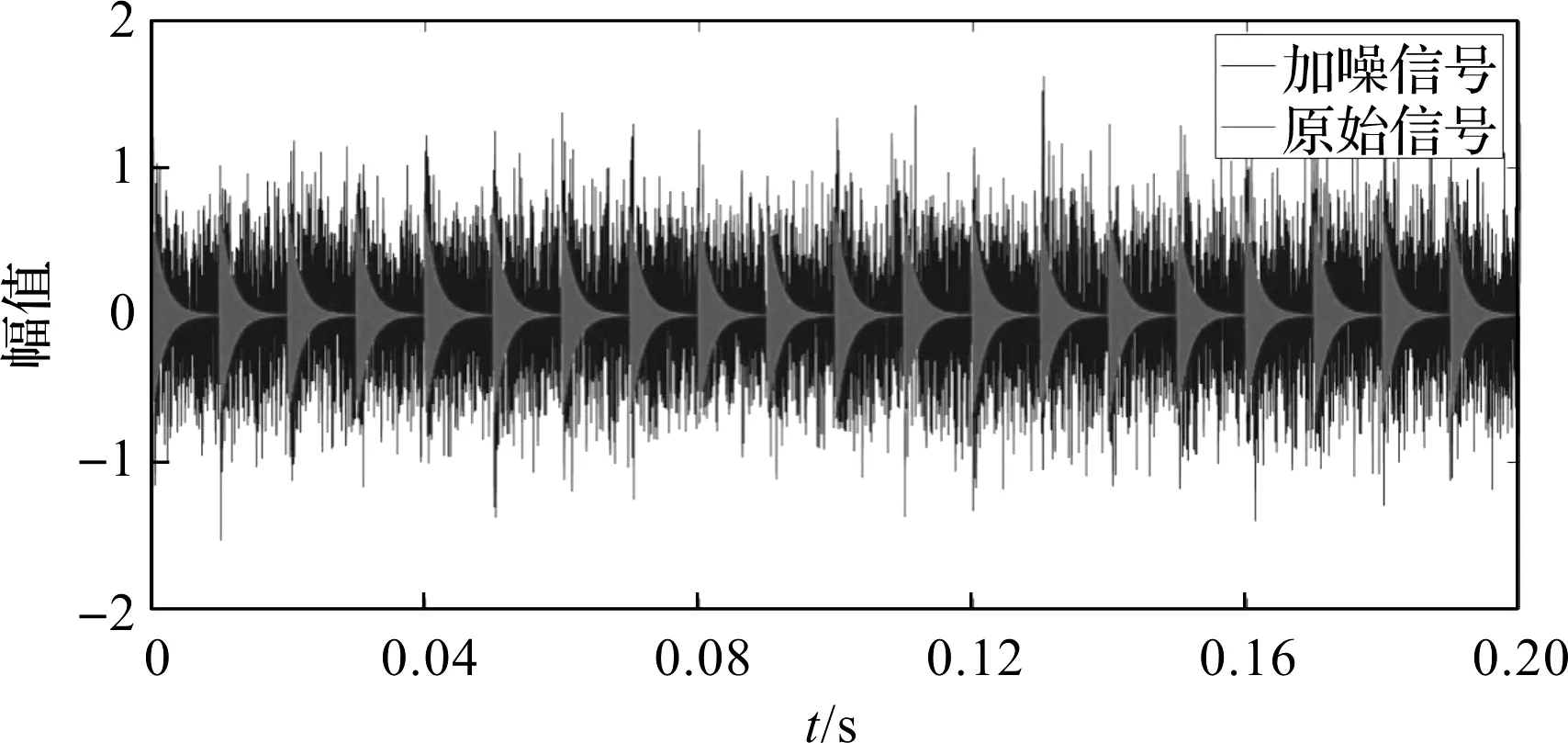
图1 仿真信号时域波形

通过计算假设信号相邻重构子信号的PC,SVD相关性仿真证明如图2所示。

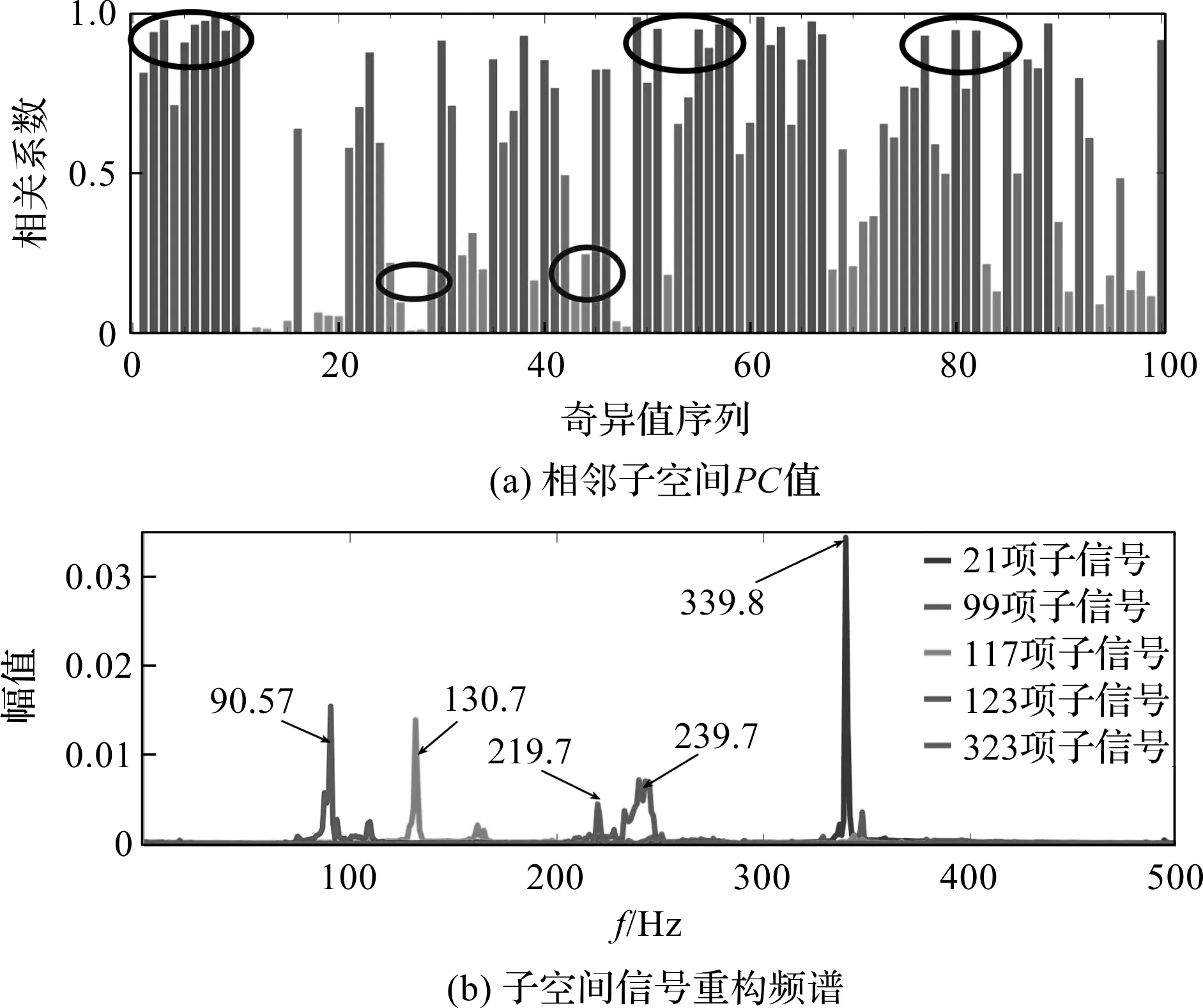
图2 SVD相关性仿真证明

图2(a)中,相邻向量的相关系数在某些阶次(如黑色圆圈)达到了高度相关(PC大于0.8),这些阶次的子空间矩阵包含了大量的有效信息;而其他阶次相邻向量的相关系数为低相关,这些阶次的子空间矩阵被噪声污染严重或包含周期信号较少。

为了进一步证明上述观点,笔者任选大于0.9的第10、49、58、61、166项相关序列,分别对第21、99、117、123、323项子信号序列进行了重构(相关系数代表奇异值序列2p和2p+1的相关系数),其频谱如图2(b)所示,子信号频率为特征频率10 Hz的倍数,为原信号的高阶本征固有模式。

通过仿真,证明了具有高相关系数的子空间信号表征周期信号,即通过计算子信号空间的相关性,能够优选出具有周期特性的有效信号。

1.3 周期优选奇异值分解

在优选奇异值分解的基础上,笔者提出了周期优选奇异值分解(O-SVD)算法,其具体表述如下:

(6)

式中:P—周期优选奇异值分解的阶次取值矩阵,P可通过计算相邻阶次奇异值分解的PC值得到。

其具体可表述为:

P=[1,2,…,2j-1,2J,…]

(7)

其中:

(8)

式中:pci—相邻子空间信号的相关函数。

1.4 快速谱相关算法

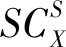
(9)

式中:Fs—采样频率;tn—等时间采样时间的间隔;RX(tn,τm)—循环自相关函数;τm—时滞因子;α—循环频率;f—信号频率。

定义快速谱循环为:

(10)

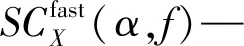
定义基于FSC相关函数:

(11)

并定义基于快速谱的增强包络谱:

(12)

经过计算可知,FSC最小分辨率(Δα)fast与计算消耗时间Tfast分别为:

(13)

式(13)中,最小分辨率与采样长度呈反相关,消耗时间与采样长度呈正相关。因此,在采样长度较少的情况下,保证算法分辨率能够检验算法提取微弱故障特征的能力,而且对于算法实现在线监测也具有重要意义。

2 基于O-SVD与FSC的算法步骤

笔者所提算法,即级联O-SVD与FSC算法步骤如下:

(1)确定嵌入维数m和延迟时间λ,对采集信号x(t)进行相空间重构,获得其轨迹矩阵X;

(2)利用SVD对轨迹矩阵进行分解,并使用反对角重构算法获得各阶次子空间反重构信号xc;

(3)计算相邻阶次子空间反重构信号的PC值pci,根据阈值τ确定周期优选奇异值分解的阶次取值矩阵P;

(4)计算O-SVD的修正软阈值系数ρi。获得重构矩阵Xc,并利用反重构算法获得降噪信号xc(t);

(5)将xc(t)通过FSC进行谱相关计算,获得其增强包络谱以进行故障诊断。

3 仿真分析

在强背景干扰情况下,为了验证该算法提取微弱特征的有效性,笔者构建了滚动轴承伪平稳循环动态响应数学模型,即:

(14)

式中:x(t)—早期伪平稳循环动态响应,取值如表1;δ(t)—单幅值冲击信号;n(t)—高斯白噪声。

在信噪比为-8 dB,采样长度L=6 000情况下,笔者分别采用直接FSC算法、T-SVD+FSC的分析结果、基于O-SVD与FSC的算法进行分析,并对各自的分析结果进行了对比。

采用3种算法的增强包络谱如图3所示。

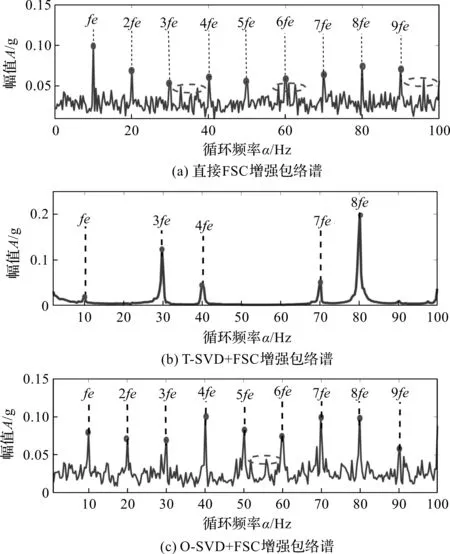
图3 3种算法增强包络谱

图3(a)为采用直接FSC的分析结果,增强包络谱信噪比较差,在3、4、6倍频处甚至出现了噪声信号与特征信号幅值相同的情况,难以准确识别故障特征;

图3(b)为采用T-SVD算法的分析结果,其噪声抑制效果极好,但是能够明显辨别的仅有3、4、7、8倍频谱线,fe基频幅值很小难以准确辨别,大量特征和细节信息丢失,对判定故障特征频率产生较大阻碍;

图3(c)为采用基于O-SVD与FSC的算法的分析结果,其噪声的抑制效果较好。通过增强包络谱可以清楚辨别9阶倍频谱线,能够明确辨别故障特征。

为定量分析算法对于故障信号的提取和增强性能,笔者根据文献[14],定义ρP为P算法轴承故障识别率,其表述如下:

(15)

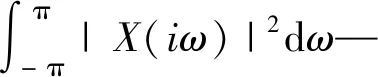
笔者定义β(P,Q)为P、Q两种算法对故障的识别熵:

(16)

式中:ρP—O-SVD+FSC算法的故障识别率;ρQ—直接FSC算法的故障识别率。

采用两种算法得到的识别率对比结果如图4所示。

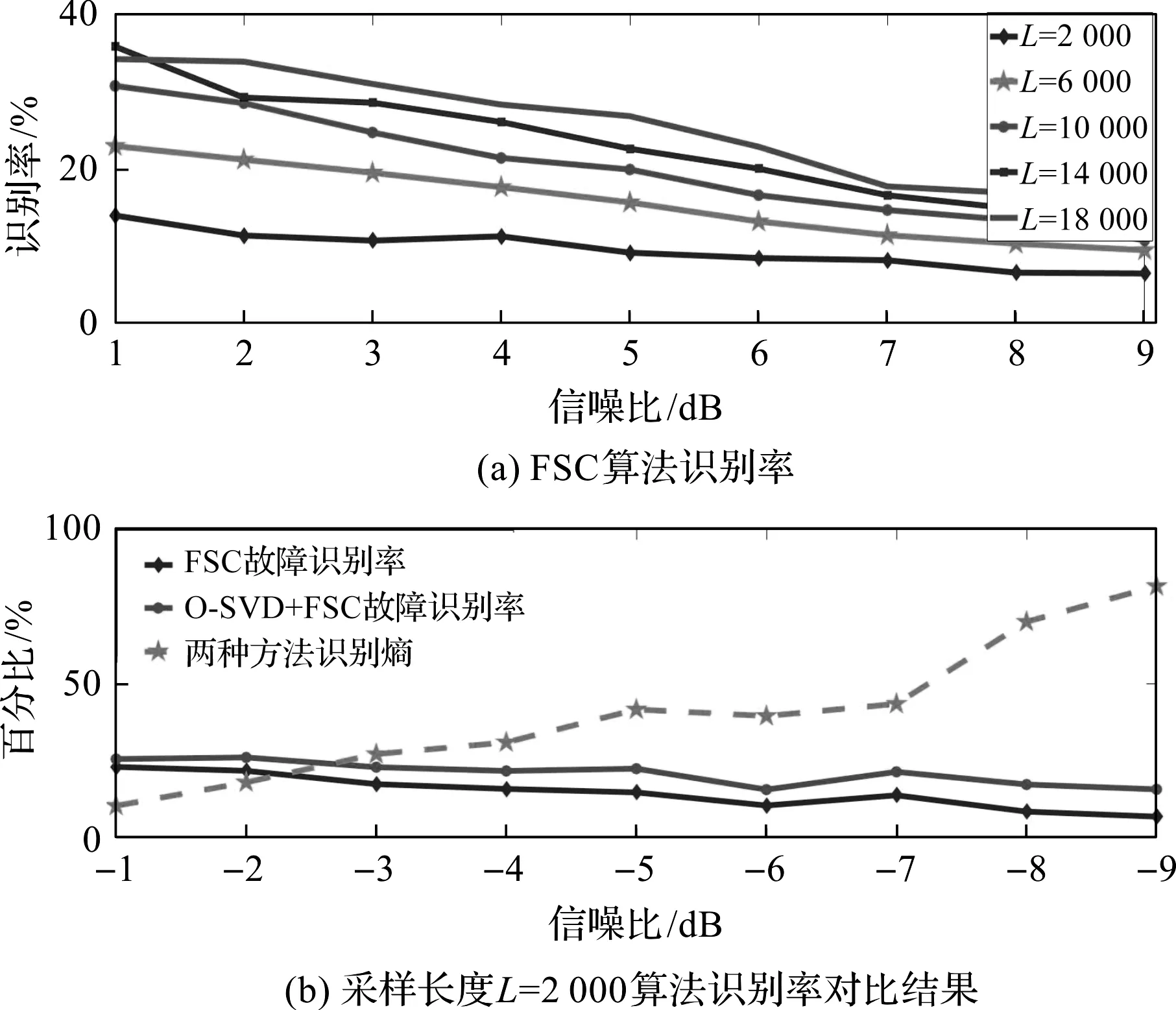
图4 两种算法识别率对比结果

图4(a)中,信号的采样长度对识别率有促进作用,信噪比对识别率影响巨大。因此,在较少采样长度情况下,对轴承的故障特征的完整提取更能够证明算法的优越性以及实际适用性;

图4(b)中,基于O-SVD与FSC的算法对信噪比变化的鲁棒性较高,在低信噪比情况下具有更好的工程适用性。

4 实验验证

4.1 早期故障实验数据验证

西安交通大学雷亚国教授团队提供的轴承加速全寿命周期数据[15],丰富了故障诊断和性能退化研究实验数据。该试验中的轴承为LDK UER204滚动轴承。

笔者使用该数据初期故障时间的实验数据,以验证基于O-SVD与FSC的算法对单一故障和复合故障的早期微弱特征的分辨能力,并将采用EEMD、FSC级联算法与基于O-SVD与FSC的算法得到的分析结果进行对比。

在信号采样长度L=4 800情况下,采用两种算法得到的单一故障信号增强包络谱如图5所示。

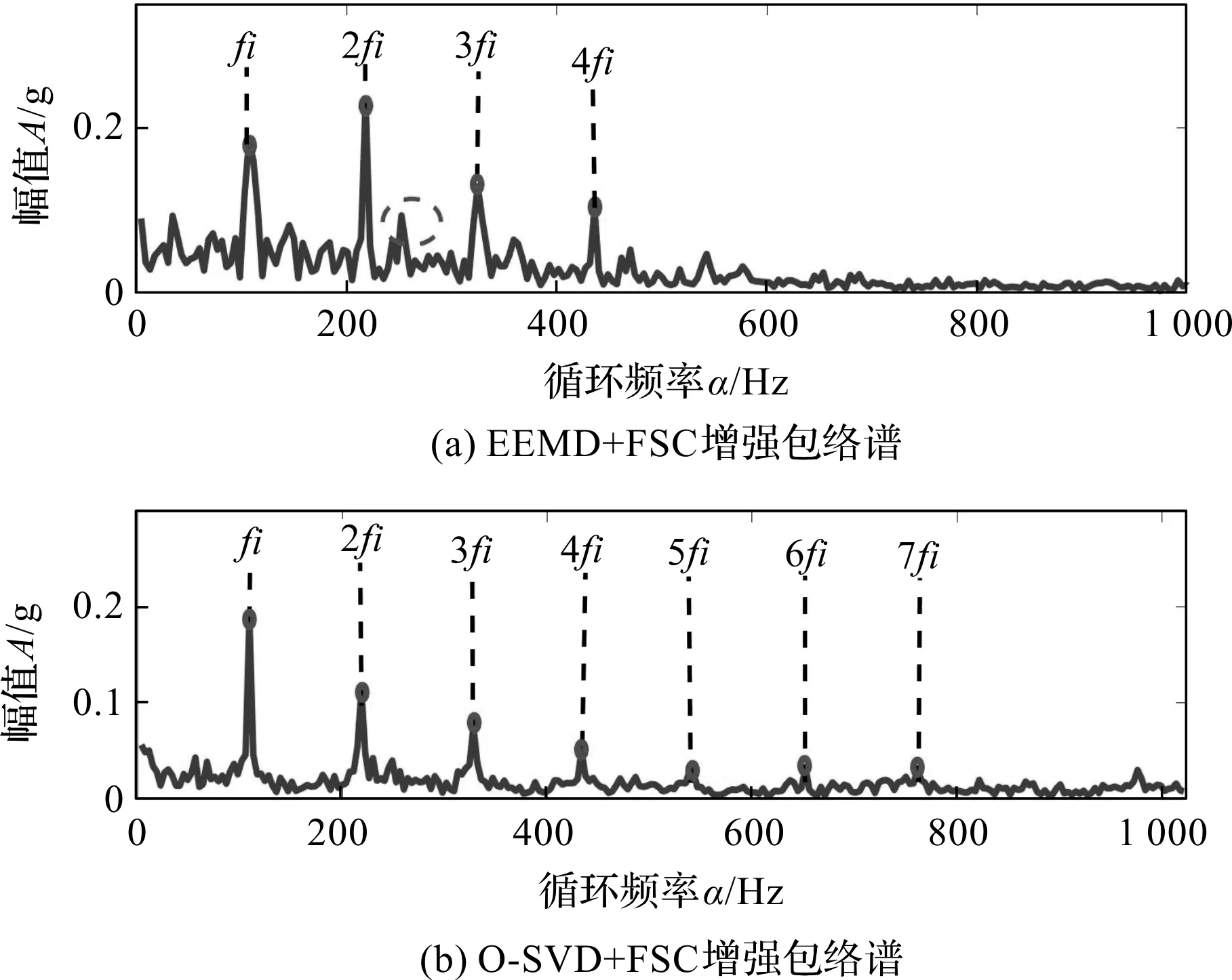
图5 两种算法初期微弱故障信号增强包络谱

图5中,EEMD+FSC增强包络谱信噪比较低,识别的倍频数较少,而基于O-SVD与FSC的算法能够较好地识别故障特征。

由于多种故障的耦合作用,会使其故障频率相互干扰,因此,复合故障的早期故障特征的提取难度更大。

在采样长度L=6 400的情况下,采用两种算法得到的复合故障信号增强包络谱如图6所示。

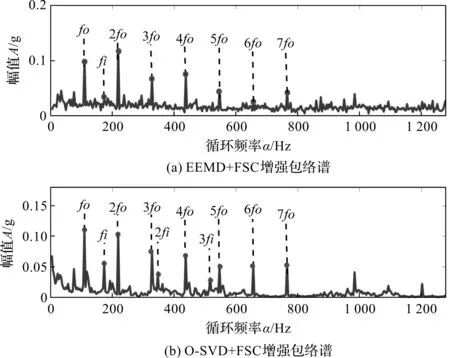
图6 两种算法复合故障信号增强包络谱

图6中,当笔者采用EEMD+FSC算法进行提取时,由于复合故障的耦合导致的频域间的干扰,算法增强包络谱丢失了在垂直布置传感器采集到的较为微弱的内圈故障,仅能较好分辨外圈故障;而采用基于O-SVD与FSC的算法提取的复合故障特征较好,两种故障特征均能够得到较好的分辨。

4.2 台架实验验证

此处台架实验采用SpectraQuest的旋转机械故障试验台,故障轴承型号MB ER-12 K,设置包含滚珠故障、内圈故障、外圈故障和保持架故障等类型的综合故障。

转速保持恒定在2 700 r/min,使用LMS SCADAS移动数据采集系统采集加速度传感器的振动信号,采样频率为25.6 kHz。

计算各故障特征频率如表2所示。

表2 特征频率

实验布局如图7所示。

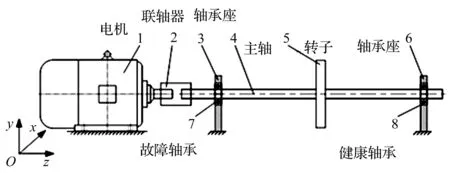
图7 实验布局

由于多种故障的耦合作用,使其故障频率相互干扰,综合故障信号的特征提取难度更大。

在采样长度L=9 600的情况下,采用直接FSC算法和基于O-SVD与FSC的算法得到的综合故障分析结果如图8所示。

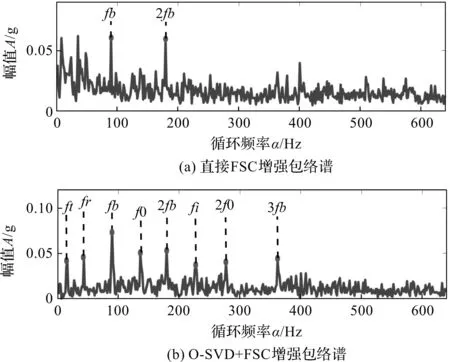
图8 两种算法综合故障信号增强包络谱

图8中,与直接FSC相比,采用基于O-SVD与FSC的算法能够较好地显示包含保持架、滚动体、外圈和内圈的轴承综合故障特征信息。

但是需要特别指出的是,伴随着故障特征的增加,故障频率干扰情况加重,需要采用更多的数据进行包络增强。

5 结束语

在低信噪比工况下,滚动轴承的早期微弱故障特征难以被完整地提取出来,针对这一问题,笔者提出了一种基于周期优选奇异值分解(O-SVD)和快速谱相关(FSC)的滚动轴承微弱故障提取算法,并进行了仿真和实验数据验证。

研究结论如下:

(1)在非线性、高噪声工况下,采用传统的T-SVD降噪算法会产生细节特征丢失的问题,如果以相邻空间子信号PC为指标,则可以优选出表征周期信号的子空间阶次;

(2)FSC算法的包络增强性和故障分辨率与采样长度密切相关;仿真结果表明,与对比算法相比,笔者算法能够更加完整地提取出信号的细节特征;

(3)实验结果表明,与EEMD+FSC算法相比,在发现早期故障、保证提取特征完整性方面,笔者算法的优势明显;台架实验结果证明,与直接FSC算法相比,笔者算法提取的综合故障信号特征具有滤噪效果好、提取特征完整的优点。

在当前的研究中,笔者仅仅关注了冲击性故障的特征提取,而对于平稳性故障的特征提取研究尚未展开。因此,在后续的工作中,笔者将展开对平稳性故障特征提取的研究工作。