机床导轨爬行问题的双质体模型的仿真分析*

周 阳,兴成浩,赵娴旻,马紫音,房 毅*

(1.华东理工大学 物理学院,上海 200237;2.华东理工大学 机械与动力工程学院,上海 200237)

0 引 言

机械工程中的爬行是指机床进给系统各部件在恒定传动和一定摩擦力的条件下,不以恒定速度连续运动,而是时走时停或时快时慢的现象。

爬行是机床中常见的有危害的现象,会大大影响导轨运作的均匀性,减少定位精度和灵敏度,进而严重影响工件表面的加工精度和表面粗糙度;同时还会造成机床导轨的加速磨损,甚至导致加工零件直接报废。

要提高机床加工精度与品质,势必要解决机床爬行问题。因此,这已成为提高机床加工精度与品质的重要研究课题,是改进精密和超精密仪器的重要研究方向之一。

爬行问题最早是在20世纪30年代被提出的。国外物理学家对爬行产生的原因进行了讨论,但没有细致地分析不同因素对爬行的具体影响。其中,BANERJEE A K[1]认为爬行是一种摩擦自激振动现象。BOWDEN F P等人[2]认为爬行是由两金属表面的真实接触点互相焊合导致的。MOKHTAR M O A等人[3]认为爬行是由滑动过程中静、动摩擦因数的不同及摩擦力变化导致的。

国内学者对爬行的研究从20世纪70年代开始,吴圣庄[4]研究了爬行产生的原因,并提出了一些防爬措施,但并未建立具体的爬行模型,也没有对爬行的影响因素进行细致分析。还有许多学者都将机床进给系统爬行的机理简化成了摩擦振子运动模型并加以分析。如张文俊[5]38针对中世纪星型数控车床建立了简化的单质体单自由度模型,研究了其低速运行时产生的爬行现象,但低速的限制条件使得探究的影响因素不够全面,且单质体单自由度模型比较简单。龚庆寿[6]也建立了单质体单自由度模型,研究了机床进给系统中产生爬行现象的自激振动机理,但这样的单质体单自由度模型太过简单,与实际不是很贴合。而卢泽生等人[7]研究了单质体两自由度模型产生的爬行现象,实现了一种突破,但与机床工作的实际情况更为贴近的是双质体(乃至多质体)、两自由度(乃至多自由度)的模型。

笔者选用双质体爬行物理模型,通过ADAMS进行建模仿真,遵循控制变量的原则进行探究,对仿真获得的结果进行数据处理,选择合适的爬行评价指标,进而对影响爬行的因素进行探究分析。

1 爬行机理

1.1 物理模型

笔者选用的双质体爬行物理模型[8]如图1所示。

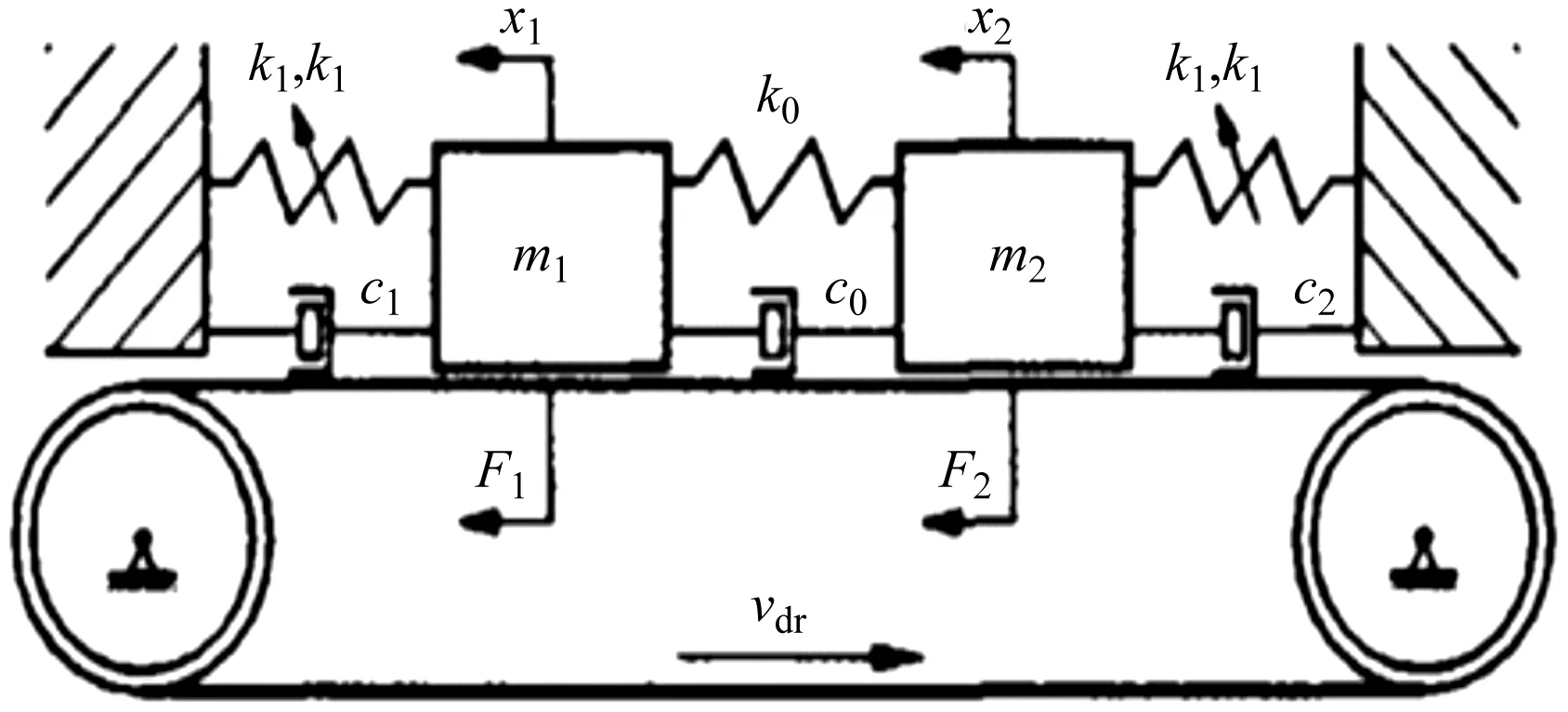
图1 双质体爬行物理模型vdr—传输带作单向运动的速度;m1,m2—两个质体的质量;F1,F2—产生的摩擦力;x1,x2—两个质体的位移;ki—刚度系数;ci—阻尼系数

1.2 数学模型

根据图1所示的双质体物理模型,可以得到系统的运动微分方程为:

(1)

干摩擦力F1、F2采用Stribeck模型。在Stribeck模型中,干摩擦力F满足:

(2)

式中:vr—界面相对滑动速度;μs—静摩擦因数;N—界面间压力。

其中:

(3)

(4)

式中:μm—最小动摩擦因数;vm—最小动摩擦因数对应的速度值。

观察物理模型及得到的运动微分方程可知,爬行过程中的状态参数与系统的质量、阻尼系数、弹簧刚度、驱动速度、动摩擦因数与静摩擦因数之差有关。

2 ADAMS爬行仿真模型的建立

ADAMS,即机械系统动力学自动分析软件,该软件是美国机械动力公司(Mechanical Dynamics Inc.,现已并入美国MSC公司)开发的虚拟样机分析软件,利用ADAMS建模便于进行多体动力学仿真[9]。

笔者利用ADAMS进行了建模,ADAMS所建模型如图2所示。

图2 ADAMS所建模型

在模型中,两个质体中间以及质体和两侧固定壁面之间各自有一个弹簧,物块下面是一个传动速度保持不变的传送带,在ADAMS中,将其简化为一个无限大的匀速运动的平板,最终的效果与传送带相同。

整个研究过程遵循控制变量法的原则,并且通过改变一系列的参数,如动摩擦因数、静摩擦因数、物体质量、弹簧刚度和阻尼等,把得到的数据输入Origin分析软件中,最终可以获得质体的位移、速度、加速度以及反作用力随时间变化的规律曲线。研究人员通过曲线峰值和它的变化趋势判断是否出现爬行现象,并对其进行进一步的分析。

3 仿真结果分析

3.1 爬行评价指标

为评价爬行,需选择爬行评价指标。现有的对爬行的研究针对的多为时走时停的爬行现象,采用最大爬行步、位移波动量、速度波动量、纹波率、停留时间等评价指标[10]。而笔者研究的双质体模型产生的是时快时慢的爬行现象,从位移时间曲线中很难辨别出前后两次位移变化速度放缓之间的爬坡量。因此,诸如最大爬行步这样与位移相关的爬行评价指标不再适用。

笔者选择了3种爬行评价指标,分别为速度波动量(ΔV)、最大速度误差(dVmax)[11]16和纹波率(δV)。速度波动量是运动部件呈近似稳定运动后最大速度与最小速度的差值。最大速度误差是运动部件呈近似稳定运动后实际速度与理想速度间最大偏差的绝对值。纹波率是速度波动量与最大瞬时速度的比值。

3.2 仿真实验结果分析

3.2.1 质量对爬行的影响

物体质量会影响爬行现象的剧烈程度[11]19。为了探索质量与爬行程度的关系,笔者将物体分别设置成5个质量大小进行动力学仿真实验。5个质量分别为:1 kg、100 kg、200 kg、300 kg、600 kg。其中,取质量为1 kg这一比较极端的值是为了在曲线图中能更清楚地辨析质量对爬行的影响。

笔者设置固定参数如表1所示。

表1 仿真参数设置

通过处理仿真数据,笔者得到5个不同物体质量下的速度与时间关系曲线,如图3所示。

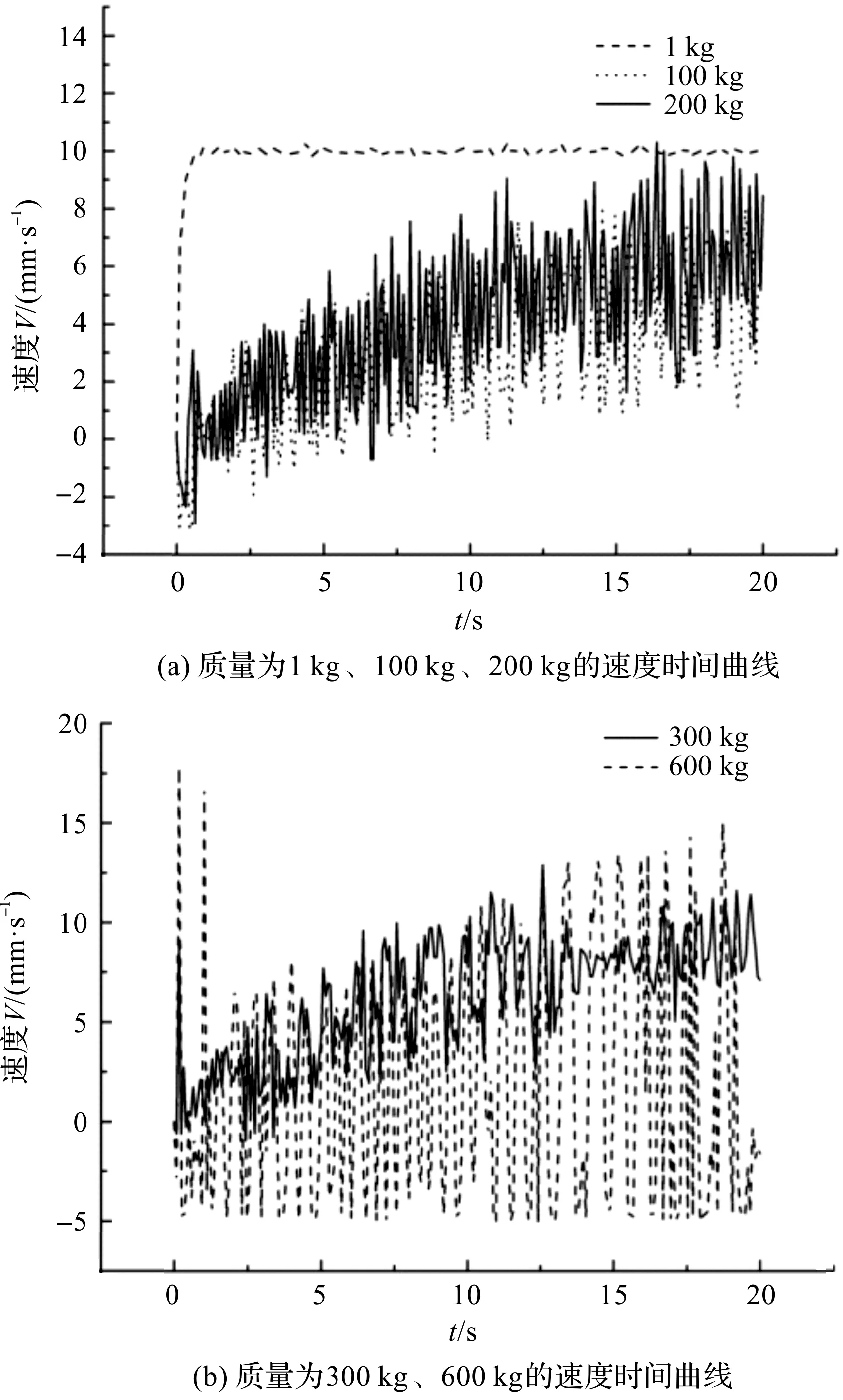
图3 不同质量下物体速度与时间关系曲线

观察图3可以发现,速度波动大体上有随物体质量的增加而增大的趋势。经计算,在物体质量为1 kg时,速度波动量为0.20 mm/s;物体质量为100 kg时,速度波动量为6.88 mm/s;物体质量为200 kg时,速度波动量为9.03 mm/s;物体质量为300 kg时,速度波动量为11.97 mm/s;物体质量为600 kg时,速度波动量为19.60 mm/s。

不同物体质量下的速度误差曲线如图4所示。

图4 不同质量下物体速度误差曲线

观察图4中的坐标,并计算其纹波率,可以得到:在物体质量为1 kg时,最大速度误差为0.32 mm/s,纹波率为0.019 8;物体质量为100 kg时,最大速度误差为4.90 mm/s,纹波率为0.876 4;物体质量为200 kg时,最大速度误差为5.89 mm/s,纹波率为0.886 2;物体质量为300 kg时,最大速度误差为6.03 mm/s,纹波率为0.929 1;物体质量为600 kg时,最大速度误差为22.16 mm/s,纹波率为1.308 7。因此,最大速度误差和纹波率均随物体质量的增大而增大。

综合评价结果可见,随着物体质量的增加,爬行的各项表征参数增大,可以得出降低系统的质量能抑制爬行的结论,为改善机械工程中的爬行现象提供了一种方法。

3.2.2 阻尼系数对爬行的影响

阻尼是使自由振动衰减的各种摩擦和其他的阻碍作用,阻尼系数也是影响爬行现象的重要因素[12]。笔者分别将阻尼系数设置为0.1,100,200,300,400进行仿真。其中,阻尼取0.1这一极端值也是为了更容易地辨析阻尼对爬行的影响。

笔者设置固定参数如表2所示。

表2 仿真参数设置

通过处理仿真数据,可得到不同阻尼系数下的速度时间曲线,如图5所示。

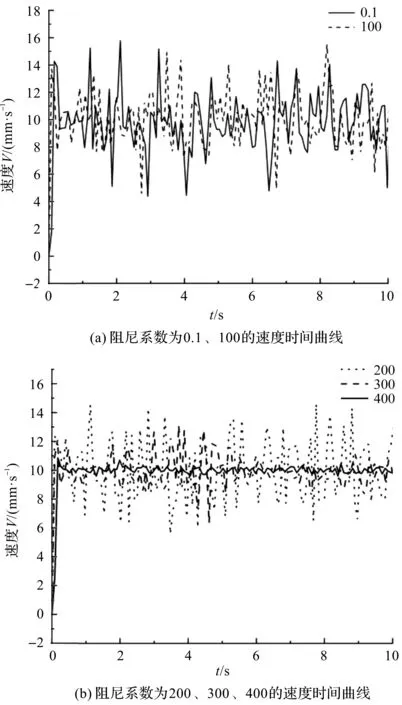
图5 不同阻尼系数下物体速度与时间关系曲线

观察图5,速度波动随阻尼系数的增加有所减缓。经计算,当阻尼系数为0.1时,速度波动量为11.35 mm/s;阻尼系数为100时,速度波动量为10.95 mm/s;阻尼系数为200时,速度波动量为8.90 mm/s;阻尼系数为300时,速度波动量为6.78 mm/s;阻尼系数为400时,速度波动量为1.07 mm/s。可见速度波动量随阻尼系数的增加的确有减小的趋势。

不同阻尼系数下的速度误差曲线如图6所示。

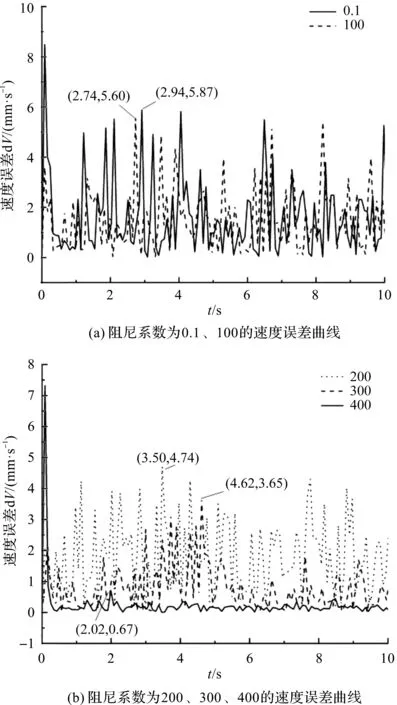
图6 不同阻尼系数下物体速度误差曲线

观察速度误差曲线并计算纹波率,可以得到:当阻尼系数为0.1时,最大速度误差为5.87 mm/s,纹波率为0.810 7;阻尼系数为100时,最大速度误差为5.60 mm/s,纹波率为0.733 1;阻尼系数为200时,最大速度误差为4.74 mm/s,纹波率为0.666 2;阻尼系数为300时,最大速度误差为3.65 mm/s,纹波率为0.482 3;阻尼系数为400时,最大速度误差为0.67 mm/s,纹波率为0.142 1。因此,系统的最大速度误差和纹波率都随阻尼系数的增加而减小。

对整体而言,系统的速度波动量、最大速度误差和纹波率均随阻尼系数的增加而减小,说明爬行程度随着阻尼系数的增加有所减小。可以采用增加阻尼系数的方法来抑制爬行。

3.2.3 弹簧刚度对爬行的影响

刚度越大,系统抵抗弹性变形的能力越高[11]20。笔者分别选取刚度值为1 N/mm,200 N/mm,500 N/mm,800 N/mm进行仿真实验。

相关固定参数的设置如表3所示。

表3 仿真参数设置

对仿真所得数据进行处理,可得到的不同刚度下的速度时间曲线,如图7所示。

图7 不同刚度下物体速度与时间关系

经计算,在刚度为1 N/mm时,速度波动量为11.07 mm/s;刚度为200 N/mm时,速度波动量为3.70 mm/s;刚度为500 N/mm时,速度波动量为12.13 mm/s;刚度为800 N/mm时,速度波动量为3.74 mm/s。笔者发现速度波动量随刚度的增加先减小、后增大、再减小,无明显的线性关系。

不同刚度下物体的速度误差曲线如图8所示。

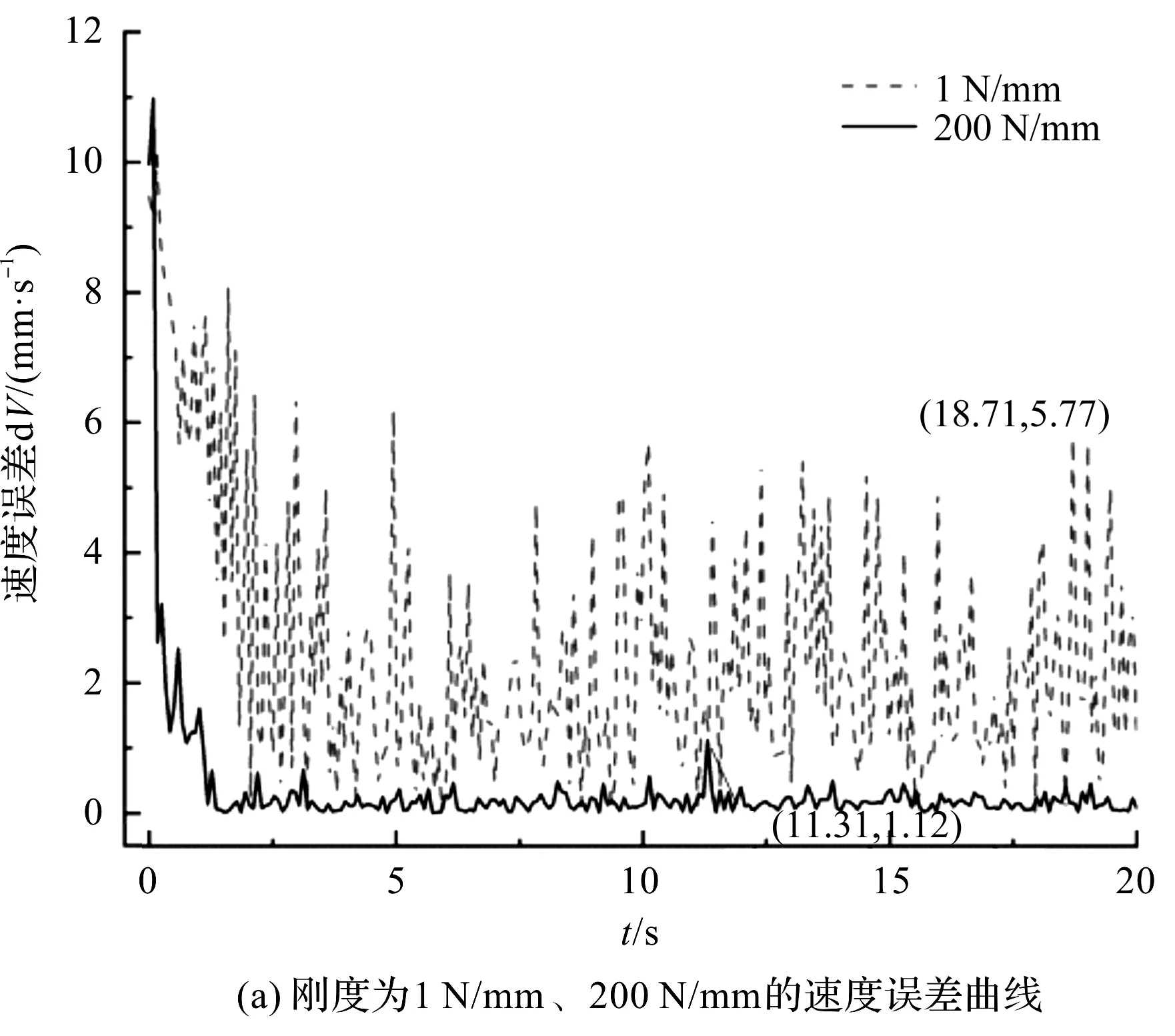
图8 不同刚度下物体速度误差曲线

图8中,观察所标坐标并计算纹波率,在刚度为1 N/mm时,最大速度误差为5.77 mm/s,纹波率为0.730 2;刚度为200 N/mm时,最大速度误差为1.12 mm/s,纹波率为0.356 6;刚度为500 N/mm时,最大速度误差为7.69 mm/s,纹波率为0.817 8;刚度为800 N/mm时,最大速度误差为2.42 mm/s,纹波率为0.369 1。

总的来说,速度波动量、最大速度误差和纹波率这3个指标均随刚度的增加而先减小,再增大,再减小。通过以上分析,可以发现爬行程度与刚度之间没有明显的线性关系,但存在最佳刚度值,使得爬行各项表征参数达到最小,从而使爬行现象得到明显抑制。

3.2.4 驱动速度对爬行的影响

驱动速度是影响进给系统出现时快时慢的爬行现象的一个重要因素。为了探究不同驱动速度对于爬行程度的影响,笔者分别设置4种驱动速度为10 mm/s、20 mm/s、30 mm/s、40 mm/s的系统进行仿真。

其固定参数设置如表4所示。

表4 仿真参数设置

通过对仿真获得的数据进行处理,可得到速度时间曲线如图9所示。

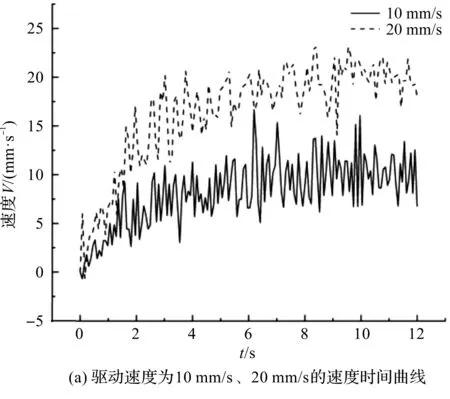
图9 不同驱动速度下物体速度与时间关系曲线

观察图9可以发现,速度波动随驱动速度的增加有减缓的趋势。经计算,驱动速度为10 mm/s时,速度波动量为11.61 mm/s;驱动速度为20 mm/s时,速度波动量为9.31 mm/s;驱动速度为30 mm/s时,速度波动量为3.46 mm/s;驱动速度为40 mm/s时,速度波动量为2.60 mm/s。

不同驱动速度下的速度误差曲线如图10所示。

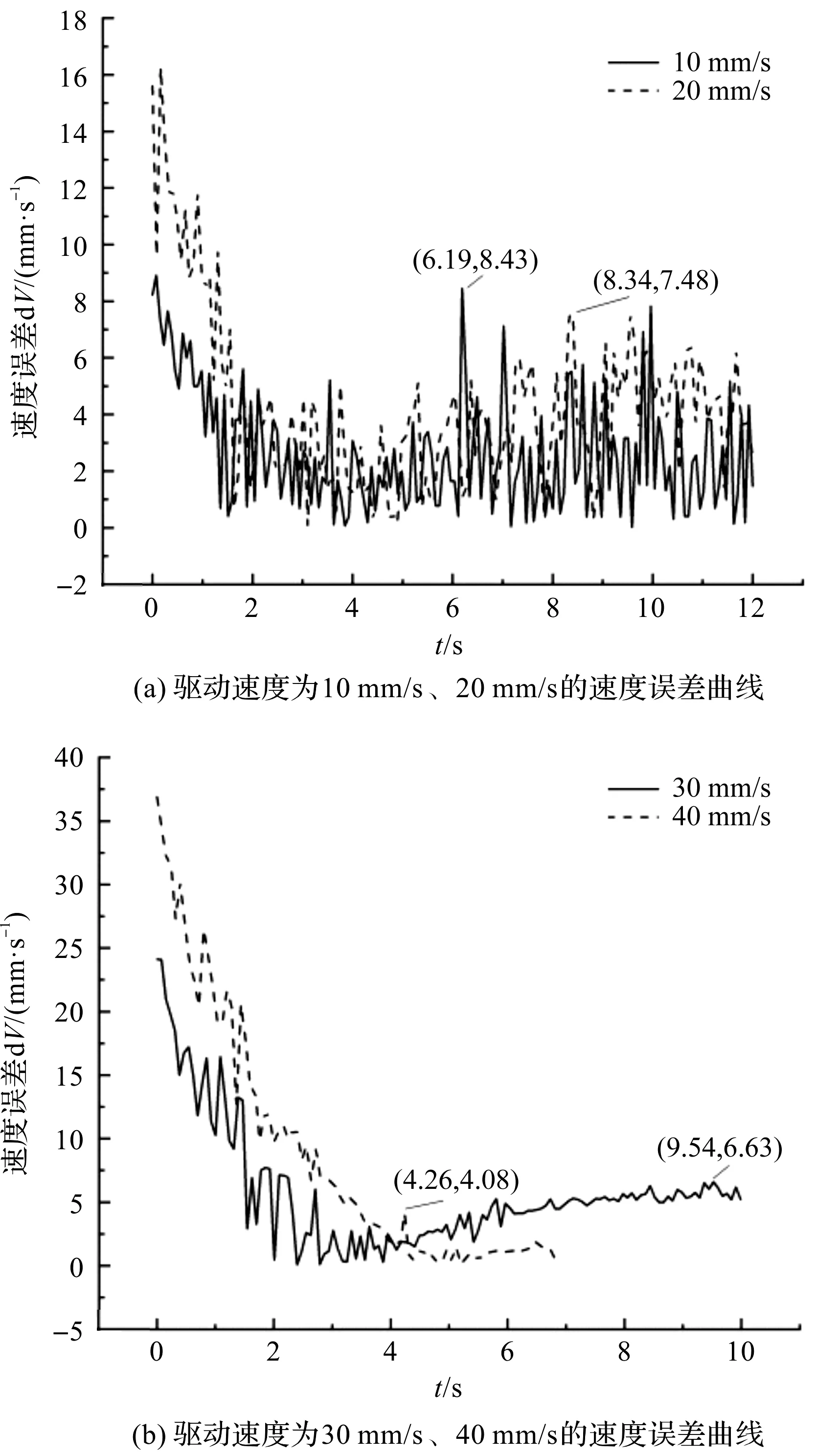
图10 不同驱动速度下物体速度误差曲线

图10中,观察所标坐标并计算纹波率,驱动速度为10 mm/s时,最大速度误差为8.43 mm/s,纹波率为0.965 5;驱动速度为20 mm/s时,最大速度误差为7.48 mm/s,纹波率为0.393 8;驱动速度为30 mm/s时,最大速度误差为6.63 mm/s,纹波率为0.081 2;驱动速度为40 mm/s时,最大速度误差为4.08 mm/s,纹波率为0.069 9。可见,伴随着驱动速度的增加,最大速度误差和纹波率都会有下降的趋势。

3个评价指标的变化都说明了爬行现象随着驱动速度的增加有所改善。但随着驱动速度的不断增大,上述评价指标的降幅也在不断减小。

因此,适当增加驱动速度可以较大程度地减小爬行。而当驱动速度增加到一定程度时,各评价指标变化较小,所以在实际工程应用中只要适当增加驱动速度就可以达到抑制爬行的目的。

3.2.5 动、静摩擦因数之差对爬行的影响

动、静摩擦因数之差是进给系统产生爬行的根本原因[11]21,因此,研究动、静摩擦因数之差对进给系统爬行的影响是探究如何抑制爬行的关键所在。笔者对机床进给系统进行动力学仿真,选取滑块与导轨之间动、静摩擦因数的差值分别为0.05、0.10、0.15、0.20。

固定参数如表5所示。

表5 仿真参数设置

通过对仿真结果进行数据处理,得到的速度时间曲线如图11所示。

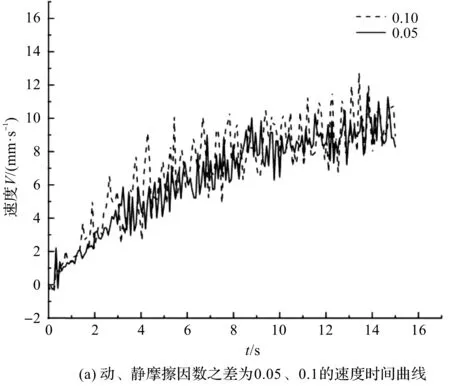
图11 不同动、静摩擦因数之差下物体速度与时间关系曲线

观察图11可以发现,速度波动量随动、静摩擦因数之差的增大而增大。经计算,在动、静摩擦因数之差为0.05时,速度波动量为5.74 mm/s;动、静摩擦因数之差为0.10时,速度波动量为7.44 mm/s;动、静摩擦因数之差为0.15时,速度波动量为9.98 mm/s;动、静摩擦因数之差为0.20时,速度波动量为12.68 mm/s。

不同动、静摩擦因数之差下的速度误差曲线如图12所示。

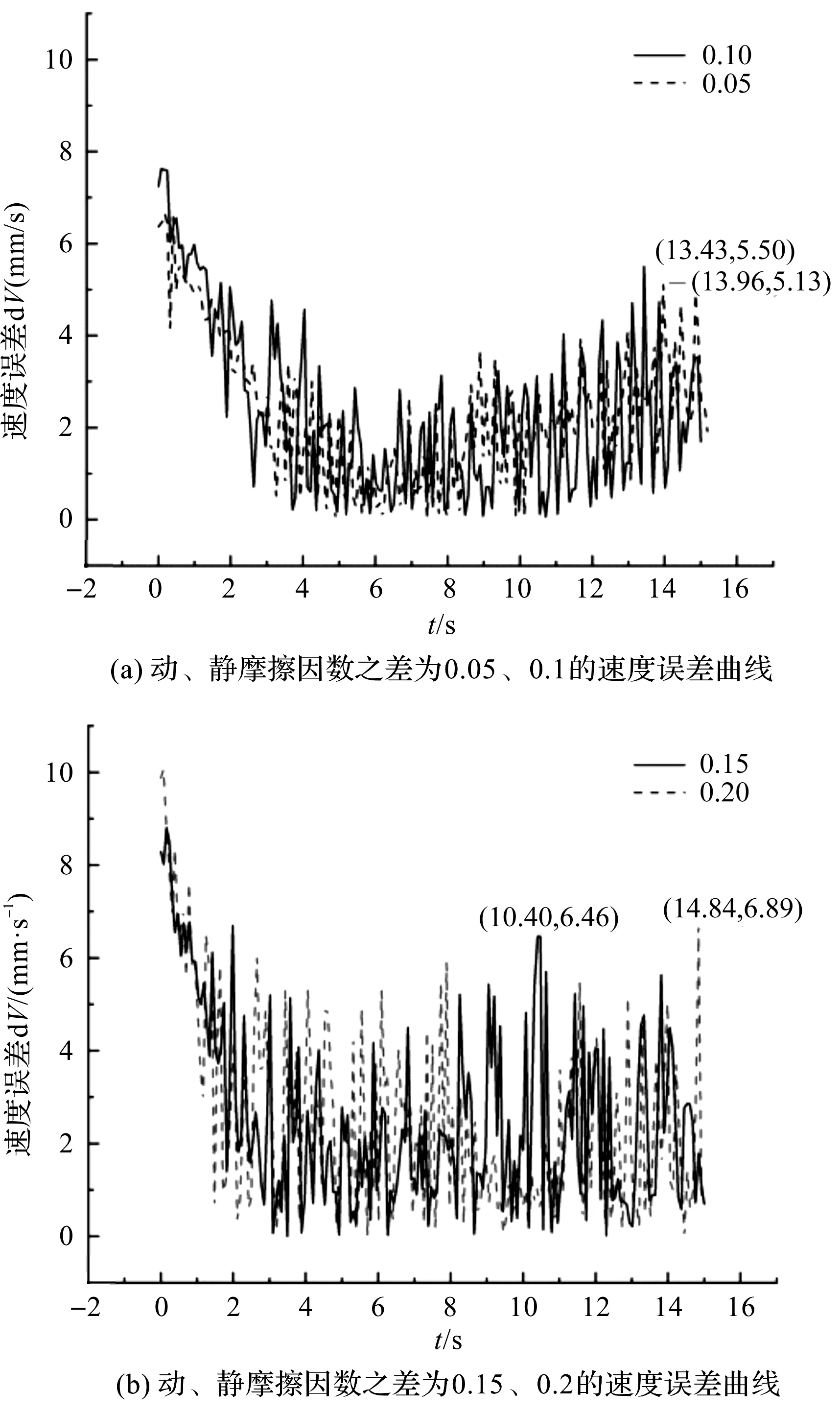
图12 不同动、静摩擦因数之差下物体速度误差曲线

观察图12的坐标,并计算纹波率可知,在动、静摩擦因数之差为0.05时,最大速度误差为5.13 mm/s,纹波率为0.546 2;动、静摩擦因数之差为0.10时,最大速度误差为5.50 mm/s,纹波率为0.615 1;动、静摩擦因数之差为0.15时,最大速度误差为6.46 mm/s,纹波率为0.676 7;动、静摩擦因数之差为0.20时,最大速度误差为6.89 mm/s,纹波率为0.767 5。

可以发现速度波动量、最大速度误差、纹波率都随动、静摩擦因数之差的增大而有所增大,且动、静摩擦因数之差与纹波率的关系几乎呈线性。由此可见,随着动、静摩擦因数之差的增大,爬行现象变得更加明显。故在工程上,减小动、静摩擦因数之差可以有效抑制爬行。

4 结束语

为了抑制机床导轨的爬行,提高机床加工的精度和品质,针对双质体爬行模型,笔者利用ADAMS对其进行了建模与仿真,分别分析了质量、阻尼系数、弹簧刚度、驱动速度、动摩擦因数与静摩擦因数之差等因素对机床导轨爬行的影响。

研究结果表明:

(1)降低系统的质量可以抑制爬行。实践表明,这样的方法是可行的。如可以通过减轻导轨面载荷抑制爬行[13];

(2)增加阻尼系数可以抑制爬行。实践中可以通过在丝杠—螺母副机构中用油脂包络螺母,或在导轨面间用高粘度润滑油来抑制爬行[14];

(3)选择最佳刚度值可以抑制爬行。该措施的可行性还有待验证;

(4)增加驱动速度可以抑制爬行。实践中,将“丝杠旋转型”滚珠丝杠换为“螺母旋转主驱动型”滚珠丝杠副,由伺服电机驱动,可以获得较为均匀的进给[15],可见通过增加驱动速度抑制爬行也是可行的;

(5)减小动、静摩擦因数之差可以抑制爬行。现代数控机床上广泛采用滚动导轨或气浮导轨,在进给传动系统中,大量采用滚珠丝杠螺母副或静压丝杠螺母副,这都是为了减小静、动摩擦因数之差,抑制爬行[5]39。

在后续的研究工作中,笔者可以对刚度对机床导轨爬行的影响进行探究,以选择其最佳的刚度值。